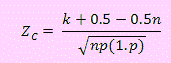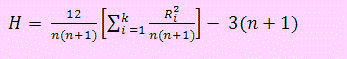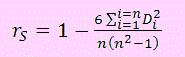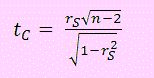CAPÍTULO 9

ESTADÍSTICA NO PARAMÉTRICA

9.1 Introducción
9.2 Prueba de signos
9.3 Prueba de rangos con signos de Wilcoxon
9.4 Prueba Mann – Witney – Wilcoxon
9.5 Prueba Kruskall – Wallis
9.6 Prueba de correlación por rangos de Spearman
9.7 Prueba de bondad de ajuste
9.8 Prueba de independencia de criterios
9.9 Prueba de homogeneidad de proporciones
9.10 Problemas propuestos

9.1 INTRODUCCIÓN

El uso que hemos hecho de la estadística ha sido para intentar explicar o comprender de alguna forma, el comportamiento de una población cuya distribución se define a partir de un conjunto de parámetros. Las muestras que hemos extraído y las herramientas utilizadas requieren de una serie de supuestos sobre la naturaleza de dichos parámetros. Por ello la estadística que hemos estudiado se la define como la Estadística Paramétrica.

Sin embargo, podemos realizar un análisis estadístico de un conjunto de datos cuya población de donde proceden es desconocida o simplemente no es paramétrica. Supongamos por ejemplo que se desea realizar un estudio sobre el número promedio alumnos que asisten a la universidad llevando consigo por lo menos un libro o el monto promedio de dinero en monedas con el que los alumnos asisten a la universidad . Naturalmente estas variables no provienen de poblaciones paramétricas.

Por otro lado, sólo el parámetro definido como la proporción de éxitos nos permite el estudio de datos ordinales. En este tipo de datos no podemos hablar de media, varianza, etc. Por estas dos razones estudiaremos algunos casos de la Estadística No Paramétrica.

Los métodos utilizados en la Estadística no paramétrica deben satisfacer alguno de los siguientes criterios:
i) Ser utilizado con datos nominales, aquellos que identifican, sea para conteo o identificación
ii) Ser utilizado con datos ordinales, aquellos que permiten ordenarlos tanto como valores discretos (codificados) o como categóricos, además de agruparlos porcentualmente.

iii) Ser utilizado con datos cuya unidad de medida sea de intervalo o de relación cuando no se formula ningún supuesto sobre la naturaleza de la existencia o forma de la distribución de probabilidad poblacional.

9.2 PRUEBA DE SIGNOS

Sea X₁, X₂,…, X_r un conjunto de r resultados obtenidos al aplicarle a una muestra algún criterio de tratamiento. Y sea Y₁, Y₂,…, Y_r los resultados obtenidos al aplicarle a la misma muestra un segundo criterio de tratamiento. Nuestro amigo lector estará encontrando similitud con el concepto de datos pareados. Sí, en efecto, este método también se puede aplicar a datos pareados y sin la exigencia de requerir la existencia o suposición de un parámetro. Más todavía, nuestro objetivo no consiste en evaluar la diferencia de valores como lo hace la técnica de datos pareados. Aquí queremos evaluar parejas de datos para manipular el signo de su diferencia: “*+” o “-“, para el cual, el único requisito es que ambas serie de resultados deban ser independientes.

Según esto, las hipótesis a plantearse son:
Ho: La proporción de signos “+” y signo “-“es la misma.
H1: La proporción de signos “+” y signos “-“no es la misma.

Procedimiento:

Colocar en una lista los pares de resultados obtenidos en pares de 1 a r

Para cada par, colocar a la derecha un signo “+” si el primero es mayor, un signo “-“ si el primero es menor y dejar en blanco si son iguales.

Sea p el número de signos positivos y m el número de signos negativos.
El tamaño de la muestra: n = p + m.
Sea k = Min{p,m}
Si X se define como el número de signos “+”. Como el número de éxitos es Binomial, hallar pValor = P(X ≤ k) = Distr.Binom(k,n,0.5,1)
Si pValor < α se deberá rechazar Ho; en caso contrario, no rechazarla.

Si el número de datos procesados es mayor a 25 (o 20), aplicando el teorema de aproximación de Binomial a Normal X-→N(0.5n ,np(1-p)) tal que



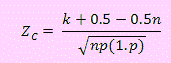
Criterio de decisión:
Si Z_C  > Z_α entonces se rechazará la hipótesis nula.

Nota:

Lo usual p = 0.5

Ejemplo 01

A un conjunto de personas presentes se les invitó a degustar un determinado tipo de queso. Luego de degustarlo se les pregustó si les parecía agradable o no, registrando “+” cuando la respuesta le parecía “agradable” y “-“ cuando manifestaba que no le era agradable y se dejaba en blanco en caso contrario.

Los datos están en la hoja PrbaSigno01 del archivo Estadística no paramétrica. Les resultó agradable a la mayoría de concurrentes? Use α = 0.05

Solución

Ho: No hubo diferencia significativa en la proporción de agrado o desagrado
H1: Sí hubo diferencia significativa en la proporción

Observando los cálculos, pValor = P(X ≤ k) = 0.407625

Como pValor no es menor a α no se rechaza Ho; es decir, no se puede afirmar que la proporción de concurrentes a quienes les agradó, sea mayor. Podríamos afirmar también que “a más personas les agradó el producto degustado”.

Ejemplo 02

En un laboratorio se desea probar una nueva técnica que debe reducir el tiempo para saber si un paciente tiene diabetes o no. Para ello se hicieron las pruebas usando la metodología antigua y se volvió aplicar la nueva técnica al mismo paciente. Esto se repitió con 17 pacientes. El tiempo se midió en minutos. Hay suficiente evidencia de que la nueva técnica reduce el tiempo para saber si el paciente tiene diabetes?

Solución

Los datos y la solución se encuentran en la hoja PrbaSigno02 del archivo mencionado en el Ejemplo 01.

PRUEBA DE RANGOS CON SIGNO DE WILCOXON

El test anterior nos permitió realizar comparaciones de pares de valores obtenidos en una muestra sobre los efectos que podría tener la aplicación de una acción sobre los mismos. Como se pudo comprobar, el método está basado en una distribución Binomial con p la probabilidad de éxito (tenga el signo +), siendo necesario que los elementos de la muestra fuesen independientes. Dijimos que cuando el tamaño de la muestra fuese grande, se podría usar el teorema de la aproximación de la Binomial a una normal. Finalmente en dicho test no estábamos interesados en tomar en cuenta el valor en cada pareja de datos, de allí la hipótesis nula que se formulara como que la proporción de éxitos (signos +) es la misma que la de fracasos (signos -). En cambio en un problema de datos pareados sí se requiere de la comparación de los valores en cada pareja.

En el presente test o prueba, seguiremos tomando en cuenta el signo o diferencia entre los pares pero también tomaremos en cuenta el valor de cada elemento en la pareja de datos. A partir de la diferencia entre ellos, los ordenaremos y le asignaremos un rango a cada diferencia, le asignaremos el signo que le corresponde a cada rango, obtendremos estadísticas de estos rangos y usando criterios aportados por Wilcoxon, estaremos en capacidad de rechazar o no la hipótesis nula.

Por ello es que el interés de esta prueba radica en tratar de probar la hipótesis de que la medida o acción aplicada a la muestra no presenta ningún efecto en uno u otro sentido; es decir, no hay diferencia significativa en la medida o acción aplicada a los elementos de la muestra.

Fundamento:

Sea X₁, X₂,…, X_r un conjunto de r resultados obtenidos al aplicarle a una muestra algún criterio o medida de tratamiento. Y sea Y₁, Y₂,…, Y_r los resultados obtenidos al aplicarle a la misma muestra un segundo criterio o medida de tratamiento.

Si definimos como T la variable resultante de éste método, entonces μ_T = 1/4 n(n+1)

σ²_T = 1/24 n(n+1)(2n+1)

Hipótesis:
En este caso la hipótesis nula consiste en afirmar que las poblaciones a la cual pertenecen ambos resultados es la misma o son idénticas. Esto es equivalente a formularlas de la siguiente manera:

Ho: El criterio aplicado no tiene efecto significativo en la muestra
H1: El criterio aplicado sí tiene efecto significativo en la muestra

Nivel de significación: 100α%

Procedimiento:

- Calcular Di = Xi – Yi
- Tomar el valor absoluto de ellas. De preferencia colocarlas en otra columna, acompañado de la identificación del número de elemento

- Ordenarlo de menor a mayor con la columna de identificación

- Asignarle un rango a cada elemento ordenado. Si un rango se repite k veces, el rango asignado a cada elemento que se repite será el promedio de los siguientes rangos. La siguiente diferencia tendrá por rango el número de rango que corresponda, si no hubiera habido repetición.

- Identificar el rango a cada diferencia original (sin el valor absoluto)

- Asignarle el signo positivo o negativo según el valor de la diferencia

- Sumar todos los valores de los rangos positivos y los negativos

- Elegir el mínimo de estas sumas. Este será el estadístico.

- Obtener el estadístico de la prueba usando: Z_C = (T-μ_T)/σ_T

- Si | ZC| > Z_α entonces se rechazará la hipótesis nula.

Ejemplo 03

En una clínica se aplicó un determinado medicamento a un conjunto de 8 pacientes usando el método A; se repitió el tratamiento pero usando el método B. Los resultados obtenidos se muestran en el siguiente cuadro. A un nivel de significación del 5% ¿se puede afirmar que es indiferente el método a usar?



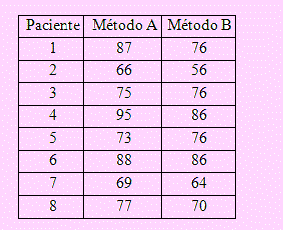
Solución



Ho: Ambos métodos proporcionan el mismo resultado
H1: Hay diferencia en la aplicación de los dos métodos.

El segmento de hoja anterior tiene todo el procedimiento y la solución del problema.

Explicación:

En la columna D hemos calculado las diferencias: =C2-B2
Hemos copiado la columna A (identificación del paciente) y el valor absoluto de la diferencia y los hemos pegado como valores en las columnas H e I.
Hemos ordenado estas dos columnas de menor a mayor.
En la columna J hemos asignado rango a estas diferencias absolutas ordenadas. Como no hay valores que se repiten los rangos se asignan como enteros secuenciales a cada rango.
Usando la función buscar hemos colocado los rangos en la columna E, para cada diferencia original.

 En la columna F le hemos asignado el signo que le corresponde a cada rango.
En F11 y F12 hemos sumado los rangos positivos y negativos. En F13 hemos hallado el mínimo de los valores absolutos de estas sumas. Ese es el estadístico T de la muestra.

En F14 hemos calculado el tamaño de la muestra que es el número de rangos positivos y negativos. En F15 y F16 hemos calculado la media y deviación estándar. En F17 tenemos el estadístico de la prueba y en F18 el valor crítico.

Finalmente, usando el criterio de decisión, no se rechaza Ho; es decir, ambos métodos proporcionan el mismo resultado.

Ejemplo 04

Una fábrica trata de determinar si dos métodos de producción tienen distintos tiempos de terminación del lote. Se seleccionó una muestra de 11 trabajadores y cada uno de ellos terminó el lote de producción con los dos métodos. Una diferencia positiva indica que el método 1 requirió más tiempo, en cambio si la diferencia es negativa, indicaría que el método 2 requirió más tiempo. ¿Indican estos datos que los dos métodos son significativamente diferentes? Los datos se encuentran en la hoja RangWil02 del archivo Estad no paramet.xlsx.

Solución

Las hipótesis a ser formuladas son:
Ho: Los dos métodos son iguales en el tiempo de terminación del lote
H1: Hay diferencia en el tiempo de terminación del lote por ambos métodos

El procedimiento es similar al descrito en el ejemplo anterior.

Luego de ingresar los datos, se obtiene la diferencia; se ordena tomando en cuenta las diferencias absolutas; se asigna un rango a cada diferencia absoluta; se le inserta el signo a cada rango según la diferencia original.

Se selecciona el mínimo entre ambas sumas, tomando sus valores absolutos; se calcula la media y desviación de T; se calcula el estadístico de la prueba y éste valor se compara con el valor crítico al 5% de nivel de significación.

Según apreciamos los resultados concluimos que se debe rechazar la hipótesis nula; es decir, podemos afirmar que los resultados obtenidos con los dos métodos es diferente y que el método 2 reduce el tiempo de terminación de producción del lote.

9.4 PRUEBA MANN - WITHNEY - WILCOXON

A diferencia del método anterior que se aplica a una sola muestra en dos comportamientos diferentes de la misma, en este método se comparan dos muestras independientes.
La diferencia que podemos encontrar con respecto a la diferencia de medias, resuelto en la estadística paramétrica son los supuestos a partir de la cual se comprobaron las hipótesis y éstos fueron:
- Las muestras aleatorias son independientes
- Las poblaciones de donde provienen son normales.
En este caso sólo se requiere del supuesto de que las muestras son independientes. Según esto las hipótesis a ser comprobadas a un nivel de significación del 100α% son:

Ho: Las muestras provienen de la misma población o las poblaciones son iguales
H1: Las muestras provienen de poblaciones diferentes.
Procedimiento

- Luego de disponer de las dos muestras, apilar los datos en una sola columna y en otra la forma de identificarlas. Sea n1 el tamaño de la primera muestra y n2 el tamaño de la segunda muestra.
- Ordenar las dos columnas de menor a mayor
- Asignar el rango a cada uno de los datos ordenados. Usando el mismo criterio de asignación: Cuando el dato se repite, se suman todas las repeticiones y se divide entre el número de datos repetidos, dicho resultado será el rango de todos ellos.
- El siguiente dato no repetido tendrá por rango el valor entero que le correspondería si no hubiera habido repeticiones.
- Se suman todos los valores de los rangos correspondientes a la misma muestra. Supongamos que estas sumas son S₁ y S₂, respectivamente.
- Se calculan los siguientes estadígrafos:



- Criterio de decisión: Si el valor absoluto de TC es mayor el valor crítico Zα, rechazaremos la hipótesis nula; es decir, las muestras no proviene de la misma población o las poblaciones de donde provienen no son iguales.

Ejemplo 05

La jefatura de atención al cliente de una empresa de servicio técnico vehicular, está preocupada en el rendimiento semanal de los obreros del turno diurno y nocturno en el sentido de que estos no tienen el mismo rendimiento. Para comprobar esta sospecha decide tomar una muestra del número de vehículos atendidos durante la semana por 22 obreros del turno diurno y 16 del turno nocturno. Los datos se encuentran en la hoja ManWitWill01 del archivo Estad. no paramétrica. ¿A un nivel de significación del 5% apoyaría Ud. la sospecha de la jefatura? ¿Cuál de los turnos tiene mejor rendimiento semanal?

Solución

Como puede apreciar, los datos se han ingresado en las dos primeras columnas.
Hemos apilado los datos en la columna D y el turno al que pertenecen cada dato, en la columna E.

Luego hemos ordenado por la columna D
En la columna F hemos asignado el rango a cada uno de los datos.
En L4 hemos calculado la suma de los rangos del turno diurno
En L5 hemos calculado la suma de los rangos del turno nocturno
En L11 se ha calculado el estadístico U₁, para el turno diurno y en L12 el estadístico U₂, para el turno nocturno.
En L14 hemos obtenido el mínimo de ellos que será el estadístico de la muestra.
En L17 tenemos el cálculo de la media y la varianza en L18.

Finalmente en L21 hemos calculado el estadístico de la prueba.
Luego de comparar su valor absoluto con el valor crítico decidimos rechazar la hipótesis nula.

Ejemplo 06

PetroSol es una empresa que tiene una cadena de estaciones de venta de gasolina de 84, 90 y 95 octanos. La gerencia de esta empresa ha decidido expandir su negocio añadiendo gasolina de mayor octanaje. Pero no han decidido si debe ser la de 97 octanos o la aditivada 98 octanos. Para tomar una decisión adecuada encarga a una empresa de mercado a fin de comparar el rendimiento por galón de ambos tipos de gasolina. Los datos se muestran en la hoja ManWitWill02 del archivo Estad. no paramétrica . A un nivel de significación del 5%, ¿podemos saber si hay diferencia significativa en el rendimiento por galón de los dos tipos de gasolina? Si así fuera, ¿cuál de los dos tipos aconsejaría Ud.?

Solución

La solución debidamente detallada y explicada se muestra en la misma hoja de los datos del archivo mencionado.

9.5 PRUEBA DE KRUSKALL - WALLIS

Esta prueba es similar a la prueba anterior, de Mann – Whitney – Wilcoxcon, excepto que se aplica para cuando el número de poblaciones es mayor que dos. El número de poblaciones cuyo comportamiento se desea analizar, la denotaremos por K. Se puede aplicar cuando se trata de variables ordinales así como también cuando se trata de variables de intervalo o de relación.

A diferencia de la prueba de K – medias en el cual se requiere que las muestras sean independientes y provenientes de poblaciones normales y que sólo es aplicable para variables de intervalo o de relación, en este caso sólo se requiere que las muestras sean independientes. Es ampliamente usado cuando los supuestos de normalidad y las varianzas no son conocidas.

La prueba consiste en probar la hipótesis nula de que las poblaciones desde donde se extrae las muestras son iguales o que no existe diferencia significativa entre estas poblaciones.

Para ello se procede como en la prueba anterior, a ordenar todos los datos de las k muestras siempre disponiendo de la forma de reconocer la pertenencia de los datos a su respectiva muestra. A continuación se debe asignar rangos a cada elemento. Se procede a sumar los rangos por muestra.

Sea R₁, R₂,…, R_k la suma de estos rangos. Sean también n₁, n₂,…, n_k los tamaños de cada una de las muestras, con n = n₁ + n₂ +… + n_k. A continuación se calcula el estadístico H usando


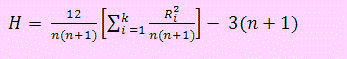
El atributo particular demostrado por Kruskall y Wallis es que este estadístico puede ser aproximado a una distribución χ²_1-α(k-1)

Criterio de decisión:
Si el estadístico H es mayor que χ²_1-α) (k-1) entonces se rechaza Ho en cuyo caso estaremos en capacidad de afirmar que sí existe diferencia significativa entre las k poblaciones o éstas no son iguales. La prueba también nos permitirá identificar la población que mejor se adapte a nuestro análisis.

Ejemplo 07

Un agente exportador de anchoveta está interesado en comercializar estos productos y colocarlos en mercados asiáticos. De acuerdo a la información que tiene, en el norte del Perú existen tres grandes empresas pesqueras bien constituidas de las que puede adquirir dichos productos pero no sabe si existirá diferencia significativa en los volúmenes de exportación mensual.
Para ello se registraron las ventas de los últimos meses de las tres empresas pesqueras, los que se muestran en el cuadro contenido en las primeras tres columnas de la hoja KruskWallis01 del archivo Estad. no paramétrica.
A un nivel de significación del 5%, ¿se puede afirmar que el agente puede adquirir dichos productos de cualquiera de las empresas pesqueras?

Solución

Las hipótesis que vamos a probar son:
Ho: Es lo mismo elegir cualquiera de las empresas (Las poblaciones son idénticas)
H1: No se puede a elegir cualquiera de ellas (Las poblaciones son idénticas)

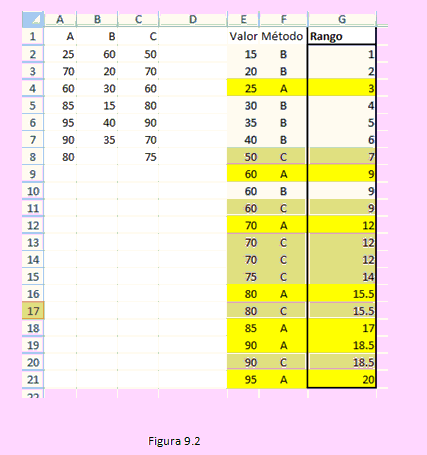
En la siguiente figura se muestran los datos y la primera parte del procedimiento.
En la columna G ya se han asignado el rango a cada uno de los datos.
En las celdas M4, M5, M6 y;M7, usando la función Contar.si() hemos obtenido los valores de n₁, n₂, n₃ y el tamaño de la muestra, n, como la suma de ellas.
En las celdas del rango R4:U6 hemos obtenido la suma de los rangos, su cuadrado y el cociente R_i/n_i.

En la celda N9 hemos calculado el estadístico H, que es el estadístico de la prueba y finalmente al comparar con el valor crítico decidimos rechazar la hipótesis formulada, lo que significa que existe diferencia significativa en el comportamiento de las tres empresas en términos de sus ventas. Del mismo modo podríamos afirmar que se puede seleccionar a la empresa pesquera C.



Ejemplo 08

MyBody promociona un de sus métodos de bandera a fin de reducir la cantidad de calorías mediante tres tipos de ejercicios realizados durante media hora y por tres días a la semana:
Método 1: Running,
Método 2: Break Dance,
Método 3: Subir y bajar escalera.
Los datos que se muestra en las tres primeras columnas de la hoja KruskWallis02 del archivo Estad. no paramétrica se obtuvieron de un grupo de participantes en cada método en una determinada semana. Indican estos datos que hay diferencia significativa entre los métodos en cuanto a la cantidad de caloría que se logra reducir por semana? Use α = 0.05.

Solución

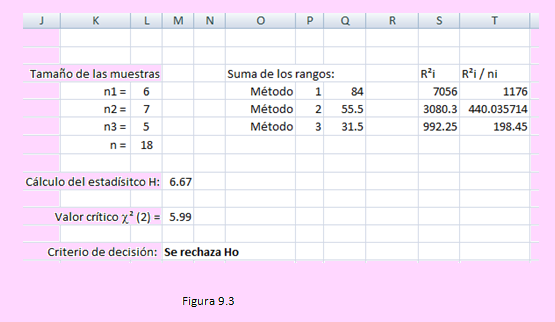
El procedimiento empleado es el mismo descrito en el ejemplo 07. La siguiente figura muestra parte de estos cálculos.

9.6 PRUEBA DE CORRELACIÓN POR RANGOS DE SPEARMAN

Esta prueba no paramétrica es utilizada para propósitos de comparación en la relación que existe entre dos variables. A diferencia de los métodos anteriores, ésta mide el grado de asociación existente entre dos variables. En el mundo real existen muchos casos en los que se desea comparar el grado de dependencia de una característica poblacional respecto de otra. Si bien el análisis de regresión se ocupa extensivamente de estos problemas, los realiza sustentado en supuestos de normalidad y un análisis de la varianza que caen en el terreno de la estadística paramétrica.

Las hipótesis a ser probadas mediante este método son:

Ho: No existe asociación entre las poblaciones
H1: Sí existe asociación entre las poblaciones

El grado de asociación entre dos variables no es otro que el coeficiente de correlación de dos variables X e Y, denotado por ρ(X,Y) o simplemente ρ. De manera que las hipótesis debieran ser:

Ho: ρ = 0
H1: ρ ≠ 0.

Para ello se usa el estadístico rS tal que



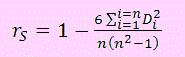
Donde D_i = R_Xi - R_Yi constituye la diferencia de los rangos entre una pareja de valores de X e Y.

Spearman demostró que para probar la hipótesis formulada se puede usar la distribución t de Student con (n-2) grados de libertad. Para ello se calcula el estadístico



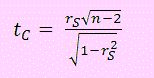
Y, se rechazará la hipótesis nula si t_C >t_1-α/2(n-2) en cuyo caso diremos que sí existe un grado de dependencia entre las dos variables.

Ejemplo 09

Un estudio de mercadeo televisivo se programó la realización de un determinado número de repeticiones de un spot referido al consumo y las bondades de un tipo de bebida energizante. Luego de este período de 30 días, se les preguntó a un grupo de televidentes que dijeran cuántas veces vieron el spot y cuántas bebidas de ese tipo habían consumido. Los datos de la misma se encuentran en la hoja CxRSpearman01 del archivo Estad. no paramétrica. A un nivel de significación del 5% ¿se puede afirmar que el spot televisivo no influyó en el consumo de la bebida?



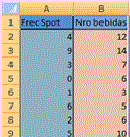
Solución

Hemos copiado los datos a las columnas E y G. En F y H se asignó el rango a cada valor y en la columna J se ha calculado el cuadrado de la diferencia de rangos. Las otras celdas de la columna J permiten obtener el estadístico de la prueba, así como el valor crítico y decidir respecto de Ho.

9.7 PRUEBA DE BONDAD DE AJUSTE

Este tipo de prueba es también considerada como no paramétrica pero se diferencia de la anteriores por cuanto se trata de determinar o identificar si un conjunto de datos puede ser “ajustada” a una distribución conocida o a una particular.

Para resolver este tipo de problemas se utiliza la distribución Chi-Cuadrado cuya fundamentación se da en el siguiente teorema.

Teorema

Si X₁, X₂, …, X_k , es un conjunto de categorías en los que se puede clasificar los resultados de las n repeticiones de un experimento, tales que p_Xi = P(X = x_i), conteniendo cada uno de ellos Oi repeticiones a las cuales las llamaremos “frecuencias observadas” tales que



Una forma de aplicar este teorema es probar el supuesto de que el conjunto de resultados tienen una particular o se puede ajustar a una distribución conocida. Según esto la hipótesis nula y alternativa en esta prueba serán:

Ho: Los datos se pueden ajustar a una distribución conocida
H1: Los datos no se pueden ajustar a una distribución conocida

O también
Ho: Los datos se pueden ajustar a una distribución particular o empírica
H1: Los datos no se pueden ajustar a una distribución particular o empírica

Criterio de decisión:

Se rechazará la hipótesis nula si
χ²_C > χ²_1-α(k-1)

Observación:

Si las frecuencias esperadas de alguna categoría fuese menor que 5 se suman con las contiguas a fin de no dispersar los resultados con lo cual se reduce el número de categorías según el número de frecuencias fusionadas, lo que afecta el valor de k.

Observación

Si el conjunto de datos deben ser ajustados a una distribución conocida, se deberá tomar en cuenta el número de parámetros a ser estimado, con lo cual, los grados de libertad a ser tomados en cuenta será: k -1 – r. Donde r representa el número de parámetros a ser estimados.

Ejemplo 10

La unidad de investigación de la Oficina de Transportes de una localidad deseaba determinar el porcentaje de tipos de vehículos que diariamente, entre las 8:00 y las 8:15 de la mañana pasan por cierta arteria de gran densidad vehicular. Esta unidad sospecha que hay 6 tipos de vehículos que con mayor frecuencia circulan en este horario por dicha arteria y que los porcentajes son de 30%, 20%, 20%, 10%, 10% y 10% de vehículos Suzuki, Nissan, Toyota, Honda, Mercedes y Kia. Para robar si estos vehículos registran este comportamiento diariamente, se registraron los vehículos que pasaron en dicho horario obteniéndose la siguiente tabla:

 

Suzuki	Nissan	Toyota	Honda	Mercedes	Kia
62	45	42	22	25	24

Estos datos confirman la sospecha de la Oficina de transportes a un nivel de significación del 5%?

Solución

Las hipótesis a ser probadas son:

Ho: La proporción de tipos de vehículos es la misma
H1: La proporción de vehículos es diferente.

En la siguiente tabla se presenta las columnas necesarias para obtener el estadístico de la prueba:

En ella el número de vehículo de cada marca representa la frecuencia observada O_i, teniendo el tamaño n = 220 y tomando los porcentajes como probabilidad de ocurrencia hemos hallado la frecuencia esperada E_i, con la cual se ha obtenido la última columna.



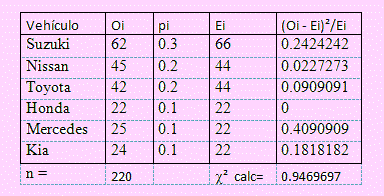
Como α = 0.05 y el número de grados de libertad es k – 1 = 6 – 1 = 5, el valor crítico será: χ²_0.95(5)= 11.0705
Como χ²_0.95(5) no es mayor que el valor crítico, no se rechaza la hipótesis nula, por lo que podemos afirmar que la sospecha de la oficina de transportes es cierta.

Ejemplo 11

Una nueva planta de fabricación de audífonos para teléfonos celulares presentaba diversos tipos de fallas. Se tomó una muestra de 200 audífonos para examinar el número de fallas que tuviera. A un nivel del 5% se puede afirmar que el número de fallas sigue una distribución de Poisson?

 

Número de fallas	0	1	2	3	4	5
Número de audífonos	40	35	38	30	32	25

Solución

Sea X la variable definida como el número de fallas encontrada en una pieza.
Si X → P (λ) entonces debemos estimar un parámetro.
Se puede demostrar que el estimador de λ es la media de la muestra,



Las hipótesis a ser formuladas son:

Ho: El número de fallas por pieza sigue una distribución de Poisson
H1: El número de fallas por pieza no sigue una distribución de Poisson

Procedimiento:

Ingresamos los datos a una hoja del Excel según se muestra en la siguiente tabla.
Calculamos la media de la muestra usando:

= SumaProducto(A2:A7,B2:B7) /Suma(A2:A7) = 2.27 Promedio de fallas La función de distribución en el caso de la Poisson es p(x)= (e^-λλ^x/x!

Usando esta función hallamos la probabilidad de que ocurra 0, 1, etc. fallas. Para ello digitamos en C2: =Exp(-2.27)*2.27^B2/fact(B2) = 0.1033

Copiamos hacia las otras celdas del rango
Calculamos la columna E. En el caso de E2: =(A2-D2)^2/D2. Copiamos hacia las otras celdas de la columna.

Los resultados se muestran en el siguiente segmento de hoja:



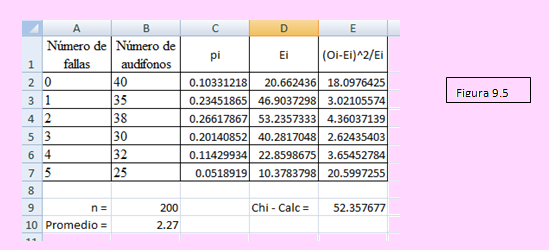
En este caso k = 6 – 1 – 1 = 4
El valor crítico es χ²_0.95(4)= 9.48773

Siendo el estadístico de la prueba mayor que el valor crítico, rechazaremos la hipótesis nula con lo cual, podemos afirmar que el número de fallas por componentes no sigue una distribución de Poisson.

Ejemplo 12

La inversión en publicidad realizada por las diversas empresas del sector industrial se muestra en la siguiente tabla en el cual se tiene el número de empresas y el monto promedio de sus inversiones.

 

Sector A
Inversión	Nro de empresas
75	10
85	15
95	40
105	25
115	10

¿A un nivel de significación del 5% es razonable pensar que el monto de las inversiones de estas empresas se ajusta a una distribución normal?

Solución

Ante todo ingresamos la tabla a una hoja del Excel, como se muestra en el siguiente segmento de hoja:



Si se trata de ajustar a una distribución normal, debemos estimar dos parámetros.
En este caso la media y la varianza.



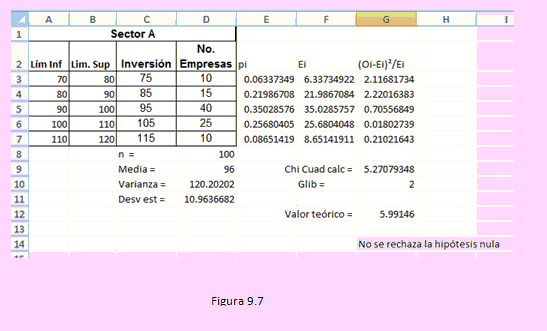
Ahora vamos a desagregar el punto medio (Inversión) en los límites inferior y superior del intervalo. La siguiente tabla muestra estos intervalos:
Ahora calcularemos las probabilidades de que un cierto monto de la inversión esté en un intervalo. Es decir,
p(X_i) = P(LimInf_i ≤ X_i ≤ LimSup_i ) = F(LimSup_i ) - F(LimInf_i)

En Excel:
=DISTR.NORM(B3,$D$9,$D$11,1)-DISTR.NORM(A3,$D$9,$D$11,1)

Esto es lo que se muestra en la columna E.

En la columna F se ha calculado Ei usando = np_i

Ahora bien, la columna D contiene los Oi, la columna F los Ei; con ellos hemos calculado G. En G9 se tiene el valor del estadístico de la prueba.

Como el número de grados de libertad es K-1 y se han estimado dos parámetros entonces el valor crítico es χ²(2) = 5.99146

Según el criterio de decisión, no se rechaza la hipótesis nula, lo que significa que los datos se pueden ajustar a una distribución normal.

Los cálculos realizados se muestran en la siguiente tabla

9.8 PRUEBA DE INDEPENDENCIA DE CRITERIOS

En muchos casos se desea probar si existe relación entre dos criterios correspondientes a una variable o entre dos categorías de valores correspondientes a una o dos poblaciones.

Por ejemplo: Una tienda comercial está interesada en saber si las ventas semanales de artefactos de cocina tienen alguna relación con el nivel socioeconómico de los consumidores. Con este motivo se tomó una muestra la que se presenta en la siguiente tabla.



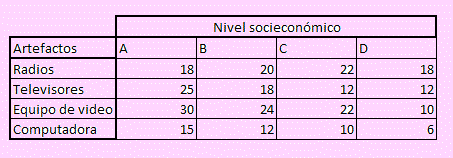
Como se puede apreciar, la variable ventas semanales de artefactos se ha dividido en dos categorías: Tipo de artefacto y nivel socioeconómico de los clientes.
Por ello las hipótesis a ser probadas serán:
Ho: La venta de artefactos es independiente del nivel socioeconómico
H1: Existe una relación entre la venta de artefactos y el nivel socioeconómico

Fundamento del método:

Sean X₁, X₂,…, X_k y Y₁, Y₂,…, Y_m dos conjuntos de valores correspondientes a dos criterios en los que se puede dividir una variable.

Sea p_ij = P(X = X_i ,Y = y_j) la probabilidad de que un elemento de la población corresponda al i-ésimo nivel de criterio X y al j-ésimo nivel del criterio Y.

Del mismo modo, p_i = P(X = x_i) y, p_j = P(Y = y_j) serán las probabilidades marginales de X e Y, respectivamente.

Si los criterios X e Y no van a estar relacionados entonces se debe tomar en cuenta que p_ij = p_i*p_j para todo i = 1, 2,…, k; j = 1, 2,…, m.

Luego las hipótesis a ser probada será:

Ho: p_ij = p_i*p_j i = 1, 2… k; j = 1, 2… m
H1: Existe por lo menos un p_ij ≠ p_i*p_j para algún i ≠ j.

Estadístico de la prueba:

Sea O_ij el número de elementos que corresponden al i-ésimo criterio X y j – ésimo criterio Y; es decir, O_ij será la frecuencia observada.

La siguiente tabla muestra la distribución de la muestra de acuerdo a las dos categorías, lo que se conoce también como una tabla de contingencia.



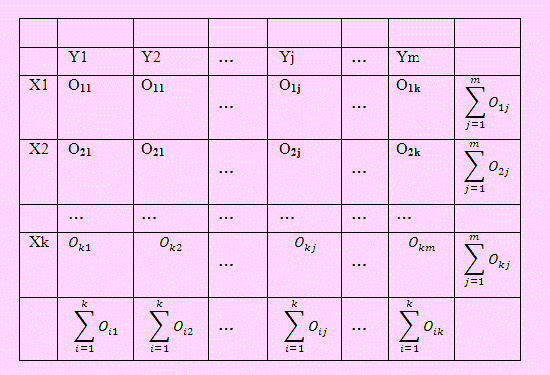
De acuerdo a esto las estimaciones de las probabilidades marginales serán:



El número de grados de libertad será (k-1)*(m-1) con el cual se podrá obtener el valor crítico con 100α% de nivel de significación.

Criterio de decisión:
Si χ²_C > χ²_1-α (k-1)(m-1) se rechazará la hipótesis nula

Ejemplo 13

Tomemos el problema descrito al inicio de esta sección. ¿A un nivel de significación del 5% se puede afirmar que las ventas semanales de artefactos de dicha tienda son independientes con el nivel socioeconómico de los consumidores?

Solución

De acuerdo a la pregunta formularemos las siguientes hipótesis:
Ho: La venta semanal por tipo de artefactos es independiente del nivel socioeconómico en dicha tienda.
H1: Las ventas semanales por tipo de artefactos y el nivel socioeconómico no son independientes.
Cálculo del estadístico de la prueba:

Procedimiento:

Ingresamos los datos en una hoja del Excel, como se muestra en la figura

 

	Frecuencias observadas
Artefactos	A	B	C	D	Total
Radios	18	15	25	18	76
Televisores	25	18	12	25	80
Equipo de video	30	24	22	10	86
Computadora	15	12	10	16	53
Total	88	69	69	69	295

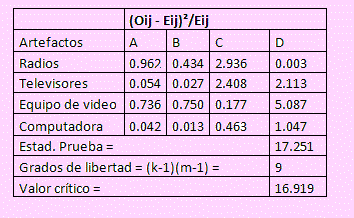
La columna F contiene la suma de las frecuencias por artefacto. La fila 7 contiene la suma de las frecuencias por nivel socioeconómico. La celda F7 contiene el tamaño de la muestra



A continuación obtenemos la matriz de los p_ij = O_ij/274 con lo cual, sumando por fila obtenemos los p_i. y p_.j que son las proporciones marginales. Esto se aprecia en la siguiente figura



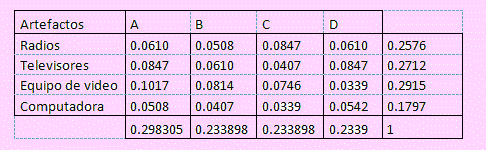
A partir de esta matriz obtenemos otra que constituye la matriz de las frecuencias esperadas E_ij = np_i. p_.j lo que se muestra en la siguiente figura



Valor crítico = ²(9) = 16.919

Criterio de decisión:
Como el valor calculado es mayor que el valor crítico, rechazamos la hipótesis nula; esto significa que las ventas semanales de los artefactos en dicha tienda dependen del nivel socioeconómico de los consumidores.

Nota:

El archivo Prueba de independencia contiene la solución de este problema en su primera hoja.

La siguiente tabla muestra los resultados finales



Ejemplo 14

Tres expertos fueron convocados para evaluar un lote de los primeros 500 productos con los que Perú iniciaba su comercio con Malasia. Ellos deberían clasificar a los productos de acuerdo a estándares internacionales en tres calidades C1, C2 y C3. La siguiente tabla muestra los resultados después de ser evaluados por los expertos. ¿A un nivel de significación del 5% se puede afirmar que la calificación de estos expertos es independiente de las certificaciones de calidad?

 

	Frecuencias observadas
	E1	E2	E3
C1	70	60	30
C2	50	80	55
C3	35	70	50

Solución

Las hipótesis que corresponden a este problema son
Ho: La calificación de los expertos es independiente a la calidad de los productos.
H1: La calificación de los expertos depende de la calidad de los productos.
La solución se encuentra en la hoja 2 del archivo mencionado líneas arriba.

Procedimiento utilizado

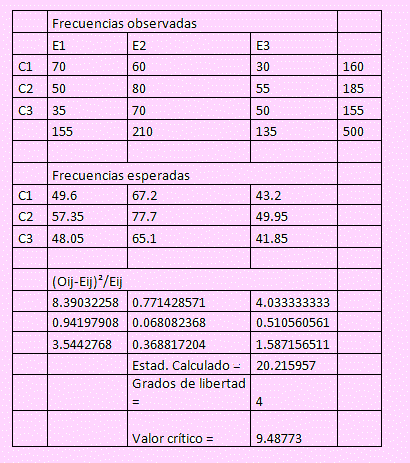
Aquí hemos variado el procedimiento:
Primero hemos obtenido los totales por fila y por columna

Utilizando la fórmula: Total Fila_i/500*Total Col_j/500*500 hemos obtenido la matriz E_ij.

La tercera matriz se ha obtenido usando la fórmula:
(O_ij - E_ij )²/E_ij

Estadístico de la prueba:

En la celda D17 se ha obtenido el valor del estadístico de la prueba =20.215957
El número de grados de libertad = (k-1) (m-1) = 4.
El valor crítico Chi cuadrado con 4 grados de libertad =9.48773
Usando el criterio de decisión podemos afirmar que la calificación de los expertos no es independiente a la clasificación de dicho producto.

La siguiente tabla muestra las tres matrices usadas en la solución de este problema.

9.9 PRUEBA DE HOMOGENEIDAD DE PROPORCIONES

Una tercera aplicación de la distribución Chi-cuadrado, dentro de la estadística no paramétrica es aquella que se refiere a pruebas de comparación del comportamiento de dos o más muestras; esto es, afirmar que todas las muestras provienen de la misma población o de poblaciones iguales y como tal, son homogéneos en su comportamiento.

De manera que si se toman k muestras aleatorias extraídas de igual número de poblaciones y son clasificados en m grupos o criterios pre definidos, entonces O_ij representará el número de observaciones proveniente de la i-ésima población, perteneciente al j-ésimo criterio.

Esto sugiere el uso de la siguiente tabla en la cual se tendrán las observaciones.



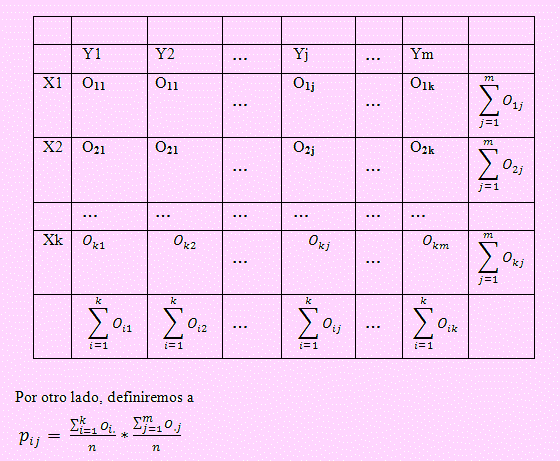
como la proporción de que una observación cualquiera de la i-ésima población, corresponda al j-ésimo criterio.

Como se podrá apreciar, el procedimiento a seguir será similar a la prueba de independencia de criterios ya los datos tienen la misma estructura y se toma en cuenta la probabilidad de pertenencia de una observación a un criterio.

En tal sentido, las hipótesis a ser formuladas serán:

Ho: Todas las muestras presentan las mismas características o todas las muestras proceden de la misma población
H1: Las muestras difieren en su comportamiento o no es cierto que todas las muestras procedan de la misma población.

Otra manera de formulas las hipótesis es utilizando la proporción de observaciones por criterio:

Ho: p_1j = p_2j = ⋯ = p_kj
H1: p_1j ≠ p_hj para algún i ≠ h Estadístico de la prueba:



Grados de libertad:
Como en el modelo anterior el número de grados de libertad será: (k-1) (m-1).

Criterio de decisión:
Si  χ²_C  >  χ²_1-α(k-1)(m-1) entonces rechazaremos la hipótesis nula.

Ejemplo 15

Debido a la crítica situación del equipo Alianza Lima, una firma comercial que desea participar en la solución, decidió llevar a cabo una encuesta a los socios de tres de los distritos más identificados con el club, para saber su opinión respecto a la actual directiva. Los resultados de la muestra se presentan en la siguiente tabla:

 

	Distritos
Opinión	A	B	C
A favor	30	24	30
En contra	15	20	18
Indiferente	15	16	12

A un nivel de significación del 5% ¿se puede afirmar que la opinión de los socios es la misma en los tres distritos?

Solución

Ingresamos los datos a una hoja del Excel.

Como en el segundo ejemplo modelo anterior, obtenemos las sumas por fila y columna.

Obtenemos las frecuencias esperadas E_ij



Con lo cual obtenemos el estadístico de la prueba: χ²_C = 2.178775

El valor crítico es χ²_0.95(4) = 9.48773

Como el estadístico de la prueba no es mayor al valor crítico, no se rechaza la hipótesis nula; en consecuencia, podemos afirmar que la opinión de los socios es la misma en cualquiera de los tres distritos.

Nota

Todo el problema se encuentra en la hoja Homg1 del archivo Test indep.

Ejemplo 16

El administrador de peajes de la municipalidad de Lima desea saber si hay diferencia en la proporción de vehículos manejados por un hombre o una mujer, que pasan por una caseta de control en ciertas horas de un fin se semana largo. Para realizar el estudio se observaron a 1000 vehículos que pasaron por dicha caseta, obteniéndose los siguientes resultados:



A un nivel de significación del 5% ¿se puede afirmar que no existe diferencia significativa en la proporción de vehículos que pasan por la caseta en los intervalos considerados?

Solución

Ingresamos la tabla a una hoja del Excel.

Como ya se tienen los totales, pasamos a calcular la matriz de las frecuencias esperadas, lo que se muestra en la siguiente tabla:



Obtención del estadístico de la prueba: χ²_C = 19.35763889

El número de grados de libertad = 2

El valor crítico = χ²_0.95(2) = 5.99146

Luego, como la hipótesis nula se rechaza, podemos afirmar que sí existe diferencia significativa en la proporción de vehículos que pasan por la caseta en los intervalos considerados.

Nota:

La solución al problema se encuentra en la hoja Homg2 del archivo TestIndep.xlsx.

9.10 PROBLEMAS PROPUESTOS

1. Una agencia de viajes está interesada en saber si el porcentaje de familias que asistirán a las 5 playas de su interés, cambiarán para este verano. Los porcentajes de familias que asistieron los fines de semana del verano pasado se muestra en la siguiente tabla.

 

Playas	1	2	3	4	5
Porcentaje	10	35	10	20	25

Para averiguar si este comportamiento había cambiado, se tomó una muestra de 2000 asistentes a las playas en la última semana, obteniéndose los siguientes resultados:

 

Playas	P1	P2	P3	P4	P5
Nro de familias	200	750	320	350	280

Usando α = 0.05, pruebe usted si los porcentajes de asistentes a las diferentes agencias cambió de manera significativa.

2. Una tienda de ropa femenina desea promocionar tres de sus prendas de mayor demanda, para el próximo verano: polos Z1, toallas y pareo. En la publicidad ofrece un descuento por temporada del 25% por cada una de estas prendas. Para saber si puede colocar más prendas en el mercado, realiza una encuesta sobre la preferencia de estas prendas. La muestra se llevó a cabo con 300 de sus clientes potenciales del último fin de semana. La información obtenida se muestra en la siguiente tabla:

 

Prendas	Polo Z1	Toalla	Pareo
Preferencia	110	105	85

A un nivel de significación de 5%, ¿hay alguna preferencia por alguno de los regalos o todos son igualmente deseados?

3. PCB es una caja municipal de provincia con gran demanda en el mercado de prestamistas que no acuden a una entidad financiera o bancaria. En su idea de penetrar al gran mercado limeño, desea estudiar el número de solicitudes de crédito recibidas por día en el último semestre, 180 días por las diversas entidades financieras y bancarias de Lima, obteniéndose la siguiente información:

 

Nro solicitudes de crédito	0	1	2	3	4	5 ó más
Frecuencia(nro de dís)	50	77	81	48	33	11

A un nivel del 5%, ¿sería razonable concluir que la distribución del número de solicitudes diarias de préstamo es del tipo Poisson, con una media igual a 2?

4. El número de visitantes a un determinado museo durante una semana cualquiera parecen seguir una distribución normal, pues eso es lo que se puede deducir de las observaciones obtenidas durante 5 días de lunes a viernes, lo cual está contenido en la siguiente tabla en la cual se indica el monto recaudado por día, siendo X el punto medio de cada intervalo y fi el número de visitantes corresponde el valor central de cada intervalo.

 

	Lunes	Martes	Miercoles	Jueves	Viernes
Xi	300	500	700	900	1100
fi	30	50	90	45	35

A un nivel del 5% ¿se puede afirmar que el número de visitantes al museo sigue una distribución normal?

5. A un curso de Juego de Bolsa asistieron 50 administradores, 40 ingenieros y 10 contadores. Con la intención de formar grupos afines, se les consultó si creen que las acciones mineras bajarían, subirían o se mantendría igual, en la próxima semana. El 20% de los administradores opinaron que subiría, mientras que el 40% de ellos piensa que bajará. El 50% de los ingenieros se inclinaron por que permanecerían igual y sólo el 5% creen que bajaría. La mitad de los contadores se inclina por la subida y la otra mitad por la bajada.

Tomando en cuenta esta información y con un nivel de significación del 5%, ¿existe alguna relación entre el comportamiento del mercado bursátil y la profesión del encuestado?

Siguiente sesión.