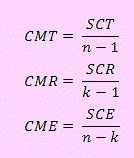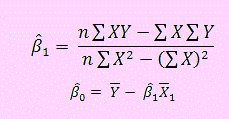CAPÍTULO 10

REGRESIÓN LINEAL

10.1 Introducción
10.2 Estimación de parámetros y prueba de hipótesis en el modelo lineal
10.3 Problemas propuestos

10.1 INTRODUCCIÓN

En los capítulos anteriores en varias ocasiones hemos hablado de más de una variable. Por ejemplo cuando hablamos de variables aleatorias bidimensionales, dijimos que dos variables aleatorias estarán relacionadas si su covarianza es diferente de 0.

Si la covarianza es positiva entonces existe una relación directa positiva; es decir, si una variable aumenta, entonces también aumenta la otra; por el contrario si la covarianza es negativa entonces existe relación inversa; lo que significa que cuando una aumenta, la otra disminuye. Por otro lado, si la covarianza es cero, dijimos que las dos variables no están relacionadas; es decir, son variables aleatorias independientes.

En la práctica existen muchos casos en los cuales dos o más variables aleatorias están relacionadas.

¿Qué significa que dos o más variables están relacionadas?

Significa que entre ellas existe una relación funcional de la forma y = f(x) en el caso de dos variables y cuando se tiene más de dos variables entonces el modelo será

y = f(x₁, x₂ , … , x_n).

En esta caso tendremos el modelo en el cual la variable Y está en relación de X₁, X₂, … , X_n1; es decir, Y depende de los Xi.

Según esto, Y recibe el nombre de variable dependiente y X₁, X₂, … ,X_n constituyen las variables independientes.

Veamos el caso de la venta del pollo: Cuando la demanda del pollo aumenta, el precio también aumenta; sin embargo, cuando la oferta aumenta, el precio del pollo disminuye. Esto lo saben todas las amas de casa que diariamente hacen el mercado.

De manera que, si se desea analizar si dos o más variables están relacionadas, debemos obtener un modelo matemático que nos permita construir dicha relación.

Y ¿por qué tenemos que estudiar la relación entre dos variables? Si se tiene el modelo podemos realizar proyecciones futuras las que nos permitirá realizar una adecuada toma de decisiones.

Sin embargo, antes de construir el modelo matemático, debemos realizar un análisis de dispersión de las variables dos a dos; entre la variable dependiente y una de las variables independientes. La forma cómo se muestran los puntos en este gráfico nos indicará qué modelo construir.

En el presente capítulo estudiaremos el modelo lineal cuyo modelo matemático se representará como

 Y = β₀ + β₁ X₁ + β₂ X₂ + … + β_n X_n + ε

denominado modelo de regresión lineal múltiple.

Cuando se trata de un modelo de dos variables entonces tendremos Y = β₀ + β₁ X₁ + ε denominado modelo de regresión lineal simple. En ambos modelos ε es una variable llamada variable estocástica que representará los errores que afectan a Y, pero que no son explicados por el modelo, el cual se sustenta en los siguientes supuestos:

E(ε ) = 0
V(ε) = σ²

Y que las variables ε₁ no están correlacionadas.

10.2 ESTIMACIÓN DE PARÁMETROS Y PRUEBA DE HIPÓTESIS EN EL MODELO LINEAL

Antes de hablar del modelo lineal, veamos el siguiente ejemplo:

En la página 297 del libro Problemas Econometría, A. Aznar y A. García proponen como problema 4.22 el siguiente caso: Evaluar los efectos de la “revolución verde” tomando una muestra entre los años 1957 a 1976 sobre de la producción agrícola española, Y_i, conjuntamente con el volumen de fitosanitarios, X₁, de la maquinaria agrícola, X₂ y del financiamiento público y privado, X₃. Los datos se muestran en la siguiente tabla:



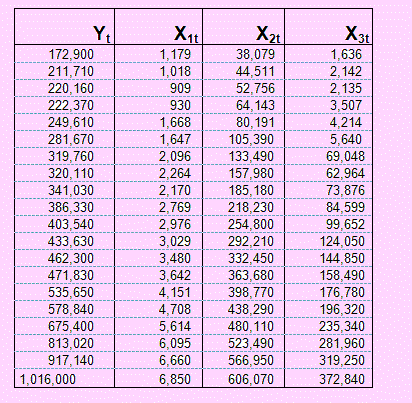
El problema consiste en comprobar si la producción agrícola depende del volumen de fitosanitarios, de la maquinaria y parque automotor y del financiamiento público y privado.

Lógicamente la sola definición de las variables sugiere un modelo de la forma

Y_i = β₀ + β_i X_i1 + β₂ X_i2 + β₃ X_i3 + ε_i

Pero antes de formularlo, deberíamos estar seguros que será este el modelo. Para ello hemos realizado un análisis de gráficos utilizando el diagrama de dispersión entre la producción agrícola y cada una de las variables independientes. Todo este análisis exploratorio de datos (EDA) lo hemos realizado en el archivo RegreLineal.xlsx, uno de cuyos gráficos mostramos aquí.



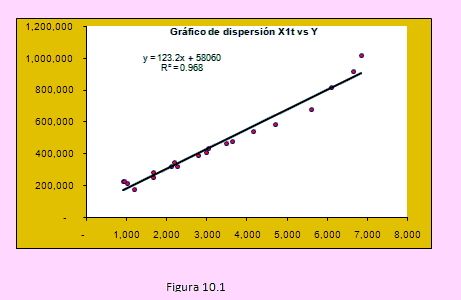
Este gráfico de dispersión, realizado en Excel nos dice que la producción agrícola está en relación con el volumen de fitosanitarios. Observen que Excel nos permite obtener la relación lineal Y = 58060 + 123.2X₁

De manera que el modelo lineal general será el siguiente:

Y_i = β₀ + β₁ X_i1 + β₂ X_i2 + β₃ X_i3 + …+ β_k X_ik + ε_i     (1)

Donde

Y representa la variable dependiente o variable explicada

X₁, X₂,…, X_k representan las variables independientes o variables explicativas

k representa el número de variables independientes

β₀ es el intercepto o valor inicial de Y cuando todos los X_i son iguales a 0.

 β₁,β₂ ,…,β_k son los coeficientes de regresión.

Y ε_i es una variable estocástica que debe cumplir los siguientes supuestos:


El objetivo es obtener los valores críticos que hacen que la sumatoria del lado izquierdo sea mínimo. Estos valores críticos son los estimadores de cada uno de los parámetros β_i del modelo.

El procedimiento para obtener estos estimadores es el método de los Mínimos Cuadrados Ordinarios (MCO), estudiado en el capítulo de estimación puntual.

De manera que

Si β₀, β_i, β ₂,….,β_k son los estimadores de los coeficientes de regresión que han sido obtenidos por dicho método, entonces el modelo estimado será

Y^s_i = β^s₀ + β^s₁ X_i1 + β^s₂ X_i2 + …+ β^s_k X_ik     (3) Donde Y^s_i representa el estimador de Y, conocido también como Y pronosticado o Y predicho.

Propiedades de los estimadores

El estadístico β^s es un estimador insesgado de β; es decir, E(β^s) = β
El estadístico β^s₀ es un estimador insesgado de β₀; es decir, E(β^s₀) = β₀

Ahora bien, restando (3) de (1) obtendremos Y - Y^s lo cual puede interpretarse como



Los grados de libertad correspondientes son:

Para SCT es (n-1) donde n es el tamaño de la muestra

Para SCR = (k-1) donde k es el número de variables en el modelo.

Para SCE = (n-1) – (k-1) = (n-k)

Luego, dividiendo cada suma de cuadrados entre sus respectivos grados de libertad tendremos los cuadrados medios que constituyen las varianzas respectivas.



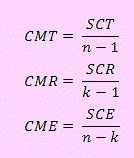
Finalmente, con toda esta información podemos construir la tabla del análisis de varianza para un modelo de regresión lineal general:



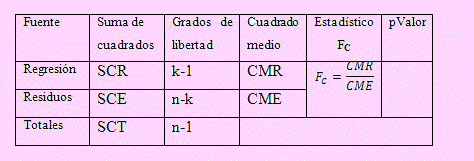
Coeficiente de determinación

r² = SCR/SCT

representa la proporción de veces que la variación de la variable dependiente Y, es explicada por el modelo; por lo general se interpreta en forma porcentual. A diferencia del coeficiente de correlación entre dos variables, 0 ≤ r² ≤ 1.

Mientras ρ(X, Y) cuantifica el grado de relación entre dos variables, r² indica el porcentaje de veces que el modelo se adecúa para estimar, pronosticar o predecir los valores de Y.

Observación

En algunos casos o en ciertas situaciones, es más conveniente usar el coeficiente de determinación ajustado r²_a = 1 – (1-r²) (n-1)/(n-1-k)

Coeficiente de correlación entre dos variables de la muestra

Definiremos a r(X, Y) es el coeficiente de correlación de la muestra entre las variables X e Y (tomado a X como una sola variable) como
r(X,Y)=(signo de β)√(r² ) y su interpretación es la misma dada anteriormente.

Análisis del modelo lineal simple

Estimación de los parámetros:

En el caso de un modelo lineal simple tendremos
Y_i = β₀ + β₁ X_i1 + ε_i
Y^s_i = β ₀ + β^s₁ X_i1

En el capítulo de estimación de parámetros estudiamos el método de los mínimos cuadrados ordinarios para estimar los coeficientes de un modelo lineal.

Dicho método nos permite encontrar



Estimación de la varianza de los coeficientes de regresión



Estimación por intervalos

A continuación obtendremos intervalos de confianza del 100(1-α) % para cada uno de los coeficientes de regresión y para Y estimada.

Intervalo de confianza para β₁
Si tomamos en cuenta el supuesto de normalidad para ε entonces, por la propiedad reproductiva de la normal Y también será normal; esto es, supondremos que la muestra usada proviene de una población normal.

Según esto y si consideramos que el estadístico β ̂_1 es una variable muestral, entonces, la variable
T =(β^s₁ -β₁)/σ_β1 ) tendrá una distribución t con (n-2) grados de libertad.
Por lo que el intervalo de confianza del 100(1-α) % para β₁ será:



Puesto que Y se puede predecir como Yo, dada la ocurrencia de un evento en X; es decir, que ocurra X = Xo entonces podemos saber el valor esperado de Yo, dado X = X_o; en otras palabras, podemos estimar por intervalos a E (Y_o/X = X_o) = μ_Yo )



Prueba de hipótesis

Una primera hipótesis de trabajo surge de inmediato cuando se pretende cuestionar si realmente la variable explicada Y se ajusta al modelo estimado o, si la relación obtenida es significativa.

Por otro lado, puesto que una variable puede depender de otra según el valor del coeficiente de regresión correspondiente, es lógico que nuestros modelos de hipótesis tengan que formularse también respecto los coeficientes β₀ y β₁.

Prueba de hipótesis para la regresión:

Ho: ρ(X, Y) = 0: La variable Y no puede ser ajustada por el modelo de regresión
H1: ρ(X, Y) ≠ 0 Las dos variables están correlacionadas.

Estadístico de la prueba:

De acuerdo a la tabla del ANOVA, el estadístico de la prueba es F_C = CMR/CME


Valor crítico de la prueba:

Como en el caso general el número de grados de libertad de SSR es (k-1) en el modelo lineal simple k = 2; por tanto, los grados de libertad del numerador será 1 y del denominador, (n-k) = (n-2).

Luego debemos hallar el valor crítico para F_1-α (1,n-2)

Criterio de decisión

Si F_C > F_1-α(1,n-2) rechazaremos la hipótesis nula, con lo cual estaremos afirmando que el modelo no explica significativamente la variabilidad de la variable dependiente Y.

Prueba de hipótesis para β₁:

H0: β1 = 0
H1: β1≠ 0

Estadístico de la prueba:
t_C = β^s₁/σ_β^s0 )

Valor crítico:
t_1-α/2(n-2)

Criterio de decisión:
Si t_C > t_1-α/2(n-2) se rechazará la hipótesis nula; es decir, las variables aleatorias son independientes.

Prueba de hipótesis para β0:
Ho: β₀ = 0
H1: β₀ ≠ 0

Estadístico de la prueba:
t_C = β^s₀/σ_β0 )

Valor crítico:
t_1-α/2(n-2)

Criterio de decisión:
Si t_C > t_1-α/2(n-2) se rechazará la hipótesis nula; es decir, las variables aleatorias tienen un intercepto común en el origen de coordenadas.

Análisis del modelo lineal general

En este caso la estimación de los parámetros de la regresión se deduce usando matrices:
Desde el punto de vista matricial, el modelo es Y = βX + ε , donde



El análisis de un modelo lineal múltiple se basa en todo lo dicho para el modelo lineal simple Y= β₀ + β₁ X₁ + ε dejaremos de lado las deducciones tanto a nivel de estimación puntual, por intervalos como para las pruebas de hipótesis.

Nos dedicaremos a resolver modelos de más de dos variables mediante el programa Excel.

Prueba de hipótesis en el modelo lineal general

H0: β₁ = β₂ = … = β_k = 0 : La variable Y no es ajustada por el modelo de regresión
H1: β_i ≠ 0 para algún i = 1, 2,…, k: Una de las variables independientes contribuyen significativamente al modelo.

Estadístico de la prueba:

Como la tabla del ANOVA, nos proporciona este estadístico Entonces el estadístico de la prueba es
F_C = CMR/CME

Valor crítico de la prueba:

En el caso general el número de grados de libertad de SSR es (k-1) por lo que los grados de libertad del numerador será (k-1) y del denominador, (n – k -1) Luego debemos hallar el valor crítico para F_1-α (1,n-k-1)

Criterio de decisión
Si F_C > F_1-α (1,n-k-1) rechazaremos la hipótesis nula, con lo cual estaremos afirmando que el modelo no explica significativamente la variabilidad de la variable dependiente Y.

Prueba de hipótesis para βj:
H0: β_j = 0 La variable Y no depende de la j-ésima variable independiente
H0: β_j ≠ 0 La variable Y la j-ésima variable presentan alguna relación.

Estadístico de la prueba:
t_C = β^s_j/σ_{β^s j} )

Valor crítico:
En este caso los grados de libertad para t serán (n-k-1)
t_1-α/2 (n-k-1)

Criterio de decisión:
Si t_C > t_1-α/2 (n-k-1) se rechazará la hipótesis nula; es decir, las variables aleatorias tienen un intercepto común en el origen de coordenadas.

Nota:

En los ejemplos que a continuación desarrollaremos, usaremos extensivamente todo los que el Excel nos proporciona como herramienta para resolver el problema.

Ejemplo 01

La gerencia de personal de una empresa desea elevar la eficiencia de sus empleados controlando el tiempo que tardan en el ensamble de celulares. Para ello somete a 10 de sus empleados a una prueba que consiste en registrar el tiempo de ensamble de un celular y someterlo a un riguroso control de calidad. El tiempo registrado por cada uno de ellos y la eficiencia alcanzada, se muestra en la siguiente tabla.

 

Tiempo (minutos)	27	45	41	19	35	39	19	49	15	31
Eficiencia(%)	47	84	80	46	62	72	52	87	37	68

a) Obtenga un diagrama de dispersión y diga a qué modelo se puede ajustar los datos. Identifique la variable independiente y la variable dependiente.
b) Calcule e interprete el valor de cada uno de los coeficientes de la recta de regresión
c) ¿Qué indica el valor del coeficiente de determinación?

Solución

a) Procedimiento:
- Ingresemos los datos al Excel a partir de A1 colocando como nombre de columna: Tiempo y Eficiencia. La variable Tiempo será la variable independiente y Eficiencia será la variable dependiente.
- Construiremos el diagrama de dispersión: Seleccionamos el rango A1:B11; usamos la secuencia [Insertar] - [desplegamos la lista de dispersión ] - seleccionamos “Dispersión solo con marcadores”
- Observando el gráfico podemos afirmar que existe una relación entre el tiempo que se tarda en ensamblar el celular y la eficiencia obtenida. Esta es una relación directa pues a mayor tiempo de ensamble mayor porcentaje de eficiencia.



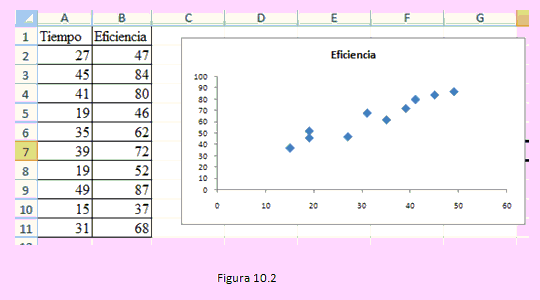
- Vamos a añadir al gráfico Línea de tendencia. Estando seleccionado el gráfico - [Línea de tendencia ] - [Más opciones línea de tendencia]. En la ventana siguiente debe quedar activada Lineal, Presentar ecuación en el gráfico y Presentar el valor R cuadrado en el gráfico. Luego clic en [Cerrar].
- Podemos apreciar que el modelo es adecuado para explicar el comportamiento de la eficiencia en términos del tiempo de ensamble en el 91.5% de las veces. La ecuación de regresión estimada es:

Eficiencia = 18.06 + 1.42 Tiempo.

 Gracias al modelo podemos decir, si el tiempo de ensamble es de 20 minutos, el porcentaje de eficiencia alcanzado será de 18.06 + 1.42 (20) = 46.46%

- Estimaremos los coeficientes de regresión usando el Excel.

En este ejemplo no usaremos la función Estimacion.Lineal ni la herramienta Regresión.



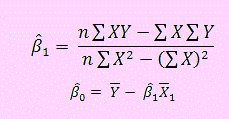
- Como en D15 ingresamos la fórmula que calcula el coeficiente β₁, entonces

=(D14*SUMAPRODUCTO(A2:A11,B2:B11)-SUMA(A2:A11)*SUMA(B2:B11))/(D14*SUMA.CUADRADOS(A2:A11)-SUMA(A2:A11)^2)

En D17 ingresamos la fórmula que calcula el intercepto β₀:
=PROMEDIO(B2:B11)-D15*PROMEDIO(A2:A11)

Interpretación:
En cuanto a β₀ : Si el tiempo de ensamble es 0, la eficiencia es de 18.06%. Aunque en este problema la eficiencia debiera iniciarse en 0, podríamos interpretarla como eficiencia inicial. Un ajuste más adecuado al problema podría ser obtener la ecuación cuando este coeficiente es 0.



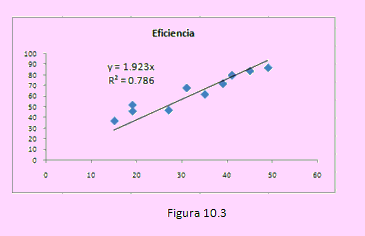
La gráfica que acompañamos en el libro que estamos usando, indica que en tal caso la ecuación con el origen en 0 será Eficiencia = 1.923 Tiempo sólo que, como se puede apreciar, el coeficiente de determinación ha disminuido. Antes era de 91.5%.

Ahora es sólo de 78.6% lo que indicaría que se logra mejor ajuste cuando no se realiza una transformación de eje. Sin embargo, si el tiempo de ensamble es de 20 minutos, la eficiencia obtenida es de 38.46%. Es más comprensible que estar asumiendo una eficiencia inicial de 18.06%.

En todo caso la duda será resuelto por los que tomen las decisiones frente a un caso.

b) Para responder a esta pregunta usaremos el coeficiente de determinación obtenido en el gráfico al añadirle la línea de tendencia.

En el siguiente ejemplo obtendremos este coeficiente por otros medios. Según esto, r²% = 91.5% permite afirmar que los datos pueden ser representado por el modelo en el 91.5% o que el modelo explica el comportamiento de los datos en el 91.5% de las veces.

La solución y gráfica en Excel se encuentra en la hoja llamada Ejemplo del archivo Regresión lineal.

Cómo estimar los parámetros en Excel

El programa Excel dispone de una función: Estimacion.Lineal (…) y de una herramienta Regresión para resolver problemas de aplicación de un modelo lineal general o regresión múltiple.

Uso de la función Estimacion.Lineal(…)

En Excel usaremos la función
=Estimacion.Lineal(VarY,VarX,Intercepto,Detalle)

Donde
VarY constituye el rango de la variable dependiente
VarX es el rango o matriz que incluye a todas las variables independientes
Intercepto, que puede ser Verdadero o Falso. Verdadero permite obtener el estimador del intercepto βo. Se puede usar 1 ó 0 en lugar de Verdadero o Falso.
Detalle, que también puede ser Verdadero o Falso, permite incluir el detalle (Cuadro del ANOVA) o sólo el coeficiente de determinación.

Esta función permite emitir la siguiente tabla:



Descripción de esta tabla:

La primera fila contiene los valores de los coeficientes de regresión en orden inverso; es decir, b es el intercepto, m₁ es el coeficiente de X₁,…, m_n es el coeficiente de X_n. La segunda fila contiene los errores estándar de las variables y del intercepto
La tercera fila contiene el coeficiente de determinación r²; y el error estándar de Y
La cuarta fila contiene el estadístico de la prueba F_C y los grados de libertad del modelo.
La quinta fila contiene la suma de los cuadrados de la regresión y de los residuales.

Observación importante:
Para usar esta función primero se debe seleccionar un rango formado por 5 filas por lo descrito anteriormente y tantas columnas como variables tenga el modelo (incluyendo la variable dependiente).
Digitar la función con todos sus argumentos (estando seleccionado el rango)
Teniendo presionada las teclas [Ctrl]+[SHIFT] y presionar una sola vez la tecla [Enter]

Ejemplo 02

Tomemos como ejemplo el caso planteado al inicio de este capítulo sobre la producción agrícola española entre los años 1957 a 1976.
Haga un análisis completo de este problema tomando en cuenta los siguientes criterios:
Construya los diagramas de dispersión necesarios a fin de tener una idea clara sobre el modelo que explique la variabilidad de la producción agrícola
Obtenga una matriz de correlación a fin de realizar un análisis previo de relación entre pares de variables.
Obtenga una matriz de correlación a fin de observar el grado de correlación existente entre las variables de este problema.

Finalmente, a un nivel de significación del 5% ¿se puede afirmar que la producción agrícola depende de las otras tres variables?

Solución

Sea Yt la variable definida como la producción agrícola total
X_1t la variable definida como el volumen de fitosanitarios utilizado
X_2t la variable que representa el parque de maquinaria agrícola
X_3t la variable que representa el financiamiento público y privado

Ingresamos primero los datos a una hoja de Excel. Esto lo encontramos en el archivo Regresión lineal.

Construimos gráficas de dispersión de las variables. En ellas podemos apreciar que la producción agrícola depende de cada una de las otras variables; por lo tanto, es muy probable que un modelo lineal explique la variación de la producción agrícola.

Para obtener la matriz de varianzas y covarianzas:
Use la secuencia: [Datos] - [Análisis = de datos ] - [Covarianza].

Complete la ventana como se muestra en la siguiente imagen:



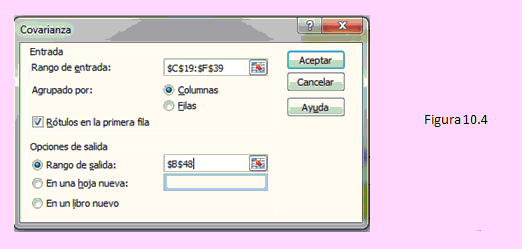
Luego de hacer clic en [Aceptar] obtendremos los resultados que se muestran



En la diagonal principal se encuentra la varianza de cada variable. Puesto que Excel calcula la varianza poblacional (Varp(…)), hemos reemplazado por la varianza de la muestra; es decir, Var (…).

La triangular inferior muestra la covarianza de pares de variables: Como se pudo apreciar en los gráficos de dispersión, cuando el volumen de fitosanitarios (X₁) aumenta, también aumenta la producción agrícola, esto se fundamenta en la covarianza de estas dos variables que es un número positivo (no interesa su valor, probablemente cuanto mayor sea la correlación entre ellas sea mayor).

Obtendremos ahora la matriz de correlación:
Usemos la secuencia: <[Datos] – [Análisis de datos] – [Correlación]. Completamos la ventana como se muestra en la siguiente imagen:



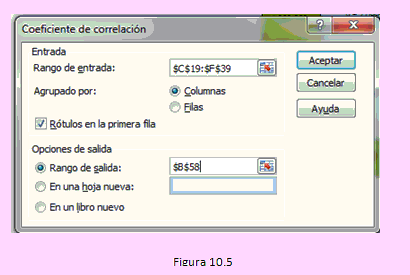
Luego de hacer clic en [Aceptar] obtendremos los siguientes resultados:



Podemos apreciar la altísima correlación entre las variables. Por ejemplo la producción agrícola y el financiamiento público y privado están correlacionados en el 99%; es decir, que la variación de la producción agrícola depende del financiamiento público en el 99% de los casos.

Pasamos a obtener la tabla del ANOVA, la que nos mostrará también la estimación de los coeficientes de regresión.

Para ello primero debemos seleccionar el rango de salida. Hemos dicho que se deben seleccionar 5 filas y tantas columnas como número de variables hay en el modelo.

Según esto,
Seleccionaremos el rango C89:F93
Ingresamos la fórmula:
=Estimacion.Lineal(C20:C39,D20:F39,1,1)



Teniendo presionada [Ctrl]+[SHIFT], presionamos una vez [Enter] Con lo cual obtendremos:



En la fila superior hemos añadido la secuencia de los coeficientes de regresión a fin de facilitar su reconocimiento.

En esta matriz de resultados tenemos:
El coeficiente de determinación: r² = 0.9875
El estadístico de la prueba: F_C = 421.6856
La desviación estándar de los errores totales: σ = 29363.70194

Encontramos también:

La suma de cuadrados de la regresión: SCR = 1.09077E+12
La suma de cuadrados de los residuos: SCE = 13795631861
Podemos hallara la suma de cuadrados totales: SCT = SCR + SCE
Número de grados de libertad para cada fuente

Los estimadores de los coeficientes de regresión:
β^s₀ = 166174.177; β^s₁ = 69.79667214, β ^s₂ = -0.706994337; β^s₃ = 2.077349096

Por tanto el modelo lineal ajustado para este problema será:

Y = 166174.177 + 69.79667214 X1 - 0.706994337X2 + 2.077349096X3

Las desviaciones típicas estimadas para cada uno de estos coeficientes son:
σ_(β ^s₀ )= 29684.20428
σ_(β ^s₁ )= 29.60358049
σ_(β^s₂ )= 0.251824119
σ_(β ^s₃)= 0.432673638

Formulación de las hipótesis:

Ho: El modelo no explica la variabilidad de la producción agrícola
H1: El modelo sí explica la variabilidad de la producción agrícola

Estadístico de la prueba:
F_C = 421.6856
El valor crítico: Cualquier valor crítico con un nivel de 5% es menor que Fc, por tanto rechazamos la hipótesis nula; esto significa que el modelo explica el comportamiento de los datos.

Del mismo modo, el coeficiente de determinación también indica el alto grado de explicación de los datos mediante el modelo estimado.

Uso de la herramienta Regresión

Vamos a resolver el mismo problema usando la herramienta [Regresi ón] del Excel.

Abrimos el archivo Regresión lineal y nos vamos a la hoja Análisis de datos 1.

El uso de la secuencia [Datos] – [Análisis de datos] – [Regresión] nos lleva a la siguiente ventana que la completaremos como se indica en la figura.


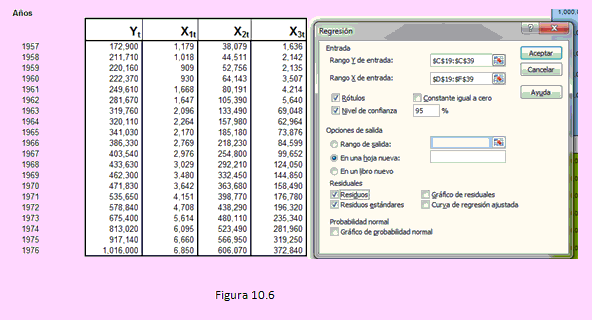
En esta figura tenemos los datos correspondientes a las variables producción agrícola (Y₁), volumen de fitosanitarios (X_1t), maquinaria agrícola (X_2t) y financiamiento público y privado (X_3t).

Aunque no es necesario para un análisis preliminar, le hemos pedido que nos emita en una hoja nueva, los residuales y los residuales estandarizados.

Luego de hacer clic en [Aceptar], obtendremos los resultados en una hoja nueva. Aquí sólo mostramos una parte. En la nueva hoja que ha creado se apreciará todos los resultados emitidos al usar la herramienta Regresión.



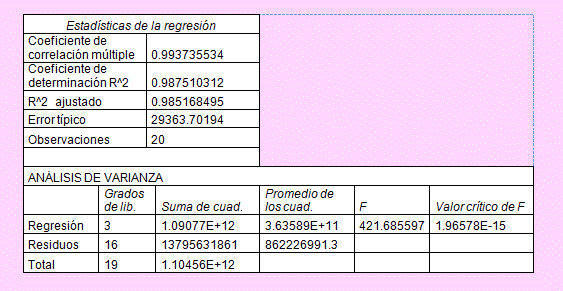
Al 5% de nivel de significación; es decir cuando el valor crítico es

F_<1-α(2,16) = 3.63373     y F_C = 421.685597, rechazaremos la hipótesis nula; en consecuencia, el modelo sí puede explicar el comportamiento de la producción agrícola.

El siguiente segmento de hoja corresponde a los resultados que nos permitirán realizar estimación por intervalos para los coeficientes de regresión así como prueba de hipótesis para cada coeficiente.



Intervalos del 95% de confianza:
En todos los casos t_1-α/2(n-k-1)= t_0.975(16)= 2.1199

Para βo:
Si el intervalo de confianza del 100(1-α)% para β_o es:



Para β₂ será:

-0.7070 – 2.1199 (0.2518) ≤ β₂ ≤-0.7070 + 2.1199 (0.2518)

Prueba de hipótesis para β₂

Ho: β₂ = 0. La producción agrícola no depende de la maquinaria agrícola
Ho: β₂ ≠ 0. La producción agrícola sí depende de la maquinaria agrícola

Estadístico de la prueba:

En la tercera fila y la cuarta columna encontramos el estadístico t_C = -2.8075

Como el valor crítico es t_1-α/2 (n-k-1)= t_0.975 (16)=2.11991

Entonces podemos rechazar la hipótesis nula; es decir, la producción agrícola sí depende de la maquinaria agrícola.

Ejemplo 03

En edición de la revista MacUser aparecieron los siguientes datos acerca de las características necesarias para que un usuario pueda seleccionar el monitor adecuado para su sistema de cómputo. Para las características de foco y brillantez, las calificaciones más altas indican mejor calidad. Para la falta de convergencia, distorsión y uniformidad, las calificaciones menores indican mejor calidad. Haga un análisis de los datos y realice una estimación lineal para determinar el precio del monitor.



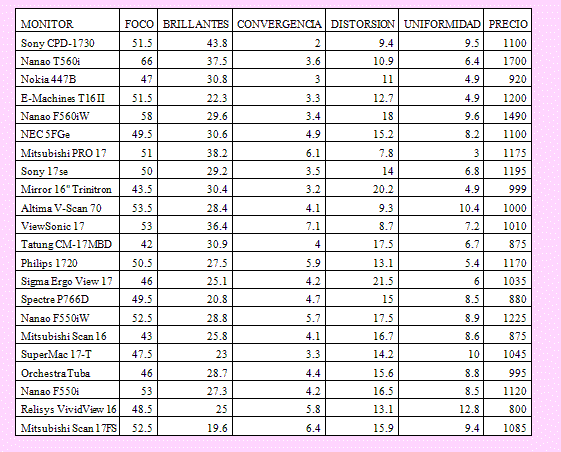
Solución

En este problema la variable dependiente es el precio del monitor. Puesto que se sospecha que esta variable dependa de las otras, nuestras hipótesis serán:
Ho: El modelo lineal no explica el precio
H1: El modelo lineal es el adecuado para explicar el comportamiento del precio

Introduciremos estos datos a una hoja del Excel.

El archivo RegreLinea.xlsx ya contiene los datos en su hoja Problema 2.

El rango de los datos de Precio se llama Precio, el rango de las variables independientes se llama Vardep. Estos nombres nos facilitaran su uso.

Usemos la secuencia: [Datos] - [An álisis de datos] - [Regresión] - [Aceptar] La ventana que se obtiene debemos completarla de la siguiente manera:



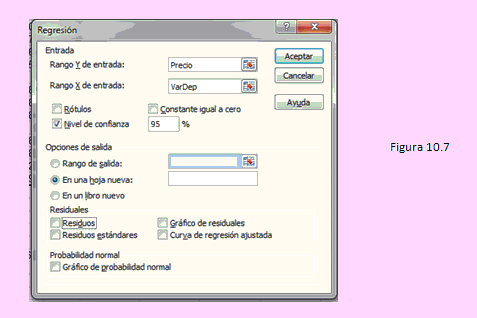
Luego de hacer clic en [aceptar] obtendremos los resultados en una hoja nueva.



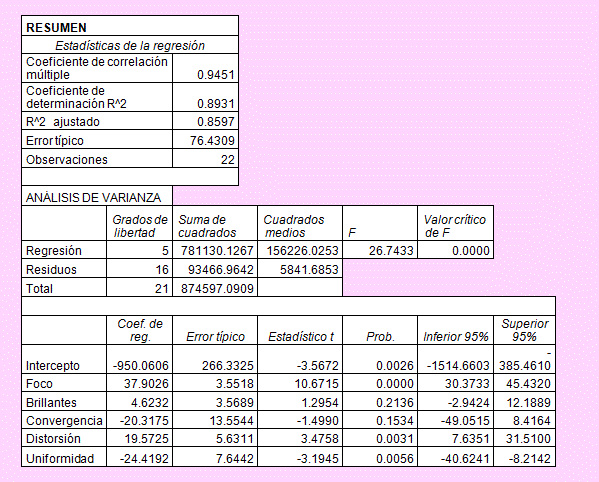
Según la tabla del ANOVA, F_C = 26.7433

El valor crítico para un nivel del 5% es: F_0.95 (5,16)= 2.85241

Según esto, rechazaremos la hipótesis nula; esto significa que el modelo es adecuado para explicar el comportamiento del precio del monitor.

Tomando en cuenta los estimadores de los coeficientes de regresión, el modelo estimado será:

Precio = -950.06 + 37.9026Foco + 4.6232Brillantes -20.3175Convergencia + 19.5725Distorsión – 24.4192Uniformidad

10.3 PROBLEMAS PROPUESTOS

1. Tico S.A. es una empresa que desea analizar el ingreso de los conductores de los vehículos tico, utilizado como taxi en los distritos y asentamientos humanos de la gran Lima. Para incrementar el ingreso de sus asociados decide realizar una campaña publicitaria utilizando todos los postes y paredes permitidos por la municipalidad de cada distrito. Los datos obtenidos en las observaciones realizadas en un período de 8 días se muestra en la siguiente tabla:

 

Ingreso diario	96	90	95	92	95	94	94	97
Gasto en publicidad	13.0	8.8	11.2	10.5	12.8	11.6	13.4	11.0

a) ¿Se puede afirmar que los gastos en publicidad favorecen a los ingresos diarios de los asociados?
b) Estime los coeficientes de la ecuación de regresión
c) ¿Cuál sería el ingreso de un asociado si se gastara 15 soles en publicidad?
d) ¿Cuál es el intervalo de confianza del 95% para βsub>1?

2. Extraído de la página 230 del libro Problemas de econometría de A. Aznar y A. García, que lo proponen como problema 3.20. En un intento de predecir la cotización del régimen general de la Seguridad Social en España para1980, se estimó un modelo Y = β₀ +β₁ X₁ + β₂ X₂ + ε_i donde Y es la base media trimestral, X₁ es el salario mínimo interprofesional y X₂ es la retribución medida por hora trabajada. Los datos con los que se desea estimar el modelo se presentan en la tabla de la hoja Cotización del archivo Regresión lineal.
a) Construya el modelo y diga si es un modelo significativo para este problema.
b) Obtenga intervalos de confianza del 95% para los coeficientes de regresión y realice prueba de hipótesis para cada uno de ellos.

3. Una empresa dedicada a la venta e instalación de productos de seguridad domiciliaria desea colocar sus productos en 10 ciudades del interior del país. El gerente de la empresa dispone de los datos históricos de otras empresas residentes en las 10 localidades. Estos datos se muestran en la hoja Seguridad del archivo Regresión lineal.
Los datos corresponden a los precios del producto de la competencia y la demanda potencial en cada ciudad, obtenida mediante un sondeo rápido de opinión.
a) Determine la ecuación de regresión que puede estimar las ventas a partir del precio de la competencia y la demanda potencial encontrada.
b) Interprete adecuadamente los coeficientes de regresión estimados.
c) ¿Cómo interpreta el coeficiente de determinación?
d) ¿Cuál será la venta estimada si el precio de venta más instalación es de 200 y la demanda potencial es de 160?

Siguiente sesión.