CAPÍTULO 6
ESTIMACIÓN DE PARÁMETROS
6.1 Introducción
6.2 Estimación puntual
6.3 Estimación por intervalos
6.4 Intervalo de confianza para la media
6.5 Intervalo de confianza para la proporción
6.6 Intervalo de confianza para la varianza
6.7 Intervalo de confianza para la razón de varianzas
6.8 Intervalo de confianza para la diferencia de medias
6.9 Intervalo de confianza para la diferencia de proporciones
6.10 Intervalo de confianza para datos pareados
6.11 Problemas propuestos
6.1 INTRODUCCIÓN
Todo el trabajo realizado en la etapa de muestreo y el cálculo de los estadísticos en la muestra, sirve para realizar un proceso de inferencia o estimación de los indicadores de la población a los cuales le llamamos parámetros.
Se ha realizado todo el trabajo previo con la única finalidad de conocer el comportamiento de la población la cual viene determinada por sus parámetros. De manera que, si éstos no son conocidos, deben ser estimados utilizando las herramientas de la teoría de la estimación de parámetros.
La estimación de un determinado parámetro puede ser realizada de dos maneras: tratando de estimar su valor a partir del valor de un estadístico o tratando de encontrar el valor del parámetro afirmando que éste se encuentra en un determinado intervalo.
Por ello en este capítulo se tomará en cuenta:
- La estimación puntual
- La estimación por intervalos
En la estimación puntual se tratará de estudiar las propiedades que debe tener un estadístico para ser un estimador y luego utilizar un determinado procedimiento o método para la obtención de un parámetro.
6.2 ESTIMACIÓN PUNTUAL
Definición
Sea X una variable aleatoria con f(x; θ), su función de distribución en el cual, θ representa el parámetro. Sea X1, X2, ... , Xn una muestra aleatoria de tamaño n, extraída de esta población. Diremos que  es un estimador del parámetro θ, si existe una función H tal que
es un estimador del parámetro θ, si existe una función H tal que  = H(X1 , X2 ,..., Xn ).
= H(X1 , X2 ,..., Xn ).
Si X1, X2, ..., Xn es una muestra aleatoria y H se aplica sobre ella, entonces el estimador  de θ es en realidad un estadístico de la muestra y H es la función que permite el cálculo de dicho estadístico.
de θ es en realidad un estadístico de la muestra y H es la función que permite el cálculo de dicho estadístico.

Según lo anterior, los estimadores se calculan.
Igualmente, la media muestral:  , la proporción muestral: p y la varianza muestral: s2, son estimadores de los correspondientes parámetros poblacionales: μ , π y σ2.
, la proporción muestral: p y la varianza muestral: s2, son estimadores de los correspondientes parámetros poblacionales: μ , π y σ2.
Luego

Siguiendo con la reflexión anterior, ¿es posible que de todos los posibles estimadores que pudiera tener un parámetro poblacional, habrá uno que es el mejor, el más eficiente, el que mejor lo describe y representa; es decir, el óptimo o el de mayor confianza?. En las siguientes secciones expondremos la respuesta a estas preguntas y veremos que si el parámetro puede tener varios estimadores, habrá uno que satisfaga mejor los requerimientos.
Propiedades de los estimadores
Para que sea un estimador de , debe poseer por lo menos una de las siguientes propiedades.
P1. Debe ser un estimador insesgado

¿Cuál es el estimador insesgado de π ?
El estimador insesgado de π es p.
Por qué?
Porque E(p) = π
En efecto: Puesto que
Como X → B(n, p) entonces E(X) = np, con lo cual E( ) = E(p) = np = π = θ
) = E(p) = np = π = θ
Observación:
Si Lim E( ) = θ , cuando n → ∞, entonces se dice que
) = θ , cuando n → ∞, entonces se dice que  es un estimador asintóticamente insesgado de θ.
es un estimador asintóticamente insesgado de θ.
Ejemplo 01

Ejemplo 02

Ejemplo 03

Recordemos que la sumatoria es igual a (n-1)s². Luego hemos multiplicado y dividido por ² para lograr dentro del paréntesis una variable Chi – cuadrado con (n-1) grados de libertad.
Como la esperanza de una Chi – cuadrado es (n-1),
Entonces E( ) = σ2 / n (n-1) = σ 2 - σ 2 / n.
) = σ2 / n (n-1) = σ 2 - σ 2 / n.
Lo que indica que  no es un estimador insesgado de σ 2. El sesgo es σ2/ n.
no es un estimador insesgado de σ 2. El sesgo es σ2/ n.
Y puesto que
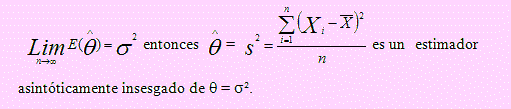
Ejemplo 04

Hemos multiplicado y dividido por (n - 1)σ2 para lograr dentro del paréntesis una variable Chi – cuadrado con (n-1) grados de libertad.
Como E(χ2(n-1)) = n-1
Luego E( ) = σ2(n - 1) / (n - 1) = σ2.
) = σ2(n - 1) / (n - 1) = σ2.
Observación:
Según a) y b) podemos concluir que σ2 tiene dos estimadores insesgados. ¿Cuál de ellos será el mejor?
La respuesta la daremos más adelante.
Ejemplo 05
De una población N(μ , σ2) se escogen dos muestras aleatorias independientes de tamaños n1 y n2. Sean  1 y
1 y  2 las medias de las muestras, y s21 y s22 las varianzas muestrales respectivas.
2 las medias de las muestras, y s21 y s22 las varianzas muestrales respectivas.

Tomando esperanza a la ecuación, tenemos

Ejemplo 06
Sean  1 y
1 y  2 las medias de dos muestras aleatorias independientes de tamaño n1 y n2 escogidas de una población con distribución de Poisson, de parámetro θ = λ,
2 las medias de dos muestras aleatorias independientes de tamaño n1 y n2 escogidas de una población con distribución de Poisson, de parámetro θ = λ,
a) Probar que la estadística  = (n1
= (n1 1 + n2
1 + n2 2) / (n1 + n2 ) es un estimador insesgado de λ
2) / (n1 + n2 ) es un estimador insesgado de λ
b) Pruebe que la varianza de este estimador es igual a λ /(n1 + n2 ).
Solución
Para que  sea un estimador insesgado de θ = λ se debe cumplir que E(
sea un estimador insesgado de θ = λ se debe cumplir que E( ) = θ = λ
) = θ = λ

P2. Debe ser un ESTIMADOR CONSISTENTE
Un estimador  es un estimador CONSISTENTE del parámetro θ si P(|
es un estimador CONSISTENTE del parámetro θ si P(|  - θ | > ε ) = 0
- θ | > ε ) = 0
Es decir, si la probabilidad de que la desviación entre el valor del estimador y el valor del parámetro sea mayor que un cierto valor, es insignificante. Se comprueba que  es un estimador consistente de θ si
es un estimador consistente de θ si

Ejemplo 07
¿Es  =
=  un estimador consistente de θ = μ?
un estimador consistente de θ = μ?
Solución
Usemos el procedimiento dado en la observación anterior.
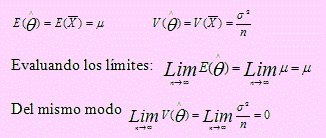
Según esto,  =
=  es un estimador consistente de θ = μ
es un estimador consistente de θ = μ
Ejemplo 08
Sea  = 1/3
= 1/3  1 + 2/3
1 + 2/3  2 un estimador de θ = μ. Demuestre que
2 un estimador de θ = μ. Demuestre que  es un estimador consistente de θ = μ .
es un estimador consistente de θ = μ .
Solución
Tomando esperanza:
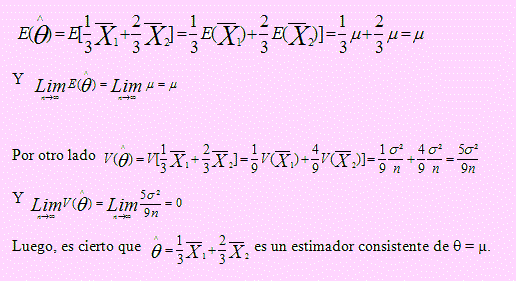
Ejemplo 09
Sea X1, X2, …, Xn una muestra aleatoria extraída de una población N(μ , σ2).

Como la segunda condición también se cumple, entonces s2 es un estimador consistente de σ2.
Seguiremos los mismos pasos que en a)
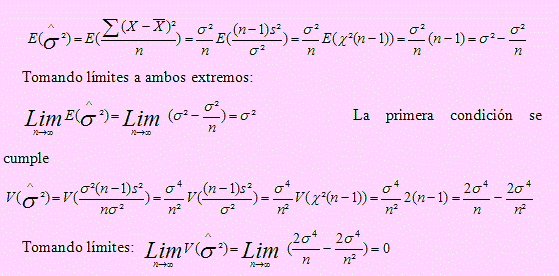
Luego  2 es un estimador consistente de σ2 (a pesar de no ser insesgado)
2 es un estimador consistente de σ2 (a pesar de no ser insesgado)
P3. Debe ser un ESTIMADOR EFICIENTE
Un estimador  es un estimador EFICIENTE del parámetro θ si es INSESGADO y de VARIANZA MINIMA.
es un estimador EFICIENTE del parámetro θ si es INSESGADO y de VARIANZA MINIMA.
Se dice que un estimador es de varianza mínima ya que si existiera otro estimador insesgado, digamos φ , entonces se debe cumplir que V( ) < V( φ ).
) < V( φ ).
Ejemplo 10
Sea X1, X2, X3, X4 , X5 una muestra aleatoria extraída de una población N(μ , σ2) y sean T1 y T2 las estadísticas
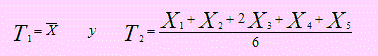
los estimadores de θ = μ . Alguno de ellos es un estimador más eficiente que el otro?
Solución
Paso1: Primero probaremos si son insesgados, encontrando E(T1) y E(T2 )
Paso 2: Obtendremos V(T1) y V(T2 )
Paso 3: Comparar las dos varianzas. La de menor varianza será el más eficiente.
En efecto: E(T1) = E( ) = μ
) = μ
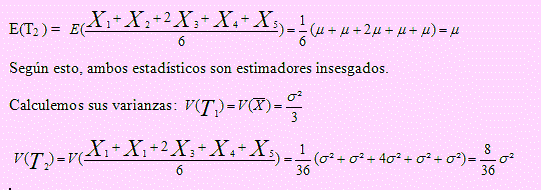
Se puede apreciar que T2 es un estimador más eficiente pues es insesgado y de menor varianza que T1.
Ejemplo 11
Sea X1, X2, X3, X4 una muestra aleatoria de cualquier población con μ y σ2 sus parámetros. ¿Cuál de los dos estadísticos que se definen a continuación, es el estimador de μ más eficiente?.

Ambos son insesgados? Sí son insesgados los dos estimadores.
Ahora debemos obtener la varianza de cada uno de ellos; es decir,
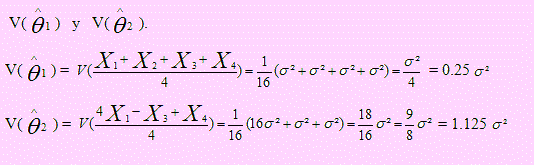
Luego el primer estimador es un estimador eficiente de μ ya que es insesgado y de varianza mínima.
Ejemplo 12
Sea X1, X2, X3 una muestra aleatoria de cualquier población con μ y σ2 = 1. De los siguientes estimadores de μ:
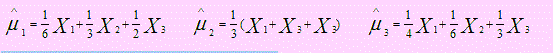
¿Cuáles son estimadores insesgados de μ?
¿Cuál es el estimador de varianza mínima?
Veamos si son insesgados:
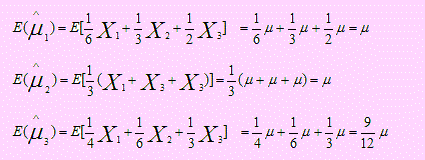
Los dos primeros son insesgados; por tanto calcularemos la varianza sólo de los que son insesgados:
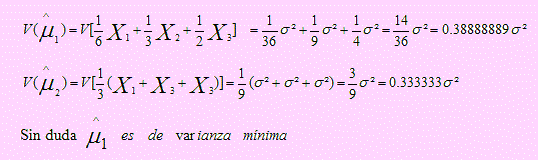
p4. Debe ser un estimador estadistico suficiente
Sea X1, X2, … , Xn una muestra aleatoria extraída de una población cuya función de densidad es f(X; θ) y sea t una estadística muestral tal que T = t(X1, X2, …, X2 ).
Recordemos que T = t(X1, X2, …, Xn ) es una estadística obtenida en la muestra y como tal, define el comportamiento de la muestra y un estimador obtenido a partir de esta estadística permite estimar el parámetro determinando por tanto, el comportamiento poblacional.

Naturalmente alguna de ellas será considerada un estimador de algún parámetro poblacional. Por tanto, si dicho estadístico contiene suficiente información acerca del parámetro poblacional a quién pretende estimarlo, diremos que es un estadístico suficiente.
Definición de Estadística suficiente.
Sea X1, X2, …, Xn una muestra aleatoria extraída de una población cuya función de densidad es f(X; θ) y sea t una estadística muestral tal que T = t(X1, X2, …, Xn ).
Diremos que T es un estadístico suficiente para θ sí y sólo sí, la distribución condicional de X, f(X1, X2, …, Xn ) dado T = t(X1, X2, …, Xn ) es independiente del parámetro θ; es decir, P(X = x / T = t ) = r(X1, X2, …, Xn ) que no depende de θ como sí ocurre con f(X; θ).
Teorema: Criterio de la factorización
Sea X1, X1, …, X1 una muestra aleatoria extraída de una población cuya función de densidad es f(X; θ). Una estadística T = t(X1, X2, …, Xn ) es suficiente para θ sí y sólo sí la función de densidad conjunta f(X1, X2, …, Xn; θ) puede ser factorizado como sigue: f(X1, X2, …, Xn; θ) = g(t(X1, X2, …, Xn )) h(X1, X2, …, Xn ) donde g depende de X1, X2, …, Xn y h es independiente de θ.
Ejemplo 13
Sea X1, X2, …, Xn una muestra aleatoria extraída de una población cuyo parámetro es λ.

Primera forma: Usemos la deficinición

Segunda forma: Usemos el teorema de la factorización
En este caso hallaremos primero la función de densidad conjunta y trataremos de descomponerla factorizándola en por lo menos dos factores, f(x;θ) = g(x; θ).h(x), uno de los cuales: h(x), debe ser independiente del parámetro en cuestión. Si es así, diremos que la estadística que forme parte de g(x; θ) constituirá una estadística suficiente de θ.
En efecto:

Ejemplo 14
Sea X1, X2, …, Xn una muestra aleatoria extraída de una población cuya función de densidad es f(x; θ) = θxθ-1, 0 < x < 1; θ > 0. Hallar una estadística suficiente para θ.
Solución
Usemos el teorema de la factorización.

Ejemplo 15
Sea X1, X2, …, Xn una muestra aleatoria extraída de una población cuya función de densidad es f(x; α) = αe-αx , 0 < x < 1; α > 0. Hallar una estadística suficiente para α.
Solución
Encontremos primero la distribución conjunta, f(X1, X2, …Xn; α)
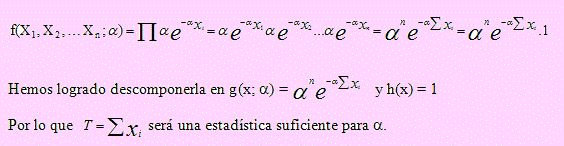
Métodos de obtención de estimadores
En el tema anterior nos hemos dedicado a verificar si un determinado estimador goza de una o más propiedades. Esto nos permitirá tomar la decisión de seleccionar el estimador que goza de la mayor cantidad de propiedades. Pero la gran pregunta que nos hacemos es: ¿Cómo obtener un estimador para un determinado parámetro? ¿Cómo o qué procedimiento debemos usar para encontrar un buen o el mejor estimador?.
Sin duda podríamos tomar una muestra y encontrar en ella uno o más estadísticos que puedan comportarse como verdaderos estimadores de algún parámetro. Esta podría una forma de encontrar estimadores. Otros procedimientos a ser utilizados son conocidos como los métodos para estimar los parámetros. En consecuencia, en esta sección nos ocuparemos del estudio de los diferentes métodos de estimación más conocidos.
Los métodos de estimación de estimación de parámetros más conocidos son:
Método de los Momentos
Método de Máxima Verosimilitud
Método de los Mínimos Cuadrados
Método de los momentos
Antes de presentar este método, definamos lo que son los momentos de una variable.
Definición de momento poblacional de una variable aleatoria
Los momentos de una distribución de variable continua son los valores esperados de las potencias de la variable; es decir, E(Xr). La potencia de la variable indica el “orden” o grado del momento.
Notación:
Usaremos μr para designar al momento poblacional de orden r de la variable.
Caso de una variable continua:
El momento poblacional de order r se define como
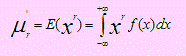
Observación:
El momento de orden 1, de X es µ’1 = E(X1) = E(X) = μ
El momento de orden 2, de X es: µ’2 = E(X2) = σ2) + μ 2. (recuerde que σ2 = V(X) = E(X2) – (E(x))2 , desde donde hemos despejado E(X2).
Si X → Exponencial (α), entonces
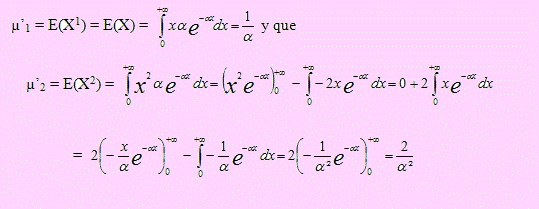
Nota 1:
Como σ2 = V(X) = E(X2) – (E(X) )2 entonces V(X) = μ’2 – (μ’1 )2
Nota 2:
Podríamos haber usado momentos para encontrar la media y varianza de cualquier variable aleatoria, sea uniforme, exponencial, normal, etc.
Caso de una variable discreta
El momento de orden “r” de una variable aleatoria discreta se define como
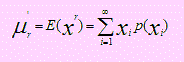
donde p(xi) es la función de distribución de X
Observación
Si X → Poisson(λ) entonces:
El momento de orden 1, de X es
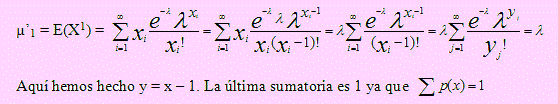
Usando el mismo procedimiento podríamos hallar el momento de orden 2 de esta variable y encontraríamos que E(X2 ) = λ2 + λ.
Momento muestral
Sea X1, X2, …, Xn una muestra aleatoria de tamaño n, extraída de una población de parámetro μ ; (esto es E(X) = μ). El momento muestral de orden r de la variable X, se define como
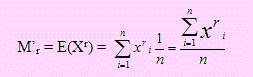
Hemos usado p(x) = 1/n ya que siendo una muestra aleatoria, cada uno de los elementos de la muestra tienen igual probabilidad de ser seleccionados.
Observación
El momento muestral de orden “1” de X es
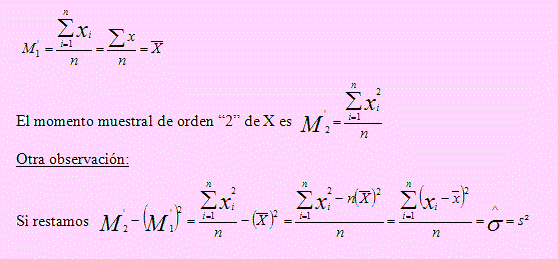
Es decir, el estimador asintóticamente insesgado de σ2 puede ser obtenido restando al momento de orden 2, el cuadrado del momento de orden 1, de X.
Estimación por el método de momentos
Sea f(x; θ1, θ2, …, θk) una función de densidad con k parámetros y sean μµ1, μµ2, … , μµ2 los primeros k momentos poblacionales. Sea X1, X2, …, Xn una muestra aleatoria extraída de la población anterior cuya función de densidad es f. Sean M’1, M’2, …, M’k son los primeros k momentos muestrales. Si θ2, θ2, ..., θk es la solución, en función de θ, de las k ecuaciones Mi = μi, i = 1, 2, …, k
Entonces diremos que dicha solución constituyen los estimadores obtenidos por el método de los momentos.
Procedimiento:
Obtener el primer momento poblacional y muestral. Igualando los dos resultados y despejando el parámetro, se tendrá el primer estimador.
Obtener el segundo momento poblacional y muestral. Igualando los dos resultados y despejando el parámetro en cuestión y usando el estimador del primer parámetro encontrado en el paso anterior, se tendrá el estimador del siguiente parámetro.
Continuar con el paso anterior hasta obtener el k – ésimo estimador.
Observación:
Si la población tiene r parámetros, se deberán obtener r estimadores; esto es, resolver r ecuaciones, usando los estimadores de los primeros parámetros.
Ejemplo 16
Sea X una variable aleatoria con función de densidad f(x; α) = αe-αx, x > 0; α > 0. Si X1, X2, …, Xn una muestra aleatoria extraída de la población, obtenga un estimador de α por el método de los momentos.
Solución
Puesto que la población dada sólo tiene un parámetro, = , deberemos resolver sólo una ecuación. Para ello empezamos obteniendo el primer momento muestral y poblacional:
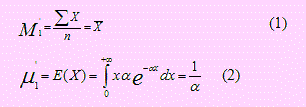
En realidad no era necesario integrar puesto que, siendo exponencial la función dada, por propiedades E(X) = 1/&alpha.
Ahora, formando la ecuación (1) = (2), obtenemos: α = 1/ , con lo cual podemos concluir que
, con lo cual podemos concluir que  = 1/
= 1/ es el estimador de α.
es el estimador de α.
Ejemplo 17
Dada la función de densidad poblacional f(x; α) = 2(α - x)/α2. Estímese α por el método de los momentos.
Solución

Observación:
Si la muestra fuera de tamaño 2, el estimador de α = 3(X1 + X2 + X3)/2
Ejemplo 18
Sea X1, X2, …, Xn una muestra aleatoria extraída de la población N(μ , σ 2) . Obtenga los estimadores de los parámetros µ y ² por el método de los momentos.
Solución
Puesto que la población posee dos parámetros, deberemos resolver dos ecuaciones: La primera;
Momento muestral de orden 1:

Estimación por el método de máxima verosimilitud
Función de verosimilitud
La Función de Verosimilitud de n variables aleatorias independientes X1, X2, …, Xn es la función de densidad conjunta de las n variables g(X1, X2, …, Xn; θ) . Esto es, si X1, X2, …, Xn es una muestra aleatoria extraída de una población cuya función de densidad es f , y su parámetro es θ, diremos que g(X1, X2, …, Xn; θ) constituye la Función de Verosimilitud de dichas variables.
En otras palabras:
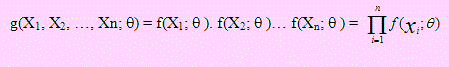
Observación:
Para hallar la función de verosimilitud de n variables es suficiente multiplicar n veces su función de densidad.
Ejemplo 19
Si X1, X2, …, Xn es una muestra aleatoria extraída de una población es exponencial, encuentre la función de verosimilitud para estas variables.
Solución
Si X1 → E(α), entonces
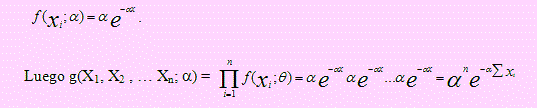
Nota:
Para simplificar las expresiones, si es posible, podríamos obviar el uso de los subíndices, como en la expresión anterior, pero siempre teniéndolos presente. Además, si usamos g(X1, X2 , … Xn; θ) podríamos simplificarlo por g(X; θ).
Ejemplo 20
Si X1, X2, …, Xn es una muestra de tamaño n, con Xi → N(µ, σ2), encuentre la función de verosimilitud para estas n variables.
Solución
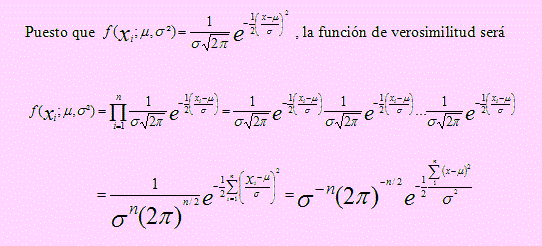
Ejemplo 21
Si X1, X2, …, Xn es una muestra aleatoria extraída de una población con función de densidad f(x; θ1, θ2) encuentre la función de verosimilitud para estas variables, donde
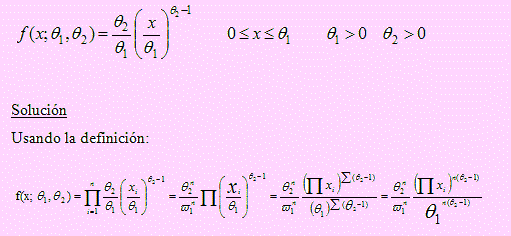
Estimador máximo -verosímil
Sea L(θ) = g(x1, x2, …, xn; θ) la función de verosimilitud para las variables x1, x2, …, xn. Si  = t(x1, x2, …, xn) es el valor de θ que maximiza a L(θ); es decir, L(
= t(x1, x2, …, xn) es el valor de θ que maximiza a L(θ); es decir, L( ) = Max {L(θ)}, diremos entonces que
) = Max {L(θ)}, diremos entonces que  = t(x1, x2, ..., xn) es el Estimador Máximo Verosímil de θ.
= t(x1, x2, ..., xn) es el Estimador Máximo Verosímil de θ.
Observaciones
Recordemos que, si f(x; θ) es la función de densidad poblacional y x1, x2, …, xn es una muestra aleatoria entonces L(x; θ) = f(x1; θ) f(x2; θ)… f(xn; θ0000)
Condición de regularidad: El estimador máximo verosímil (EMV) satisface la siguiente ecuación:

Para el caso de múltiples parámetros, en el caso de que se satisfaga las condiciones de regularidad, el punto en el cual L(x; ) es máxima es una solución del sistema:

Nota:
Procedimiento a seguir para obtener el Estimador Máximo Verosímil (EMV):
Paso 1: Obtener la función de verosimilitud L(X; θ)
Paso 2: Tomar Ln(L(X; )) y simplificar todo lo posible
Paso 3: Obtener las derivadas parciales respecto a cada parámetro
Paso 4: Igualar a cero las ecuaciones resultantes en el paso anterior
Cada una de las soluciones encontradas constituirá un EMV de θ.
Ejemplo 22
Si X1, X2, …, Xn es una muestra aleatoria extraída de una población es exponencial con f(x; α) su función de densidad, obtenga un estimador máximo verosímil para θ = α
Solución
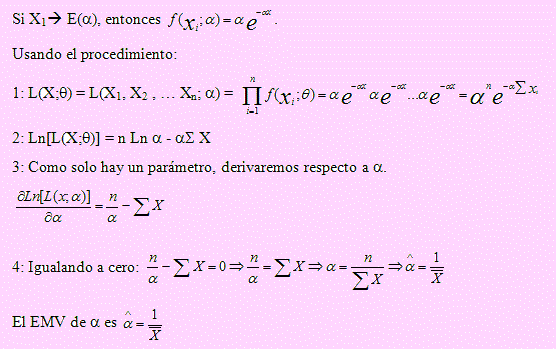
Ejemplo 23
Si X1, X2, …, Xn es una muestra de tamaño n, con Xi → N(μ , σ2), obtenga el EMV para μ y σ2.
Solución

Ejemplo 24
Si X1, X2, …, Xn es una muestra aleatoria extraída de una población con función de densidad f(x; θ1, θ2) tal que
f(x; θ1, θ2) tal que
= θ2 / θ1 (x/θ1)θ2 - 1, 0 le; x ≤ θ1, θ1 > 0, %theta; 2 > 0.
Hallar una estadística suficiente para θ = (θ1, θ2 )
Obtener el EMV para 1/θ2, suponiendo que θ1 es conocido.
Solución
Recordemos que para obtener una estadística suficiente para un parámetro debemos encontrar la función de distribución conjunta de X. Esta función es equivalente a encontrar la función de verosimilitud. Por lo que

Ejemplo 25
Si X1, X2, …, Xn es una muestra aleatoria extraída de una población poisoniana con función de densidad f(x; λ) = e-λxλx/x!.
Encuentre el EMV para λ.
Solución
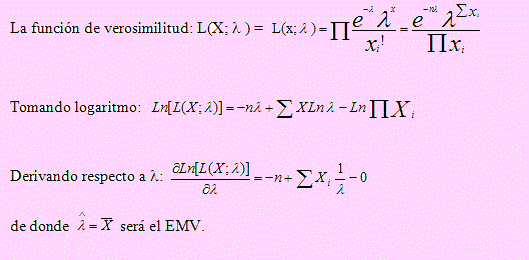
Ejemplo 26
Si X1, X2, …, Xn es una muestra aleatoria extraída de una población cuya función de densidad viene dada por f(x; θ) = θ( 1 + x)(-(1-θ), x > 0, θ > 0.
Hallar el estimador de θ por el método de los momentos, suponiendo que θ > 1
Hallar el EMV de 1/θ.
Solución

Estimación por el método de los mínimos cuadrados
Las poblaciones desde las cuales hemos extraído muestras aleatorias, presentan una distribución o función de densidad definida por una sola variable aleatoria. En base a ella, la teoría de la estimación puntual ha tratado de encontrar una estadística en la muestra capaz de ser usada como un estimador para cada uno de los parámetros de dicha población; esto es, los modelos poblacionales estudiados usan una sola variable.
Sin embargo, los modelos reales provienen de poblacionales con múltiples variables. Por ejemplo, si hablamos de la función de distribución de los ahorros de una familia, esta variable no sólo dependen de sus ingresos sino también de sus gastos, de su renta, de los impuestos que paga, etc.
De manera que el modelo general para este tipo de poblaciones, podríamos formularla como f(X1, X2, …, Xk; θ1, θ2, …, θk ; e) = 0 .
Una forma simplificada de este modelo puede ser expresado como Yi = g(X1i, X2i, …, Xki; θ2, …, θk ) + ei ; i = 1, 2, …, n donde la variable θ2, …, θk son los parámetros a ser estimados y ei son variables que deben satisfacer las siguientes condiciones:
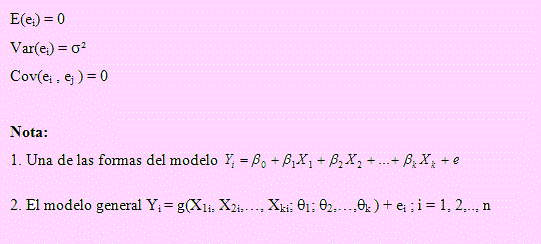
Estimador mínimo cuadrático

Paso 2: Derivar a esta sumatoria, respecto a cada uno de los parámetros e igualar a 0
Paso 3: Resolver el sistema de k ecuaciones
El conjunto de soluciones obtenidas, constituirán los valores de estimaciones mínimo cuadráticos de los respectivos parámetros.
Ejemplo 27
Sea Yi = A + BXi + ei el modelo lineal en donde Y constituye la variable explicada y X, la variable explicativa. Supongamos que X1, X2, ..., Xn es una muestra aleatoria extraída de esta población. Obtenga los EMC de los parámetros A y B.
Solución
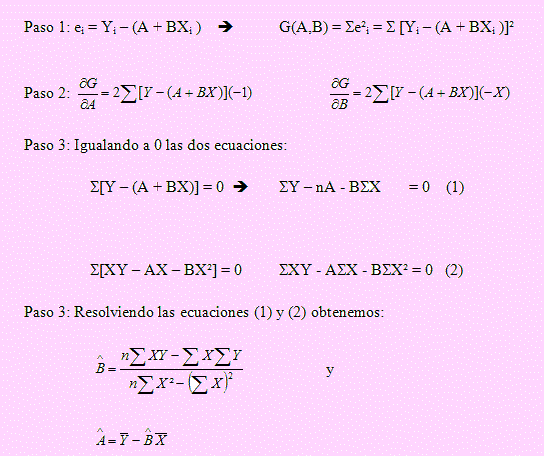
Que son los estimadores mínimo cuadráticos de Y = A + BX + e
Ejemplo 28
Supongamos que 8 ejemplares de cierto tipo de aleación fue producido en diferentes temperaturas y que se observó la durabilidad de cada ejemplar. La siguiente tabla muestra estos datos donde Xi representa la temperatura y Yi la durabilidad del i-ésimo ejemplar.
Ajustar una línea recta de la forma Y = α + βX + e a estos valores por el método de los mínimos cuadrados.
| i |
Xi |
Yi |
| 1 |
0.5 |
40 |
| 2 |
1 |
41 |
| 3 |
1.5 |
43 |
| 4 |
2 |
42 |
| 5 |
2.5 |
44 |
| 6 |
3 |
42 |
| 7 |
3.5 |
43 |
| 8 |
4 |
42 |
Ajustar una parábola de la forma Y = β0 + β1X + β2X2 + e &nbs´; a estos valores por el método de los mínimos cuadrados.
Solución
Usando la solución del ejemplo anterior, si Y = α + βX + e, entonces

Derivando respecto a cada parámetro, simplificando e igualando a cero:
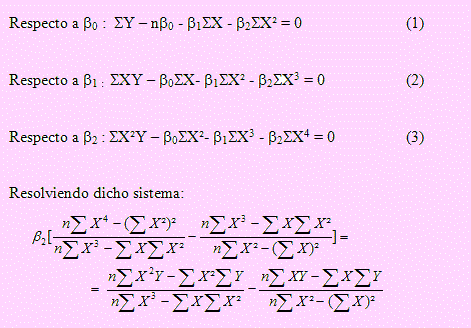
Sin despejar β2, reemplazamos las respectivas sumatorias y encontramos: β2 = -0.64285714
β1 = 3.44047619
β0 = 38.4821429
Con lo cual, la ecuación parabólica estimada es: Y = 38.482 + 3.441X – 0.643X2
Nota:
El archivo Solución Estimación puntual contiene muchos ejercicios resueltos.
6.3 ESTIMACIÓN POR INTERVALO
Por qué estimación por intervalo?
El estudio de la estimación puntual nos ha permitido analizar uno o más estadísticos de la forma T = t(X1, X2,…, Xn) y determinar si éste puede ser un buen estimador  de θ.
de θ.
Y gracias al fundamento teórico en el cual nos basamos para deducir que  es un estimador del parámetro θ, podemos inferir, deducir o aproximar un valor a dicho parámetro de manera que, sin conocer su verdadero valor, podemos aproximarnos a él con sólo encontrar el estadístico en la muestra, capaz de ser usado como su estimador.
es un estimador del parámetro θ, podemos inferir, deducir o aproximar un valor a dicho parámetro de manera que, sin conocer su verdadero valor, podemos aproximarnos a él con sólo encontrar el estadístico en la muestra, capaz de ser usado como su estimador.
Por ejemplo:
Si a una muestra de 40 trabajadores de la empresa CONSIL de 320 trabajadores se les pregunta por sus ingresos familiares y se encuentra que el ingreso medio en la muestra es de 1200 soles, la estimación puntual nos permitirá estimar el ingreso familiar promedio de todos los trabajadores y afirmar que dicho promedio es de 1200 soles.
En este caso, con n = 40, y  =1200, podemos esperar que todos los trabajadores de la empresa, tengan un ingreso familiar promedio de 1200 soles; esto es, μ = 1200 ya que
=1200, podemos esperar que todos los trabajadores de la empresa, tengan un ingreso familiar promedio de 1200 soles; esto es, μ = 1200 ya que  es un buen estimador de θ = μ porque es insesgado, es consistente y puede ser más eficiente que otros; es decir, E(
es un buen estimador de θ = μ porque es insesgado, es consistente y puede ser más eficiente que otros; es decir, E( )= μ=1200
)= μ=1200
Pero esta forma de estimar el promedio poblacional tiene un altísimo riesgo de no ser cierto.
Veamos la siguiente presentación abriendo el siguiente archivo y ejecutando la presentación.
El archivo es Intervalos.ppsx.
Después de haber observado y tomado nota las definiciones dadas en la presentación, si el estadístico  es el estimador de θ, el Intervalo de Confianza para θ se define como
es el estimador de θ, el Intervalo de Confianza para θ se define como


6.4 INTERVALO DE CONFIANZA PARA LA MEDIA
Si aplicamos lo dicho líneas arriba a la media poblacional, tendremos:
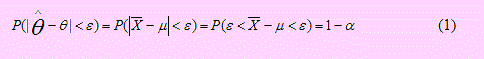
Cuando la varianza poblacional es conocida
El intervalo de confianza del 100(1 - α)% para μ será,  - ε ≤ θ ≤
- ε ≤ θ ≤  + ε (2)
+ ε (2)
En este intervalo sólo falta determinar el valor de ε. Esto lo haremos usando la distribución normal Z → N(0, 1) y puesto que la distribución muestral de  → N(μ σ2/n).
→ N(μ σ2/n).
Entonces

La siguiente figura muestra el Intervalo de confianza del 100(1-α)% para la Media
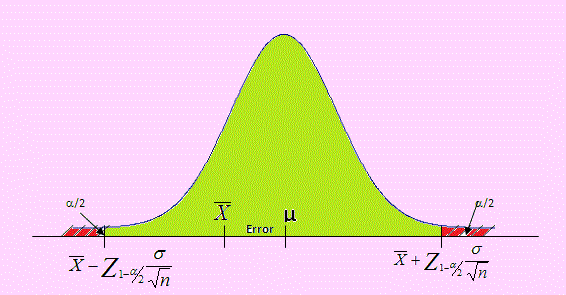
Nota importante:
Si el muestreo es sin reposición y el tamaño poblacional es finito, el intervalo será

Observación importante: Uso de MS EXCEL en la Estimación por Intervalos
El programa Excel no dispone de herramientas para resolver problemas de estimación por intervalos en el caso de la media cuando la varianza poblacional es conocida; es decir, cuando se debe usar la distribución normal. Sólo tiene para los casos en los cuales la varianza poblacional no es conocida.
Sin embargo, hemos implementado alguna rutina de cálculo de los intervalos de estimación para estos casos y como complemento para todos los caso de estimación por intervalo. Lo veremos más adelante. |
Estimación del tamaño de muestra

Esta fórmula supone que el muestreo se realiza con reposición o, si fuera sin reposición, la población se supone infinita o no se conoce, en cuyo caso se supone infinita. Por el contrario, si el muestreo se realiza sin reposición, que es lo usual y la población es finita, entonces

Nota:
Como es probable que no se conozca la varianza poblacional y no se tenga idea de su valor, se debe realizar una muestra piloto de 15 o 20 elementos, con lo cual, el punto de partida no será tan vago.
Ejemplo 29
Una máquina llena espárragos procesados en bolsas cuyo peso medio es μ gramos. Suponga que la población de los pesos es normal con σ = 20 gramos.
Si una muestra aleatoria de 16 bolsas ha dado una media de 495 gramos, Estime μ mediante un intervalo de confianza del 95%.
Solución
Puesto que la varianza poblacional es conocida, usaremos la distribución normal en donde el intervalo de confianza para μ es
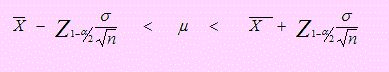
Por datos del problema tenemos:
n = 16;  = 495 ; 1 - α = 0.95; σ = 20
= 495 ; 1 - α = 0.95; σ = 20
Si 1 - α = 0.95 entonces α/2 = 0.025, con lo cual
Z(1-α⁄2) = Distr.Norm.Inv(0.025,0,1)= 1.96
Reemplazando todo esto en el intervalo dado encontraremos:
485.20 ≤ μ ≤ 504.80
Mediante Excel:
Abra el archivo Estimación por intervalos y vaya a la hoja IC Media 1. El segmento del lado izquierdo será usado para problemas de media cuando la varianza poblacional es conocida.
Como tenemos de datos la desviación estándar, ingresamos 20 en C7; la media muestral en C9; el tamaño de la muestra en C10 y el nivel de confianza en porcentaje en C11.
Luego de esto se puede apreciar, en la fila 20 tenemos la respuesta.
Ejemplo 30
Una gran preocupación del departamento psicopedagógico de un instituto militar es conocer los niveles de ansiedad de sus cadetes en el momento de rendir la última prueba que les permitirá el acceso al rango de oficiales. Se sabe que estos niveles en promociones pasadas ha tenido un promedio de 75 puntos con una desviación estándar de 10 puntos. Si se decide extraer una muestra de 100 cadetes y en ella se encuentra un nivel promedio de 70 puntos; ¿Cuál será el intervalo de confianza del 95% que nos permita estimar el nivel medio de ansiedad actual de todos los cadetes de la misma promoción?
Solución
Según los datos, σ = 10; μ = 75; n = 100; 1 – α = 0.95;  = 70.
= 70.
Si 1 – α = 0.95, entonces Z1 – α/2 = 1.96.
Con estos datos y reemplazándolos en la fórmula, el intervalo del 95% para μ es 68.04 ≤ μ ≤ 71.96
Luego podemos afirmar que el nivel medio de ansiedad de los cadetes de la promoción ha disminuido.
Mediante Excel
Como en el ejemplo 1, ingrese los datos en las celdas correspondientes de la hoja IC Media 1.
Ejemplo 31
Se desea estimar los montos impagos del año anterior en la municipalidad de san Juan de Lurigancho a fin de declarar una moratoria y puedan regularizar sus tributos. Se sabe que en el año anterior la desviación estándar de dichos montos fue S/. 35.
a) ¿Cuál será el tamaño de muestra necesario de contribuyentes, si se desea tener un margen de error no mayor a 8 soles, con una seguridad del 95%?
b) Si se sabe que el municipio tiene 25000 contribuyentes, ¿cuál será el tamaño de muestra necesario de contribuyentes, si se desea tener un margen de error de 5 soles con una seguridad del 95%?
Solución
Según los datos: σ = 35
a) 1 – α = 0.95; ε = 8;

Cuando la varianza poblacional es desconocida
En este caso debemos analizar dos situaciones:
i) Cuando el tamaño de muestra es menor o igual a 30; (n ≤ 30).
Según hemos visto en distribuciones muestrales de la media muestral, cuando se desconoce la varianza poblacional y se supone que la población desde donde se extrae la muestra es normal, la variable

ii) Cuando el tamaño de muestra es mayor que 30 (n > 30)
Se sabe que cuando el tamaño de muestra es mayor que 30, la distribución t de Student se aproxima a una distribución Normal N(0, 1) pues la población desde donde se extrae la muestra se supone normal. En este caso, el Intervalo de confianza para la media poblacional viene dado por
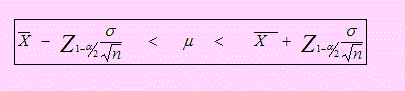
Nota:
Para la estimación del tamaño de muestra con varianza desconocida, se usará la varianza de la muestra como estimador puntual de la varianza poblacional y si no se conoce tampoco s2, se debe tomar una muestra piloto, tomando como n = 10 y calcular s2.
Ejemplo 32
Ilumina SA, fabrica focos cuya duración tiene una distribución normal. Si una muestra aleatoria de 9 focos da las siguientes vidas útiles en horas:
775, 780, 800, 795, 790, 785, 795, 780, 810.
Estimar la duración media de todos los focos del fabricante mediante un intervalo de confianza del 95%.
Solución
Se conoce σ²? ................. ....................... Tamaño de muestra? .............................
Qué distribución usamos? .............................. Por qué? ........................................
Recuerde entonces que en este caso debemos usar la distribución t de Student pues la varianza poblacional no es conocida.
Procedimiento:
Ingrese los datos a una hoja vacía del Excel, hacia la celdas: B2:B10
En B1 ingrese “Duración”
Seleccione el rango B1:B10, usando [Fórmulas]-[Crear desde la selección]-[Aceptar ]
En A12 ingrese “Media = “
En A13 ingrese “Varianza = “
En A14 ingrese “Desv. est.=”
En B12 ingrese la fórmula: =Promedio(Duración)
En B13 ingrese la fórmula: =Var(Duración)
En B14 ingrese la fórmula: =Raiz(B13)
En A15 ingrese “Valor de t”
En B15 ingrese la fórmula: =distr.t.inv(0.05,8)
Recuerde que el valor de t (9-1) y con un nivel de confianza del 95% es
t1-α/2 (n-1) = t0.975(8) =distr.t.inv(0.05,8) = 2.306
Usando  - t1-α/2(n-1) s/√n < μ <
- t1-α/2(n-1) s/√n < μ <  + t1-α/2(n-1) s/√n
+ t1-α/2(n-1) s/√n
Obtenemos:
781.406 ≤ μ ≤ 798.594
Abra el archivo Solución ejemplos para ver la solución. Del mismo modo puede abrir Estimación por intervalos y use el lado derecho de la hoja IC Media 1.
Ejemplo 33
Extraída una muestra de 30 cajas de un determinado producto de exportación, se midieron sus pesos y se obtuvieron los siguientes resultados:
| 250 |
275 |
287 |
298 |
307 |
322 |
| 265 |
277 |
289 |
301 |
309 |
324 |
| 267 |
281 |
291 |
303 |
311 |
328 |
| 269 |
283 |
293 |
306 |
315 |
335 |
| 271 |
284 |
293 |
307 |
319 |
339 |
Usando Intervalo de confianza, diga Usted si ésta muestra confirma la afirmación de que el peso medio de cada caja del lote debe ser de 300 Kg. Use α = 0.05
Sugerencia
Abra el archivo Solución ejemplos y vaya a la hoja Ejemplo 05.
Confirma o rechaza la afirmación? ..............................
Evidentemente, puesto que el peso medio de 300 Kg no está dentro del intervalo encontrado, no se confirma la afirmación.
Ejemplo 34
En una fábrica, al seleccionar una muestra de cierta pieza, se obtuvo las siguientes medidas para los diámetros de dichas piezas.

Estimar la media y varianza Construir el intervalo del 95% de confianza para la media
Sugerencia:
Ingrese los datos a una hoja del Excel y proceda como en el Ejemplo 03. Puede usar también el archivo Estimación por intervalos. Luego de calcular la media y desviación estándar de la muestra, puede usar el lado derecho de la hoja IC Media 1.
6.5 INTERVALO DE CONFIANZA PARA LA PROPORCIÓN
Sea X1, X2, …, Xn una muestra aleatoria extraída de n poblaciones Bernoulli en donde Xi = 0 ó 1; éxito o fracaso. Si X= ∑ Xi representa el número de éxitos en la muestra, entonces X %rarr; B(n,π) donde μ = nπ y σ2 = n<π(1-π).En este caso el parámetro es la proporción de éxitos, πpuesto que la población es Bernoulli, con p, la probabilidad de éxito y π = np . En una muestra aleatoria, el estadístico = debe ser un estimador de = π. De manera que el Intervalo de confianza para la proporción poblacional, π, proviene de

Observación importante
¿Cuál es el Intervalo de confianza de la proporción poblacional en los casos de muestreo sin reposición o si la población desde donde se extrae la muestra es finita?
Respuesta:

Ejemplo 35
Una compañía dedicada al estudio de encuestas de opinión, decidió realizar una encuesta sobre el voto en urna de una determinada población electoral. Para ello tomó una muestra aleatoria de 600 electores que terminaban de votar y encontró que 240 de ellos votaron a favor del candidato de la reelección.
a) Estimar el porcentaje de electores a favor de la reelección en toda la población, usando un nivel de confianza del 95%.
b) Si la proporción a favor de la reelección se estima en 40%, ¿cuánto es el error máximo de la estimación, si se quiere tener una confianza del 98%?
c) Si con la misma muestra la proporción a favor del candidato R se estima en 38% con una confianza del 98% de que el error no es mayor a 4.62%, ¿se puede proclamar al candidato a la reelección como ganador de la contienda?
d) Qué tan grande se requiere que sea el tamaño de otra muestra, si se desea tener una confianza del 94% de que el error de estimación de no sea superior al 2%?
Solución
Sea π: la proporción de electores a favor de la reelección
Y p: la proporción de electores a favor de la reelección en la muestra
Según los datos: n = 600; m = nro. de electores a favor de la reelección = 240, con lo cual diremos que p = 240/600 = 0.40
a) Como sabemos, el intervalo de confianza para una proporción (que asumimos infinita ya que N no es conocido) es
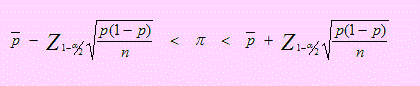
Como el nivel de confianza es del 98% , 1 - α/2 = 0.975 y Z1- α/2 = 1.96
Reemplazando estos datos y simplificando, tenemos:
0.3608 ≤ π ≤ 0.4392
Usando Excel
Abra el archivo Estimación por intervalos y vaya a la hoja IC proporción.
En D4 ingrese el tamaño de la muestra; en D5 ingrese el número de votos a favor (240) y en D7 ingrese el nivel de confianza (en porcentaje).
b) Como el nivel de confianza debe ser del 98%, entonces Z1 - α/2 = 2.32635
Si p = 0.40 y el Error de Estimación es ε = Z21-α7/2√(p(1-p)/n)
Reemplazando valores y simplificando tenemos: ε = 0.046527
En este caso el intervalo de confianza será: 0.40 – 0.0466 < π < 0.40 + 0.0466
Esto es 0.3534 ≤ π ≤ 0.4466
c) Para el candidato R, se tiene p = 0.38; n = 600; Z1 - α/2 = 2.32635; ε = 0.0462
El intervalo correspondiente será:
0.38 - 0.0462 <π< 0.38 + 0.0462 0.3338 ≤ π ≤ 0.4262
Puesto que la intersección de ambos intervalos no es nula, se dice que hay un empate técnico, ya que es probable que la estimación del parámetro en ambos casos, coincida.
d) En este caso para encontrar el tamaño de muestra usaremos la ecuación:
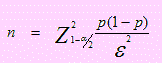
Como el nivel de confianza es el 94% entonces 1 - α/2 = 0.97 y Z1 - α/2 = 1.88079 ε = 0.02 y p = 0.4, de acuerdo a los datos del problema,
El tamaño de una nueva muestra será n = 2122
Nota:
Si no se usa el dato p = 0.4, entonces asumiríamos que p es desconocido, en cuyo caso, tomamos p = 0.5; con lo cual n = 2210.
Ejemplo 36
La empresa CromoTex está interesada en introducir un nuevo tipo de producto de acero en el mercado limeño. Para medir el nivel de aceptación de los potenciales consumidores, decide realizar un estudio de mercado a una población de 30,000 consumidores potenciales.
Qué tamaño de muestra deberá escoger si desea tener una confianza del 95% de que el error de la estimación de la proporción a favor del nuevo producto no sea superior al 4%?
Si con el tamaño de muestra calculado en a) se usa = 0.70 como estimación de la proporción de todos los consumidores que prefieren su producto. ¿Qué grado de confianza utilizó, si estimó de 19,783 a 22,217 el total de los consumidores de la población que prefieren su producto?
Solución
Según los datos: N = 30000; 1 - α/2 = 0.975 y Z1 - α/2 = 1.96; ε = 0.04; π = 0.5
¿El muestreo es con o sin reposición? Sin reposición
Según esto la fórmula para estimar el tamaño de muestra es:
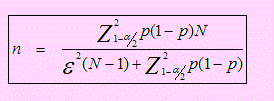
Reemplazando todos los datos y simplificando se tiene n = 589.
En Excel
Use la hoja n del archivo Tamaño de muestra general e introduzca los datos.
En cuanto a la segunda pregunta, donde p = 0.70,
Según el problema, si N es el total de la población, de los cuales el 70% está a favor del nuevo producto, el total de la población que está a favor del nuevo producto es Np; es decir, 30,000x0.70 = 21,000 habitantes.
Este total a favor del nuevo producto está en el intervalo 19,783 a 22,217.
Según esto, 19,783 < Np < 22,217.
Dividiendo entre N tenemos: 0.659433 ≤ p ≤ 0.7405667
Por otro lado, como el intervalo de confianza debe ser

Reemplazando en las dos ecuaciones: p = 0.70 y n = 589, con α desconocido, encontramos un Z1-α/2 = 2.1484.
Usando Excel, para encontrar 1 - α/2 , se debe usar =Distr.Norm(2.1484,0,1,1, lo que nos devuelve 0.984159.
Luego 1 - α/2 = 0.984159 de donde 1 – α = 0.938618; es decir, el nivel de confianza es del 96.83%.
Ejercicio 01
En un estudio socioeconómico se tomó una muestra aleatoria a 100 comerciantes informales de Gamarra y se encontró lo siguiente: un ingreso medio de $600, una desviación estándar de $50 y sólo el 30% de ellos tienen ingresos superiores a $800.
a) Estimar la proporción de todos los comerciantes con ingresos superiores a $800 usando para ello un intervalo del 98% de confianza.
b) Si la proporción de todos los comerciantes con ingresos superiores a $800 se estima entre 20.06% y 39.94%, qué grado de confianza se utilizó?
Sugerencia:
Usando la hoja IC proporción del archivo Estimación por intervalos, ingrese los datos para resolver la pregunta a). En cuanto a b) use el mismo procedimiento usado en el ejemplo anterior, igualando los extremos, como se hizo en (Eq.).
6.6 INTERVALO DE CONFIANZA PARA LA VARIANZA
¿Qué distribución muestral tiene el estadístico ? ............................
La respuesta es &xhi;2(n-1).
Puesto que debemos determinar el Intervalo de Confianza para una variable como T que tiene distribución Chi-Cuadrado, debemos encontrar un intervalo tal como se muestra en la siguiente figura:

El intervalo buscado será (K1, K2) tal que K1< T < K2 .
Se trata de encontrar los valore de K1 y K2 de tal forma que al reemplazar T por su definición, mostrada líneas arriba, podamos despejar σ2 y tener el intervalo para este parámetro.
Por otro lado, Si T → χ2(n-1) entonces K1 y K2 son valores χ2(n-1), tales que
K1 → χ2 α/2(n-1) y K2 → χ21-α/2(n-1)
Luego, el Intervalo de confianza del 100(1- α ) % para la varianza poblacional será:
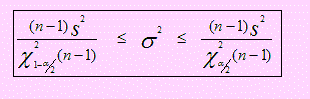
Trabajo de diseño de una plantilla
Observando cómo están preparadas las hojas del archivo Estimación por intervalos para obtener intervalos de confianza para la media y la proporción, inserte una nueva hoja y diseñe una plantilla que permita encontrar el intervalo de confianza para la varianza poblacional, dado el tamaño de muestra, la varianza muestral o desviación muestral y el nivel de confianza. Luego, usando esta nueva plantilla compruebe la solución del Ejemplo 37 |
Ejemplo 37
Se escoge una muestra aleatoria de 13 tiendas y se encuentra que las ventas de la semana de un determinado producto de consumo popular tiene una desviación estándar de s = 6 dólares. Si se supone que las ventas del producto tienen una distribución normal, estimar
a) la varianza poblacional
b) la desviación estándar poblacionalusando un intervalo de confianza del 95% en ambos casos.
Solución
Según los datos: n = 13; s = 6; 1 – α = 0.95
Qué distribución usamos para el IC de la varianza? La distribución Chi cuadrado.
El intervalo de confianza correspondiente viene dado por:
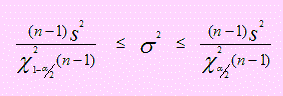
Abra el archivo Valor inv ChiCuadrado. Vaya a la hoja InvChiSquare [Ctrl]+i y use el método abreviado sugerido por el nombre de la hoja para ejecutar la macro y luego ingrese los valores que solicita.
Si 1 - α = 0.95, entonces χ21-α/2(13-1) = 23.397 y χ2α/2(13-1) = 4.3895.
a) Reemplace todos los valores en la fórmula y obtenga el intervalo para σ².
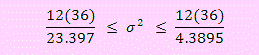
Luego el intervalo del 95% para la varianza es 18.4639 ≤ σ² ≤ 98.4167.
b) Extrayendo la raíz cuadrada al intervalo encontrado daremos respuesta. El intervalo de confianza del 95% para σ es 4.297 ≤ σ ≤ 9.921.
Ejemplo 38
Una máquina produce tubos de acero. Para estimar la variabilidad de los diámetros, se toma una muestra aleatoria de 10 piezas producidas por la máquina, encontrando los siguientes diámetros (en cms.):
10.1 9.7 10.3 10.4 9.9 9.8 9.9 10.1 10.3 9.9
Encuentre un intervalo de confianza del 95% para la varianza de los diámetros de todas las piezas producidas por la máquina. Suponga que los diámetros de las piezas se distribuyen normalmente.
Solución
Ingrese los datos a una hoja del Excel luego calcule la varianza usando la función =Var(RangoDeDatos). De esta forma, s² = 0.056.
Como 1 – α = 0.95 entonces χ21-α/2(10-1) = 20.4832 y χ2α/2(10-1) = 3.2469.
El intervalo de confianza del 95% para σ² será

6.7 INTERVALO DE CONFIANZA PARA LA RAZÓ DE VARIANZAS
Sean s12 y s22 las varianzas muestrales de dos muestras aleatorias e independientes de tamaño n1 y n2 seleccionadas desde dos poblaciones normales con varianzas σ12 y σ22 , respectivamente.
El estadístico  = s12 / s22 es un estimador de la razón de varianzas θ = σ12 / σ22
= s12 / s22 es un estimador de la razón de varianzas θ = σ12 / σ22
Nuestro interés consiste en encontrar un intervalo de confianza del 100(1-α)% para la razón de varianzas poblacionales a partir de P(|  - θ | < ε ) = 1 - α
- θ | < ε ) = 1 - α

Recuerde que:
No siendo simétrica esta distribución los valores de F son diferentes. El F de lado izquierdo de intervalo debe producir un F menor que el de la derecha.
Observe también cómo se deben tomar los grados de libertad y qué forma de cociente de varianzas se desea estimar.
Ejemplo 39
Una de las maneras de medir el grado de satisfacción de los empleados de una misma categoría en cuanto a la política salarial, es a través de las desviaciones estándar de sus salarios. La fábrica A afirma ser más homogénea en su política salarial que la fábrica B. Para verificar esa afirmación se escoge una muestra aleatoria de 10 empleados no especializados de A y 13 de B, obteniendo las dispersiones sA = 50 y sB = 30 de salario como mínimo. ¿Cuál sería su conclusión si utiliza un intervalo del 95% para el cociente de varianzas?. Suponga distribuciones normales.
Solución
Datos de la fábrica A: nA = 10; sA = 50
Datos de la fábrica B: nB= 13; sB = 30
Puesto que el problema consiste en obtener el intervalo de confianza del 95% para la razón de varianzas, usaremos la distribución F.
La afirmación planteada significa el uso de P(σA2 < σB2) , lo que significa que debemos usar como el intervalo para σA2 / σB2 . el intervalo a ser usado es

Ejemplo 40
Se sospecha que un laboratorio de medidas de viscosidad obtenidas en la mañana eran menores que en la tarde. Para confirmar esta sospecha, se toman dos muestras, una por la mañana y otra por la tarde, obteniéndose los siguientes resultados:
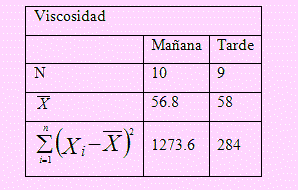
A un nivel del 95% de confianza, ¿existe suficiente evidencia estadística para afirmar que la variabilidad de la viscosidad difiere en ambos turnos?
Solución
Calculemos las varianzas muestrales de ambos turnos
sM2 = 1273.6/9 = 141.51111 sT2 = 284/8 = 35.5.
Use la hoja IC media 2 del archivo Estimación por intervalos.xlsm e ingrese los datos para obtener el intervalo pedido. La respuesta se da en el recuadro del lado derecho.
El intervalo del 95% para la razón de varianzas será
0.91485 ≤ σM2/σT2 ≤16.35133
Podemos afirmar que no hay suficiente evidencia para afirmar que la variabilidad de la viscosidad difiere.
6.8 INTERVALO DE CONFIANZA PARA LA DIFERENCIA DE MEDIAS
Sea  1 la media de una muestra de tamaño n1 extraída de una población normal y sea
1 la media de una muestra de tamaño n1 extraída de una población normal y sea  2 la media de una muestra de tamaño n2 extraída de otra población normal.
2 la media de una muestra de tamaño n2 extraída de otra población normal.
Hemos visto que  1 -
1 -  2 es una variable aleatoria definida como la diferencia de medias muestrales tales que, cuando se conoce las varianzas poblacionales entonces
2 es una variable aleatoria definida como la diferencia de medias muestrales tales que, cuando se conoce las varianzas poblacionales entonces

En consecuencia,
i) Cuando las varianzas poblacionales son conocidas
El intervalo de confianza para la diferencia de medias, μ1 - μ2 con el 100(1 – α)% será
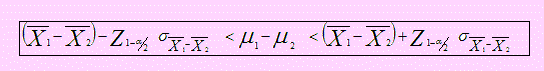
ii) Cuando las varianzas poblacionales no son conocidas
Debemos encontrar el intervalo de confianza para la razón de varianzas poblacionales.
Si este intervalo contiene al “1”; es decir, si las varianzas son homogéneas diremos que ambas son iguales y por tanto, usaremos la distribución t de Student tal que

donde v = n1 + n2 - 2 representa los grados de libertad.
Si el intervalo de confianza para la razón de varianzas no contiene al “1”; es decir se observa una diferencia entre ellas (no son homogéneas), entonces

Ejemplo 41
Para probar la efectividad de dos nuevas técnicas de ventas, se eligieron a dos grupos de vendedores. La primera técnica, aplicado a 18 vendedores, logró un promedio en sus ventas de 75 productos con una desviación de 5.
La segunda técnica se aplicó a 15 vendedores, quienes obtuvieron un promedio en sus ventas de 70 productos con una desviación de 6. Obtenga un intervalo de confianza del 95% para la diferencia de medias poblacionales. Hay diferencia significativa entre las dos técnicas?
Si hubiera, en términos del promedio de productos vendidos, ¿Cuál de ellas será la mejor?
Solución
Tomando en cuenta los datos del problema, completamos la siguiente tabla:
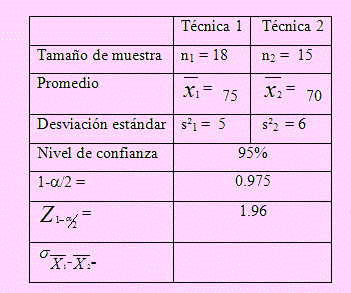
De acuerdo al problema, como las varianzas poblacionales son desconocidas, usaremos la distribución t de Student, pero para seleccionar la forma de evaluar la varianza de la diferencia de medias muestrales, σ2 1-
1- 2, debemos encontrar primero el intervalo de confianza para la razón o cociente de las varianzas poblacionales.
2, debemos encontrar primero el intervalo de confianza para la razón o cociente de las varianzas poblacionales.
Usaremos la hoja IC Media 2 del archivo Estimación por intervalos.
Introduciendo los datos como se muestra en el siguiente segmento de la hoja,
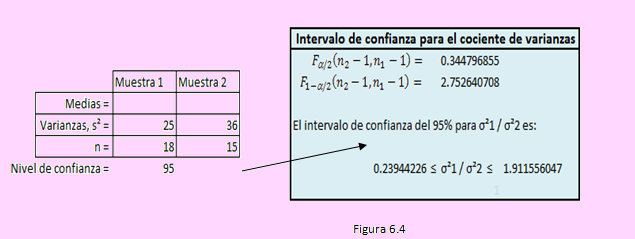
Según esto, podemos suponer varianzas poblacionales desconocidas pero iguales, ya que el intervalo de la razón contiene al “1”.
Ahora pasamos a introducir también las medias muestrales para obtener el intervalo de confianza del 95% para la diferencia de medias, lo que se muestra en la siguiente imagen:

Luego sí hay diferencia significativa entre las dos técnicas y en términos del promedio, la primera es mejor que la segunda.
Ejemplo 42
El banco del Estado de Río desea estimar la diferencia entre las medias de los saldos de las tarjetas de crédito de dos de sus sucursales. Una muestra independiente de tarjetahabientes generaron los resultados que aparecen en la siguiente tabla.

Hallar el estimador de la diferencia de medias de los saldos de las dos sucursales.
Hallarel intervalo de confianza del 99% para la diferencia de las medias de los saldos.
Solución
Al introducir estos datos a la planilla de la hoja IC Media 2, obtenemos la siguiente imagen:

Ante todo, el estimador de la diferencia de medias poblacionales es simplemente 500 – 375; es decir, $ 125.
Como el intervalo de confianza de la razón de varianzas indica, éstas son homogéneas. Por ello, el intervalo de confianza para la diferencia de medias se ha calculado usando la varianza de la diferencia de medias muestrales cuando las varianzas son iguales.
El intervalo hallado nos permite afirmar que el saldo promedio de dichas cuentas en la sucursal 1 es superior al de la sucursal 2.
Ejemplo 43
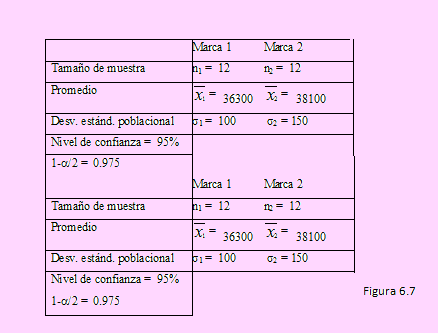
Una compañía de automóviles de alquiler está tratando de decidir la compra de neumáticos, entre las marcas GoodTrack y OptiRaid, para su flota de taxis en la ciudad. Para estimar la diferencia entre las dos marcas, se efectúa un experimento empleando 12 de cada marca. Los neumáticos se usan hasta que se desgastan. Los resultados para la muestra GoodTrack son:  1 = 36,300 Km; s1 = 100 Km. Para OptiRaid son
1 = 36,300 Km; s1 = 100 Km. Para OptiRaid son  2 = 38,100 Km y s2 = 150 Km.
2 = 38,100 Km y s2 = 150 Km.
Calcule un intervalo de confianza del 95% para μ1- μ2.
Suponga que las muestras son extraídas de una población aproximadamente normal. ¿Cuál de las dos marcas sugiere Ud.?
Solución
Completaremos la siguiente tabla con los datos del problema.
Introduciendo estos datos a la planilla de la hoja IC Media 2, obtenemos lo siguiente:

Como se puede apreciar, hemos usado varianzas desconocidas pero iguales, con lo cual podemos sugerir la compra de neumáticos OptiRaid.
6.9 INTERVALO DE CONFIANZA PARA LA DIFERENCIA DE PROPORCIONES
Sea X1, X2,..., Xn1 una muestra aleatoria extraída de una población Bernoulli. Sea X la variable Binomial definida como el número de éxitos en esta muestra y con parámetro π1, proporción poblacional de éxitos.
Sea Y1, Y2,..., Yn2 una muestra aleatoria extraída de una población Bernoulli. Sea Y la variable Binomial definida como el número de éxitos en esta muestra y tomemos a π2 como la proporción de éxitos en esta otra población. Supongamos que ambas muestras son independientes.
Si p1 y p2 son los estadísticos muestrales y definimos a  = p1-p2 como el estimador de la diferencia de proporciones poblacionales θ = π1-π2 entonces se debe cumplir que
= p1-p2 como el estimador de la diferencia de proporciones poblacionales θ = π1-π2 entonces se debe cumplir que

Nota:
Si n1 y n2 son bastante grandes el radical se calcula usando los estadísticos de la muestra; es decir, las proporciones muestrales.
Ejemplo 44
MillWard Brown, empresa investigadora de mercado es requerida para hacer un estudio sobre la preferencia de un producto. Se le pide que estime la proporción de hombres y mujeres que conocen el producto que está siendo promocionado en toda la ciudad.
En una muestra aleatoria de 100 hombres y 200 mujeres se determina que 20 hombres y 60 mujeres están familiarizados con el producto indicado. Construya un intervalo de confianza del 95% para la diferencia de proporciones de hombres y mujeres que conocen el producto. En base a estos resultados, ¿se estaría inclinado a concluir que existe una diferencia significativa entre las dos proporciones?
Solución
Sea π1 la proporción de mujeres que prefieren el producto.
Sea π2 la proporción de hombres que prefieren el producto.
Según los datos: Se trata de un problema de diferencia de proporciones. Los datos son:

Luego el intervalo de confianza del 95% será -0.0009 ≤ π1 – π2 ≤ 0.2009.
Según esto, existe diferencia significativa? . No hay diferencia significativa porque no se puede saber cuál de las proporciones es mayor.
Ejemplo 45
El gerente de control interno de una empresa le encarga a dos de sus técnicos, la verificación de la validez de un conjunto de certificados de ventas. Para ello se toma una muestra de 120 y se le distribuye 60 a cada uno de ellos.
Después de presentar su informe, se encuentra que el primer técnico examina a 40 y encuentra 10 falsos, mientras que el segundo técnico examina 50 y encuentra 15 falsos. Debido a la diferencia de entre estos porcentajes el gerente solicitó un intervalo de confianza del 95% para la diferencia de verdadera. ¿Este intervalo de confianza justificará la creencia del gerente de que los dos técnicos emplean métodos diferentes?
Solución
Según los datos, los tamaños de muestra reales son:
Primer técnico: n1 = 40; número de certificados falsos = 10
Segundo técnico: n2 = 50; número de certificados falsos = 15
Nivel de confianza = 1 – α = 0.95
Ingrese todos estos datos en las celdas correspondientes de la hoja IC proporción del archivo Estimación por intervalos.
Luego haga clic en el botón celeste pues se trata de la diferencia de proporciones.
Luego el intervalo de confianza del 95% para la diferencia de proporciones será
-0.2348 ≤ π1 – π2 ≤ 0.1348
Según este resultado, no existe diferencia significativa entre las proporciones de certificados hallados por ambos técnicos; es decir, no se justifica la creencia del gerente.
6.10 INTERVALO DE CONFIANZA PARA DATOS PAREADOS
Supongamos que a una muestra de tamaño n se le aplica un determinado “tratamiento” el cual puede consistir en evaluarlos, someterlos a una determinada acción, aplicarles un determinado medicamento, etc.
Supongamos que X1, X2,…, Xn constituye las medidas o valores de respuesta de la muestra antes de aplicarles el tratamiento. Del mismo modo, supongamos que Y1, Y2,…, Yn constituye las medidas o valores de respuesta de la muestra después de aplicarles dicho tratamiento.
br> Si estuviéramos interesados en analizar el efecto del tratamiento, es lógico definir otra variable Di = Xi – Yi o Di = Yi – Xi. El orden cómo se resta no interesa, interesa la interpretación correcta de la diferencia y lo que se quiere analizar.
Así las cosas podemos obtener estadísticas de la variable D como su media 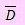 o su varianza muestral
o su varianza muestral

Nota:
Se debe tener cuidado de no confundir problemas de la media de datos pareados con problemas de diferencia de medias. En el primer caso se trata de una sola muestra sometida a dos formas de obtener resultados. En el segundo caso se tienen dos muestras muy precisadas y provenientes de dos poblaciones que poseen alguna forma de distribución.
Cómo encontrar un intervalo de confianza para la media de datos pareados:
Abra el archivo Estimación por intervalos y vaya a la hoja Datos pareados.
En ella ingrese los datos de X(Antes) e Y(Después), así como el nivel de confianza. De manera automática tendrá el intervalo de confianza para la media de datos pareados con el nivel de confianza indicado.
Ejemplo 46
Una empresa de software está investigando la utilidad de dos lenguajes diferentes para mejorar larapidez de programación. A doce programadores, familiarizados con ambos lenguajes, se les pide queprogramen un cierto algoritmo en ambos lenguajes, y se anota el tiempo que tardan, produciendo lossiguientes datos en minutos:
| VBA |
17 |
16 |
21 |
14 |
18 |
24 |
16 |
14 |
21 |
23 |
13 |
18 |
| Leng C |
18 |
14 |
19 |
11 |
23 |
21 |
10 |
13 |
19 |
24 |
15 |
20 |
Con base en estos datos, calcular:
a) Un intervalo de confianza al 95% para la diferencia de medias en el tiempo de programación.
b) ¿Puede considerarse que uno de los dos lenguajes es preferible al otro?”
Solución
Ingresemos los datos hacia las columnas A (Lenguaje 1) y B (Lenguaje 2) de la hoja Datos pareados del archivo Estimación por intervalos.
Al ingresar el nivel de confianza, obtendrá automáticamente los resultados estadísticos así como el intervalo de confianza para la media de los datos, lo que se muestra en la siguiente imagen:
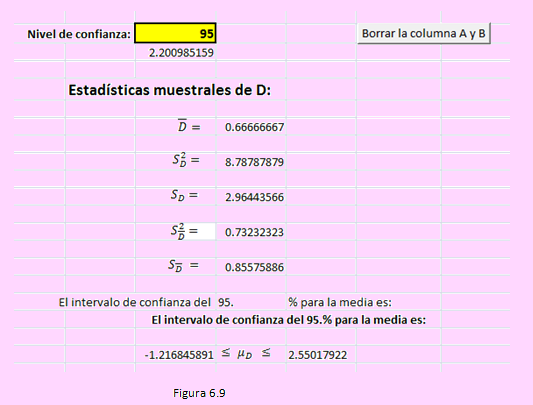
Podemos afirmar que no hay diferencia significativa en el beneficio de uno de esos lenguajes.
Ejemplo 47
Un analista financiero desea saber si ha habido o no cambio significativo en las utilidades por acción entre 2004 - 2005 de las empresas más grandes del país. Para tal efecto tomó una muestra de 10 empresas y obtuvo los siguientes resultados:
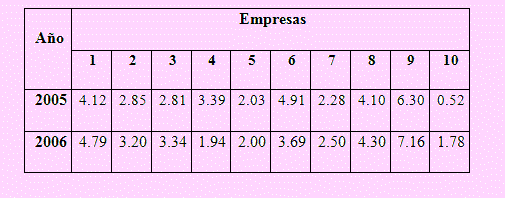
¿Con 98% de confianza, se puede afirmar que existe diferencia significativa en las utilidades entre estos dos años observados?
Solución
Ingrese los datos a la hoja Datos pareados del archivo arriba mencionado. Ingrese también el nivel de confianza de 98%.
Podemos concluir que no hay diferencia significativa en las utilidades netas de ambos años.
Los resultados se muestran en la siguiente imagen:

6.11 PROBLEMAS PROPUESTOS
Estimación de la media
1. Una tienda de pinturas quiere estimar la cantidad correcta de pintura que hay en las latas de un galón, compradas a un conocido fabricante. Por las especificaciones del productor se sabe que la desviación estándar de la cantidad de pintura es igual a 0.02 galones. Se selecciona una muestra aleatoria de 50 latas y se encuentra que la cantidad promedio de pintura en cada lata es 0.995 galones. Si la población desde donde se extra la muestra es normal. establezca una estimación por intervalo de confianza del 99% de la cantidad promedio real por lata de toda la producción.
Con base en estos resultados ¿sería posible que el propietario de la tienda tuviera derecho a quejarse al fabricante? ¿Por qué?
2. En los depósitos de la aduana se encuentran un total de 2000 equipos electrónicos requisados durante 10 años. El Jefe del almacén central estima el valor de todos estos productos en 30000 dólares. Con motivos de cambios en la dirección de la aduana se desea tener una estimación del valor promedio de todos estos productos. Para ello se tomó una aleatoria de 50 productos y se registraron sus valores x1, x2,. . ., x50, encontrándose:
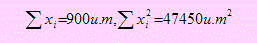
a) ¿Cuánto es el valor total estimado a partir de la muestra?
b) Utilizando un intervalo de confianza del 95% para el valor total, ¿es el valor estimado de la muestra coherente con el valor estimado por el Jefe de almacén? Verifique.
3. La Asociación Nacional de Defensa del Consumidor hace encuestas entre asiduos concurrentes a los chifas de Lima para determinar calificaciones de calidad de este tipo de restaurantes. La calificación máxima es de 10. Suponga que se toma una muestra aleatoria de 50 clientes y que a cada uno se le pide calificar al chifa Shao Ling. Las calificaciones obtenidas en la muestra se presentan en la columna A del archivo Probestimación.
¿Cuál es el intervalo de confianza del 95% para la calificación promedio de este chifa?
4. Con el fin de evaluar los pesos de las piezas producidas por cierta máquina se seleccionaron 30 piezas de la producción diaria de esta máquina:
250 265 267 269 271 275 277 281 283 284
287 289 291 293 293 298 301 303 306 307
307 309 311 315 319 322 324 328 335 339
Si el peso medio anterior era de 300 Kg, ¿podemos decir que dicho peso medio se mantiene o ha cambiado?
Estimación para la varianza
5. Para evaluar la eficiencia y rendimiento de un tipo de máquina en la producción de ciertas piezas, se toma en cuenta la cantidad de piezas producidas diariamente. Se registraron las cantidades de piezas producidas durante 30 días. La siguiente es la lista de la cantidad de piezas producidas diariamente.
10 11 11 11 12 12 12 12 13 13
13 13 13 13 13 13 13 13 13 13
14 14 14 14 14 15 15 15 16 16
a) Estime la media y la varianza de la cantidad de piezas producidas
b) ¿Cuál es el intervalo de confianza del 95% para la producción media?
c) ¿Cuál es el intervalo de confianza del 95% para la varianza de la producción diaria?
6. Según registros del departamento de calidad de la compañía “A”, el peso de ciertos paquetes de galletas tiene una distribución normal con peso medio de 40 gramos y una desviación estándar de 0.25 gramos. En una muestra aleatoria de 20 paquetes se encontró una desviación estándar de 0.32 gramos. ¿Con 95% de confianza, se podría concluir que la variabilidad de los paquetes se ha incrementado? Justifique su respuesta.
7. Sea X una variable aleatoria tal que X → N(μ, σ² ). Una muestra de tamaño 15 dio los siguientes estadísticos para X.

Determine un intervalo de confianza del 95% para la varianza poblacional.
Estimación de la proporción
8. Se desea realizar una encuesta de mercado para estimar la proporción de consumidores que prefieren a una de las dos marcas líderes en el mercado de embutidos. Asimismo, se requiere que el error al estimar esta proporción no sea mayor de 4 puntos porcentuales con un nivel de confianza del 95%. El Dpto. de marketing estima que el 25% de los consumidores prefieren a una de las marcas. Si cuesta US $1500 poner en marcha la encuesta y US $5 por entrevista, ¿cuál será el costo total de la encuesta?.
9. Vista Com S.A. desea estimar la proporción de sus clientes que comprarían una revista con los programas selectos de televisión por cable. La compañía emplea una confianza del 95% para un margen de error de 0.05 con respecto a la proporción real. La experiencia anterior en otras áreas señala que el 75% de los clientes comprarán la revista de programas. ¿Qué tamaño de muestra se necesita?
10. Marca Asociados, empresa de estudios de mercado, está interesada en conocer la proporción de consumidores de cierto producto cuya publicidad se lanzó hace dos meses. Si de una muestra de 300 personas, 100 consumen el producto.
a) ¿Cuál será el intervalo del 96% de confianza de la verdadera proporción de consumidores?
b) ¿Cuál que debería ser el tamaño de muestra en una posterior investigación, si se desea tener un nivel de confianza del 96% con un error de estimación no mayor a 0.04?.
Estimación de la Razón de varianzas y de diferencia de medias
11. Un agente de compras de una compañía se vio confrontado con dos tipos de máquinas dedicadas a la elaboración de cierto material audiovisual. Para decidirse por una de las dos máquinas el agente tuvo la oportunidad de probar ambas máquinas durante un determinado número de pruebas. Para ello se seleccionaron dos muestras para detectar la máquina de mayor rendimiento. Se eligieron 30 tareas de la primera máquina y 20 de la otra máquina y se obtuvieron los siguientes resultados:
En la primera máquina: Una media de 30 horas con una varianza de 135 horas².
En la segunda máquina: Una media de 20 horas con una varianza de 80 horas².
Encuentre el intervalo de confianza del 95% para la diferencia en el rendimiento promedio y diga cuál de las dos máquinas compraría el agente.
12. Una empresa posee un departamento de costos que informa del costo total soportado por la empresa y un departamento de ventas que informa de los ingresos totales. Los directivos desean conocer un rango de valores para el beneficio medio, con el fin de informar a los accionistas en la próxima Junta General. Ambos departamentos le proporcionan los datos que aparecen en las columnas B y C del archivo Prob estimación.
Sabiendo que los ingresos totales siguen una distribución normal con σ = 8 y los costos totales una distribución normal con σ = 10. Obtenga un intervalo de confianza del 99% para el beneficio medio.
13. La siguiente información se refiere a la vida útil en años de dos marcas de motores para refrigeradores:
| Marca |
Promedio |
Desv est. |
Muestra |
| A |
12.0 |
1.2 |
50 |
| B |
13.8 |
1.5 |
50 |
Si se calcula los límites de confianza del 90% para μA - &mu:B, ¿a qué conclusión llegaría usted?
Estimación de la diferencia de proporciones
14. En un instituto de idiomas se están probando dos nuevos métodos de enseñanza del inglés. Con el objeto de conocer sus resultados, en el método A se involucraron a 80 alumnos; mientras que 100 en el método B. Al final del ciclo académico se obtuvo que el 70% de los alumnos del método A fueron sobresalientes; en cambio en el método B, sólo al 60% se les pudo considerar como sobresalientes. Halle el intervalo de confianza del 99% para la verdadera diferencia en las proporciones de alumnos sobresalientes de los dos métodos de enseñanza del idioma inglés?
15. Una empresa de Marketing la semana pasada lanzó, por todos los medios de comunicación, la publicidad de un nuevo producto para el cuidado del cabello y quiere conocer si la publicidad permitió que el producto sea conocido, y sobre todo está interesada en saber si existe una diferencia marcada entre hombres y mujeres. Se tomó una muestra de 200 hombres de los cuales 80 contestaron que conocían el producto mientras que de una muestra de 200 mujeres la mitad dijeron conocer el producto, ¿cuál es el intervalo del 95% de confianza para la diferencia las proporciones entre hombres y mujeres?
Problemas Diversos
16. TransportSA afirma que el parque automotor de servicio público tiene una antigüedad promedio de 10 años. Para comprobar esta aseveración, se escogen al azar 400 unidades que circulan por la ciudad y se registra el número de años que están operando cada una de ellas. Se obtuvo los siguientes datos:
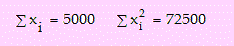
además se observó 80 unidades con una antigüedad mayor a 18 años
Calculando los límites de confianza del 95%, ¿encuentra apoyo la afirmación de la oficina de transportes?.
Estime con 98% de confianza la proporción de unidades con antigüedad no mayor a 18 años. Interprete su resultado.
17. A manera experimental, MutualSA entregado, previa evaluación, tarjetas de crédito a una muestra representativa de 20 trabajadores textiles, luego de un mes se registra el consumo, en soles, de cada uno de ellos con la mencionada tarjeta. Los datos obtenidos son:
68 76 63 77 87 63 64 83 76 67
66 62 76 79 58 73 66 69 64 51
Estime con 97% de confianza el consumo promedio real mensual de los empleados que hacen uso de esta tarjeta. Interprete el resultado obtenido.
Si el banco espera entregar en el futuro esta tarjeta a N = 2000 empleados textiles de la zona, estime con 97% de confianza el ingreso total del banco por consumos con esta tarjeta.
18. En un proceso de llenado de bolsas de detergentes se utiliza dos máquinas envasadoras. De acuerdo con las especificaciones técnicas, ambas maquinas deben llenar las bolsas con un contenido medio de 400 gm. El gerente de producción desea saber si en realidad no existe diferencia significativa entre ambas máquinas en el proceso de envasado. En tal sentido, selecciona al azar 10 bolsas de detergente producidos por una máquina y observó que el contenido medio fue de 403.34 gm. con una desviación estándar de 2.4 gm. Del mismo modo, escogió aleatoriamente 9 bolsas de la otra máquina, comprobando que el contenido medio de estos fue de 398.75 gm. con una desviación de 6.8 gm. ¿Cree usted que tiene sustento la afirmación del gerente de producción, si éste asume un nivel de confianza del 99%?
19. En la encuesta de estudio de mercado de un nuevo producto, se comprobó que a 150 de 250 consumidores potenciales entrevistados, no les agradó el producto. Además, se comprobó que en los consumidores a quienes les agradó el café, la edad promedio fue de 55 años con una desviación estándar de 25 años. Con una confianza del 95%:
a) ¿Entre que valores se podría estimar la proporción de los consumidores que les agrada el nuevo producto?
b) ¿Entre que valores se podría estimar la edad promedio de los consumidores que les agrada el nuevo producto?
20. El director de personal de una gran corporación quiere estudiar el ausentismo entre los empleados en las oficinas centrales de la empresa durante el último año. Una muestra aleatoria de 25 empleados mostró lo siguiente: una media de 9.7 días y una desviación estándar de 4.0 días; y 12 empleados estuvieron ausentes durante más de 10 días. Estime intervalos de confianza del 95% para cada uno de los casos siguientes:
a) El número promedio de días de ausentismo de los empleados durante el último año. Interprete.
b) La proporción de empleados ausentes más de 10 días en el último año.
c) ¿Qué tamaño de muestra requeriría si quisiera tener una confianza del 95% de estar en lo correcto en una escala de 1.5 días y se supone que la desviación estándar de la población es 4.5 días?
d) ¿Qué tamaño de muestra se necesitaría si el director deseara tener una confianza del 90% de estar en lo correcto en una escala de 0.075 de la proporción real de empleados que se ausentaron más de 10 días, si no se cuenta con estimados anteriores?
Siguiente sesión.
 es un estimador del parámetro θ, si existe una función H tal que
es un estimador del parámetro θ, si existe una función H tal que  = H(X1 , X2 ,..., Xn ).
= H(X1 , X2 ,..., Xn ). de θ es en realidad un estadístico de la muestra y H es la función que permite el cálculo de dicho estadístico.
de θ es en realidad un estadístico de la muestra y H es la función que permite el cálculo de dicho estadístico.
 , la proporción muestral: p y la varianza muestral: s2, son estimadores de los correspondientes parámetros poblacionales: μ , π y σ2.
, la proporción muestral: p y la varianza muestral: s2, son estimadores de los correspondientes parámetros poblacionales: μ , π y σ2.










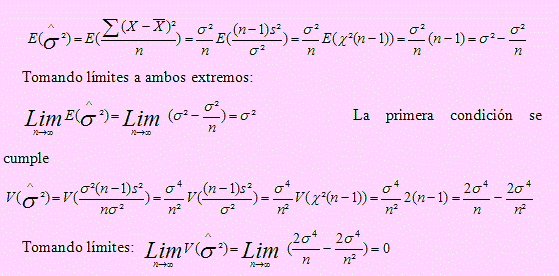
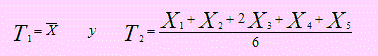
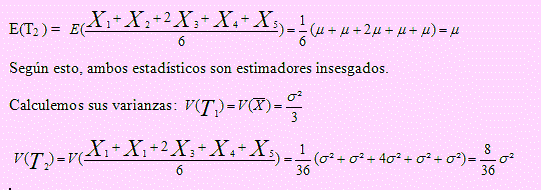

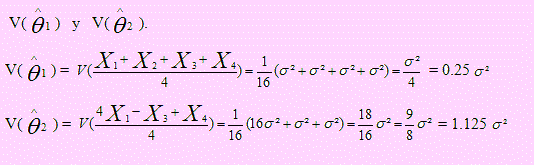
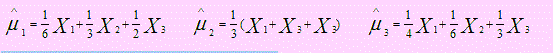
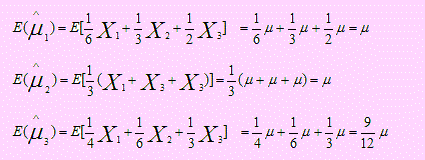
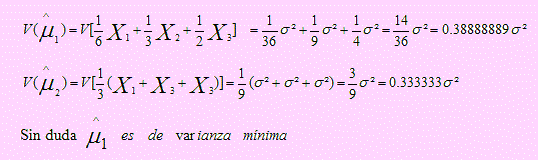




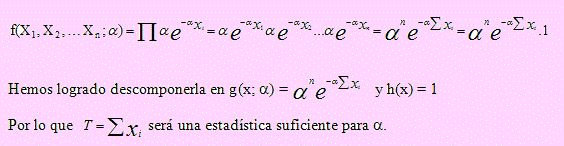
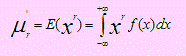
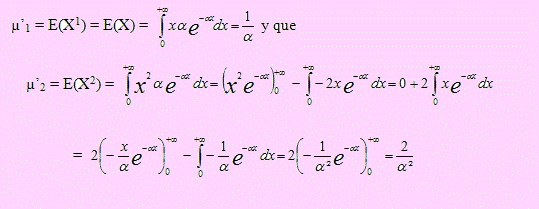
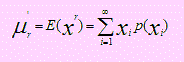
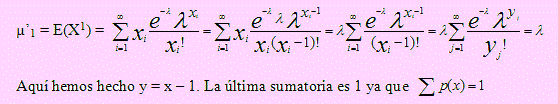
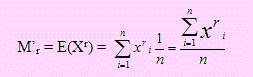
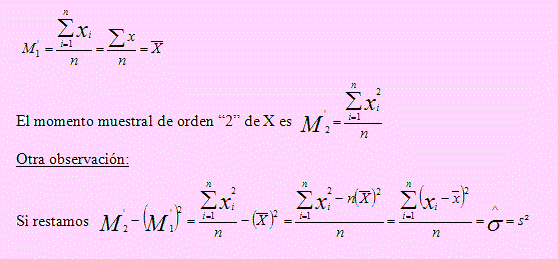
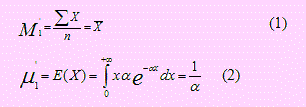


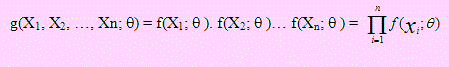
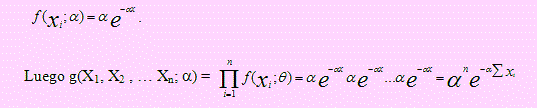
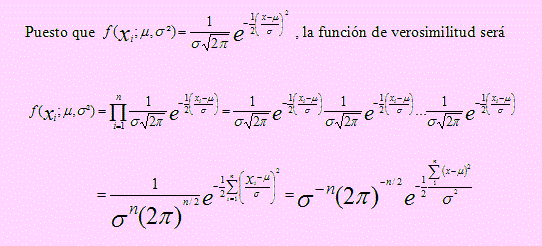
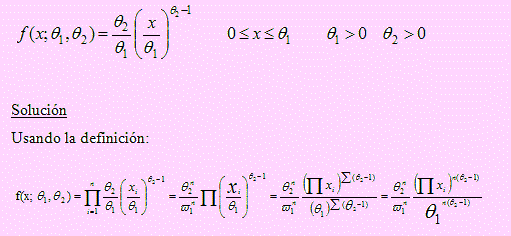


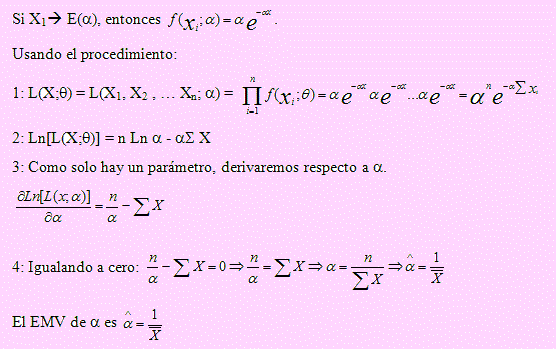


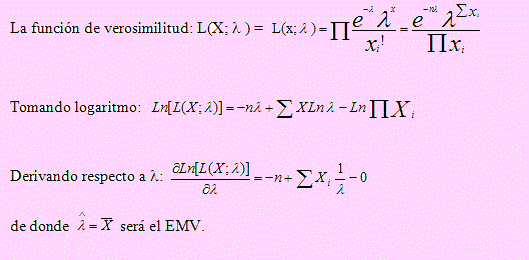

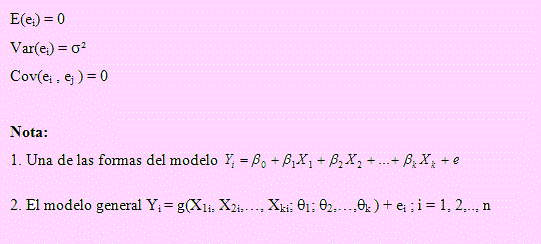

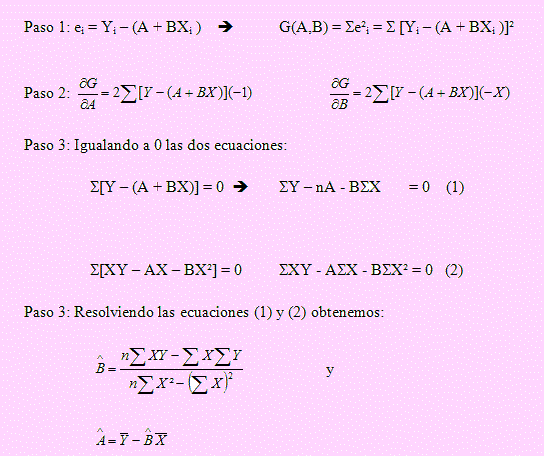

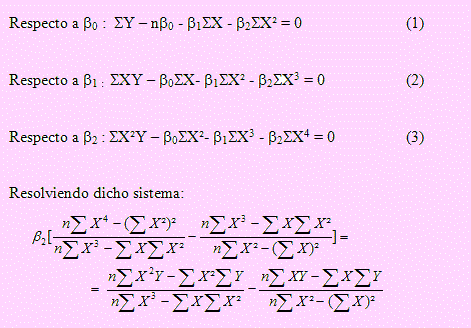


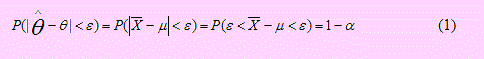





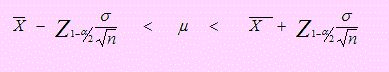


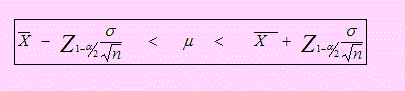



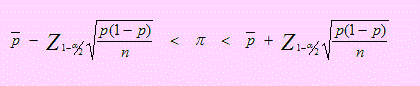
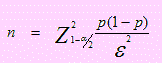
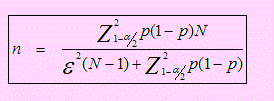


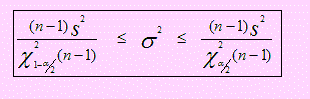
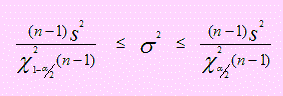
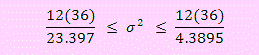





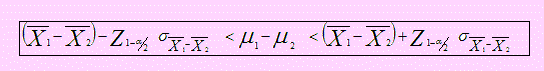











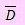 o su varianza muestral
o su varianza muestral