CAPÍTULO 8

DISEÑO DE EXPERIMENTOS

8.1 Conceptos básicos de Diseño de experimentos
8.2 Modelo de clasificación de una variable
8.3 Modelo de clasificación de dos variables
8.4 Problemas propuestos

8.1 CONCEPTOS BÁSICOS EN EL DISEÑO DE EXPERIMENTOS

Concepto de diseño de experimento:

El diseño de experimentos es una metodología estadística que, aplicada a un problema, requiere de una secuencia adecuada de pasos planeada (diseñada) previamente que nos permitan contar con los datos apropiados de modo que el análisis sea objetivo, claro y práctico a fin de establecer deducciones válidas respecto al problema en cuestión.

Veamos el siguiente ejemplo:

Un conjunto de trabajadores de una empresa es sometido a un curso de capacitación en el que deben pasar por cuatro módulos para adquirir la certificación el cual le permite acceder a una vacante de mayores ingresos. En el curso participan los trabajadores de los tres niveles que tiene la empresa. El número de trabajadores varones que participan es nH y el de mujeres es nM. Al final del curso la gerencia de recursos humanos recibe los resultados (número de participantes con certificación en cada módulo) que se muestran en la siguiente tabla.



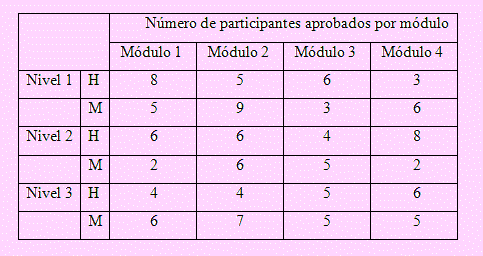
Frente a estos resultados Recursos Humanos se encuentra interesada en realizar una serie de comparaciones como por ejemplo: ¿Existe diferencia significativa en el rendimiento promedio entre los módulos? ¿Existe alguna diferencia significativa en rendimiento medio de los trabajadores de cada nivel? ¿Existe diferencia significativa en el rendimiento por género en cada módulo y en cada sucursal?

Todas estas preguntas significan elaborar pruebas de hipótesis de comparación de promedios en el cual se deben tomar en cuenta diferentes tipos de variables.

Distinguimos:

Variables independientes: Número de participantes aprobados por cada módulo.
Variables dependientes (endógenas): Número de participantes aprobados de cada nivel. Los valores de esta variable dependen fundamentalmente del nivel alque pertenece cada trabajador. Estas variables son explicadas por las variables independientes.
Variables exógenas: Aquellas cuyo aporte no son significativas en el modelo, como edad, estado civil, etc.
Tratamiento: Son la llamadas variables independientes, aquellas que deben ser controladas por el investigador.
Unidad experimental: Es el mínimo elemento al que se aplica el tratamiento. En este caso es un trabajador.
Diseño experimental completamente aleatorizado: Es aquel modelo en el cual los trabajadores son seleccionados aleatoriamente sin distinguir nivel ni género. Sólo se toma en el número de participantes con certificación por módulo. Diseño experimental en bloques completamente aleatorizado: Es el modelo en el cual las unidades experimentales son asignadas aleatoriamente en cada nivel de tratamiento constituyendo cada uno de ellos un bloque.
Análisis de varianza: Procedimiento estadístico que permite desagregar la variabilidad de la variable del problema tomando en cuenta la variabilidad de los resultados entre los tratamientos, dentro de cada uno de ellos, la variabilidad de los resultados por bloques y la variabilidad de los resultados en la interacción de bloques y tratamientos.

8.2 MODELO DE CLASIFICACIÓN DE UNA VARIABLE

El ejemplo anterior sugiere un modelo de dos variables con replicación pues estaríamos hablando de dos variables (por el lado de los tratamientos (módulos) y los bloques (niveles) y es con replicación porque en cada nivel se considera dos tipos de datos: hombres y mujeres.

En esta sección analizaremos el caso de una variable.

Modelo Completamente Aleatorizado o PRUEBA DE K - MEDIAS

Este modelo se caracteriza por que los datos que constituye la muestra son seleccionados para cada tratamiento de manera aleatoria.

Estructura del problema:

Supongamos que un equipo de médicos está interesado en probar si ciertos medicamentos pueden tener cierta efectividad al aplicárseles a un conjunto de pacientes. Para ello selecciona aleatoriamente a nj pacientes para aplicarles el j-ésimo medicamento.

Los datos se presentan en la siguiente tabla:



El modelo:

Sea X la variable que representa la medida de una determinada característica de la población en estudio.

Si en base a esto definimos a xij como la medida o valor del i-ésimo elemento obtenido en el j-ésimo tratamiento, podemos decir que el modelo de una variable completamente aleatorizado se puede expresar como

x_ij = μ+ β_j +e_ij,     i = 1, 2, …, n_j ; j = 1, 2, … k

Frente a este modelo podemos formular las siguientes hipótesis:

Ho: μ₁ = μ₂ = ⋯ = μ_k
H1: μ_i ≠ μ_j para algún i ≠ j

Nivel de significación de la prueba: α

Estadístico de la prueba:
Para esto debemos construir la Tabla del Análisis de la Varianza

Deducción de la tabla:

Como



Suma de los cuadrados de los desvíos por columna o tratamiento = SCTR, talque


Luego, tenemos: SCT = SCE + SCTR (ecuación 1)

Como estas sumatorias expresan parte de una varianza, podemos estimar la varianza poblacional en cada caso por el método de los estimadores máximo verosímiles, tomando en cuenta nuestra primera advertencia, podríamos decir que al dividir a cada uno de ellos por sus respectivos grados de libertad obtendremos los llamados cuadrados medios.

Esto es:
Cuadrado medio de los tratamientos: CMTR= SCTR/(k-1)

Cuadrado medio de los errores: CME= SCE/(n-k)

Del mismo modo y desde antes de esto, la varianza total; es decir los errores totales tienen por grados de libertad a (n-1) por lo que S² 0 = SCT/(n-1)
Como se obtuvo (n-k), simplemente de la ecuación (1): n-1 = x + (k-1)
Por lo que la tabla del Análisis de la Varianza para este modelo será:



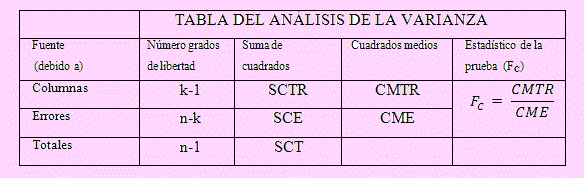
Criterio de decisión: Usado en Excel:

Si F_C  > F _α (k-1,n-k) rechazaremos Ho; es decir, podemos decir que no hay diferencia significativa entre el efecto medio de las poblaciones a las cuales se les aplicó el tratamiento. En caso contrario, existirá por lo menos un pareja de medias en los cuales hay diferencia significativa

El siguiente paso podría consistir ahora en tratar de determinar cuáles son esas parejas de medias. El procedimiento consiste en encontrar el intervalo de confianza del 100(1-α)% para cada par de medias. Allí tendremos la respuesta y más aún, encontrar cuál de ellas difiere más o menos que las otras.

ANOVA EN EXCEL

El programa Excel posee herramientas para resolver problemas de diseño de experimentos en el caso de tres modelos mencionados anteriormente.
Lo veremos para caso que contemplemos:

Ejemplo 01

El gerente de operaciones de una gran tienda de almacenes desea comparar las ventas realizadas por los 4 locales con los que cuenta la empresa. El gerente selecciona al azar las ventas realizadas durante 5 fines de semana para cada una de las sucursales. Los resultados de las ventas en miles de dólares se presentan a continuación:



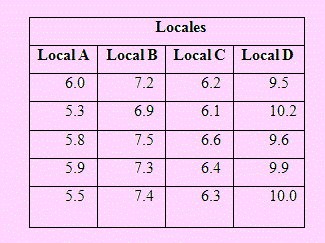
Asumiendo que las ventas se distribuyen normalmente
a) Pruebe si existen diferencias significativas entre las ventas promedio realizadas por las 4 sucursales. Use α = 0.05.
b) ¿Cuál de los cuatro locales presenta las mayores ventas?

Solución

Procedimiento:
Primero introduciremos los datos hacia la primera hoja de un nuevo libro, conforme se muestra en la tabla anterior.



A continuación usaremos la secuencia:
[Datos] – [Análisis de datos] – [Análisis de varianza de un factor]



Luego del cual obtendremos la siguiente ventana de diálogo:



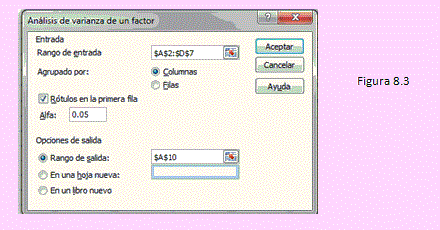
Luego de hacer clic en [Aceptar] obtendremos los siguientes resultados:

a) El estadístico de la prueba: FC = 257.674419
Según el problema: n = 20; k = 4

El valor crítico: F_α(k-1,n-k) = F_α( 3,16) = Distr.F.Inv(0.05,3,16) = 3.238871522

Criterio de decisión:

Como F_C > F_α entonces rechazaremos Ho; esto significa que sí hay diferencia significativa en el promedio de las ventas entre estas cuatro tiendas.



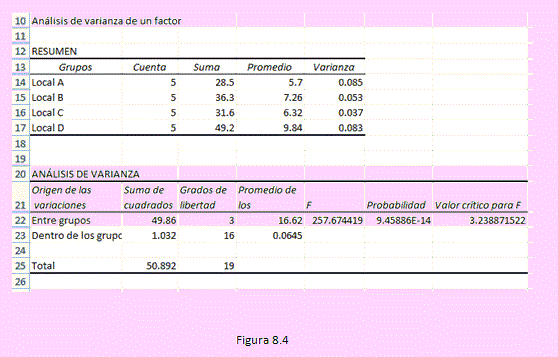
También podemos comparar elpValor (probabilidad) con α. Si pValor < α entonces se rechazará la hipótesis nula.

b) Dos formas de responder a esta pregunta: Se puede formular hipótesis de doble cola para todos los pares de medias usando t de Student; tema ya estudiado.

Se debe tomar pares de medias μ_i y μ_j ; para i ≠ j ,con i,j = 1, 2, .. , k que es el número de tratamientos o número de columnas y se obtiene el intervalo de confianza para μ_i - μ_j.

Por Bloques Completamente Aleatorizado

En este modelo, además de los tratamientos que es un tipo de variable los datos de las muestras de cada tratamiento se agrupan para formar el concepto de FACTOR, el cual a su vez puede ser sometida a un análisis de comparación de los efectos que se encuentren entre los bloques, por ello el modelo en este caso es:

x_ij = μ + α_i + β_j + e_ij,     i = 1, 2, …, n_j ; j = 1, 2, … k, i = 1, 2, …, l

Frente a este modelo podemos formular las siguientes hipótesis:

Hipótesis de igualdad de medias poblaciones de los tratamientos:
Ho: μ_.1 = μ_.2 = ⋯ = μ_.k = μ
H1: μ_.i ≠ μ_.j para algún i ≠ j

Hipótesis de igualdad de medias poblacionales por bloque:
Ho: μ_1. = μ_2. = ⋯ = μ_l. = μ
H1: μ_i. ≠ μ_j. para algún i ≠ j

La deducción de la tabla del ANOVA es similar al modelo anterior, lo cual, en este caso es:



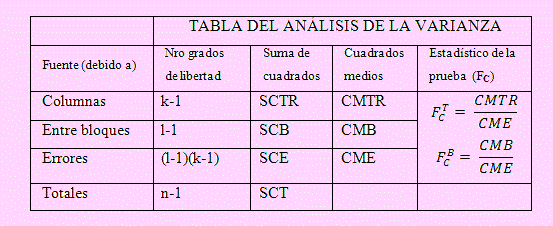
Criterio de decisión para tratamientos:
SiF_C >F_α (k-1,n(k-1)(l-1))se rechazará la hipótesis nula.

Criterio de decisión para los bloques:
SiF_C > F_α (l-1,(k-1)(l-1)) se rechazará la hipótesis nula.

Ejemplo 02

Una empresa fabricante de componentes para motores diesel debe reemplazar sus máquinas antiguas cuyo costo era bastante oneroso a fin de competir con sus competidores asiáticos. Por esta razón el gerente de producción ordenó someter a estudio cuatro nuevos tipos de máquinas y se probaron por un tiempo encontrándose la producción del número de componentes por hora de cada una de ellas; los datos se muestran en la siguiente tabla:



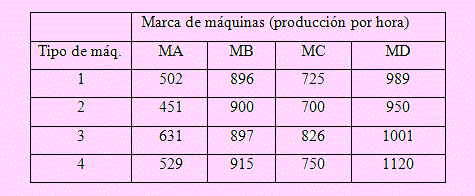
Para tomar una decisión adecuada se planea formular las siguientes hipótesis:

a) No hay diferencia significativa en la producción medias entre las máquinas
Ho: μ_A = μ_B = μ_C = μ_D
H1: μ_i ≠ μ_j para algún i ≠ j

b) No hay diferencia significativa en la producción promedio por tipo de máquina

Ho: μ₁ =μ₂ = μ₃ = μ₄
H1: μ_i ≠ μ_j para algún i ≠ j Ingresando los datos a otra hoja vacía tendremos



y usando la opción que se indica: Análisis de dos factores con una sola muestra, se tendrá la siguiente ventana de diálogo:



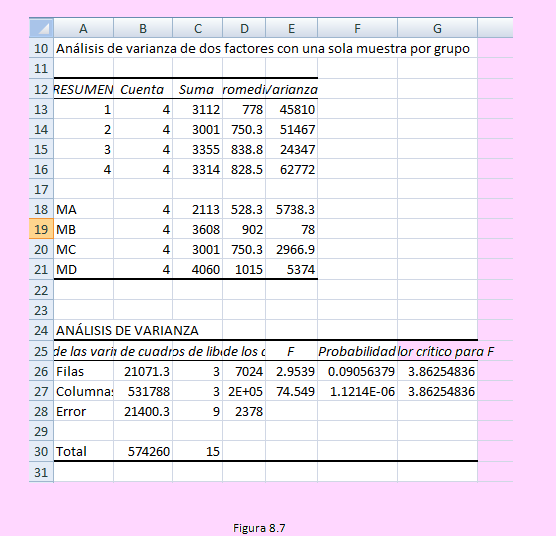
Con lo cual obtendremos la siguiente salida de resultados:



Criterio de decisión:

En el caso de la hipótesis por máquina: Rechazaremos Ho pues el Fc es mayor que el f crítico (74.59 > 3.86254836)

Pero en el caso de la hipótesis por tipo de máquina no se rechaza Ho pues el Fc = 2.9539 no es mayor a el F crítico = 3.86254836

Es decir, la producción promedio de componentes por hora es significativa entre los tipos de máquinas.

Por otro lado, entre las máquinas no hay diferencia significativa en la producción promedio.

Si se decide usando el pValor diríamos: En el caso de las máquinas: Como pValor = 0 < α = 0.05 entonces rechazaremos Ho.

Del mismo modo, en el caso de los bloques: Como pValor = 0.0906 no es menor que α = 0.05 entonces no se rechaza Ho.

Pregunta:

Por qué la respuesta anterior (en cursiva) se expresa como dos respuestas independientes? Se responde si hay diferencia en promedios de producción por máquina y se responde si hay diferencia o no en promedios de producción por tipo de máquina. Y porqué no responde por una ocurrencia simultánea; es decir, que hay una interacción, que hay un evento que ocurre como una interacción entre tratamientos y bloques? Que la variabilidad de los errores se debe a la influencia de las máquinas y los tipos de máquinas?

Esto es lo que pretende el siguiente modelo en el cual tanto a tratamiento como a bloques se les define como dos variables independientes y se trata de encontrar explicación en la interacción entre ellas, además de la influencia entre los tratamientos, entre los bloques y dentro de los tratamientos.

8.3 MODELO DE CLASIFICACIÓN DE DOS VARIABLES

Lo dicho en la pregunta anterior nos releva de otros comentarios. A cada variable se la considera como un Factor, uno independiente de otro. A su vez este modelo se divide en dos:

Cuando por cada bloque y por cada tratamiento (una celda) se presenta un solo elemento constituyendo una muestra de tamaño uno.

Y cuando en cada bloque y cada tratamiento se presentan un conjunto de elementos por lo que la muestra tiene un tamaño mayor a uno y en el cual se detecta alguna forma de interacción.

El primero constituye modelo si repetición o sin replicación y el segundo modelo con repetición o con replicación.

Sin Replicación Ahora presentaremos el modelo para formular las hipótesis y pasar a presentar la tabla del análisis de la varianza correspondiente.

Como antes, se X la característica de una población bajo estudio. Un valor de esta variable puede ser expresada como xij que representa el efecto obtenido por la combinación del i-ésimo bloque y el j-ésimo tratamiento.

Por lo que x_ij = μ + α_i + β_j + γ_ij + e_ij, i = 1, 2,…, n_j; j = 1, 2,… k, i = 1, 2,…, l

Si se compara con el modelo anterior, se verá que sólo se ha añadido el componente de la interacción de filas y columnas: γ_ij

Este es un ejemplo esquemático del modelo:

Para optar a una maestría en una universidad extranjera se debe pasar por un período de entrenamiento y capacitación para luego presentarse el examen. Los programas de preparación son de tres tipos: Una sesión de repaso de 3 horas, un programa de un día y un curso de 10 semanas. Por otro lado, por lo general a este examen se presentan licenciados en Administración, Ingeniería y de Artes y Ciencia.

Según esto, un factor a ser estudiado es si la licenciatura de un postulante puede afectar a su calificación en la prueba. Un segundo factor a ser estudiado es si la forma de preparación que elija el postulante puede afectar su calificación en la prueba.

Cualquiera de los dos factores constituirán los tratamientos y el otro, los bloques.

La tabla del ANOVA será la misma excepto que el componente que antes generaba una variabilidad por bloques es generado por una nueva variable o un segundo factor, siendo los tratamientos el primero.

Las hipótesis y la tabla es la misma, de manera que pasaremos a resolver un ejemplo al respecto

Ejemplo 03

Una empresa de investigaciones prueba el rendimiento, en millas por galón, de tres marcas de gasolina. Como la gasolina tiene un rendimiento diferente en las diferentes marcas de automóviles, se seleccionaron 5 marcas de automóviles las que se consideraron como bloques en el experimento; es decir, cada marca se prueba con cada tipo de gasolina. Los resultados del experimento, en millas por galón, son los siguientes:



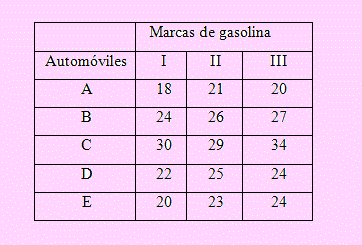
Formulación de la hipótesis:

Respecto a las marcas de gasolina:
Ho: El rendimiento medio en los tres tipos de gasolina es la misma
H1: Hay diferencia significativa en el rendimiento entre el tipo de gasolina

Respecto a la marca de automóvil:

Ho: La marca de automóvil no afecta en el rendimiento medio
H1: El rendimiento medio entre las marcas de automóvil es diferente.
Ingresando al Excel como el ejemplo anterior, tendremos los siguientes resultados:



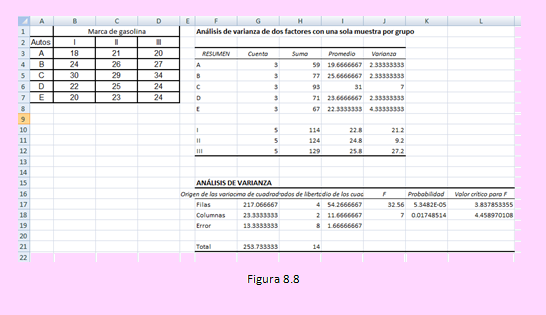
Criterio de decisión:

Como en ambos factores el estadístico Fc es mayor al valor crítico F a un nivel de significación del 5%, podemos afirmar que:

El rendimiento medio difiere entre las marcas de gasolina.
El rendimiento medio es diferente entre las marcas de automóviles.

Con Replicación

En este último caso, se consideran dos factores y por cada valor del factor por fila y por columna se disponen de muestras de tamaño mayor que uno. De allí que el modelo pretende explicar la variabilidad de los datos debido a la interacción entre los dos factores. El modelo es el siguiente:

x_ij = μ + α_i +β_j + γ_ij + e_ijh, i = 1, 2,…, n_j ; j = 1, 2,… k, i = 1, 2,…, l

En este modelo e_ijh representa la interacción entre los dos factores i y j y además el efecto con el aporta el h-ésimo elemento de la muestra. El siguiente esquema nos muestra el estado de una celda cualquiera.

 

	Factor j
Factor i	n1   n2   ...   nh

Formulación de las hipótesis:

a) Debido a los tratamientos (Factor 1):

Ho: No hay diferencia en el efecto medio entre los tratamientos
H1: Hay alguna diferencia entre los efectos medios de algunos de ellos

b) Debido a los bloques o filas (Factor 2):

Ho: El efecto medio entre los bloques o factor 2 es la misma
H1: El efecto medio difiere entre los bloques

c) Debido a las interacciones entre el factor 1 y el factor 2:

Ho: No existe interacción en el efecto medio de tratamientos y bloques.
H1: Sí existe diferencia significativa entre ellos.

Tabla del ANOVA:



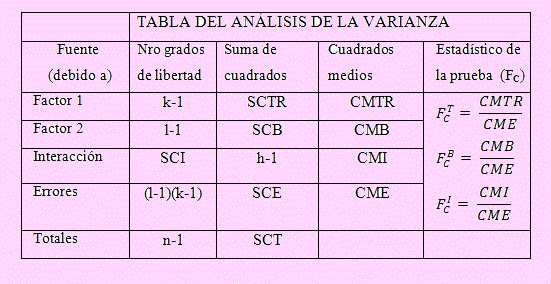
Lo nuevo en esta tabla: SCI = Suma de cuadrados de las interacciones
Grados de libertad de la varianza de las interacciones: h-1
CMI= SCI/(h-1)

Ejemplo 04

Tomando en cuenta el problema del acceso a la maestría por postulantes egresados con diferentes licenciaturas, tenemos los datos en el siguiente cuadro. Formule las hipótesis correspondientes y a partir de la tabla del ANOVA compruebe las hipótesis formuladas.



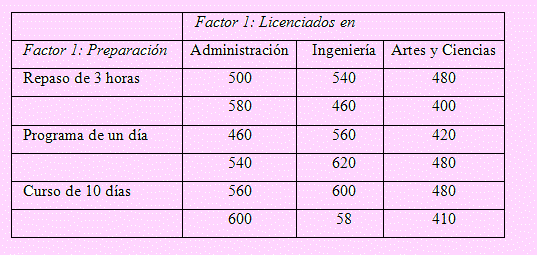
Los datos se ingresaron al Excel como se muestra en la siguiente imagen:



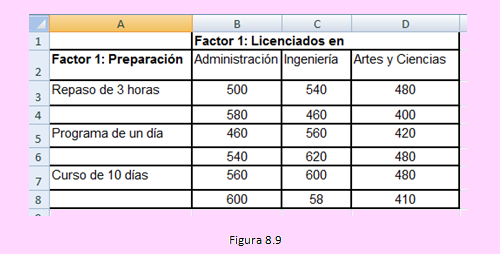
A continuación, usando la opción y llenando la ventana siguiente como se muestra,





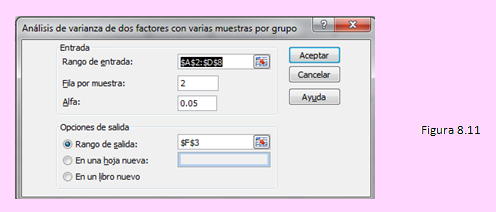
Se obtuvieron los siguientes resultados:



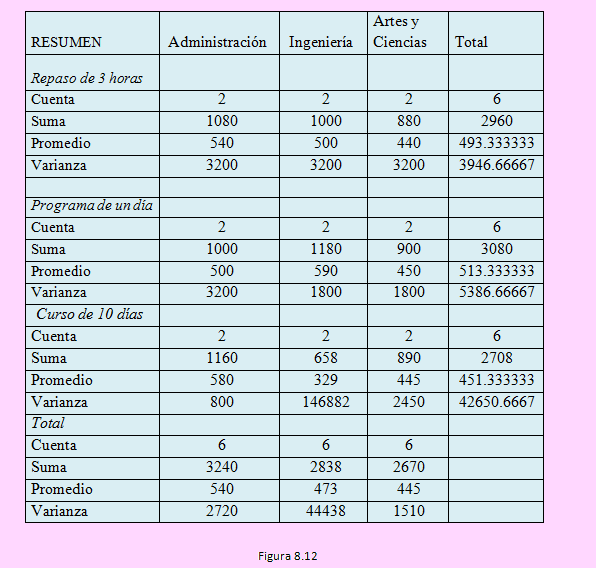
Y la tabla ANOVA es la siguiente:



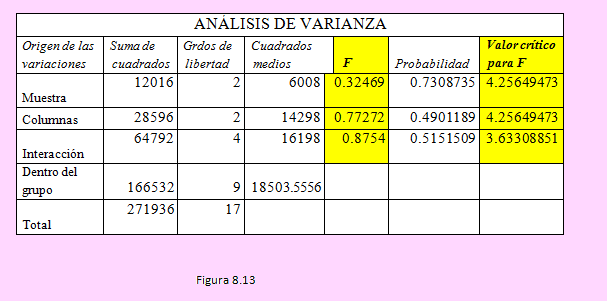
Observando la tabla podemos comprobar que, como los estadísticos de la prueba (F_C) para cada pareja de hipótesis planteada es menor que el valor crítico correspondiente, no se rechaza la hipótesis nula, en consecuencia podemos afirmar:

a) El factor preparación para el examen de postulación no tiene efecto significativo sobre los postulantes.
b) El tipo de licenciatura de cada postulante no afecta significativamente en el acceso a la maestría
c) No hay interacción entre la forma cómo se preparen para la prueba ni el tipo de especialidad que tengan.

8.4 PROBLEMAS PROPUESTOS

1. Se han propuesto tres métodos distintos para ensamblar un nuevo producto. Se eligió un diseño experimental totalmente aleatorizado para determinar cuál de los métodos da como resultado la mayor cantidad de partes producidas por hora, y se seleccionaron al azar a 30 trabajadores, asignándoles uno de los métodos propuestos. La cantidad de unidades que produjo cada trabajador fue la siguiente:



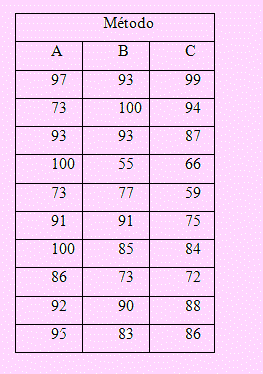
Utilice estos datos y comprueba si la media del número de partes producidas es la misma en cada método. Use un nivel de significación del 5%.

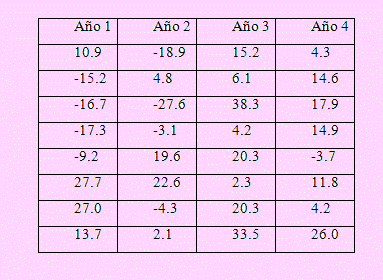
2. A continuación vemos los cambios porcentuales en el Promedio Industrial del Dow Jones en cada uno de los cuatro años de los seis períodos presidenciales. ¿Parece haber algún efecto importante debido al año del período presidencial sobre el desempeño del mercado accionario? Use α = 0.05.



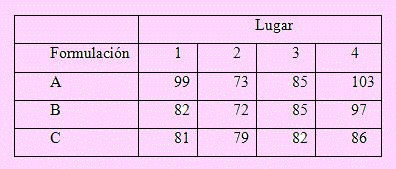
3. Se probaron tres formulaciones distintas para reparación de asfalto en cuatro lugares de una carretera. En cada lugar se repararon tres secciones de la carretera; cada sección con uno de los tres compuestos. A continuación se obtuvieron datos acerca de la cantidad de días de uso hasta que se requirió nueva reparación. Estos datos se ven en la siguiente tabla. Con α = 0.01, prueba si hay alguna diferencia importante en las formulaciones.



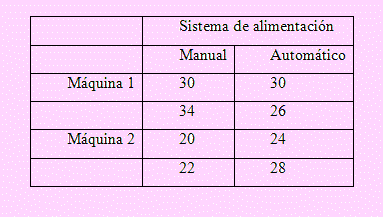
4. Una empresa manufacturera diseñó un experimento factorial para determinar si la cantidad de partes defectuosos producidas por dos máquinas es distinta, y si esa cantidad también depende de si la materia prima para cada máquina se alimentaba en forma manual o con un sistema automático. Los datos de la tabla muestran las cantidades producidas de partes defectuosas. Use α = 0.05 y vea si hay algún efecto importante debido a las máquinas al sistema de carga y a su interacción.



Siguiente sesión.