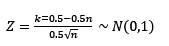
Razones por las que se usan estas pruebas
1. Son más rápidos y fáciles de aplicar (cálculos aritméticos simples).
2. Con frecuencia son más fáciles de entender.
3. Son relativamente insensibles a datos atípicos.
4. El tipo de supuestos requeridos son en general más fáciles de cumplir.
5. Se pueden aplicar en muestras pequeñas donde no se pueden verificar los supuestos de la estadística inferencial clásica.
6. Resuelven preguntas en nuevos escenarios, por ejemplo, cuando se trabaja con variables medidas en escalas nominales.
Prueba del signo
Se supone que la variable es continua, aunque puede aplicarse a una ordinal usando la mediana
La hipótesis nula: Ho: Me = Mo.
Ejemplo 1
Los siguientes datos corresponden a los pesos de 12 niñas de 5 años de edad. ¿Qué se puede afirmar respecto al peso mediano si se supone que es igual a 19?
15.0 17.3 18.3 21.9 13.8 20.8 17.5 19.7 15.1 26.7 20.4 16.4
Cuando el tamaño de la muestra es mayor a 12, se usa el estadístico:
Debemos instalar el paquete: BSDA. Luego del cual, lo cargamos a memoria
>library(BSDA)
Ingresamos los datos:
> p=c(15.0, 17.3, 18.3, 21.9, 13.8, 20.8, 17.5, 19.7, 15.1, 26.7, 20.4, 16.4)
Prueba de dos colas:
> SIGN.test(p, md = 19, alternative ="two.sided", conf.level = 0.95)
Observando el pValue Podemos afirmar que no existe suficiente razón para rechazar Ho.
Las otras pruebas:
> SIGN.test(p, md = 19, alternative ="greater", conf.level = 0.95)
> SIGN.test(p, md = 19, alternative ="less", conf.level = 0.95)
En todos ellos no se rechaza Ho.
Una prueba de datos pareados:
Se piensa que la susceptibilidad a la hipnosis disminuye con cierto entrenamiento. Se aplicó a 6 individuos una escala para medir la susceptibilidad antes y después del entrenamiento encontrando los siguientes resultados:
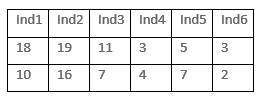
>antes=c(18,19,11,3,5,3)
>despues=c(10,16,7,4,7,2)
Ho: La susceptibilidad se mantiene (no se logra reducir; ambas medianas son iguales)
Probemos las tres hipótesis
> SIGN.test(antes, despues, alternative="t", conf.level=0.95)
> SIGN.test(antes, despues, alternative="g",conf.level=0.95)
>SIGN.test(antes, despues, alternative="l",conf.level=0.95)
No se logra reducir.
Prueba de rangos de signos de Wilcoxon
La variable a ser usada es continua y puede ser aplicada a variables de escala de intervalos.
La muestra proviene de una población con distribución simétrica, lo que significa que la media y mediana son iguales, en cuyo caso Ho puede referirse a la media o mediana. Como en el caso anterior, esta prueba se puede aplicar para datos pareados.
Ejemplo 2
Algunos clientes se han quejado sobre los tiempos de duración de las pilas producidas por una empresa. Se tomó una muestra y se midió su duración. ¿Se puede concluir que la mediana de la duración de las pilas es diferente a 18?
Carguemos los datos:
>pila=c(18.4,19.0,17.0,17.0, 18.6, 17.2, 19.2, 17.1, 18.5, 16.0, 16.1, 18.4, 16.9, 19.4, 16.8, 18.2, 18.4, 18.3, 18.1, 17.1)
Ho: Me = 18
En esta prueba se dispone de dos métodos: wilcox.test de la librería MASS y wilcox.exact de la librería exactRankTests. El último se usa cuando los datos presentan empates.
Instalemos las dos librerías y luego los cargamos a memoria.
>library(MASS)
>library(exactRankTests)
> wilcox.test(pila,mu=18,exact=F, alternative="t",conf.int=0.95)
Probemos ahora con wilcox.exact:
> wilcox.exact(pila,mu=18,exact=T, alternative="t",conf.int=0.95)
Datos pareados
Se contaron la cantidad de paquetes de artefactos embalados por 6 trabajadores de dos turnos y se encontraron los siguientes resultados:
Al 5% de significación, se puede afirmar que no existe diferencia significativa en el rendimiento mediano de los trabajadores de ambos turnos?
Ho: MedM = MedT
Cargamos los datos
>tm=c(201,182,191,188,188,174)
>tt = c(203,178,186,183,181,165)
> wilcox.test(tm,tt,paired=T,exact=F,correct=F,conf.int=0.95)
Prueba U de Mann Whitney – Wilcoxon
En esta prueba, los datos son de naturales continua, aunque, también puede resolverse con datos ordinales. Se trata de probar la hipótesis de independencia de dos muestras. Similar a la prueba de igualdad de medias de la distribución t de Student usado en la estadística paramétrica.
Ho: Las dos muestras son independientes.
Ejemplo 3
A continuación, se presenta el tiempo de atención (en minutos) para dos diferentes ventanillas de atención al cliente. Se anotó el tiempo necesario para atender a 10 clientes de cada ventanilla escogidos al azar y de manera independiente, los clientes seleccionados realizaron operaciones similares. Los resultados se muestran en la siguiente tabla:
¿Con 5% de significación se puede afirmar que el tiempo de atención mediano es diferente en las dos ventanillas?
Definimos las variables:
>v1=c(13,10,12,9,10,18,13,8,11,9)
>v2=c(20,15,21,20,23,13,17,14,30,10)
Cargamos la librería exactRankTests.
>library(exactRankTests)
Usaremos la función wilcox.exact().
> wilcox.exact(v1,v2, exact=T, alternative = "t", conf.int=0.95)
Se rechaza Ho, en consecuencia, el tiempo de atención en las dos ventanillas difieren significativamente.
Si el parámetro alternative es F, se usa el estadístico U, sin ajustar por normal.
Ejemplo 4
Los datos
Ho: Mediana(dia 1) = Mediana(dia 2)
>d1=c(1.6, 0.5, 1.2, 1.3, 0.3, 0.7, 1.1, 1.2, 1.8, 0.8)
>d2=c(0.2, 0.1, 0.7, 0.5, 0.4, 0.6, 0.4, 0.3, 0.4, 0.7)
> wilcox.exact(d1,d2, exact=T, alternative = "t", conf.int=0.95)
Con un pVlue = 0.00255, al 5% de nivel de confianza, podemos afirmar que la cantidad mediana de jalea en los dos días difieren significativamente.
Prueba de Kruskall – Wallis
Usado para probar que dos o más muestras son independientes, lo cual se hace probando la igualdad de sus medianas o medias. Es la prueba alternativa para los casos en que no se puede usar el diseño de experimentos en el modelo completamente aleatorizado de k muestras cuando no cumplen las pruebas de normalidad y homosedasticidad. En este caso las variables son continuas y también pueden estar medidos en escala ordinal.
El gerente de la empresa R&D S.A. dedicada a la compra y venta de inmuebles desea comparar el acabado final (medido en una escala de 1 al 20) de edificaciones realizadas por tres empresas constructoras. Los resultados de evaluar algunas edificaciones elegidas al azar de manera independiente de estas tres empresas constructoras se presentan a continuación:
Verifique si el acabado final de las edificaciones es diferente realizada por al menos una de las empresas constructoras.
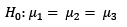
>library(stats)
Definimos los vectores:
>gs=c(15,14,12,8,13,10)
>bf=c(12,13,11,12,14)
>rd=c(16,18,14,16,15,13)
La prueba
>kruskal.test(list(gs, bf, rd))
Los resultados indican que se debe rechazar la hipótesis nula, en consecuencia, podemos decir que no existe suficiente evidencia para afirmar que el acabado final sea la misma en todas las empresas.
Ejemplo 6
Se aplicó una escala para medir el estado de salud (VES) auto-reportado por personas de distintos grupos étnicos. La escala toma valores entre 0 y 100 donde a valores altos indican mejor estado de salud. Los resultados se presentan a continuación:
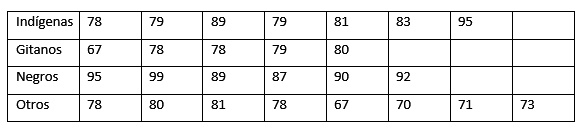
>ind=c(78, 79, 89, 79, 81, 83, 95)
>git=c(67, 78, 78, 79, 80)
>neg=c(95, 99, 89, 87, 90, 92)
>otr=c(78, 80, 81, 78, 67, 70, 71, 73)
La prueba
>kruskal.test(list(ind, git, neg, otr)
Podemos afirmar que el estado de salud entre un grupo y otro difiere significativamente.
Prueba de Friedman
En esta prueba los datos constituyen una variable continua, en un conjunto de k muestras que constituyen k tratamientos en un modelo de diseño de experimentos en el caso de bloques aleatorizados en que no se cumple con las pruebas de normalidad y sedasticidad.
La hipótesis nula es Ho: Las k muestras tienen la misma distribución
Ejemplo 7
Una muestra de 10 alumnos elegidos al azar participa en la evaluación de la actividad docente en cierta Universidad, opinando acerca de tres profesores a cuyas clases asisten. Si las puntuaciones otorgadas (de 1 a 5) sobre la utilidad de los materiales que utilizan son las siguientes:
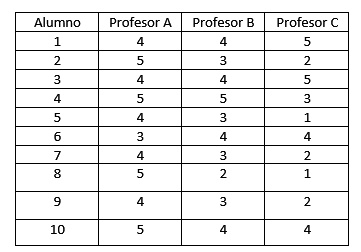
¿Podemos afirmar con 2% de significación que las valoraciones de los profesores difieren?
Nota:
Todos los datos que provienen del cruce de dos o más variables categóricas, deben tener el siguiente formato de tabla, antes de ser ingresados al programa:
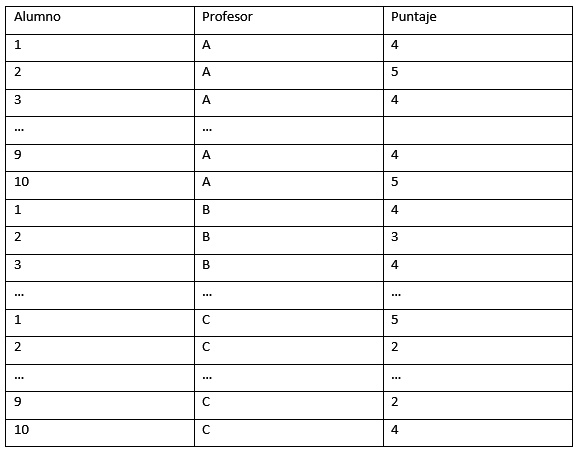
Definamos una matriz a partir de estos datos:
>alum=matrix(c(4,5,4,5,4,3,4,5,4,5,4,3,4,5,3,4,3,2,3,4,5,2,5,3,1,4,2,1,2,4),nrow=10, ncol=3,dimnames=list(1:10,c("Profesor A","Profesor B","Profesor C")))
> alum
Usemos la prueba
> friedman.test(alum)
Según el pvalue podemos afirmar que al 2% de significación, las calificaciones a los profesores difieren significativamente
Ejemplo 8
Se usan 4 tipos de fertilizantes en 6 tipos diferente de terreno. Se toma una muestra de la producción de una temporada y estos son los resultados:
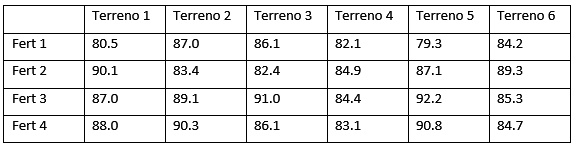
a) ¿Se puede afirmar que existe suficiente evidencia que el volumen de la producción difiere en al menos un tipo de fertilizante?
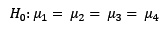
b) ¿Es cierto que el volumen de producción depende del terreno donde se cultiva?
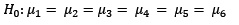
Como en el ejemplo anterior, para este modelo, tres columnas: pr, que contendrá los datos ordenados por columna; tr, que contendrá los nombres de columna, repetido cada uno de ellos, 4 veces y b que contendrá las categorías de los fertilizantes, de 4 en 4, por cada columna de tratamiento.
>pr = c(80.5, 90.1, 87.0, 88.0, 87.0, 83.4, 89.1, 90.3, 86.1, 82.4, 91.0, 86.1, 82.1, 84.9, 84.4, 83.1, 79.3, 87.1, 92.2, 90.8, 84.2, 89.3, 85.3, 84.7)
> tr=c("Terr 1","Terr 1","Terr 1","Terr 1","Terr 2", "Terr 2", "Terr 2", "Terr 2", "Terr 3", "Terr 3", "Terr 3", "Terr 3", "Terr 4", "Terr 4", "Terr 4", "Terr 4", "Terr 5", "Terr 5", "Terr 5", "Terr 5", "Terr 6", "Terr 6", "Terr 6", "Terr 6")
> b=c("Fert 1","Fert 2","Fert 3","Fert 4", "Fert 1","Fert 2","Fert 3","Fert 4", "Fert 1","Fert 2","Fert 3","Fert 4", "Fert 1","Fert 2","Fert 3","Fert 4", "Fert 1","Fert 2","Fert 3","Fert 4", "Fert 1","Fert 2","Fert 3","Fert 4")
a) Para probar esta hipótesis debemos ingresar el siguiente comando:
> friedman.test(pr,b, tr) # otra forma: > friedman.test(pr~tr |
Según el pValue, la producción promedio difiere significativamente por el tipo de fertilizante.
b) El siguiente comando probará este supuesto:
> friedman.test(pr,tr,b) # otra forma: > friedman.test(pr~b | tr)
La producción promedio difiere significativamente según el terreno de cultivo.
Coeficiente de correlación de rangos de Spearman
Esta prueba trata de probar la hipótesis de independencia de variables bajo el concepto de la correlación.
Ejemplo 9
Se trata de evaluar la relación entre inequidad de la mortalidad evitable (IME) y un indicador que mide las necesidades básicas insatisfechas (NBI) en un grupo de ciudades. Para ello se tomó una muestra de 25 ciudades y se obtuvieron los siguientes datos:
IME: 0.893, 0.904, 0.884, 0.912, 0.897, 0.904, 0.937, 0.918, 0.906, 0.945, 0.916, 0.916, 0.870, 0.911, 0.914, 0.887, 0.907, 0.890, 0.877, 0.854, 0.859, 0.866, 0.882
NBI: 18.2, 17.5, 7.7, 32.7, 26.7, 16.0, 26.9, 24.9, 34.0, 71.3, 43.0, 20.1, 22.2, 32.9, 36.9, 22.8, 27.4, 17.0, 17.8, 12.7, 37.6, 22.5, 12.7
Ahora la prueba
>cor.test(IME,NBI,method ="spearman", exact = TRUE)
Si cambiamos el parámetro exact, tenemos
>cor.test(IME,NBI,method ="spearman", exact = FALSE)
De una u otra forma, podemos afirmar que existe relación entre ambas variables.
Pruebas de bondad de ajuste
Es un método de prueba para verificar si un conjunto de datos tiene un determinado comportamiento; es decir, si pueden seguir un tipo de distribución conocida.
Ajuste a una normal
Ejemplo 1
El peso que deben contener ciertas bolsas de detergente es de 750 g con una tolerancia de 2 g. Se desea verificar si es razonable suponer que la distribución de peso es normal. Para ello se tomó una muestra de 25 bolsas, se pesaron y se obtuvieron los siguientes datos:
750.0, 749.3, 752.5, 748.9, 749.9, 748.6, 750.2, 748.4, 747.8, 749.3, 749.6, 749.0, 747.7, 748.3, 750.5, 750.6, 750.0, 750.4, 752.0, 750.2, 751.4, 750.9, 752.4, 751.7, 750.6
Antes de usar el método, podemos realizar un análisis de exploración de datos (EDA).
Pondremos los gráficos en una sola ventana dividido en tres columnas
>par(mfrow=c(1,3))
<
Definimos una variable
>x=c(750.0, 749.3, 752.5, 748.9, 749.9, 748.6, 750.2, 748.4, 747.8, 749.3, 749.6, 749.0, 747.7, 748.3, 750.5, 750.6, 750.0, 750.4, 752.0, 750.2, 751.4, 750.9, 752.4, 751.7, 750.6)
Tracemos un histograma
< hist(x,xlab="Peso",ylab="Frecuencia",las = 1, main = "Peso de bolsa de detergente")
Gráfico de la función de densidad
> plot(density(x), xlab="Peso",ylab="Densidad", las=2, main="Peso de una bolsa de detergente")
> qqnorm(x,xlab="Cuantiles teóricos",ylab="Cuantiles muestrales",las=1,main="Prueba de normalidad")
La gráfica en la prueba
> qqline(x)
Puesto que la distribución a la cual se desea ajustar los datos, tiene dos parámetros, debemos estimarla mediante las estadísticas muestrales (la media y varianza). Esto lo hacemos con la función fitdistr() que pertenece al paquete MASS, que debemos cargarlo a memoria
>library(MASS)
Ahora ya podemos usar la función que permite estimar los parámetros
>pestim=fitdistr(x,"normal")
< >pestim
Esto nos muestra las estimaciones y el desvío de las mismas
Ahora usaremos la prueba de Kolmogorov – Smirnof, usando la prueba ks.test() que usa como argumento a los dos parámetros estimados (media y dsviación estándar).
>ks.test(x, "pnorm", mean = pestim$estimate[1], sd = pestim$estimate[2])
Según el pValue, no se rechaza la hipótesis nula; en consecuencia, los datos pueden ajustarse a una distribución normal.
Prueba de Anderson Darling
Para ello usaremos la función ad.test del paquete goftest.
>library(goftest)
Usamos la prueba, en la cual se requiere los mismos argumentos que ks.test.
> ad.test(x, "pnorm", mean=pestim$estimate[1], sd = pestim$estimate[2])
Esto confirma la conclusión anterior.
Probemos gráficamente
Restableceremos el entorno de la ventana de gráfico:
>par(mfrow=c(1,1))
Vamos a generar un conjunto de puntos a partir de x:
>y = seq(min(x), max(x), by = 0.0001)
> plot(y, dnorm(y, mean = pestim$estimate[1], sd = pestim$estimate[2]), type = "l", col = "red", xlab="x", ylab = "pnorm(x, mean, sd)")
Su distribución acumulada
> plot(y, pnorm(y, mean = pestim$estimate[1], sd = pestim$estimate[2]), type = "l", col = "red", xlab="x", ylab = "pnorm(x, mean, sd)")
Ahora graficamos la distribución acumulada
>plot(ecdf(x), add = TRUE)
Ajuste a una distribución proporcional
Ejemplo 2
La empresa de investigación de mercado D&J S.A. hizo un estudio para determinar la opinión de los televidentes sobre un nuevo programa humorístico. Se tomó una muestra aleatoria de 400 personas, obteniéndose los siguientes resultados:
Pruebe si la opinión de los televidentes respecto al nuevo programa humorístico no se distribuye en la proporción: 2:4:6:5:3. Use = 0.01.
Los valores proporcionales: 2/20 = 0.1, 4/20 = 0.2, 6/20 = 0.3, 5/20 = 0.25, 3/20 = 0.15.
Definamos las variables: ft (frecuencias teóricas) y p (las proporciones o probabilidades)
>ft = c(25, 60, 175, 120, 20)
>p = c(0.1, 0.2, 0.3, 0.25, 0.15)
Usamos la prueba chisq.test()
Debemos construir una matriz de cinco filas con dos columnas para usar la prueba chisq.test()
>m=matrix(c(ft,p),nrow=5, ncol=2)
Ahora usamos la prueba
>chisq.test(m)
A un nivel de significación del 5% diríamos que sí se ajustan a dicha distribución proporcional
Nota:
Se pudo haber definido también una dataframe con las dos variables.
Ajuste a una distribución de Poisson
Ejemplo 3
El gerente de operaciones de Bancaper, entidad financiera que opera a nivel nacional, quiere estudiar si el número de solicitudes de crédito recibidas por día, se ajusta la distribución de Poisson. Se seleccionaron 300 días de operaciones, con lo cual el gerente elaboró el siguiente cuadro:
¿Sería razonable concluir que la distribución del número de solicitudes diarias de préstamo no es del tipo Poisson? Use el nivel de significación del 5%.
Definamos ft (frecuencias teóricas)
>ft = c(50, 77, 81, 48, 31)
Observe que no se incluye el último valor pues “5 o más”. Este valor lo insertaremos después, cuando sepamos la probabilidad que le corresponde. Haremos lo mismo con x.
>x = c(0, 1, 2, 3, 4)
Debemos obtener la función de probabilidad para hallar P(X≤4) y con esto hallamos P(X > 4).
Para ello antes debemos estimar el parámetro lambda:
>lambda=sum(x*ft)/sum(ft)
Ahora obtenemos la distribución de Poisson para los 5 valores de x
> p =dpois(0:4,lambda)
Como P(X <= 4) = sum(p), entonces P(X>4) = 1 – sum(p)
Luego, completaremos el valor que falta
>ft=c(ft,13)
< >p = c(p,1-sum(p))
Con tf y p definiremos la matriz, m de 6 filas y 2 columnas
Definamos un dataframe con ft y p:
>m = data.frame(ft,p)
Se puede definir también una matriz:
> m=matrix(c(ft,p),nrow=6,ncol=2)
Ahora ejecutamos la prueba:
>chisq.test(m)
Lo que indica que es cierto que los datos se ajustan a una distribución de Poisson.
Ajuste a una distribución exponencial
Ejemplo 4
Se desea determinar y construir una función de distribución del número de horas transcurridas hasta que falle un determinado componente de un celular. Para ello se toma una muestra de 20 celulares y se les deja conectados al suministro de energía, en un ambiente de 40ºC. Los datos obtenidos se muestran a continuación:
3.70 3.75 12.18 28.55 29.37 31.61 36.78 51.14 108.71 125.21 125.35 131,76 158.61 172.96 177.12 185.37 212.98 280.40 351.28 441.79
Definimos el vector x
>x = c(3.70,3.75,12.18,28.55,29.37,31.61,36.78,51.14,108.71,125.21,125.35,131.76,158.61,
172.96,177.12,185.37,212.98,280.40,351.28,441.79)
Puesto que la idea es no saber a qué tipo de distribución se la podría ajustar, trazaremos un histograma de frecuencias y la plotearemos
> hist(x, xlab="Tiempo", ylab="Frecuencia")
La forma de la curva nos sugiere que podemos ajustarla a una distribución exponencial.
Para comprobar, ploteemos 100 valores exponenciales:
generamos un conjunto de datos usando
> y=seq(0,3,by=0.02)
Ahora, para cada uno de ellos, generamos un valor exponencial en f
> f=dexp(y)
Ahora lo ploteamos
>plot(y, f)
Luego nuestra deducción es correcta.
Volviendo al problema, tenemos los datos en x, debemos estimar el parámetro alfa de la distribución X ---> E(α), sabiendo que el estimador es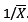 
Pero como podemos usar la función fitdistr para obtener este estimador más rápidamente. Como el paquete que lo contiene es MASS, debemos tenerlo cargado
>library(MASS)
>est =fitdistr(x, “exponential”)
>est
El promedio concuerda con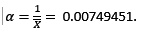 
Ahora vamos a probar si se ajusta
>ks.test(x,"pexp",rate=est$estimate[1])
Podemos apreciar que no se rechaza la hipótesis nula.
Si usáramos Anderson Darling para el cual instalamos y cargamos a memoria el paquete “goftest”
>library(goftest)
> ad.test(x,"pexp",rate=est$estimate[1])
Obtendríamos el mismo resultado.
Prueba de independencia de variables
Este tipo de prueba si dos variables categóricas son independientes o no. Los tipos de datos son nominales u ordinales.
Ho: Las dos variables son independientes.
Ejemplo 5
Una de las preguntas del estudio de una muestra de suscriptores de Bussiness Week fue: “Durante los últimos 12 meses, en viajes de negocios, ¿qué tipo de boleto de avión compró con más frecuencia?”. Las respuestas obtenidas se muestran en la siguiente tabla:
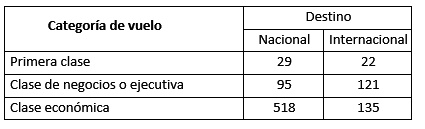
Usando nivel de significación 0.05, pruebe si existe relación entre el tipo de vuelo y el tipo de boleto.
Según el problema: Ho: Categoría de vuelo es independiente de tipo de boleto.
Como en el ejemplo 7 de alumnos que califican a sus profesores, definiremos una matriz para generar una tabla de contingencia:
>m=matrix(c(29,95,518,22,121,135), nrow = 3, ncol = 2, dimnames=list(c("Pc","Ej","Ec"), c("N","I")))
Ahora la prueba:
>chisq.test(m, correct=FALSE)
Ejemplo 6
Este es un ejemplo que se muestra en
http://vivaelsoftwarelibre.com/test-de-independencia-chi-cuadrado-en-r/
En 1976 se presentó un trabajo a cargo de Nanny Wermuth sobre 6851 nacimientos. Se tomaron dos factores, cada uno con cuatro variables:
Factor 1: Características de la madre
- jnf: Madre joven que no fumó durante el embarazo
- jf : Madre joven que fumó durante el embarazo
- mnf: Madre mayor que no fumó durante el embarazo
- mf : Madre mayor que fumó durante el embarazo
Factor 2: Estado del bebé
- pm: Prematuro que murió antes del primer año
- pv: Prematuro que vivió al menos el primer año
- gcm: Gestación completa que murió antes del primer año
- gcv: Gestación completa que vivió al menos el primer año
La tabla de nacimientos contados en cada categoría se muestra a continuación
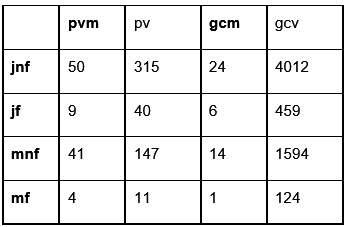
¿Están relacionadas las características de la madre con el estado del bebé?
Como en el ejemplo anterior, definimos la matrix mb, de la siguiente manera:
> mb=matrix(c(50, 9, 41, 4, 315, 40, 147, 11, 24, 6, 14, 1, 4012, 459, 1594, 124), nrow=4, ncol=4, dimnames=list(c("jnf","jf","mnf","mf"),c("pvm","pv","gcm","gcv")))
>mb
La prueba
>chisq.test(mb, correct=FALSE)
Observando el pValue Podemos afirmar que las características de la madre sí influyen en el estado del bebé.
Tabla de contingencia
Ejemplo
La empresa Frescos S.A. comercializa quesos de primera calidad, el gerente de ventas desea comparar el nivel de ventas semanal (en cientos de soles) de cuatro tipos de quesos. Para este fin, se realiza un experimento en el cual se selecciona al azar el registro de ventas de los diferentes tipos de queso que se ofrecen en seis tiendas con las que cuenta la empresa. Las ventas semanales registradas, se presentan a continuación:
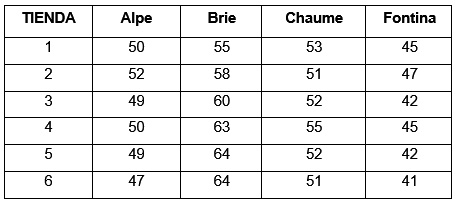
Construcción de una table de frecuencias para R
Paso 1:
Definimos los datos: Las frecuencias observadas, etiqueta de fila y de columna
>Venta = c(50, 52, 49, 50, 49, 47, 55, 58, 60, 63, 64, 64, 53, 51, 52, 55, 52, 51, 45, 47, 42, 45, 42, 41)
>Tienda = c( "Vea", "Metro", "Tottus", "Vivanda", "Wong","Minka","Vea", "Metro", "Tottus", "Vivanda", "Wong", "Minka", "Vea", "Metro", "Tottus", "Vivanda", "Wong", "Minka","Vea", "Metro", "Tottus", "Vivanda", "Wong", "Minka")
> Queso = c("Alpe", "Alpe", "Alpe", "Alpe", "Alpe", "Alpe", "Brie", "Brie", "Brie", "Brie", "Brie", "Brie", "Chaume", "Chaume", "Chaume", "Chaume", "Chaume", "Chaume", "Fontina", "Fontina", "Fontina", "Fontina", "Fontina", "Fontina")
Definimos un data frame (estructura tabular u hoja de datos)
>d=data.frame(Tienda,Queso,Venta)
La hipótesis a ser probada es: Las ventas de queso por tienda es independiente al tipo.
Vemos cómo queda la estructura tabular (table de contingencia)
>xtabs(Venta~.,d)
Lo guardaremos en una variable objeto tabla.
>tabla = xtabs(Venta~.,d)
>prop.table(tabla)
Se puede comprobar que todo esto suma 1
Podemos reducir los decimales a 4
>t = round(prop.table(tabla),4)
Ahora obtengamos los totals marginals
>addmargins(t)
Obtengamos los porcentajes (proporciones) condicionales por fila
>prop.table(tabla,1)
Si se suma horizontalmente se obtendrá 1.
Según los resultados podemos apreciar que el porcentaje de las ventas por tipo de queso no se diferencian, lo mismo ocurre por tienda. Esto significaría que, las ventas de queso por tienda, no depende del tipo de queso.
Porcentajes condicionales por columna
>prop.table(tabla,2)
Obtenemos la misma apreciación.
Ahora probaremos la hipótesis formulada con un nivel de significación del 5%.
>h = chisq.test(tabla)
>h
Como se puede ver, siendo pValue = 1, concluimos que las dos variables no están asociadas; es decir, son independientes.
Algunos resultados obtenidos con el test ChiCuadrado son:
>h$expected ## Las frecuencias esperadas >h$observed ## Las frecuencias observadas
Prueba de homogeneidad de proporciones
En este método de prueba, aplicado a una tabla de contingencia, se trata de comprobar si las muestras extraídas de una población homogénea son diferentes. Para ello se usa el criterio de proporcionalidad afirmando que las proporciones mostradas por una variable categórica es la misma que otra.
Ejemplo 7
En el estudio de un taller, se obtuvo un conjunto de datos para determinar si la proporción de artículos defectuosos producidos por los trabajadores era la misma durante el día, la tarde o la noche. Se encontraron los siguientes resultados luego de obtener muestras de trabajadores de diferentes turnos:
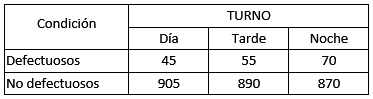
Utilice un nivel de significación del 5% para determinar si la proporción de artículos defectuosos no es la misma para los tres turnos.
Puesto que la prueba es la misma que en el caso de independencia de variables, definiremos una matriz, como en el ejemplo anterior.
> mdef=matrix(c(45, 95, 55, 890, 70, 870), nrow=2, ncol=3,dimnames=list(c("Def","NoDef"), c("Td","Tt","Tn")))
La prueba
>chisq.test(mdef,correct=FALSE)
Se prueba que hay diferencia significativa en la homogeneidad proporcional entre la condición del producto y el turno de producción.
Continuaremos en la siguiente sesión