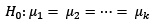
Modelo de diseño de un factor completamente aleatorizado

Modelo: Se desea comparar el rendimiento de k parcelas de cultivo, el rendimiento de trabajadores de tres turnos, las utilidades reportadas por k tipos de detergentes, la disminución de los niveles de colesterol debido a la aplicación de k tratamientos, etc.

La hipótesis nula:

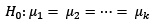
Ejemplo 1

Para estudiar el efecto que la marca de los cojintes tiene en la vibración del motor, se examinaron 5 marcas de cojinetes diferentes, instalando cada tipo de cojinete en muestras aleatorias distintas de 6 motores. Se recogieron la cantidad de vibración del motor (medida en micrones) cuando cada uno de los 30 motores estuvieron funcionando. Los datos de este estudio se muestran a continuación.

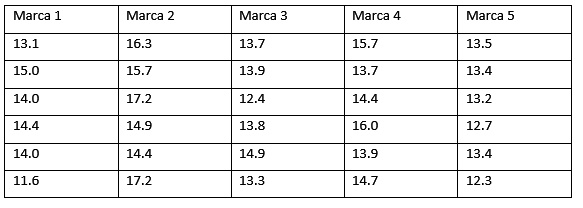
Definamos las dos variables: vib y marca

> vib =c(13.1, 15.0, 14.0, 14.4, 14.0, 11.6, 16.3, 15.7, 17.2, 14.9, 14.4, 17.2, 13.7, 13.9, 12.4, 13.8, 14.9, 13.3, 15.7, 13.7, 14.4, 16.0, 13.9, 14.7, 13.5, 13.4, 13.2, 12.7, 13.4, 12.3)
> marca=c("Marca 1","Marca 1","Marca 1","Marca 1","Marca 1","Marca 1","Marca 2","Marca 2","Marca 2","Marca 2","Marca 2","Marca 2","Marca 3","Marca 3","Marca 3","Marca 3","Marca 3","Marca 3","Marca 4","Marca 4","Marca 4","Marca 4","Marca 4","Marca 4","Marca 5","Marca 5","Marca 5","Marca 5","Marca 5","Marca 5")

Definiremos una estructura de data frame

>df = data.frame(vib, marca)
>df

Obtenemos el anova usando la función aov(), lo dejamos en av, y el pValue, con el resumen.

>av = aov(vib~marca, data = df)
>av

Visualicemos el resumen

>summary(av)

Puesto que se rechaza la hipótesis nula, entonces existe diferencia significativa en por lo menos dos marcas. Pero estos resultados serán válidos siempre que los residuales satisfacen los tres supuestos:

- Normalidad
- Homocedasticidad de la varianza
- Prueba de independencia
 

Para la prueba de normalidad usaremos la prueba de Shapiro – Wilks mediante la función shapiro.test aplicado a los residuales del anova anterior

>shapiro.test(residuals(av))
Satisface el primer supuesto.

Para la prueba de homocedasticidad de las varianzas usaremos la prueba de Bartlett

>bartlett.test(vib~marca, data = df)

Con pValue = 0.3931, podemos afirmar que las varianzas son iguales, en consecuencia, se satisface este supuesto.

Para la prueba de independencia, debemos definir 5 vectores columna a fin de presentar el diagrama de dispersión

>m1=vib[1:6]
> m2=vib[7:12]
> m3=vib[13:18]
> m4=vib[19:24]
>m5=vib[25:30]

Ahora el diagrama de dispersiòn

> pairs(m1~m2+m3+m4+m5)

En consecuencia, la aplicación del método es válido.

Ahora bien, ¿Cuáles son los pares de medias en los que se presenta la diferencia significativa?

Esto significa realizar pruebas de pares de igualdad de medias. Para ello debemos utilizar la prueba de la mínima diferencia significativa LSD.test, que está incluida en el paquete agricolae.

Instalemos el paquete y luego lo cargamos a memoria.

>library(agricolae)

Realizamos la prueba

> grupos =LSD.test(y = av, trt = "marca", group = T, console = T)

Esto nos indica que las 5 marcas forman 3 grupos. La marca 2 no forma grupo; las marcas 1, 3 y 4 forman el grupo b; las marcas 1, 3 y 5 forman el tercer grupo. Esto significa que, las marcas del mismo grupo no difieren significativamente.

Un resultado más sencillo de interpretar lo obtenemos usando la opción group = F

> res=LSD.test(y = av, trt = "marca", group = F, console = T)
 

Ejemplo 2

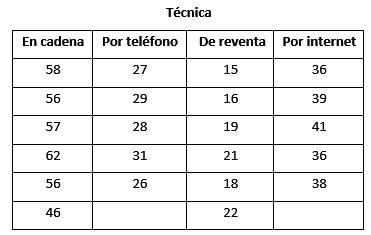
Con el objetivo de incrementar sus ganancias la empresa Original S.A., realiza un programa de capacitación en técnicas de ventas para sus colaboradores. Después de culminado el programa se comparan cuatro técnicas de ventas en términos del valor de las ventas realizadas (en cientos de soles). A continuación, se presentan las ventas realizadas por 22 de los colaboradores de Original S.A., los cuales previamente fueron asignados aleatoriamente para que sean capacitados en una de las técnicas de ventas.

Pruebe los supuestos del modelo aditivo lineal.

Realice la prueba más adecuada para responder si existe diferencia en la efectividad de las cuatro técnicas de ventas. Use   0.03.

Definamos los vectores relativos a venta y técnica (vta, tec)

>vta = c(58, 56, 57, 62, 56, 46, 27, 29, 28, 31, 26, 15, 16, 19, 21, 18, 22, 36, 39, 41, 36, 38) > tec = c("Cad", "Cad", "Cad", "Cad", "Cad", "Cad", "Tel", "Tel", "Tel", "Tel", "Tel", "Rev", "Rev", "Rev", "Rev", "Rev", "Rev", "Int", "Int", "Int", "Int", "Int")
 

Sin definir una estructura de data frame, realizaremos el cálculo del anova.

>av = aov(vta~tec)
>av
>summary(av)
<

Probemos si cumple con el supuesto de normalidad de residuos

> shapiro.test(residuals(av))
Se cumple con este supuesto
El de homogeneidad de varianzas
> bartlett.test(vta~tec)
< También se cumple con este supuesto.

Volviendo a obtener el anova

> av
>summary(av)

En consecuencia, podemos afirmar que sí existe diferencia significativa entre las diferentes técnicas de venta.

Para saber entre cuáles se presenta la diferencia realizaremos la prueba de LSD.test con la opción group = F.
> res=LSD.test(y = av, trt = "tec", group = F, console = T)

Podemos comprobar, que todas las técnicas difieren significativamente.

Usando el método de intervalos de Tukey:

> plot(TukeyHSD(av,"tec"))

 

Modelo de diseño por bloques aleatorizados

En este modelo se dispone de un grupo de k muestras diferenciadas por el tipo de tratamiento aplicadas y agrupadas en bloques aleatorios. En este caso se puede probar dos tipos de hipótesis nulas: la igualdad en el promedio de los tratamientos y entre los bloques.

Ejemplo 3

La empresa Frescos S.A. comercializa quesos de primera calidad, el gerente de ventas desea comparar el nivel de ventas semanal (en cientos de soles) de cuatro tipos de quesos. Para este fin, se realiza un experimento en el cual se selecciona al azar el registro de ventas de los diferentes tipos de queso que se ofrecen en seis tiendas con las que cuenta la empresa. Las ventas semanales registradas, se presentan a continuación:

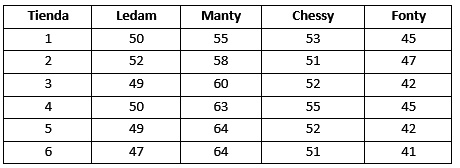
a) Con el 5% de significación, ¿cree usted que el tipo de queso influye en las ventas semanales?
b) Con el 5% de significación, ¿cree usted que las ventas semanales de queso, difiere entre las tiendas?

Analizaremos el caso a)

>vta=c(50, 52, 49, 50, 49, 47, 55, 58, 60, 63, 64, 64, 53, 51, 52, 55, 52, 51, 45, 47, 42, 45, 42, 41) > tda = c("Tda 1", "Tda 2", "Tda 3", "Tda 4", "Tda 5", "Tda 6", "Tda 1", "Tda 2", "Tda 3", "Tda 4", "Tda 5", "Tda 6", "Tda 1", "Tda 2", "Tda 3", "Tda 4", "Tda 5", "Tda 6", "Tda 1", "Tda 2", "Tda 3", "Tda 4", "Tda 5", "Tda 6") > que=c("Ledam", "Ledam", "Ledam", "Ledam", "Ledam", "Ledam", "Manty", "Manty", "Manty", "Manty", "Manty", "Manty", "Chessy", "Chessy", "Chessy", "Chessy", "Chessy", "Chessy", "Fonty", "Fonty", "Fonty", "Fonty", "Fonty", "Fonty")

Obtengamos el anova

>av = aov(vta~tda+que)
< >av
>summary(av)

Si deseamos estimar el modelo aditivo, debemos usar el siguiente procedimiento:

> mod=lm(vta~tda+que)
>mod

El anova

>av = aov(mod)
>av
>summary(av)

Antes de responder las dos preguntas, veamos si se satisface los dos supuestos de modelo:

Prueba de la normalidad

> shapiro.test(residuals(av))

Prueba de homocedasticidad, en ambos casos

> bartlett.test(vta~que)
> bartlett.test(vta~tda)

Como en un ejemplo anterior, para la prueba de independencia, definiremos vectores correspondientes a los 4 quesos y analizar sus respectivos diagramas de dispersión por parejas.

> q1=vta[1:6]
> q2=vta[7:12]
> q3=vta[13:18]
> q4=vta[19:24]
>pairs(q1~q2+q3+q4
 

Puesto que se satisfice los tres supuestos, podemos afirmar lo siguiente:

Al 5% de significación, no existe diferencia significativa en la venta semanal de queso por tienda ya que pValue = 0.693; sin embargo, las ventas entre los tipos de queso, sí existe diferencia significativa.

Comparaciones múltimples de medias

> grupos = LSD.test(y=av, trt = "tda", group = T, console = T)

Hay un solo grupo; es decir,

Para visualizar los intervalos de confianza

> grupo = LSD.test(y=av, trt = "tda", group = F, console = T)

Se comprueba que no hay diferencia significativa en la venta semanal entre las tiendas

Modifiquemos el criterio

> grupo = LSD.test(y=av, trt = "tda", group = T, console = T)

Cambiando la modalidad del argumento group:

> grupo = LSD.test(y=av, trt = "que", group = T, console = T)

Usando la prueba de Tukey:

>plot(TukeyHSD(av,"a"))
 

Modelo de diseño por bloques con replicación

En este modelo, cada uno de los bloques se replican; es decir, repiten r veces y pueden formulares pruebas respecto a los bloques y los tratamientos, así como con las interacciones de bloques y tratamientos.

Ejemplo 5

Se analiza el efecto de tres venenos y cuatro antídotos en el tiempo de supervivencia de las ratas. La muestra consta de 4 replicaciones por cada tipo de veneno y antídoto. El tamaño de la gran muestra será de 4x3x4 = 48. Los datos se encuentran en el archivo antídoto.txt que se encuentra en la careta datos.

La imagen siguiente muestra la disposición de los datos, forma en la que fueron grabados en el archivo plano.

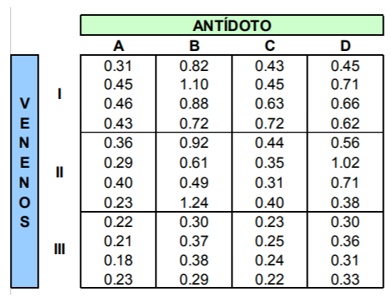
> d=read.table("c:\\tempo1\\antidoto.txt",sep = ",", head = T)
>d

Definiremos los vectores antídoto (a) y veneno (v)

> a=c("A", "A", "A", "A", "A", "A", "A", "A", "A", "A", "A", "A", "B", "B", "B", "B", "B", "B", "B", "B", "B", "B", "B", "B", "C", "C", "C", "C", "C", "C", "C", "C", "C", "C", "C", "C", "D", "D", "D", "D", "D", "D", "D", "D", "D", "D", "D", "D")
> v=c("I","I","I","I","II","II","II","II","III","III","III","III", "I","I","I","I","II","II","II","II","III","III","III","III", "I","I","I","I","II","II","II","II","III","III","III","III", "I","I","I","I","II","II","II","II","III","III","III","III")

Un data frame confirmará la forma de ingresar los datos
> df = data.frame(a,v,d)

Obtenemos el análisis de vaianza del modelo. Para ello, la estructura que tiene d no es adecuado, debe tener la estructura de vecor, como lo son los antídotos (a) y veneno (v). Para ello, vamos a extraer las últimas 4 columnas de d hacia una nueva variable vecor.

> t=c(d[,1],d[,2],d[,3],d[,4])

El anova:

>av = aov(t~v+a)
>summary(av)

Podemos observar que se rechaza las dos hipótesis; es decir, existe diferencia significativa en el tiempo de acción entre los tipos de veneno y antídoto.

Los coeficientes del modelo se estiman usando

> model.tables(av,"means")

Tomando en cuenta las medias o también los efectos "effects".

Comparaciones múltiples de medias usando Tukey

Para el veneno:

> TukeyHSD(av,"v")

No hay diferencia signficativa entre los venenos I y II.

Del mismo modo, entre los antídotos

> TukeyHSD(av,"a")

No hay diferencia significativa entre A con B y el antídoto B con C y D.

Observando los intervalos

Entre los venenos

> plot(TukeyHSD(av,"v"))

Entre los antídotos:

> plot(TukeyHSD(av,"a"))

Hay diferencia significativa entre los antídotos A con B, A con D y C con D.

Continuaremos en la siguiente sesión