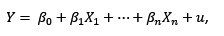
Dado el modelo

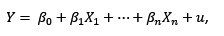
se trata de obtener una recta de regresión estimada

En R, la función que permite estimar dichos parámetros es:

>lm(fórmula, data, subset, weights, na.action, method = “qr”, model = TRUE, x=FALSE, y=FALSE, qr = TRUE, singular.ok = TRUE, contrasts = NULL, offset, …)

donde

fórmula: Es una expresión que define las variables del modelo Y ~ X; es decir, Y = f(X).
data: Lista o data.frame conteniendo las variables del modelo
subset: Vector opcional que puede ser usado en el proceso de ajuste
weights: Vector opcional como el anterior. Si es NULL se usa el método MCO
 

Ejemplo 1

Los siguientes datos corresponden a diferentes cajas ubicados a diferente distancia y el objetivo es estimar el tiempo requerido para organizarlas.

La siguiente dirección de Internet contiene el archivo:

http://www.diegocalvo.es/wp-content/uploads/2016/09/datos-regresion-lineal-multiple.txt

Usando read.table, lo capturaremos

Para probar, vamos a leer datos de la página: icedat.com/macros/agri.txt. Este archivo no tiene cabecera:

> agri = read.table("http://www.icedat.com/macros/agri.txt") >agri

Para el desarrollo debemos leer el archivo datos-regresion-lineal-multiple.txt de la dirección anterior.

>d=read.table("http://www.diegocalvo.es/wp-content/uploads/2016/09/datos-regresion-lineal-multiple.txt", header = TRUE)
>d

Podemos apreciar que se trata de un problema de tres variables.

Veamos el diagrama de dispersión de las tres variables

>pairs(d)

Apreciamos que las variables Tiempo y NroCajas tienen relación; sin embargo, con la Distancia podría haber una relación con una correlación muy baja. Lo comprobamos usando

>cor(d)

En efecto, hay un 72.46% de dependencia entre Tiempo y NroCajas y sólo el 40.53%, éstas con Distancia. Para un estudio más completo analizaremos los dos modelos:

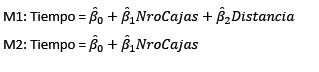
Ajustemos el primer modelo:

>M1=lm(d$Tiempo~d$N_cajas+d$Distancia, data=d)
>M1
>summary(M1)

El modelo estimado es: Tiempo = 2.3112 + 0.8772NroCajas + 0.4559Distancia + e

Puesto que, siendo R² = 7368, indica que el 26.3% de la variabilidad del Tiempo no se encuentra explicado por las otras dos variables, quitemos la variable que tiene menor correlación con el tiempo y generemos el modelo 2, M2.

>M2=lm(d$Tiempo~d$N_cajas, data=d)
>summary(M2)

Observamos que el primer modelo explica mejor el problema.

Una forma de comparar modelos de regresión, es mediante un ANOVA entre los modelos y, el que tenga un pValue menor que α, será descartado.

>anova(M2,M1)

Esto indica que el modelo M1 explica mejor.

Podemos realizar un análisis de residuos para comprobar la confiabilidad del modelo. Esto significa que debemos probar los tres supuestos:

- Prueba de normalidad
- La homocedasticidad. La varianza de los errores es constante
- Independencia de los errores
-

Primer supuesto:

Generación de los residuales

>res=rstandard(M1)

Obtención de una ventana particular

>win.graph()

Dividimos la ventana en una fila con tres columnas

>par(mfrow=c(1,3))

Gráfica de histograma de los residuales

>hist(res)

Diagrama de caja para los residuales

>boxplot(res)

Gráfico de los cuantiles para ajustarlo a una línea

>qqnorm(res)

Finalmente la recta en el gráfico anterior

>qqline(res)
 

Segundo supuesto:

Para probar la homocedasticidad, debemos tener un gráfico en donde los residuales estandarizados y los valores estimados se ajusten a uno y otro lado de una recta horizontal.

Obtención de los valores ajustados

>est=fitted.values(M1)

Ploteamos los dos vectores

> plot(est,res,xlab="Valores estimados",ylab="Residuales estandarizados")

>abline(h=0)

Tercer supuesto

Podemos probar la independencia de los errores usando el coeficiente de correlación

>cor(res,d$N_cajas)
>cor(res,d$Distancia)

Lo veremos mediante un ploteo de los residuales y las dos variables independientes

>plot(d$N_cajas,res,xlab="Nro cajas",ylab="Residuales estandarizados")
>plot(d$Distancia,res,xlab="Nro cajas",ylab="Residuales estandarizados")

 

Ejemplo 2

Veamos el problema del volumen de producción agrícola, datos contenidos en agri.xlsx

Carguemos el paquete xlsx

Vamos a cargar el archivo agri.xlsx

>dag=read.xlsx("c:\\datosr\\agri.xlsx",1)

(Puesto que antes ya hemos instalados el paquete xlsx, podemos cargarlo usando

>library(xlsx)

Estadísticas:

>summary(dag)

Veamos el gráfico de dispersión
Gráfico de dispersión entre ProdAg y VolFit
>qplot(ProdAg,VolFit,data=dag)

(Si no está la función qplot(), debemos cargarla la librería ggplot2 usando: library(ggplot2) )

>qplot(ProdAg,VolFit,data=d,color=ModoFin)

Un histograma de ProdAg

>qplot(ProdAg,data=dag,color=ModoFin,bins=5)
 

Diagrama de dispersión de todas las variables numéricas.

>pairs(dag)
 

La matriz de correlación

>cor(matrix(c(dag$ProdAg,dag$VolFit,dag$MaqAgr,dag$Finan),20,4))
 

Descartando la última variable, que es dicotómica, estimaremos un modelo de regresión:

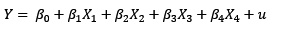
> reg=lm(dag$ProdAg~dag$VolFit+dag$MaqAgr+dag$Finan, data=dag)
>reg

El modelo estimado es:

ProdAg = 166164.177 + 69.797VolFit – 0.707MaqAgr + 2.077Finan = e
>summary(reg)

La table ANOVA

>anova(reg)

Los intervalos de confianza, a un nivel del 95%

>confint(reg, level = 0.95)

Ejemplo 3

Una empresa fabricante de cereales está interesada en conocer cómo afecta a las ventas del producto, la publicidad en la televisión, en la radio y en los periódicos. Para ello, realiza un estudio de los gastos mensuales (en miles de euros) correspondientes a los últimos 20 meses.

Estos datos se presentan en la tabla que se encuentra en el archivo cereales.xlsx.

Leemos los datos hacia el objeto datos.

>datos=read.xlsx(“c\\datosr\\cereales.xlsx”,1)

Podemos visualizar los datos.

Definiremos un data.frame para emitir un diagrama de dispersión de todos los pares de variables

>df = data.frame(datos)
 

Ahora lo ploteamos

>plot(df)

Como se puede apreciar, existe bastante sospecha de que la publicidad en los diferentes medios, influyen en la ventas de cereales.

Lo mismo nos dice la matriz de correlaciones

>cor(df)
<´>Realicemos la estimación

> vest=lm(Ventas~Pubtv*Pubra*Pubper, data=datos)
>vest

Veamos otros cálculos

>summary(vest)
 

Podemos plotear el modelo

>plot(Ventas~Pubtv*Pubra*Pubper, data=datos)

Haciendo clic en el gráfico podemos observar los otros diagramas de dispersión.

Veamos el ajuste de Ventas y Pubtv

> esttv=lm(Ventas~Pubtv, data=datos)

Su gráfico de dispersión

> plot(datos$Ventas,datos$Pubtv)
La recta de ajuste
>abline(esttv)
 

Ahora veamos los gráficos de los residuales, los valores estimados, los residuales estandarizados. Para ello se debe hacer clic en la ventana de gráficos.

>plot(esttv)          # Se debe hacer clic en la ventana de gráficos
 

Los gráficos 2 y 4 permiten contrastar gráficamente la homocedasticidad y normalidad de los residuos. Teóricamente, los puntos deben estar dispersos aleatoriamente en toda la gráfica.

La prueba de normalidad se puede completar con la prueba de normalidad de Kolmogorov-Smirnov: ks.test(x, distrib)

En esta prueba, x representa los residuales del modelo y distribución de frecuencias que, en este caso, usaremos la distribución normal (pnorm).

> ks.test(esttv$residuals,"pnorm")

Continuaremos en la siguiente sesión