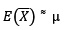
Si X ---> N(µ,σ²), entonces
fx=f(x)=dnrom(x,µ,σ)
Fx=F(x)=P(X ≤x)=pnorm(x,µ,σ)
P(X ≥a )=pnorm(a,µ,σ)
Si se desea generar p números aleatorios con distribución N(µ,σ²):
>p=30
>r=rnorm(p, µ,σ)
Ejemplo 1
>u=0
>z=1
>x=seq(-4,4,0.05)
>fx=dnorm(x,u,z)
>Fx=pnorm(x,u,z)
>df =data.frame(x,fx,Fx)
>plot(df)
La función curve(..) nos permite graficar con mayor precisión
>x=seq(-4,4,0.05)
> curve(dnorm(x,0,1),xlim=c(-4,4),col="blue",lwd=2, xlab="x",ylab="f(x)", main="Función de densidad N(0,1)")
Nota:
El parámetro “lwd” permite definir el grosor de la curva.
Ejemplo 2
El ingreso mensual promedio de los médicos del MinSa es de 5609 soles con una desviación de 146 soles. Si se supone que los ingresos mensuales tienen distribución normal,
Construya la gráfica de la distribución
Encuentre la probabilidad de que los ingresos de un determinado, médico se encuentre entre 5200 y 5800 soles.
Grafique la probabilidad anterior
Solución
Generemos valores de X desde µ - 4σ hasta µ + 4σ.
>u=5609
>z=146
>x=seq(u-4*z,u+4*z,10)
> fx=dnorm(x,u,z)
>plot(data.frame(x,fx))
Debemos hallar P(5200 < X < 5800)
P(5200 < X < 5800) = F(5800) – F(5200)
>Prob = pnorm(5800,u,z)-pnorm(5200,u,z)
La gráfica pedida:
Generamos todos los puntos dentro del intervalo (5200, 5800)
> reg=seq(5200,5800,0.2)
Ahora los puntos sobre el eje X que representa la base del polígono
> xp=c(5200,reg, 5800)
Los puntos que representan las alturas de cada punto del eje X
> yp=c(0,dnorm(reg,u,z),0)
Ahora trazamos la curva
>curve(dnorm(x,u,z),xlim=c(5025,6193),yaxs="i",ylim=c(0,0.0035),ylab="f(x)", main="N(5609,146")
Finalmente el polígono
> polygon(xp,yp,col="red")
Ejemplo 3
Usaremos cbind y mplot para mostrar la gráfica de la normal para diferentes valores de sus parámetros.
cbind: permite arreglar a un vector, matriz o data.frame en filas y columnas. matplot: permite plotear columnas de una matriz
Definamos el vector x que toma valores desde -6 hasta 6 en un total de 100 valores.
>x =seq ( -6, 6, len=100 )
Puesto que dnorm(x, media, desvstand) genera un conjunto de valores normales según la longitud de x, podemos definir un vector usando cbind.
>y=cbind (dnorm( x, -2,1 ),dnorm (x, 0,2 ),dnorm ( x, 0, .5), dnorm ( x, 2, .3 ), dnorm ( x, -.5, 3 ) )
Ahora vamos a plotear a x e y, matricialmente, por ello hemos definido usando cbind.
> matplot ( x, y, type="l", col=c("red","blue","green","magenta","black") )
Ahora la función que permite ubicar la leyenda en la ventana: El cuadro de la leyenda se ubicará en la posición (-6,1.3) en el cual se mostrará para la primera gráfica: mu = -2 y desv = 1; para la segunda: mu = 0, con desv = 2; etc.
Trazaremos un grupo de valores que representan la leyenda de estos gráficos.
> legend ( -6, 1.3, paste ("mu =", c(-2,0,0,2,-.5),"; sigma =", c(1,2,.5,.3,3) ), lty=1:5, col=1, cex=.75 )
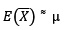
Teorema del Limite Central
Sea X1, X2, …, Xn una muestra aleatoria extraída de una población con media µ y varianza σ². Si S= ∑Xi entonces, para un tamaño de muestra, suficientemente grande, S ---> N(µS y σ²S) donde µS=E(S)= ∑µ_i y SS2 = ∑σi2. En particular, si S= ¯(X,) entonces E(S)=E(¯X)= µ.
Verificación del teorema
Supongamos que en Pisco se tiene registrada una población de 10000 lobos de mar, cuyo peso promedio deseamos estimar. Supongamos que los pesos varían desde 200 a 800 Kg.
Extraeremos muestras de tamaño 50 y calcularemos la media de cada muestra. Luego calcularemos la media de estas medias muestrales y su varianza muestral. Debemos esperar que la media muestral de medias 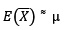
Verificación del teorema
Supongamos que en Pisco se tiene registrada una población de 10000 lobos de mar, cuyo peso promedio deseamos estimar. Supongamos que los pesos varían desde 200 a 800 Kg.
Extraeremos muestras de tamaño 50 y calcularemos la media de cada muestra. Luego calcularemos la media de estas medias muestrales y su varianza muestral. Debemos esperar que la media muestral de medias E(¯X) ͌ µ
Generemos una población de 10000 pesos de lobos marinos
>P=sample(200:800,10000,rep=T)
Siendo esta la población, por censo calculamos su media y varianza poblacionales:
>u=mean(P)
>z=sqrt(var(P))
Vamos a construir una función que nos permita obtener la media de m muestras de tamaño n:
>mm=function(n) {
mu = mean(sample(P,50,rep=T))
return (mu)
}
Ahora la llamaremos m=30 veces y lo dejaremos en el vector medmuestral
> medmuestral=replicate(30,mm(50))
>medmuestral
Ahora calculemos la media de estas medias muestrales
>xbarra = mean(medmuestral)
>xbarra
Comparemos con µ la media poblacional
En mi caso: xbarra = 499.1453 y u = 499.2035.
Calculemos su desviación estándar
>desv=sqrt(var(medmuestral))
>
Volvamos a calcular la media muestral y la varianza muestral de otra serie de 50 medias muestrales
> medmuestral=replicate(50,mm(50))
> xbarra = mean(medmuestral)
>desv=sqrt(var(medmuestral))
Se puede comprobar que la desviación obtenida se aproxima a σ/√n
Esta es la forma de aplicar el Bootstrapping.
Continuaremos en la siguiente sesión