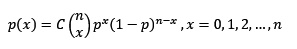
Podemos crear variables aleatorias simples usando las funciones sample() y runif()<.
>x=sample(0:20,50,rep=T)
>y=runif(50,0,1)
Podemos disponer de una distribución tabular usando data frame
> p = data.frame(x,y)
>p
>plot(p)
Adicional
Gráficos con plot() para dos variables
Sintaxis:
>plot(x,y,type=”..”,main=”..”,xlab=”..”,ylab=”..”)
Donde type:
l=línea, p=puntos, b=ambos, h=histograma, s=escalera, o=overplotted
main=título, xlab=Texto en el eje X, ylab=Texto en el eje Y
>x=-5:5
>y=x**2
>plot(x,y)
> plot(x,y,"l")
Se puede usar también
>plot(x,y,type = ”l”)
>y= 5*x**3+3*x**2-10
>plot(x,y,”p”,main=”Gráfica de y=5x**3+3x**2-10”,xlab=”X”,ylab=”Y”)
También podemos usar la función curve() para trazar el gráfico de manera más refinada.
>x=2
>curve(x**2,from=-4,to=4)
>curve(sin,from=-2*pi,to=2*pi)
>curve(x**2-sqrt(x)+x-3,from=0,to=5)
>text(2.5,20,"f(x) = x**2-sqrt(x)+x-3")
Grafiquemos otra vez
> curve(x**2-sqrt(x)+x-3,from=0,to=5)
Otro tipo de texto
> text(2.5,20,expression(x**2-sqrt(x)+x-3))
Observación importante
Cuando hablamos de variables aleatorias, estamos hablando de sus funciones de densidad o de probabilidad y sus funciones de distribución acumulada.
En R se dispone de las siguientes funciones en cada variable aleatoria conocida:
dnamed (x, tamaño, prob, log = FALSE)
pnamed (q, tamaño, prob, lower.tail = TRUE, log.p = FALSE)
qnamed (p, tamaño, prob, lower.tail = TRUE, log.p = FALSE)
Rnamed (n, tamaño, prob)
donde "named" debe reemplazarse por
binom: En el caso de la distribucion Binomial
pois : En el caso de la distribución de Poisson
hyper: En el caso de la distribución Hiperogeométrica
exp : En el caso de la distribución Exponencial
norm : En el caso de la distribución Normal, etc.
La primera genera la función de probabilidad o de densidad
La segunda es la función de distribución acumulada
La tercera usa los valores de los cuantiles
La cuarta genera una secuencia de valores aleatorios que siguen la distribución indicada por named.
Distribución Binomial
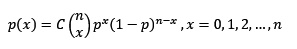
Ejemplo 1
Obtenga la distribución de probabilidad del número de veces que sale cara cuando se lanza una moneda 3 veces
>x=0:3
>p=dbinom(x,3,0.5)
>pac=pbinom(x,2,0.5)
Veamos la table de la distribución de probabilidad: p(x) = P(X = x)
>dp=data.frame(x,p) >dp
Gráfica
>plot(dp)
>barplot(p)
Una tabla que contenga, x, f(x) y F(x)
>fx= dbinom(x,3,0.5)
>Fx=pbinom(x,3,0.5)
>px=data.frame(x,fx,Fx)
La función de probabilidad por definición:
>n=3
>x=0:3
>p=0.5
>fx=choose(n,x)*p**x*(1-p)**(n-x)
Ejemplo 2
Sea X una variable aleatoria tal que X ---> B(n=10, p = 0.4)
La función de densidad:
> fx=dbinom(x,n,p)
La función de distribución acumulada
> Fx=pbinom(x,n,p)
Gráfica de la función de probabilidad
> plot(fx,type="h",xlab="x",ylab="P(X=x)",main="Gráfica de la función de probabilidad")
Gráfica de la función de probabilidad acumulada Fx
> Fx=pbinom(0:11,10,0.4)
Observe que le asignamos un valor más a X a fin de visualizar el máximo valor de probabilidad acumulada.
Otro gráfico en la misma ventana
>par(new=T)
> plot(Fx,type="h",xlab="x",ylab="P(X=x)",col = "red")
Cambiemos el tipo de gráfico
> plot(fx,type="b",xlab="x",ylab="P(X=x)",col="blue",main="Gráfica de la función de probabilidad")
> plot(Fx,type="b",xlab="x",ylab="P(X=x)",col = "red")
Otra forma de graficar Fx en escalones
>plot(stepfun(0:10,Fx),xlab="x",ylab="P(X=x)",main="Gráfica de la función de probabilidad")
Ejemplo 3
Generar una distribución para X----> B(n = 10, p = 0.5) y luego graficar las funciones de probabilidad y de distribución.
Recordando la sintaxis de la función de probabilidad
>x=0:10
>n=10
>p = 0.25
>fx=dbinom(x,n,p)
>Fx=pbinom(x,n,p)
Sus gráficas
>dbf=data.frame(x,fx)
>dbF=data.frame(x,Fx)
> plot(dbf,col="blue",type="l")
>par(new=T)
> plot(dbF,col="red",type="l")
> barplot(fx,col="blue")
> par(new=T)
> barplot(Fx,col="red")
Distribución de Poisson
Sea X ---> P(lambda), con x =0,1,2,….
Su función de probabilidad viene dada por
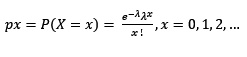
A una caseta de peaje llegan 15 vehículos cada media hora. Obtenga las distribuciones de probabilidad del número de vehículos que llegará cada hora.
Si definimos a X como : “El número de vehículos que llegarán cada hora”, entonces X tiene distribución de Poisson cuyo parámetro lambda es 30.
En este caso, siendo lambda = 30, su función de probabilidad viene dada por
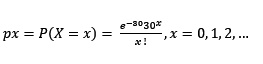
>x=0:50
>lambda=30
>fx=dpois(x,lambda)
>Fx=ppois(x,lambda)
>plot(fx)
>par(new=T)
>plot(Fx)
Distribución Hipergeométrica
De una población de tamaño N, k de los cuales tienen cierto atributo, se extrae una muestra de tamaño n. Si X representa el número de elementos en la muestra que tienen el atributo, entonces X ---> H(N,k,n) . Si m = N-k, la función de probabilidad viene dada por dhyper(x,n,m,k).
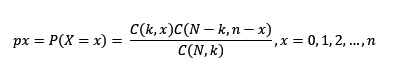
Los valores de x:
>x=0:n
>N=25
>k=5
>n = 4
>m = 20; # m = N-k
Luego
> fx = dhyper(x,k,m,n)
Su función de distribución acumulada
> Fx = phyper(x,k,m,n)
Distribución exponencial
Si X ---> E(beta), donde el parámetro beta = 1/mu. (mu = media)
Las funciones de densidad y acumulada:
>fx=dexp(x,rate=1/ µ,lower.tail=TRUE)
Si lower.tail=TRUE, se calcula P(X≤x), en caso contrario, P(X>x).
Ejemplo
El número de nacimientos que se producen en Lima, anualmente es de 3090. Si la distribución del número de nacimientos puede ajustarse a una distribución exponencial, encuentre
a) La probabilidad de que, el próximo año se produzcan, a lo más, 3500 nacimientos
b) La probabilidad de que, el próximo año se produzcan por lo menos 4000 nacimientos
c) ¿Cuántos nacimientos, a lo más, se producirá el próximo año, con probabilidad 0.50?
Solución
Sea X: Nro de nacimientos por año, en miles. Parámetro beta = 1/3.09
X E(1/3.09)
a)>pexp(3.5,1/3.09,lower.tail=TRUE)
b)>beta=1/3.09
>pexp(4,beta,lower.tail=FALSE)
c)>qexp(0.5,beta,lower.tail=TRUE)
Distribución normal
Continuaremos en la siguiente sesión