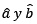 son los estimadores de a y b, entonces
son los estimadores de a y b, entonces 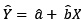 será la ecuación estimada.
será la ecuación estimada.Dado el modelo lineal Y = a + bX + e, estamos interesados en estimar por mínimos cuadrados los coeficientes de regresión a y b tal que, si 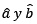 son los estimadores de a y b, entonces
son los estimadores de a y b, entonces 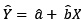 será la ecuación estimada.
será la ecuación estimada.
Si eb es el vector columna 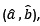 los valores de dichos estimadores lo hallaremos por el método de los mínimos cuadrados.
los valores de dichos estimadores lo hallaremos por el método de los mínimos cuadrados.
Dado y = a + bx, matricialmente,
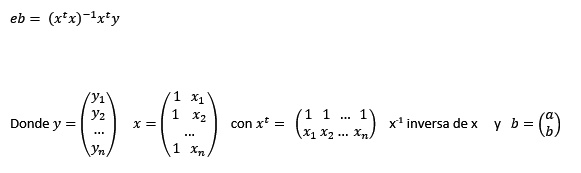
Ejemplo 1
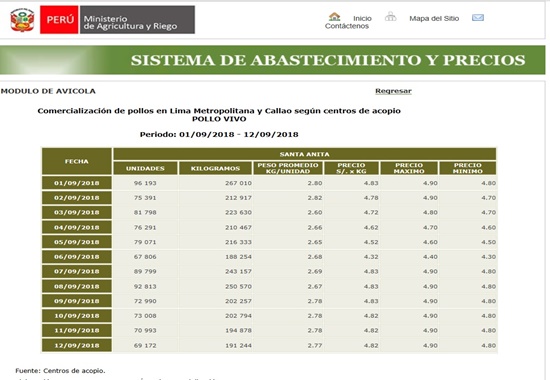
Como un ejemplo para regresiones, supongamos que tenemos una muestra sobre la venta de pollos en Santa Anita entre el 1 y 12 de Setiembre del 2018 (ver imagen).
>prPollo=c(4.83,4.78,4.72,4.62,4.52,4.32,4.83,4.83,4.83,4.82,4.82,4.82)
Cantidad de pollo en miles:
>canPollo=c(96.193,75.391,81.798,76.291,79.071,67.806,89.799,92.813,72.990,73.008,70.993,69.172)
Diagrama de dispersión (pairs(…))
Una manera de saber si existe o no una relación entre estas dos variables es trazando un diagrama de dispersión, que, en el caso del R, se tiene la función pairs(objeto).
Sintaxis:
>pairs(x,labels)
Donde x es una secuencia de variables o un data.frame y labels un vector de nombres de variables. Un data.frame es un ordenamiento rectangular, similar a una matriz. A diferencia de ella, en la cual todo su contenido es de tipo numérico, en un data.frame su contenido puede tener distintos tipos de datos, columnas numéricas o de cadena.
>pairs(canPollo~prPollo) #
>pairs(prPollo~canPollo)
Definamos un data.frame con los datos
>df=data.frame(canPollo,prPollo)
Pueden visualizar su contenido, similar a una matriz de 12x2
>pairs(df)
Ahora vamos a definir etiquetas para no usar los nombres de las variables
> et=c("Cantidad","Precio")
Graficamos
>pairs(df,labels=et)
Por último, respecto a diagramas de dispersión, usemos otros datos, el iris del R:
Observando la data
>str(iris)
podemos preguntarnos si existe alguna relación entre la longitud y amplitud de los pétalos y los sépalos. Para ello podemos construir un diagrama de dispersión de las 4 primeras variables:
> pairs(iris[1:4])
Trazando la nube de puntos con diferente color:
> pairs(iris[1:4],bg = c("red", "orange", "blue")[unclass(iris$Species)])
> pairs(iris[1:4], main = "Diagrama de dispersion. Largo vs ancho", col = c("red", "green", "blue"))
> pairs(iris[1:4], main = "Datos de Iris con 3 especies", pch = 21, bg = c("red", "orange", "blue") [unclass (iris$Species)])
Ahora vamos a estimar una regresión lineal para el problema de los pollos.
En el caso de problemas de regresión, nos gustaría disponer de estos datos en una matriz A de 12x2. Esto lo obtenemos con
>a=matrix(c(prPollo, canPollo),ncol=2)
o también
> a=matrix(c(prPollo, canPollo),12,2)
Ahora hallamos la transpuesta de a, con
>ta = t(a)
Si se desea estimar los regresores en una recta de regresión, debemos obtener la inversa de la transpuesta de a, por a, es decir, ta por a. Para ello:
>taxa = ta%*%a
>taxa
Hallamos su inversa
>solve(taxa)
Si la ecuación de regresión es y = a + bx, donde a y b son los coeficientes de regresión, en el caso de los datos de los pollos los coeficientes, usando matrices serán: 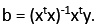
Para ello:
>y = prPollo
Construyamos la matriz x, de acuerdo a la definición. La primera columna tiene 12 unos, la segunda debe ser canPollo.
> x1=sample(1:1,12,rep=T)
>x2=canPollo
> x=matrix(c(x1,x2),12,2)
>x
Obtenemos la transpuesta de x y lo dejamos en tx
>tx = t(x)
>tx
Resolvemos todo a la vez
> b=solve(tx%*%x)%*%(tx%*%y)
El vector columna contiene los estimadores de a y b en Y = a + bX
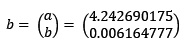
Luego la ecuación estimada es: Y = 4.242690175 + 0.006164777 X
Otras estadísticas:
>yprom = mean(prPollo)
>xprom = mean(canPollo)
Covarianza: >cov(prPollo,canPollo)
CoefCorr = ro = cov(prPollo,canPollo)/sqrt(var(prPollo)*var(canPollo))
>CoefCorr
Obtención de la varianza de los errores (residuales)
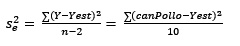
Como
Si k es el número de variables independientes, entonces
>k = 1
Obtención de los precios estimados (yest)
> yest = b[1]+b[2]*canPollo # y = a + bX

Uso de la librería lm del R para regresión lineal simple
Este paquete ya está incluida al cargar el R.
Ejemplo 2
Tomemos el ejemplo del pollo.
Según su diagrama de dispersión, podría haber cierto grado de correlación, estimemos sus estadísticas:
La función que permite realizar un análisis de regresión es lm(…).
La relación entre las variables explicada y explicativa se establece usando el símbolo "~".
Veamos ls función lm(…) en su versión más simple:
>lm(prPollo~canPollo)
Resultados más detallados se obtiene anteponiendo:
>reg = lm(prPollo~canPollo)
Ahora procedemos a obtener un resumen de los estadísticos de regresión.
>summary(reg)
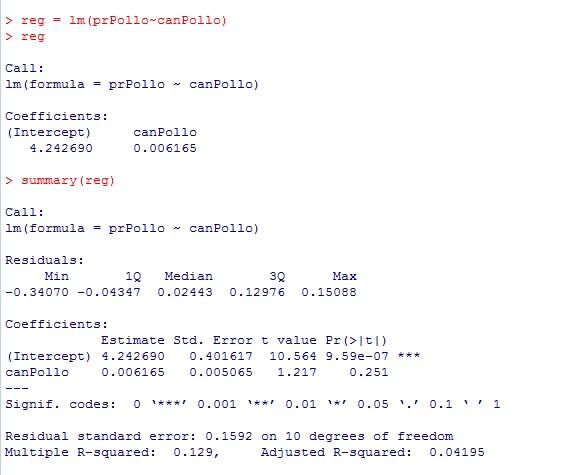
Otra forma de ingresar las dos variables es mediante el uso de data.frame, definida antes
> df=data.frame(prPollo,canPollo)
Su diagrama:
> etiq=c("Precio","Demanda")
y luego
>pairs(df,labels=etiq)
Y ahora
>lm(df)
Ejemplo 3
Cargar el paquete “xlsx”
library(xlsx)
Leer los datos del archivo agri.xlsx
> datos=read.xlsx("c:\\datosr\\agri.xlsx",1)
Nota
Si no estuviera el archivo, usamos agri.txt
> na = c("ProdAgr","FitoSanit","MaqAgr","Financ")
> datos=read.table("d:\\rpage\\agric.txt",col.names=na)
Visualizar los datos
>datos
Veamos diagramas de dispersión de estas variables
>pairs(datos[1:4])
Si incluimos una variable cualitativa, no se traza ningún diagrama con ella
> pairs(datos[1:5],col=c(3,2,4,5))
Haremos un attach para independizar las variables del data.frame
>d1 = attach(datos)
Obtendremos la matriz de varianzas y covarianzas:
>cov(d1)
La matriz de correlaciones. Se debe obtener desde el data.frame:
>cor(datos)
Ajustemos las variables ProdAgr(dependiente) y FitoSanit(independiente).
>reg1=lm(datos$ProdAgr~datos$FitSanit)
O usando las variables pues ya la desligamos de datos:
>reg1 = lm(ProdAgr~FitSanit)
Veamos lo que se ha obtenido:
>reg1
Nos muestra la relación de las variables y los coficientes de a y b, estimados.
Ahora un resumen completo del ajuste
>summary(reg1)
Ahora veamos el gráfico del ajuste
> plot(FitSanit,ProdAgr, xlab="Volumen de fitosanitarios",ylab="Volumen anual de producción")
La recta ajustada
>abline(reg1)
Cálculo de la tabla del ANOVA
>anova(reg1)
Intervalos de confianza para los parámetros a y b:
>confint(reg1,level=0.975)
El nivel de confianza se puede cambiar
Para la prueba de homocedasticidad y linealidad usaremos los residuales y los valores ajustados
>resid=rstandard(reg1)
>ajust=fitted(reg1)
Ahora los ploteamos para ver su comportamiento
>plot(resid, ajust)
Existe cierto grado de homocedasticidad, así como linealidad
En cuanto a la normalidad. Usaremos las funciones de gráfica de residuales
>qqnorm(resid)
>qqline(resid)
Ejemplo 4
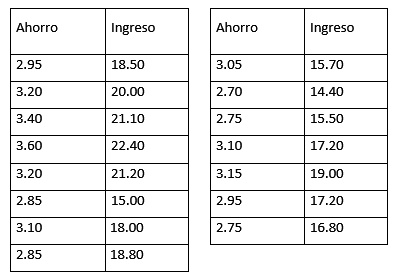
Vida S.A. es una empresa constructora de viviendas para el sector medio en Lima Metropolitana. Uno de sus nuevos proyectos consiste en construir viviendas para los trabajadores del sector público financiado por el sector Vivienda. Para ver la factibilidad del proyecto, Vida decide llevar a cabo un muestreo por conglomerados tomando en cuenta 10 entidades del sector público. De esta forma, eligió una entidad y de todos los empleados clasificados como de sector medio se tomó una muestra y se obtuvo de ella sus ingresos mensuales y su capacidad de ahorro, en miles de dólares. Estos datos se muestran en la siguiente tabla:

Se pide calcular
a) Construya un diagrama de dispersión. Interprete
b) Ajuste el modelo de regresión lineal simple. Interprete
c) Construya un gráfico de la línea de ajuste
d) Obtenga la tabla del ANOVA
e) Interprete el coeficiente de determinación
f) Obtenga e interprete el coeficiente de correlación
g) Obtenga el intervalo de confianza del 95% para el coeficiente de regresión
Solución
Definamos los objetos:
>Ahorro=scan()
>Ingreso = scan()
a) Diagrama de dispersión
>pairs(Ahorro~Ingreso)
b) >reg=lm(Ahorro~Ingreso)
>summary(reg)
c) El gráfico
>plot(Ingreso,Ahorro,xlab="Ingreso promedio mensual",ylab="Capacidad de ahorro mensual")
>abline(reg)
d) La tabla del ANOVA
>anova(reg)
e) >anova(reg)
Si Ho: los Ahorros y los Ingresos son independientes, entonces, según pValue y Fc, rechazamos esta hipótesis.
f) Del resumen de la regresión R² = 0.7185. Los datos indican que, el 71.86% de las veces, la variación de los Ahorros, están medianamente explicados por la variación de los Ingresos.
g) Puesto que el coeficiente de correlación es la raíz cuadrada de R², por lo que r = 0.7486. En el 84.76% de las veces, los Ahorros dependen de los Ingresos.
h) El intervalo de confianza del 95% para el coeficiente de regresión:
>confint(reg,level=0.95)

Por cada un mil soles que se incrementa los Ingresos, los Ahorros se incrementarán entre 55 y 121 soles.
Vamos a grabar los datos en el archivo ahorro.txt
Para ello, definamos un data.frame (lo veremos a continuación) llamado ingre
>ingre=data.frame(Ahorro, Ingreso)
>write.table(ingre,"c:\\datosr\\ahorro.txt",col.names=TRUE,sep=",")
Ejemplo 5
El archivo “grasas.txt”, contiene una muestra de tamaño 25, que contiene la edad, peso y la cantidad de grasa en la sangre. Cargue a R el archivo y realice un análisis lineal completo para presentar un informe detallado.
Solución
De la carpeta adecuada, cargamos los datos hacia la variable gr:
> gr=read.table("f:\\tempo1\\grasas.txt",header=T,sep=",")
Visualicemos los datos
>gr
Nombres de las variables
Esta tabla tiene una estructura de un dataframe (forma de una hoja de cálculo).
>names(gr)
¿Existirá alguna relación entre ellas?
Para ello debemos realizar un análisis de dispersión por pares:
>plot(gr) o >pairs(gr)
Un gráfico de cajas nos indica que la variable peso presenta un dato atípico
>boxplot(gr)
Podemos apreciar que sólo tiene sentido en realizar un análisis de regresión lineal entre Edad y Grasa. Para reforzar nuestra sospecha, veamos la matriz de correlaciones
>cor(gr)
La relación entre la Edad y la Grasa es directa, según el gráfico. Cuantitativamente,
>cov(gr)
Siendo positiva la covarianza entre estas variables, concluimos que la relación es directa, a mayor edad, mayor grasa. Apreciamos también que la grasa presenta mayor dispersión que la edad y el peso.
En consecuencia, nuestro modelo de estudio es:
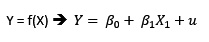
Donde Y será la variable explicada y X la regresora o explicativa.
Apliquemos el método de los MCO (Mínimo Cuadrado Ordinario) y dejaremos los resultados de la estimación en el objeto regl.
> regl=lm(grasas~edad, data=gr)
>summary(regl)
El modelo estimado es Y = 102.5751 + 5.3207 X + e
Con “e” los residuos de la estimación definido como e = Y – Yest, son independientes con distribución normal y varianza constante 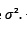
Si la edad se incrementa en un año, la cantidad de grasa en la sangre se incrementa en 5.3207 unidade de medida, con un 83.74% de grado de dependencia entre las dos variables, mientras que el 70.12% de la variabilidad del contenido de grasa en la sangre está explicada por la edad. El 29.88% de dicha variabilidad se debe a otros factores no considerados en el modelo, porcentaje que se encuentra explicado por la variable residual, e.
Veamos la recta de estimación en el gráfico de dispersión de los datos:
> plot(gr$edad,gr$grasas, xlab="Edad", ylab="Grasa")
> abline(regl)
Análisis inferencial del modelo
Veamos la tabla del Anova para comprobar la hipótesis de independencia de las dos variables:
>anova(regl)
Siendo el pValue menor que el 5% de signidicación, podemos afirmar que las dos variables están correlacionadas.
Volvamos a visualizar el resumen del modelo
>summary(regl)
En cuanto a los coeficientes de regresión del modelo, apreciamos que hay una columna donde se encuentra la desviación estándar de ambos estimadores, así como el t calculado y el pValue de ambos.
En el caso de la variable independiente Edad:
Su valor estimado: 5.3207, su error estándar: 0.7243, el tc = 7.346 y su pValue = 0. En consecuencia, se rechaza la hipótesis nula 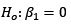 .
.
Veamos los intervalos de confianza para los coeficientes de regresión:
>confint(regl)
Si variamos el nivel de confianza al 90%,
>confint(regl, level=0.90)
Predicción:
¿Cuál será la cantidad de grasa en la sangre para una persona de 72 años?
En este caso: x0=70. Para ingresar al modelo debemos prepararlo como un dataframe:
> x0=data.frame(edad=72)
Estimemos Y0:
>Y0 = predict(regl,x0)
Si deseamos realizar un análisis predictivo para varios valores de x0, entonces:
> x0=data.frame(edad=seq(50,75,2))
El estimado 12 corresponde a una Edad = 72.
> Y0 = predict(regl,x0)
En cuanto a los intervalos confidenciales para la predicción:
Vamos a obtener los intervalos confidenciales para la media de Y, icm y para la Y predicha, icp, con un 95% de confianza:
Generamos un vector de valores x0:
> x0=data.frame(edad=seq(20,60))
Ploteamos el gráfico de dispersión y le añadimos la recta estimada
> plot(gr$edad,gr$grasas, xlab="Edad", ylab="Grasa")
>abline(regl)
Intervalo de confianza para la Y media (icm):
> icm=predict(regl,x0,interval="confidence")
En este caso, icm es una matriz de 3 columnas: la primera contiene los valores de la predicción, la segunda y tercera los extremos del intervalo de la predicción.
Trazamos las líneas de los extremos del intervalo (lty permite niveles de trazado)
> lines(x0$edad, icm[, 2], lty = 2)
> lines(x0$edad, icm[, 3], lty = 2)
Intervalo de confianza para la Y predicha (icp):
> icp = predict(regl, x0, interval = 'prediction')
> lines(x0$edad, icp[, 2], lty = 2,col="red")
> lines(x0$edad, icp[, 3], lty = 2,col="red")
Diagnóstico del modelo:
Cálculo de los valores de yest y los residuales:
>resid = rstandard(regl)
> yest=fitted(regl)
Su gráfico de dispersión:
>plot(resid,yest)
Este gráfico nos dice que las variables no tienen ninguna relación; es decir, son independientes
>cor(resid,yest) = -9.487366e-05
Esto indica que la hmosedasticidad y la linealidad son supuestos razonables.
Finalmente, comprobaremos el supuesto de normalidad de los residuales:
>qqnorm(resid)
>qqline(resid)
Confirma los supuestos.
Continuaremos en la siguiente sesión