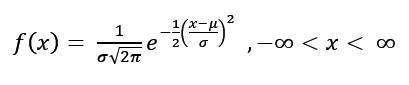
Usamos una nueva página, para desarrollar en exclusividad esta distribución normal, por su importancia en la Estadística y en todos los fenómenos de la actividad humana cuyo comportamieto sea capaz de ser medido usando cualquiera de las escalas de medición. Si una población, cuyas características se miden con una variable aleatoria X, su comportamiento se define por su función de distribución p(x) = P(X = x) cuando es una población discreta (Binomial, Poisson, Hipergeométrica, Geométrica, otras)  o f(x) cuando la población es continua (Uniforme, Exponencial, Normal, Chi Cuadrado, t, F, otras).. Pero cuando el tamaño de muestra es "suficientemente grande", la estadística nos provee de la fundamenación teórica para afirmar que el comportamiento de dicha población puede ser analizada bajo la distribución Normal, con media μ y varianza σ².

Si X -->N(μ,σ²),
La función de densidad de probabilidad de X, con media μ y varianza σ² se define como

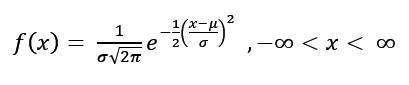
Un caso particular es la distribución normal estándar N(0,1) donde la media μ = 0 y varianza σ² = 1

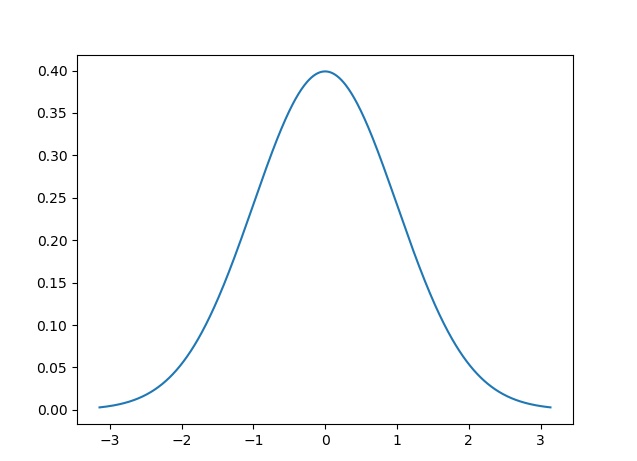
Una tabla de la distribución N(0,1) se muestra en la siguiente imagen

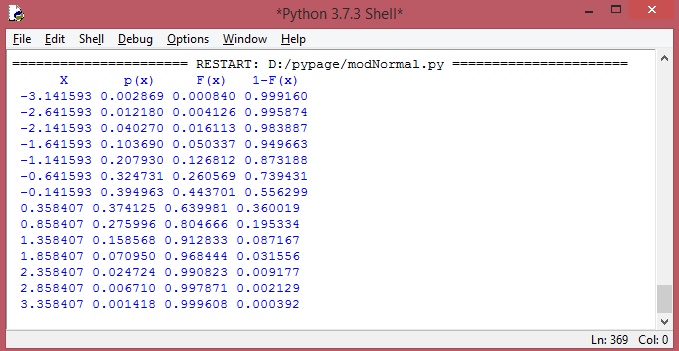
Del mismo modo, las gráficas de la función de densidad normal y su acumulada, para una N(0,1),se presentan en la siguiente imagen

Problema 1

En una compañía distribuidora de productos químicos, se observa que, el número de cajas de cierto medicamento, que se distribuye mensualmente a un establecimiento, es una variable aleatoria normal X, con una media de 257 cajas y una desviación estándar de 20 cajas.

a) ¿Cuál es la probabilidad de que en un establecimiento la compañia distribuya más de 280 cajas de ese tipo de medicamento?
b) ¿Cuál es la probabilidad de que, de 10 establecimientos por lo menos en 4 de ellos, la compañía distribuya más de 280 cajas?

Solución

Sea X: Nro de cajas distrbuidas en un establecimiento
X --> N(μ = 257, σ² = 60²)
El modelo para cálculo es

>>>Mn = st.norm(257,60)

a) Sea px = P(X > 280)
     px = 1-Mn.cdf(280)
     Resultado:
     0.350736

b) Si definimos a Y como el Número de establecimientos en los que la compañía distribuyó más de 280 cajas, entonces Y -->B(10, p), donde p = P(X > 280) = 0.350736

    Luego,
    >>> Mb = st.binom(10,0.350736)
    Si py es la probabilidad de que sean 4 por lo menos que reciban más de 280, tendremos
    >>> py = 1-Mb.cdf(4)
    0.2501




Continuar en la siguiente sesión