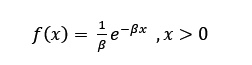
Su función de densidad es
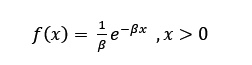
La variable aleatoria X -->Exp(β) se define cuando x > 0.
Y es decreciente siendo asintótica con el eje X
donde β es el parámetro de la distribución.
La función exponencial tiene una estrecha relación con la distribución de Poisson. Si μp es el promedio de personas atendidas por un cajero automático cada 30 minutos, μe es el tiempo promedio de atención por persona en dicho cajero automático.
Siendo u = μe el promedio de la distribución exponencial, entonces β = 1/μ = 1/u es el parámetro de la distribución.
En consecuencia, el modelo se obtiene con
Me = st.expon(β)
Veamos un caso:
Si en promedio 20 vehículos pasan por una caseta de control, cada 5 minutos, un vehículo pasará cada 5/20 = 0.25 minutos. En consecuencia, μp = 20 y μe = 0.25. Luego β = 1/0.25 = 4. Sea beta = 4
En consecuencia, el modelo para evaluación la conseguimos con
>>>Me = st.expon(beta)
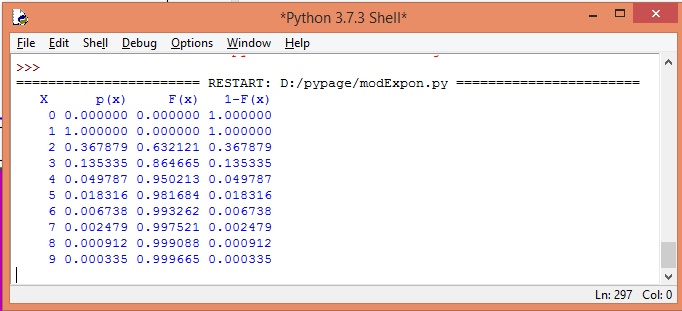
La tabla de la distribución de probabilidad, para algunos valores de x>0, se muestra en la siguiente tabla.
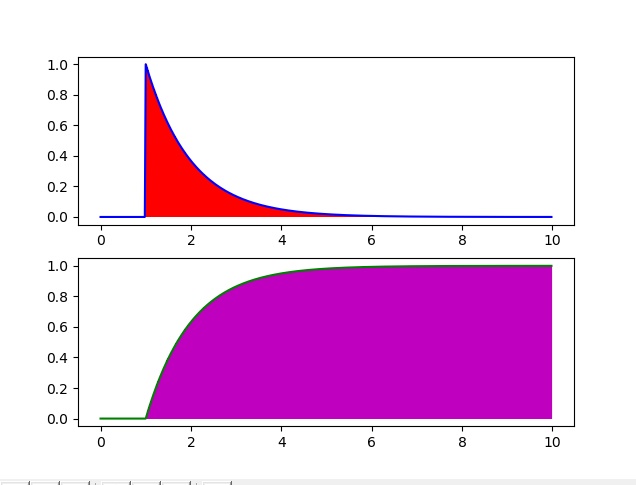
Por otro lado, las gráficas de la función de densidad y la función acumulada se muestran en la siguiente imagen.