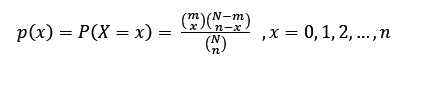
Distribución Hipergeométrica
Supongamos que, de un lote de 25 productos, 8 de los cuales son de procedencia extranjera, se selecciona una muestra de tamaño 5. Se desea saber la probabilidad de que en la muestra haya más de 2 productos extranjeros.
Sea X la variable definida comoel "Número de productos extranjeros seleccionados en la muestra".
Esta variable tiene distribución ipergeométrica de parámetros: N =25, m = 8, n = 5; ssiendo m los extranjeros y n el tamaño de la muestra.
El modelo hipergeométrico será X --> H(25, 5, 8); es decir,
El modelo es
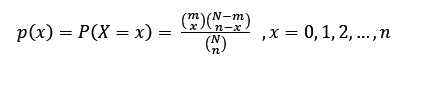
El modelo que nos permita evaluar será
>>>Mh = st.hypergeom(N,n,m)
La tabla de la distribución de probabilidad será
print(" X p(x) F(x) 1-F(x)")
for x in range(n):
print(" {0:4d} {1:6f} {2:6f} {3:6f}".format(x,Mh.pmf(x),Mh.cdf(x),Mh.sf(x)))
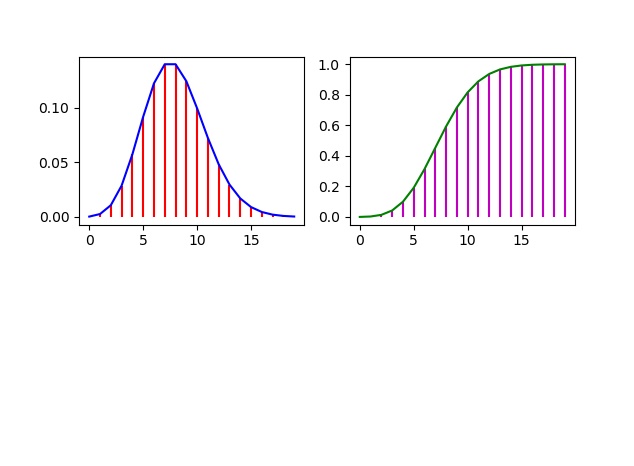
Sus gráficas
x = np.arange(5)
plt.subplot(211)
plt.plot(x,Mh.pmf(x),"b")
plt.vlines(x,0,Mh.pmf(x),"r")
plt.subplot(212)
plt.plot(x,Mh.cdf(x),"g")
plt.vlines(x,0,Mh.cdf(x),"m")
plt.show()
La tabla de la distribución de probabilidad y la probabilidad pedida será
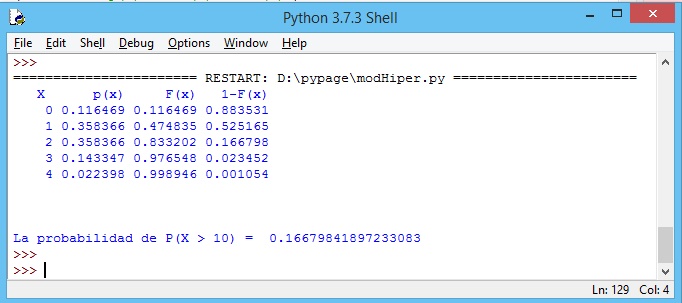
En cuanto a sus gráficas:
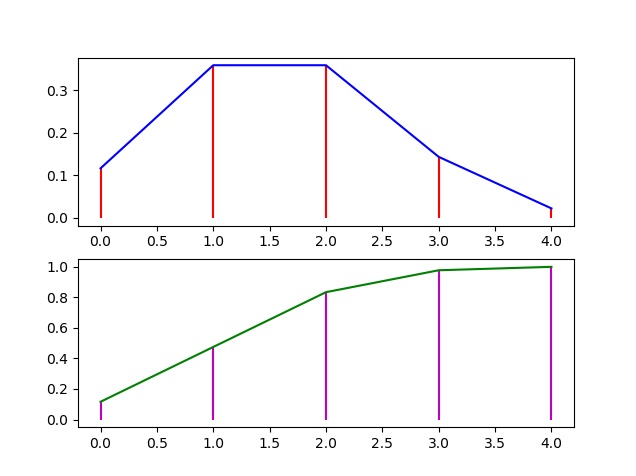
La probabilidd pedida: P(X>2) = 1 - P(X<=2) = 1 - F(2) = 1 - Mh.cdf(2)
>>>pr = 1 - Mh.cdf(2)
>>>pr
0.16679841897233083
Distribución Geométrica
El modelo geométrico consiste en realizar un experimento hasta que ocurra éxito por primera vez, en cuyo caso, el experimento se detiene. Para ello se define la variable X: Número de veces que debe repetirse el experimento hasta encontrar éxito por primera vez. Si la probabilidad de que en un juego de cartas, la probabilidad de que gane el juego es 0.2, ¿Cuál será la probbilidad de que gane a lo más en 3 intentos?
X --> G(p), donde p se define como la probabilidad de éxito.
La siguiente gráfica nos muestra el modelo
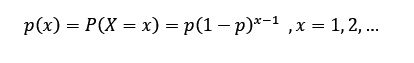
El modelo que nos permita evaluar la probabilidad de ocurrencias es
>>>Mg = st.geom(p)
Sea px = P(X <= 3), la probabilidad de ganar a lo más en 3 inentos. Entonces
px = Mg.cdf(3)
La tabla de distribución de probabilidad de X es
print(" X p(x) F(x) 1-F(x)")
for x in range(20):
print(" {0:4d} {1:6f} {2:6f} {3:6f}".format(x,Mg.pmf(x),Mg.cdf(x),Mg.sf(x)))
La imagen muestra la tabla
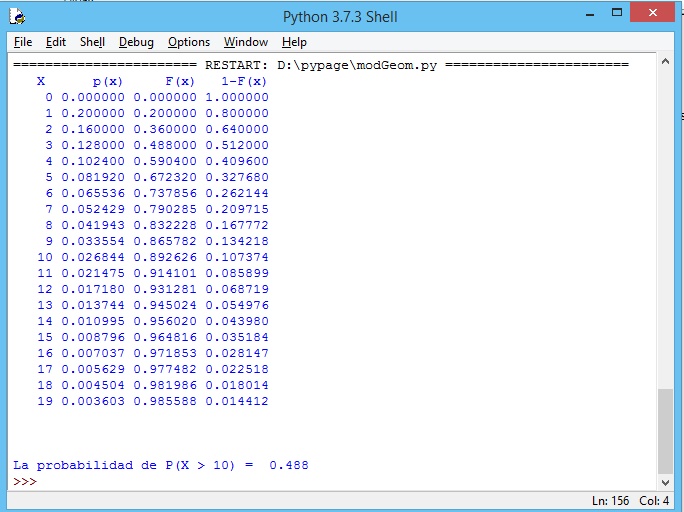
La gráfica de la misma es
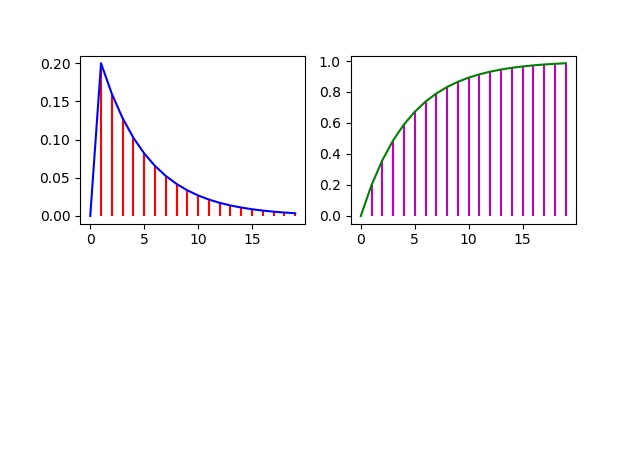
Distribución de Poisson
Esta variable se define como el número de veces que ocurre éxito dentro de un contexto. El contexto puede ser intervalo de tiempo, superficie, volumen, etc.
Por ejemplo: El número de errores tipográficos en por página de un libro; El número de llamadas que ingresa a una centralita elefónica cada 5 minutos; Número de clietes atendidos por un cajero automático por hora; etc. En todos ellos se presenta el parámetro o promedio de ocurrencias, λ.
El modelo viene dado por la siguiente imagen
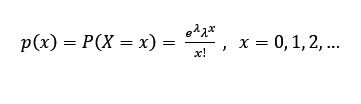
Supongamos que se define a X como el número de llamadas que una persona recibe por hora y que en promedio recibe 4 por hora, ¿cuál es la probabilidad de que en 2 horas reciba más de 10 llamadas?
El modelo para el cálculo de probabilidades, con m = 8 es la media o promedio de vehículos que llegan cada 2 horas, es
>>>m = 8
>>>Mp = st.poisson(m)
Como en las distribuciones anteriores, pasamos a generar la función de probabilidad o distribución de probabilidad, la acumulada y la inversa a la acumulada.
La tabla de la distribución de probabilidades y la probabilidad pedida, es
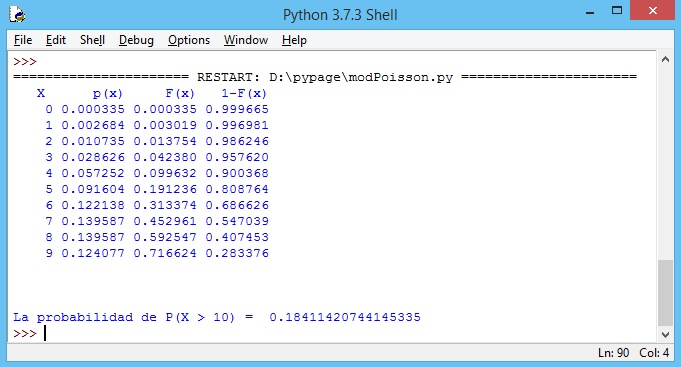
Finalmente las gráficas se muestran en la siguiente imagen