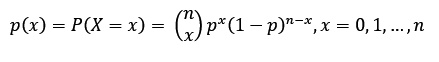
Cuando, estadísticamente hablamos de población, nos estamos refiriendo a todos los items, individuos o elementos que conforman el universo de un determinado fenómenos. Los ingresos de los trabajdores del secor salud, la oferta o demanda del pollo en el disrito de San Juan de Lurigancho, las facturas no pagadas de una entidad bancaria, las notas de los 120 alumnos de Estadística de la faultad de Economía de la Universidad TutanKamon, etc.
Cuando estas poblaciones presentan comportamientos no adecuados, es necesario analizar dicho comportamiento. Las manifestaciones del comportamiento, caracerística o propiedad constituyen los datos y, puesto que éstos varían de uno a otro elemento, se hace necesario mediante una variable.
Puesto que dichas manifestaciones pre determinadas no es sujeto de análisis pues estando determinadas se corrigen sin problema, la estadística se ocupa de aquellas no determinadas. Esto es lo que genera la aleatoriedad de sus manifestaciones, por lo que dichas variables poblacionales son variables aleatorias en su comportamiento.
Sin embargo, puesto que el análisis de una de las caracterísicas en cuestión implica analizar toda la población, lo cual no es práctico, se toma una parte de ella que sea representativa, a la cual se le llama muestra
Los datos que contituyen esta muestra no constituyen variables aleatorias pues están determinadas, ya no cambian; se hizo un corte a la población y la muestra es una fotografía de ella. Por lo que, las variables que puedan usarse en la muestra, representan a los diversos valores de esos datos que ya ocurrieron.
Ahora bien, el comportamiento de una variable aleaoria se define a través de sus parámetros. Del mismo modo, siendo la muestra una representación de la población, sus variables también la interpretan y su comportamiento se define por las estadísticas de la muestra
Demás de los parámetros que definen el comportamiento de una población y los estadísticos que definen el comportamiento de la muestra, tenemos las distribuciones de las variables aleatorias poblacionales y las Distribucione muestrales.
Mediante los parámetros podemos esperar que en un nuevo instante del tiempo la población se comporte de una forma determinada. Mediante los estadísticos de la muestra, podemos estimar o inferir esos parámetros para determinar el comportamiento de la población.
Puesto que al predecir estimar o inferir el valor de parámetro estamos corriendo un riesgo éste se evalúa mediante la>teoría de probabilidades.
Finalmente, las variables aleatorias que recoen el comportamiento poblacional, se expresan mediante las Distribuciones de probabilidad de las variables aleatorias. Del mismo modo, en la muestra, sin tener que ser probabilístico, siendo una muestra aleatoria la que mejor representa a la población, se usan las Distribuciones muestrales para inferir ocurrencias en la población.
Dicho esto, nuestro siguiente tema es
Ejemplos de fenómeno y variable aleatoria:
- Lanzar al aire una moneda y observar el número de caras otenidas
- Registrar el número de vehículos que pasa por una caseta de peaje, cada 30 minutos
- El peso de los pollos en una muestra de 30 pollos - El ingreso medio de los trabajadores mineros de la compañía Tia Bamba.
- Registrar el número de focos defectuosos en un lote de 25 focos, sabiendo que la probabilidad de encontrar un defectuoso es de 0.2
- El porcentaje de empleados con ingresos por debajo 1200 soles
- Registrar el número de focos defectuosos encontrados en una muestra de 5, de un lote de 100 focos, 10 de los cuales son defectuosos.
- La vaca es gorda
- Registrar el tiempo de espera de un vehículo en una caseta de peaje si se sabe que pasan por ella 40 cada media hora
- Los ingresos de los trabajadores del sector salud con una media de 2450 soles y una desviación de 60 soles
- etc.
Sin duda no son variables aleatorias los ejemplos: 3, 4 y 8. La 3ra es un dato; la 4ta es un estadístico y la 8va. no es variable.
Puesto que estas variables representan el comportamiento poblacional y éste se mide por su distribución de probabilidad,
- La 1ra tiene Distribución Binomial
- La 2da tiene Distribución de Poisson
- La 5ta tiene Distribución Binomial
- La 6ta tiene Distribución Binomial
- La 7ma tiene Distribución Hipergeométrica
- La 9na tiene Distribución Exponencial
- La 10ma tiene Distribución Normal
Para desarrollar las distribuciones de probabilidad usaremos las funciones de la librería scipy.stats
>>>import scipy.stats as st
>>>import numpy as np
Tambien debemos importar la librería de matplotlib,pyplo si deseamos graficar
>>>import matplotlib.pyplot as pt
Distribución Binomial
Su función de probabilidad
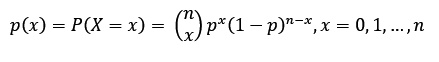
Supongamos que una persona 10 productos perecibles en una bodega. Según datos históricos se supone que el 10% de los productos es defectuoso.
En este caso, el número de ensayos es n = 10, la probabilidad de éxito (de encontrar un defectuoso) es p = 0.01
Si de finimos a la variable aleatoria X: Número de productos defectuosos adquiridos. Entonces X: 0, 1, 2, ..., 10
El modelo binomial viene dado por binom(n,p)
Mb = st.binom(n,p)
La función de probabilidad, px, se obtiene con pmf(x) La función de distribución acumulada F(x) = P(X <= x), se obtiene con cdf(x)
La probabilidad P(X > x) = 1 - F(x) = 1 - P(X <= x), se obtiene con sf(x)
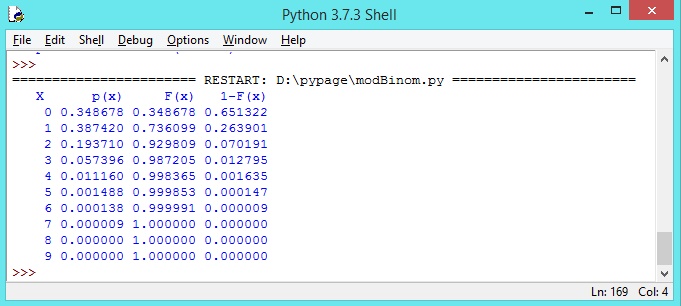
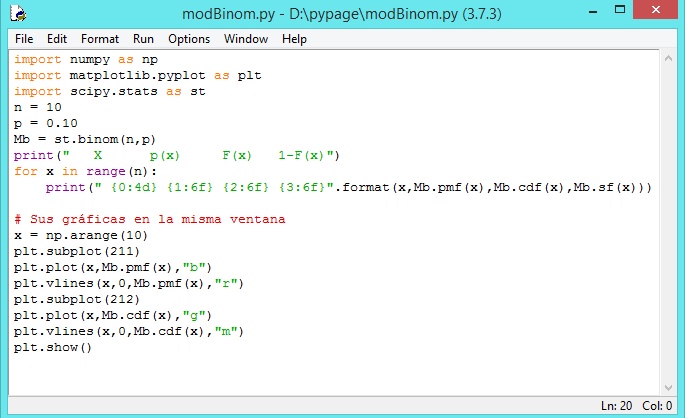
Creamos el modelo en un nuevo archivo de scripts llamado modBin.py
>>>Mb = st.binom(n,p)
Mediante un for, vamos a presentar la tabla de distribución para X
>>> print(" X p(x) F(x) 1-F(x)")
>>> for x in range(n):
print(" {0:4d} {1:6f} {2:6f} {3:6f}".format(i,Mb.pmf(x),Mb.cdf(x),Mb.sf(x)))
La tabla se encuentra en la siguiente imagen
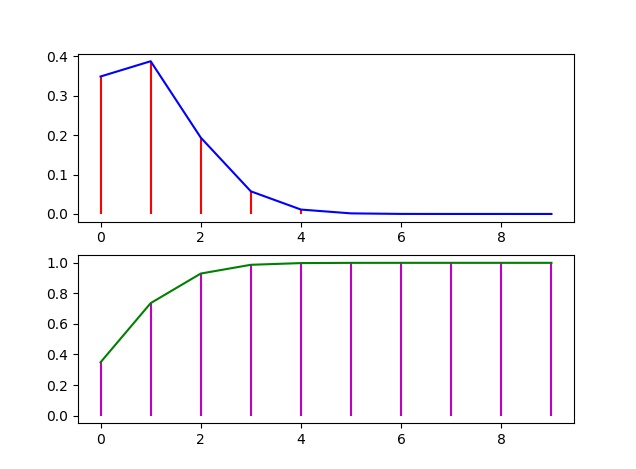
Vamos a graficar las dos distribuciones
Primero generamos un vector de los valores de 0 a 10 (según nuestro ejemplo)
>>>x = np.arange(n)
Queremos que las dos gráficas estén en la misma ventana
>>>plt.subplot(211)
Ploteamos la función de probabilidad
>>>plt.plot(x,Mb.pmf(x),"b")
Trazamos líneas verticales
>>>plt.vlines(x,0,Mb.pmf(x),"r")
Pasamos a la distribución acumulada
>>>plt.subplot(212)
>>>plt.plot(x,Mb.cdf(x),"g")
>>>plt.vlines(x,0,Mb.cdf(x),"m")
Ahora las mostramos
>>>plt.sow()
Una copia del archivo se muestra en la siguiente imagen
En la siguiente imagen se muestra las dos gráficas