En esta sesión, dejando para más adelante el uso de módulos, vamos a desarrollar un ejemplo de operaciones matriciales mediante el uso de funciones.

El objetivo es, definir una o dos matrices en la forma de listas numéricas en la consola y luego invocar a la función que fuera necearia y que estuviera definida.

Las funciones que vamos a desarrollar son:
- smat(A, B): Que se ocupará de la suma de matrices
- rmat(A, B): Que restará la matriz B de la matriz A
- prmat(A, B): Que nos permitirá obtener el producto de las dos matrices
- mulmat(A; B): Que nos devlverá la multiplicación matricial, con A(n,m) y B(m,p)
- mdet(A): Que nos devolverá la determinante de una matriz cuadrada
- minv(A): Que nos devolverá la inversa de la matriz A
- impre(A, msg): Que nos permitirá imprimir una matriz usando a msg como el título del reporte.

Para ello vamos a abrir un nuevo file para grabar con el nombre opmat.py

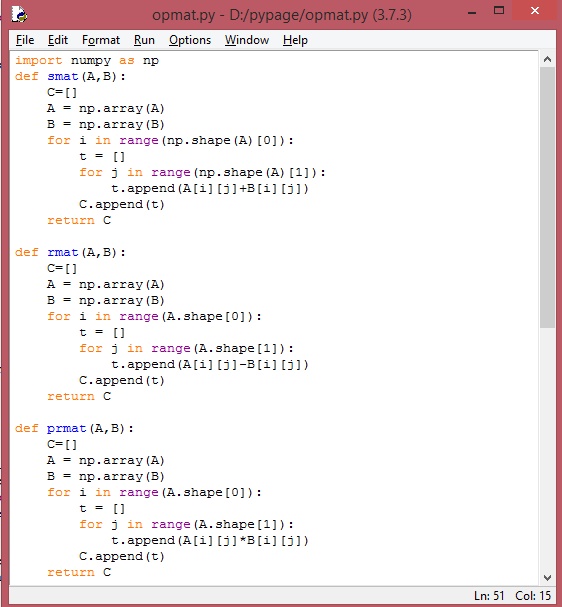
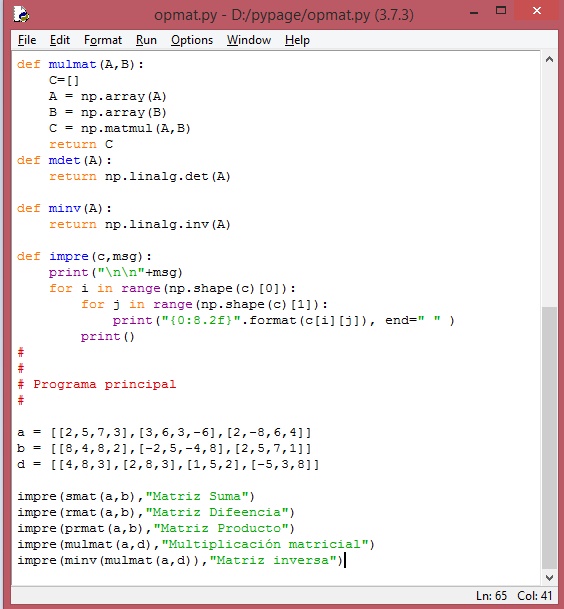
El siguiente es el código:

import numpy as np
def smat(A,B):
    C=[]
    A = np.array(A)
    B = np.array(B)
    for i in range(np.shape(A)[0]):
        t = []
        for j in range(np.shape(A)[1]):
            t.append(A[i][j]+B[i][j])
        C.append(t)
    return C

def rmat(A,B):
    C=[]
    A = np.array(A)
    B = np.array(B)
    for i in range(A.shape[0]):
        t = []
        for j in range(A.shape[1]):
            t.append(A[i][j]-B[i][j])
        C.append(t)
    return C

def prmat(A,B):
    C=[]
    A = np.array(A)
    B = np.array(B)
    for i in range(A.shape[0]):
        t = []
        for j in range(A.shape[1]):
            t.append(A[i][j]*B[i][j])
        C.append(t)
    return C
def mulmat(A,B):
    C=[]
    A = np.array(A)
    B = np.array(B)
    C = np.matmul(A,B)
    return C
def mdet(A):
    return np.linalg.det(A)

def minv(A):
    return np.linalg.inv(A)

def impre(c,msg):
    print("\n\n"+msg)
    for i in range(np.shape(c)[0]):
        for j in range(np.shape(c)[1]):
            print("{0:8.2f}".format(c[i][j]), end=" " )
        print()
#
#
# Programa principal
#

a = [[2,5,7,3],[3,6,3,-6],[2,-8,6,4]]
b = [[8,4,8,2],[-2,5,-4,8],[2,5,7,1]]
d = [[4,8,3],[2,8,3],[1,5,2],[-5,3,8]]

impre(smat(a,b),"Matriz Suma")
impre(rmat(a,b),"Matriz Difeencia")
impre(prmat(a,b),"Matriz Producto")
impre(mulmat(a,d),"Multiplicación matricial")
impre(minv(mulmat(a,d)),"Matriz inversa")

Ingrese este código y grabe con el nombre arriba indicado

Luego ejecute usando [Run] - [Run module]

En la consola obtendrá los resultados

Tenga presente que, para multiplicar dosmatrices, el orden de las dos matrices deben estar adeccuadmente definidas; es decir, tener a(n,m) y b(m, r) para obtener una matriz resultante c(n,r).
Igualmente, para invertir una matriz, debe definirse la matriz cuadrada; es decir, debe ser a(n,n).

Las imágenes siguientes nos muestran el código. Recuerde que la indentación es fundamental en el código.

Observe que antes de invocar a las funciones, se debe tener las matrices en forma de lista de listas. Al ser invocada una función, ésta convierte a la lista enviada, en arreglo, como se puede ver.



Continuar en la siguiente sesión