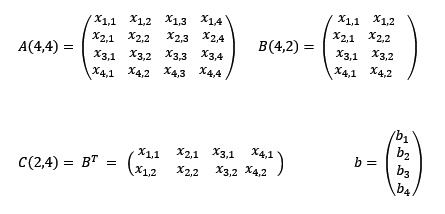
Un vector es una matriz, aunque un tipo especial de matriz, llamado arreglos unidimensionales. Sea vector fila A(i) de dimensión n o vector A(i) constituyen arreglos.
Un arreglo es realmente una matriz, cuando está compuesto por dos o más dimensiones y se denota por A(i,j) de n filas y m columnas, siendo su orden nxm. Dado dos o más vectores, podemos definir una matriz con ellos.
Una matriz tiene la forma
La siguiente imagen nos muestra la matriz A, de orden nxn; B, de orden nxm. También apreciamos la matriz C = BT que es la matriz transpuesta de B.
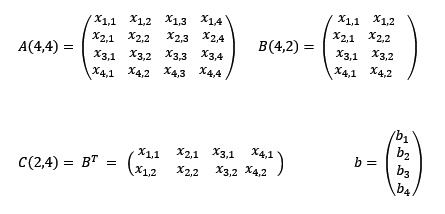
>Para trabajar con matrice se requiere de la librería numpy
>>>import numpy as np
Como ejemplos definmos algunas formas de definir una matriz de orden 2x2
- Primera forma:
>>>a = np.array([[5,3],[2,8]])
>>>a
- Segunda forma:
>>>b=[[1,8],[6,4]]
>>>b=np.array(b)
>>>b
Tercera forma:
>>> c1 = [3,-4,8,2]
>>> c2 = [6,4,0,1]
>>> c3 = [3,2,6,8]
>>>c = np.array([c1,c2,c3])
>>>c
Una matriz de orden 3x5 de zeros
>>>ceros = np.zeros((3,5))
Una matriz de unos, de orden 3x3
>>>unos = np.ones((3,3))
Operaciones matriciales
Ejemplo 1
Trabajemos con las matrices a y b
En c dejamos la suma de a y b
>>>c = a+b
En d, la diferencia
>>>d = a-b
En e la operación e = 5*a +8*b+c
>>>e = 5*a +8*b+c
>>>e
En f dejemos la multiplicación de a y b; es decir f = aij x bij
>>> f = a*b
>>>f
En g la multiplicación matricial de a y b
>>>g = a@b
>>>g En t la transpuesta de a
>>>t = np.transpose(a)
>>>t En ia la matriz inverza de a
>>>ia = np.linalg.inv(a)
>>>ia
array([[ 0.23529412, -0.08823529],
[-0.05882353, 0.14705882]])
Para comprobar que ia es la inversa de , multiplicamos ia por a
>>>ia@a
Ejemplo 2
Usemos la matriz c, definida líneas arriba
>>>c=np.array([c1,c2,c3])
Su orden es
>>>c.shape
(3, 4)
Ahora definamos la matriz d a partir de las listas d1, d2 y d3 que se definen como
>>> d1 = [3,8,1,2]
>>> d2 = [-3,-5,0,0]
>>> d3 = [8,6,7,2]
Ahora la matriz d tal que
>>>d = np.array([d1,d2,d3])
Su orden es
>>>d.shape
(3, 4)
Teniendo el mismo orden las dos matrices, podemos sumar, restar, multiplicar elemento por elemento pero no se puede realizar la multiplicación matricial. Para que se dé la multiplicación matricial de c por d, el número de columnas de c, debe ser igual al número de filas de d. Y esto no se da
En efecto:
>>>c@d
Traceback (most recent call last):
File "
c@d
ValueError: shapes (3,4) and (3,4) not aligned: 4 (dim 1) != 3 (dim 0)
Si transponemos d, tendríamos una matriz de orden (4, 3). En este caso sí podemos realizar la operación matricial
>>>td = np.transpose(d)
>>>td
En Efecto
>>>prod = =c@td
>>>prod
array([[-11, 11, 60],
[ 52, -38, 74],
[ 47, -19, 94]])
Ahora trabajemos con las matrices X, de orden 10x3 y el vector b, de orden 10x1
Sea X la matriz
>>>X = np.array( [
[52.95,71.66,85.58,63.69,72.81,68.44,52.46,70.77,82.03,74.39],
[386,446,512,401,457,458,301,484,517,503],
[40,38,53,42,49,47,35,48,53,47]])
El vector b
>>>b = np.array([6968,6055.68,8993.04,6142.08,8122.24,8659.28,3190.6,9644.16,10010.64,9655.68])
Con la propiedad np.shape, podemos verificar el orden de las matrices
>>>X.shape
(3, 10)
>>>b.shape
(10,)
En consecuencia, multipliquemos X por b para obtener un arreglo de orden (3,); es decir, un vector de 3 elementos
>>>prod = X@b
array([ 5537095.3984 , 35796157.72000001, 3607381.8 ])
En las siguientes sesiones dos aplicaciones de arreglos: Sistemas de ecuaciones y Regresión lineal .