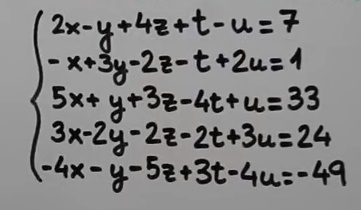
Ejemplo 3: Solición a los sistemas de ecuaciones lineles
Dado el sistema de ecuaciones lineales:
a11x1 + a12x2 + a13x3 ... + a1nxn = b1
a21x1 + a22x2 + a23x3 ... + a2nxn = b2
a31x1 + a32x2 + a33x3 ... + a3nxn = b3
...
an1x1 + an2x2 + an3xn3 ... + annxn = bn
Donde A es la matriz de coeficientes y b es el vector de términos independientes.
Supondremos que este sistema tiene solución.
Según esto, la solución para el vector x = (x1,x2, ... xn), será
x = A-1(ATbT), puesto que b es un vector fila.
Tomemos como primer ejemplo el siguiente sistema de ecuciones lineales:
3x + 6y - 5z = 0
x + y + 2z = 9
2x + 4y - 3z = 1
Vamos a encontrar la solución para x, y y z
Sea a la matriz de coeficientes y b el vector de términos independientes.
La matriz a es de orden (3x3) y b, de orden (1x3)
Definamos ambos objetos:
>>> a = np.array([[3,6,-5],[1,1,2],[2,4,-3]])
>>> b = np.array([[0,9,1]])
Transponemos la matriz a
>>> ta = np.transpose(a)
Sea A el producto de la transpuesa de a por a
>>>A = ta@a
En iA dejaremos la inversa de la matriz A
>>> iA = np.linalg.inv(A)
La solución la dejamos en el objeto o vector x:
>>>x = iA@(ta@bt)
>>>x
array([[1.],
[2.],
[3.]])
Es decir,
x<sub>1</sub> = 1
x<sub>1</sub> = 2
x<sub>1</sub> = 3
Ejemplo 2
La imagen siguiente nos muestra el sistemas de ecuaciones que queremos resolver:<br>
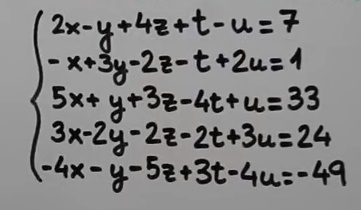
y el vector independiente
>>>a=np.array([[2,-1,4,1,-1],[-1,3,-2,-1,2],[5,1,3,-4,1],[3,-2,-2,-2,3],[-4,-1,-5,3,-4]])
Sea x el vector solución
>>>b = np.array([[7,1,33,24,-49]])
Obtenemos la matriz transpuesta
>>>ta = np.transpose(a)
>>>ta
Ahora, la transpuesta del vector b
>>>tb = np.transpose(b)
>>>tb
Calculemos todo a la vez
>>>x = np.linalg.inv(ta@a))@ta@tb
La slución es
>>>x