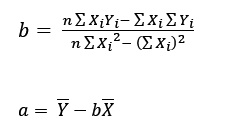
Ejemplo 2: Estimación lineal
En esta ocasión trabajando con dos vectores, vamos a realizar el proceso de estimar los coeficientes de regresión lineal simple de dos variables.
Esto es:
Dado el modelo Y = A + BX, vamos a utilizar el método de los Mínimos Cuadrados Ordinarios para estimar los valores de A y B a fin de realizar posteriormente, trabajos de inferencia estadística como las predicciones o proyecciones.
El modelo consiste en:
Dado Yi = A + BXi, diremos que b es el estimador de B, si
La siguiente imagen nos muestra cómo debemos calcular a y b que son los estimadores de A y B.
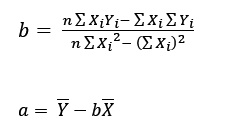
Procedimiento:
Cargamos a memoria numpy y pandas
>>>import numpy as np
>>>import pandas as pd
Leemos los datos del archivo ahorro.txt de la unidad "D" y la carpeta "pypage".
Como los datos no tienen cabecera, incluiremos los nombre en la lectura
>>>datos = pd.read_csv("d:\\pypage\\ahorro.txt",names=["Ahorro","Ingreso"])
>>>datos
Este es el data.frame que almacena las variables Ahorro e Ingreso.
Vamos a extraer los datos hacia dos variable Y y X
Esto lo hacemos con el pandas, usando la siguiente instrucción:
>>>X = datos.Ahorro
>>>Y = datos.Ingreso
>>>X
>>>Y
Esto lo podemos hacer gracias a que la lectura de dato con pandas no devuelve un data.frame de dos culmnas y 15 filas.
Calculamos el tamaño de la muestra, n, como usando len(X)
>>>n = len(X)
Cálculo de b:
>>>b=(n*sXY-sX*sY)/(n*sX2-sX**2)
Cálculo de a:
>>>a = sY/n-b*sX/n
Ahora la impresión de la ecuación estimada::
print("La ecuación de regresión estimada es: \n\nY = ",a,"+",b,"X")
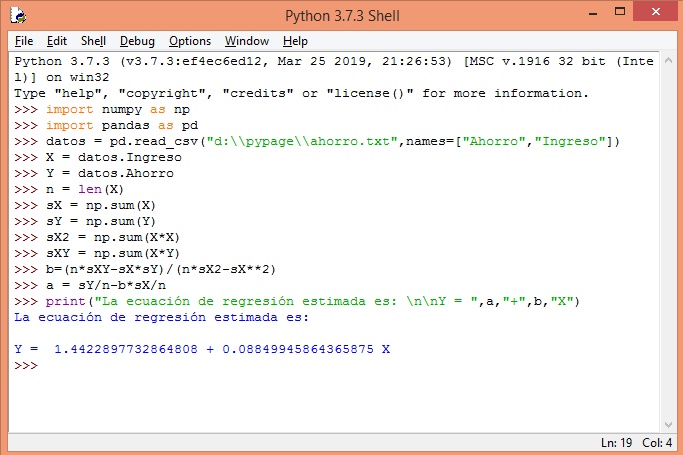
La siguiente imagen contiene el procedimiento
Ejemplo 3
Enunciado del problema:
Una empresa que vende por correo suministros para computadoras personales, software y hardware posee un almacén central para la distribución de los productos ordenados. Actualmente, la administración se encuentra examinando el proceso de distribución desde el almacén y está interesada en estudiar los factores que afectan los costos de distribución del almacén. Para dicho propósito se ha seleccionado una muestra de 24 meses y se han obtenido, los costos de distribución del almacén (en miles de dólares), las ventas (miles de dólares) y el número de pedidos recibidos. Los resultados de la encuesta se encuentran en el archivo "CostoVenta.xlsx", en la unidad D y carpeta "pypage". ¿Cuáles de las variables están relacionadas?.
Solución
Para saber si las variables está relacionadas e necesario calcular la covaianza entre las variables. También ayudará encontrar el Coeficiente de correlación entre las variables.
Lectura del archivo:
>>>datos = pd.read_excel("d:\\pypage\\CostoVenta.xlsx")
>>>datos
Las variables son:
Costo, Ventas, NroPed
Vamos a extraer las variables:
>>>Y = datos.Costo
>>>X = datos.Ventas
>>>Z = datos.NroPed
>>>n = len(X)
La siguiente imagen nos muestra la fórmula para calcular la "covarianza entre X e Y" y el "Coeficiente de correlación enre X e Y".
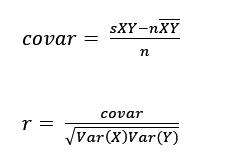
Procedimiento
Vamos a calcular las medias, varianzas de las tres variables, así como las covarianzas y coeficiente de correlación dos a dos.
>>>sX = sum(X)
>>>sY = sum(Y)
>>>sZ = sum(Z)
>>>sXY = sum(X*Y)
>>>sXZ = sum(X*Z)
>>>sYZ = sum(Y*Z)
>>>mY = np.mean(Y)
>>>mX = np.mean(X)
>>>mZ = np.mean(Z)
>>>vY = np.var(Y)
>>>vX = np.var(X)
>>>vZ = np.var(Z)
Las covarianzas entre ellos
>>>covXY = (sXY-n*mX*mY)/n
>>>covXZ = (sXZ-n*mX*mZ)/n
>>>covYZ = (sYZ-n*mY*mZ)/n
>>>rXY = covXY/np.sqrt(vX*vY)
>>>rXZ = covXZ/np.sqrt(vX*vZ)
>>>rYZ = covYZ/np.sqrt(vY*vZ)
Veamos los valores de los coeficientes de correlación:
>>>rXY
0.8421177731554735
>>>rXZ
0.8002768942405041
>>>rYZ
0.9188039900775353
Existe una buena relación entre las variables. Presentan un mínimo de 80% de dependencia.
Puesto que el coeficiente de correlación mide el grado (porcentual) de asociación entre las dos variables, podemos afirmar que Ventas y NroPed están fuertemente relacionadas; es decir, la dependencia entre ellas es mayor que entre las otras.