5.5 DISTRIBUCIÓN MUESTRAL DE LA DIFERENCIA DE
MEDIAS MUESTRALES
Sea X1, X2,…, Xn1
una muestra aleatoria extraída de una población
de parámetros μ1 y σ21.
Del mismo modo, sea Y1, Y2
,…, Yn2 una
muestra aleatoria extraída de una población de
parámetros μ2 y σ22.
Supongamos también que ambas poblaciones son independientes.
Sean  1 y
1 y  2
las medias de cada muestra con s21
y s22 las varianza de las
mismas.
2
las medias de cada muestra con s21
y s22 las varianza de las
mismas.
Diremos que  1
-
1
-  1
es una variable muestral llamada Diferencia muestral de medias, cuya
distribución de probabilidades viene dada por μ(
1
es una variable muestral llamada Diferencia muestral de medias, cuya
distribución de probabilidades viene dada por μ( 1
-
1
- 2) y
σ2(
2) y
σ2( 1
-
1
- 2).
2).
Donde
μ( 1
-
1
- 2) =
E(
2) =
E( 1 -
1 -  2 ) = E(
2 ) = E( 1 ) –E(
1 ) –E(  1 ) = μ1
- μ2 y
1 ) = μ1
- μ2 y
σ2( 1-
1- 2)
= V(
2)
= V( 1 ) + V(
1 ) + V( 2 )
2 )
El problema se presenta ahora en obtener V( 1
) y V(
1
) y V( 2 )
2 )
Así como al estudiar a  , la
media muestral de
medias, tuvimos que tomar en cuenta si la varianza poblacional era
conocida o no, así también debemos tomar en
cuenta si las varianzas poblacionales serán conocidas o no.
, la
media muestral de
medias, tuvimos que tomar en cuenta si la varianza poblacional era
conocida o no, así también debemos tomar en
cuenta si las varianzas poblacionales serán conocidas o no.
Caso 1: Cuando σ21
y σ22 son
conocidas
.
En este caso usaremos la distribución normal, por lo que

Caso 2: Cuando σ21
y σ22 son
desconocidas.
Siendo desconocidas las varianzas poblacionales, podría
ocurrir que sean iguales o diferentes. En ambos casos usaremos la
distribución t de Student para el cual supondremos
también que la población desde donde se extraen
ambas muestras son poblaciones normales.
Siendo desconocidas, supondremos que son iguales: σ21
= σ22

Siendo desconocidas, supondremos que son diferentes:
σ21
diferente a σ22

Ejemplo 14
Una muestra de tamaño 25 se toma de una población
normal con media de 80 y desviación estándar 5;
una segunda muestra de tamaño 36 se toma de una
población normal con media 75 y desviación
estándar de 3. Hallar la probabilidad de que la media de la
muestra de tamaño 25 exceda a la media de la muestra de
tamaño 36 en por lo menos 3.4 pero menos de 5.9.
Soluciónn
Según el problema:
n1 = 25; μ1 = 80;
σ1 = 5
n2 = 36; μ2 = 75;
σ2 = 3
Se pide P(3.4 ≤  1
-
1
- 2
<5.9)
2
<5.9)
Como las varianzas poblacionales son conocidas, usaremos la
distribución normal.
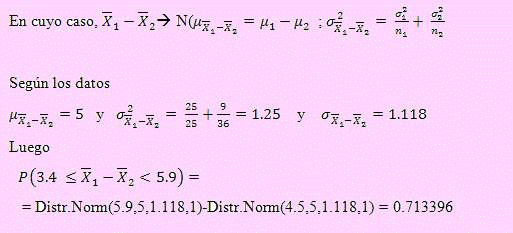
Ejemplo 15
Suponga que en el Ministerio de Trabajo se tiene registrado 20 mil
trabajadores de construcción civil (C) y 15 mil trabajadores
mineros (M).
El ingreso promedio mensual de los primeros es 900 soles
con desviación estándar de 300 soles mientras que
en el segundo, el ingreso promedio es de 1200 soles con un coeficiente
de variación de 15%. El gobierno otorga un aumento general
de 120 soles por costo de vida y 30 por movilidad.
Si luego del aumento
se realiza un muestreo de 45 trabajadores de construcción
civil y 64 mineros, ¿Cuál es la probabilidad de
observar una diferencia de a lo más 350 soles entre las
medias de ambas muestras?
Solución
La tabla siguiente muestra los datos del problema:

Ejemplo 16
Según los registros históricos de ONER las
bombillas fabricadas por la empresa PHIL, tiene una duración
media de 6000 horas, mientras que las bombillas fabricadas por la
empresa NATI tienen una duración de 8000 horas.
En una
investigación de control de calidad de bombillas se
encuentra que una muestra de 20 bombillas fabricadas por PHIL se
encontró una desviación estándar de la
vida útil de 1600 horas. Otra muestra aleatoria de 16
bombillas fabricada por la compañía NATI se
encontró que la desviación estándar de
la vida útil fue de 2600 horas.
¿Cuál
es la probabilidad de que el promedio de vida útil de las
bombillas fabricadas por NATI no difiera en más de 800 horas
del promedio de vida útil de las bombillas fabricadas por
PHIL?
Solución
El siguiente cuadro muestra los datos de este problema:

Pasamos a resolver la pregunta:
P( 1
-
1
- 2
≤ 800) = P(-800 ≤
2
≤ 800) = P(-800 ≤ 1
-
1
- 2
≤ 800)
2
≤ 800)
Siendo varianzas desconocidas usaremos t de Student con (n1 + n2 - 2)
grados de libertad. Esto significa que debemos realizar
transformación de variables.
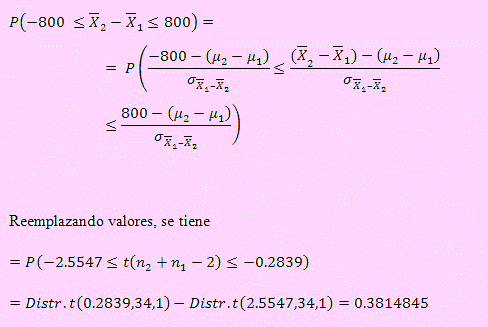
Ejemplo 17
El año 2011, una investigación tuvo por objetivo
analizar el comportamiento de los ingresos y gastos municipales de los
distritos de Lima Metropolitana. A falta de cifras completas, se
estudia una muestra de 11 distritos.
Los datos son los siguientes:
Para los ingresos:  1
= 0.60727272 s1 = 0.029014103
1
= 0.60727272 s1 = 0.029014103
Para los egresos:  2
= 0.55454545 , s2 = 0.04251203
2
= 0.55454545 , s2 = 0.04251203
a) Si se considera como logrado uno de los objetivos cuando:
“La
probabilidad de que en promedio los ingresos de todos los distritos de
Lima Metropolitana sean no menores a 0.58802 miles de millones de soles
fuera alta”.
Se considera que la probabilidad es alta cuando
esta sea mayor que 95%. ¿Puede afirmarse que se
logró la meta? Presente los supuestos empleados.
b) Calcular la probabilidad de que en promedio el ingreso de todos los
distritos de LM no exceda en más 0.095 miles de millones de
soles al nivel de egresos. Suponga que según cifras
anteriores, la heterogeneidad de los ingresos es similar a la de los
egresos de LM. Presente los supuestos empleados.
c) Calcular la probabilidad de que en promedio el ingreso de un grupo
de
11 distritos de LM no exceda en más de 0.0341 miles de
millones de soles al nivel de egresos. Suponga que según
cifras anteriores, la heterogeneidad de los ingresos es diferente a la
de los egresos de LM. Presente los supuestos empleados.
d) Cómo cambiaría su respuesta en las preguntas
a),
b) y c) si se sabe que por cifras anteriores, la variabilidad de los
ingresos debe ser de 0.0234 y la de los egresos 0.0456 miles de
millones de soles?
Solución
Según el problema las varianzas poblacionales no son
conocidas. De manera que, donde corresponda, usaremos la
distribución t de Student. Para ello recuerde que debemos
construir la variable
T=( -
μ)/(s ⁄ √n) → t(n-1).
-
μ)/(s ⁄ √n) → t(n-1).
Supondremos que la población de los ingresos y egresos de
todos los distritos de LM son normales e independientes.
a) De acuerdo a la pregunta, si P(μ ≥ 0. 0.58802)
>
0.95 se habrá logrado la meta.
Calculemos dicha probabilidad.

Como esta probabilidad es mayor al 95% entonces podemos afirmar que
sí se lograron los objetivos.
b) Por la forma cómo se plantea la pregunta, debemos hallar:
P(μ1 – μ2
≤ 0.095)
Como en el caso anterior, usaremos la distribución t de
Student.
Supuesto: Varianzas poblacionales desconocidas pero iguales
(según datos)
Según esto

d) Dejamos como ejercicio esta pregunta. Sólo se trata de
volver a calcular cambiando las desviaciones estándares.
Recuerde que:
Cuando se trate de diferencia de medias, ante todo ver si se conoce las
varianzas poblacionales.
Si son conocidas, usar la
distribución muestral. Si no fueran conocidas, usar la
distribución t de Student con varianzas iguales o diferentes.
5.6 DISTRIBUCIÓN MUESTRAL DE LA DIFERENCIA DE
PROPORCIONES MUESTRALES
Sea X1, X2,…, Xn1
una muestra aleatoria extraída de una población
Bernoulli. Del mismo modo sea Y1, Y2,…,
Yn2 una muestra aleatoria
extraída de una población Bernoulli.
Si definimos a X = ∑(Xi) y Y = ∑
(Yi como el número de
éxitos en la primera y segunda muestra, respectivamente,
entonces ambas variables tendrán distribución
Binomial de parámetros π1 y
π2.
Si definimos a
p1 = X/n1 como la
proporción muestral de éxitos
en la primera muestra y p2= Y/n2
como la proporción
muestral de éxitos en la segunda muestra, entonces diremos
que p1 - p2 es una
variable aleatoria muestral definida como la
diferencia de proporciones muestrales cuya distribución
muestral viene dada por su media y su varianza; es decir, por
μ(p1 - p2 ) y
σ2(p1
- p2) .

Ejemplo 18
Se cree que el 30% de las mujeres y el 20% de los hombres aceptan
cierto producto. Si se hace una encuesta a 200 hombres y 200 mujeres,
elegidos al azar, ¿cuál es la probabilidad de que
más mujeres que hombres acepten el producto?
Solución
Ante todo, formulemos las definiciones que sean necesarias y
extraigamos los datos del problema según estas definiciones:
Sea X: Número de mujeres que aceptan dicho producto.
π1: Proporción de mujeres que
aceptan dicho producto
Sea Y: Número de hombres que aceptan dicho producto.
π2: Proporción de hombres que
aceptan dicho producto
Según esto: π1 = 0.30, π2
= 0.20; n1 = 200 y
n2 = 200
Debemos calcular: P(X > Y)
Como no tenemos información sobre las distribuciones de X e
Y (aunque sí se sabe pues ellas tienen
distribución Binomial; pero debemos resolver el problema por
variables proporcionales) haremos la siguiente deducción:
P(X > Y)= P(X / n1 >Y / n2
)= P(p1 > p1 ) =
P(p1 - p2 > 0)
Como la distribución de p1 - p2
es N(π1 - π2
,(π1 (1 - π1))/n1
+ (π2 (1 - π2))/n2
); es
decir que p1 - p2
→ N(0.10,0.04311632)
Luego P(p1 - p2 >
0) = 1 - Distr.Norm(0,0.10,0.0431163,1)= 0.9898
Ejemplo 19
Los asesores de un candidato presidencial opinan que la
proporción de ciudadanos a favor de su líder es
de 52.5% en Lima Metropolitana y 50% en provincias. Si se seleccionan
muestras aleatorias de 400 y 250 en LM y provincias, respectivamente,
¿cuál es la probabilidad de que la
proporción muestral de LM supere a la proporción
muestral de provincias en más del 5%?.
Solución
π1: Proporción de ciudadanos a
favor de su
líder en LM
π2: Proporción de ciudadanos a
favor de su
líder en Provincias.
p1: Proporción de ciudadanos en la
muestra a favor de su
líder en LM
p2: Proporción de ciudadanos en la
muestra a favor de su
líder en Provincias.
Según el problema:
Π1 = 0.525; Π2
= 0.50; n1 = 400 y n2
= 250
Se pide que encontremos P(p1 - p1
> 0.05)
Para resolver por normal, necesitamos encontrar su media y su varianza.
μ(p1 - p2)
= 0.025 y σ2((1
- p2) = 0.040292
Luego
P(p1 - p2 > 0.05)
= 1-Distr.Norm(0.05,0.025,0.02029,1)= 1 - 0.732536 = 0.267464
Ejemplo 20
Se cree que, de cada 100 baterías producidas por SOURCE, 10
son defectuosas y de cada 100 baterías fabricadas por
FUENTE, 5 son defectuosas. Si se toma muestras al azar de 250
baterías tomadas de la producción de SOURCE y
otra de 300 unidades de las fabricadas por FUENTE,
¿cuál es la probabilidad de observar una
diferencia menor o igual a 0.02 en las proporciones muestrales de
baterías defectuosas?
Solución
Si definimos a
π1: Proporción de
baterías SOURCE
defectuosas, entonces π1 = 0.10
Y si π2: Proporción de
baterías FUENTE
defectuosas, entonces π2 = 0.05.
Debemos encontrar P( | p1 - p2
| ≤ 0.02)
P( | p1 - p2 | ≤
0.02) = P( 0.02 ≤ p1 - p1
≤ 0.02)
Ahora sólo falta encontrar la media y varianza de p1
- p2 .
Realizando los cálculos: μ(p1
- p1 ) = 0.05 y
σ2(p1
- p1 ) = 0.02766942
Con lo cual
P( 0.02 ≤ p1 - p2
≤ 0.02)
= Distr.Norm(0.02,0.05,0.02277,1) - Distr.Norm(-0.02,0.05,0.02277) =
0.09278
5.7 DISTRIBUCIÓN MUESTRAL DEL COCIENTE DE
VARIANZAS MUESTRALES
Sea X1, X2 , …
, Xn1 una muestra
aleatoria extraída de una población normal de
parámetros σ21.
br>
Del mismo modo, sea Y1, Y2,
… , Yn2 una
muestra aleatoria extraída de una población
normal de parámetros σ22.
Supondremos también que ambas poblaciones son independientes.

Nota 1:
Toda vez que se necesite resolver probabilidades de la forma P(s21
< s22) o algunas
de sus formas, deberemos realizar una transformación de
variables hasta conseguir la forma cómo se define a T para
luego utilizar la distribución F de Fisher a fin de
encontrar la probabilidad buscada.
Nota 2:
Si las varianzas poblacionales son iguales u homogéneas
entonces la variable muestral: cociente de varianzas muestrales debe
tomar la forma T=(s21 / s22
) para tener una
distribución F de Fisher con n 1 - 1
y n2 - 1 grados de libertad
en el denominador y denominador, respectivamente.
Ejemplo 21
Se tienen dos variables normales independientes, tales que:
a) Calcular , siendo: n1 = 12 y n2
= 15.
b) Hallar k tal que: , siendo: n1 = 24 y n2
= 20.
Solución

b) Dado P(s21 ≤ a22)
= 0.88, primero dividiremos entre s22
y luego debemos transformarla
en una variable que se distribuya como F(: n1 -
1, n2 - 1) y finalmente
lo igualamos a 0.88.
En efecto

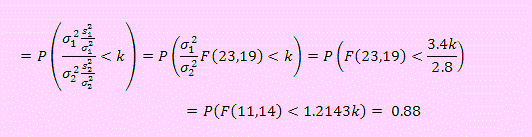
Puesto que no se conoce el valor para el cual se tiene P(F <
1.2143k) = 0.88,
Usando la función inversa en F obtenemos:
Distr.F.Inv(0.12,23,19) = 1.7074745
Esto significa que 1.7074745 = 1.2143k, de donde k = 1.40614
Ejemplo 22
Estudios anteriores plantearon que la heterogeneidad en el nivel
alcanzado por el PBI en América Latina, medida a
través de la variabilidad de esta variable al interior de la
región latinoamericana, siempre ha existido; esto es, de un
año a otro puede esperarse que exista una similar
variabilidad en el nivel del PBI registrado por los países
latinos.
Partiéndose del PBI, expresado en millones de
dólares, se obtuvieron los siguientes resultados: Que la
desviación estándar del PBI registrado para el
2003 en una muestra de 16 países latinos fue de 67,803
mientras que para 2004 fue de 95,136.09.
Cuál es la
probabilidad de que exista una mayor variabilidad en el año
2004 respecto a 203? Plantee los supuestos necesarios e interpreta los
resultados.
Solución
Supondremos que la población (niveles de PBI de
América Latina) desde donde se extrae la muestra durante los
años 2003 y 2004, son normales e independientes.
Supondremos también que las muestras tomadas son del mismo
tamaño e igual a 16
Sean s21 y s22
las varianzas muestrales de los años 2003 y 2004,
respectivamente. Sabemos que σ1 =
67803 y σ2 = 95136.09.
Debemos calcular P(s21
< s22 ). Para ello
debemos transformar el cociente en una variable F(n2
- 1, n1 - 1).
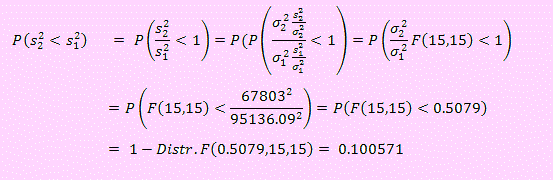
5.8 PROBLEMAS PROPUESTOS
1. La empresa Estilos SA se dedica a la venta de artículos
de
tocador. Sus ventas semanales alcanzan un promedio de 12500
dólares con una desviación de 5700
dólares. Si
estas ventas se registran durante 36 semanas,
¿Cuál
será la probabilidad de que el promedio de sus ventas por
semana
hayan alcanzado un máximo de 14000 dólares?
2. Suponga que en el problema anterior sólo se sabe que sus
ventas mensuales en promedio fueron de 12500 pero nada se sabe respecto
a la desviación estándar. En la muestra tomada en
cuenta
en las 36 semanas permitió calcular una
desviación
estándar de 4800 dólares. Cuál
será la
probabilidad de que la venta promedio por semana de la muestra sea
superior a 13000 dólares? Suponga que la
población desde
donde se extrajo la muestra es normal.
3. La duración en horas de una pila de reloj se distribuye
exponencialmente con una media igual a 1000 horas. Si se toma una
muestra de 100 pilas, ¿Cuál será la
probabilidad
de que la duración media de la muestra sea superior a 1100
horas?
4. Water SA. es una empresa que se encarga de envasar agua mineral en
botellas de 620 ml. El proceso tiene ciertas deficiencias pues sufre
una pérdida en su contenido medio que era de 5 ml por
botella
con una desviación estándar de 1.2 ml. Si para
comprobar
esto se realiza una muestra de 36 botellas y se acepta que el contenido
medio es de 5 ml siempre que el contenido medio en la muestra se
encuentre entre 4.5 y 5.5 ml; en caso contrario, se rechaza.
¿Cuál es la probabilidad de aceptar que la media
es de 5
ml si realmente el contenido medio es de 4.8 ml?
5. Se el error muestral ε la hemos definido como |  - μ |, en una muestra de tamaño 36, seleccionadas de
una
población normal cuya desviación
estándar es 324,
- μ |, en una muestra de tamaño 36, seleccionadas de
una
población normal cuya desviación
estándar es 324,
a) ¿Qué porcentaje tendrán un error
muestral mayor a 4.5?
b) ¿Para qué valor de K, el 95% tienen un error
muestral no mayor a K?
6. Un representante de ventas de una tienda selecciona una muestra de
36 clientes de un total de 400 que adquirieron un cupón por
la
compra en dicha tienda. El monto de los 400 clientes constituye una
población finita con una media de 2500 dólares y
una
desviación estándar de 660 dólares.
¿Cuál es la probabilidad de que la media de la
muestra
supere los 2765 dólares?
7. Durante un determinado proceso electoral en un cierto
país,
una encuestadora estima que el 40% de los electores están a
favor del candidato Pedro Bueno.
Si se selecciona una muestra aleatoria de 600 electores,
¿Cuál será la probabilidad de que la
proporción de electores a favor de Pedro Bueno
esté entre
37% y 45%?
Qué tamaño de muestra se debería
escoger si se
desea tener una probabilidad de 0.97 de que la proporción de
electores a favor de Pedro Bueno en la muestra no se diferencie en
más del 2% de la verdadera proporción de
electores a
favor de Pedro Bueno?
8. Un analista de mercado desea obtener una muestra suficientemente
grande de manera que la probabilidad de que la proporción
obtenida a favor de un cierto producto resulte inferior al 35% sea
igual a 0.0062. ¿Cuál es el tamaño de
la muestra
si se supone que la verdadera proporción a favor del
producto es
0.4
9. Para controlar la calidad en el llenado de latas de conservas de
anchoveta, se seleccionan aleatoriamente muestras de 46 latas
diariamente. Si la proporción de latas defectuosas en el
llenado
es al menos K, se detiene el proceso para su revisión; en
caso
contrario, se continúa con el llenado. Determine el valor de
K
de forma que la probabilidad de detener el proceso sea 0.9332, cuando
el proceso de llenado contenga el 8% de llenado defectuoso.
10. Para tener información respecto de la variabilidad en
las
notas obtenidas por un alumno se tomó una muestra de 20
alumnos
matriculados en una determinada asignatura. Si la muestra se extrajo de
una población normal cuya varianza de notas es de 16
puntos²,
¿Cuál será la
probabilidad de que la
varianza en dicha muestra sea superior a 15?
11. Se tomaron dos muestra aleatorias independientes de
tamaño
21 y 9, respectivamente, de una población de
baterías y
se registraron su vida útil. ¿Cuál es
la
probabilidad de que la varianza de la primera muestra sea superior al
doble de la varianza de la segunda muestra?
12. Una agencia distribuidora de café afirma que el peso
promedio de las bolsas de dos tipos de café que distribuye
es la
misma. Para probar esta afirmación se tomaron dos muestras
aleatorias de tamaño 36 de cada tipo de café.
Si el peso medio de la primera muestra es mayor al peso medio de la
segunda muestra, se aceptará que el peso medio de ambos
tipos de
café es la misma; en caso contrario, se rechazará
la
afirmación. Si las varianzas de los pesos de las bolsas son
de 9
y 4, respectivamente,
¿Cuál es la probabilidad de
aceptar
la afirmación?
13. Un sindicato de trabajadores de una empresa quiere presentar un
pliego de reclamos salariales el próximo mes. Para sustentar
su
reclamo y comparar el ingreso medio de los trabajadores de su empresa
con el de otra empresa, toma dos muestras independientes de 16 y 13
empleados, respectivamente, encontrando las desviaciones
estándares iguales a 120 y 55 dólares,
respectivamente.
¿Cuál es la probabilidad de que la diferencia
entre los
ingresos medios en las muestras no sea mayor que 65, si se sabe que los
ingresos medios en ambas empresas son iguales y dichos ingresos
provienen de poblaciones normales?. Qué supuestos usa para
resolver este problema?
14. El 30% de mujeres y el 20% de varones prefieren salir de paseo
familiar un fin de semana. Si se selecciona una muestra aleatoria de
200 mujeres y 200 hombres, ¿Cuál será
la
probabilidad de que la diferencia entre las proporciones de mujeres y
hombres que desean salir de paseo un fin de semana en la muestra,
esté en el intervalo (-0.19, 0.19)?
15. En una encuesta a boca de urna se selecciona a 600 electores que ya
votaron y se les pregunta por qué candidato votaron. Si en
las
últimas encuestas se sabía que el 30% de
electores
estaban a favor del candidato A y el 35% estaban a favor del candidato
B;
¿Cuál será la probabilidad de que
la
proporción de electores que votaron por B en la muestra
supere a
los que votaron por A en al menos 10%?
Siguiente sesión.
 1 y
1 y  2
las medias de cada muestra con s21
y s22 las varianza de las
mismas.
2
las medias de cada muestra con s21
y s22 las varianza de las
mismas.  1
-
1
-  1
es una variable muestral llamada Diferencia muestral de medias, cuya
distribución de probabilidades viene dada por μ(
1
es una variable muestral llamada Diferencia muestral de medias, cuya
distribución de probabilidades viene dada por μ( 1
-
1
- 2) y
σ2(
2) y
σ2( 1
-
1
- 2).
2). 1
-
1
- 2) =
E(
2) =
E( 1 -
1 -  2 ) = E(
2 ) = E( 1 ) –E(
1 ) –E(  1 ) = μ1
- μ2 y
1 ) = μ1
- μ2 y  1-
1- 2)
= V(
2)
= V( 1 ) + V(
1 ) + V( 2 )
2 ) 1
) y V(
1
) y V( 2 )
2 ) , la
media muestral de
medias, tuvimos que tomar en cuenta si la varianza poblacional era
conocida o no, así también debemos tomar en
cuenta si las varianzas poblacionales serán conocidas o no.
, la
media muestral de
medias, tuvimos que tomar en cuenta si la varianza poblacional era
conocida o no, así también debemos tomar en
cuenta si las varianzas poblacionales serán conocidas o no.


 1
-
1
- 2
<5.9)
2
<5.9)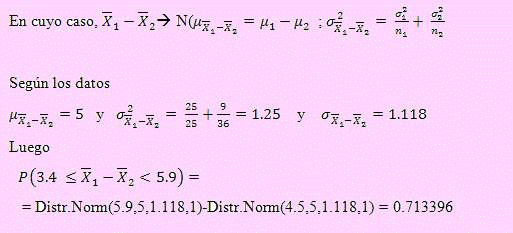


 1
-
1
- 2
≤ 800) = P(-800 ≤
2
≤ 800) = P(-800 ≤ 1
-
1
- 2
≤ 800)
2
≤ 800)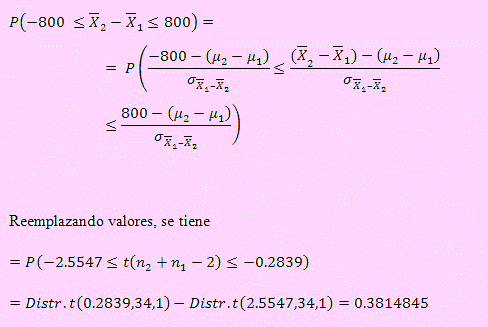
 1
= 0.60727272 s1 = 0.029014103
1
= 0.60727272 s1 = 0.029014103 2
= 0.55454545 , s2 = 0.04251203
2
= 0.55454545 , s2 = 0.04251203 -
μ)/(s ⁄ √n) → t(n-1).
-
μ)/(s ⁄ √n) → t(n-1).





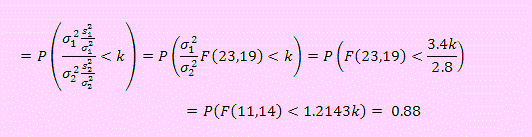
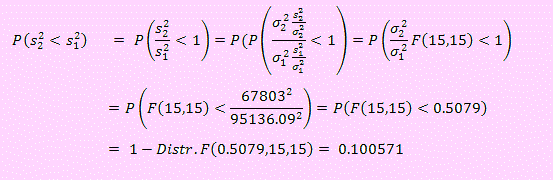
 - μ |, en una muestra de tamaño 36, seleccionadas de
una
población normal cuya desviación
estándar es 324,
- μ |, en una muestra de tamaño 36, seleccionadas de
una
población normal cuya desviación
estándar es 324,