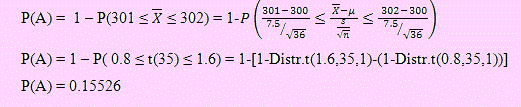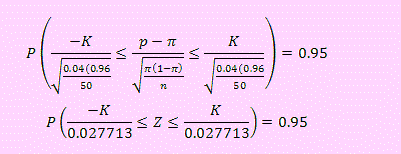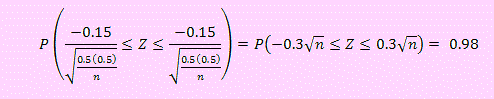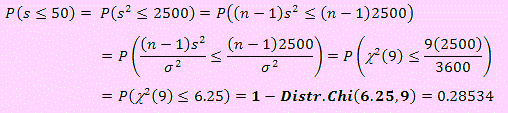CAPÍTULO 5
DISTRIBUCIONES MUESTRALES
5.1 Introducción
5.2 Distribución muestral de la media
5.3 Distribución muestral de la proporción
5.4 Distribución muestral dela varianza
5.5 Distribución muestral de la diferencia de medias
5.6 Distribución muestral de la diferencia de proporciones
5.7 Distribución muestral del cociente de varianzas
5.8 Problemas propuestos.
5.1 INTRODUCCIÓN
Empecemos este capítulo abriendo el archivo Distrib muestrales. Haga clic en el botón [Obtener estadísticas]. En este ejemplo se dispone de los ingresos mensuales de 1200 trabajadores de una determinada empresa. El objetivo del muestreo es estimar el ingreso mensual promedio así como la variabilidad de los mismos, a fin de comparar con los ingresos mensuales promedios de otros sectores. Para ello se han tomado muestras aleatorias de tamaño 38.
Como puede apreciar, se han extraído 5 muestras del mismo tamaño. Se ha calculado la media y la varianza de cada una de ellas. Se puede apreciar que las medias muestrales difieren una de otra en una cantidad muy pequeña. Para propósitos de esta introducción, supondremos que se puede obtener la media poblacional, en este caso es 2400.66.
Comparando cualquiera de las medias con el de la población se puede ver que cualquiera de ellas podría ser seleccionada como un representante de la media poblacional (que es desconocida). Del mismo modo también se ha obtenido la media de las medias muestrales, que se encuentra en la celda L41. Creemos que este indicador de la muestra puede ser el mejor representante de las cinco medias correspondientes a estas cinco muestras. Este nuevo promedio de promedios no es el resultado de un cálculo sobre los datos de la muestra. Por ello podemos considerarla como una nueva variable, pero en este caso en una muestra, a la cual podríamos llamarla media muestral.
Si hacemos lo mismo con las varianzas muestrales, podríamos crear otra variable muestral que la podríamos llamar varianza muestral.
Esto sugiere el estudio de nuevas variables llamadas variables muestrales. Cada una de ellas tendrá su media, su varianza, su propia distribución y por tanto podemos resolver problemas de probabilidad relativo a estas variables pues cada una de ellas constituye una variable aleatoria. En el presente capítulo nos ocuparemos del estudio de estas variables.
5.2 DISTRIBUCIÓN MUESTRAL DE LA MEDIA
Media muestral
Una muestra de tamaño n,extraída de una población cuya media es μ y varianza σ², constituida por un conjunto de variables aleatorias independientes X1, X2,…, Xn es una muestra aleatoria y los n valores que toma X serán los datos que conforman la muestra.
Tomando en cuenta lo dicho en la introducción, supongamos que se han extraído k muestras aleatorias de la población de tamaño N. Si  1,
1,  2 ,…,
2 ,…, k son las medias muestrales de cada una de las muestras, entonces podemos afirmar que
k son las medias muestrales de cada una de las muestras, entonces podemos afirmar que  , media aritmética de las medias muestrales, es una variable aleatoria definida como Media muestral.
, media aritmética de las medias muestrales, es una variable aleatoria definida como Media muestral.
Siendo  una variable aleatoria, entonces debe tener una distribución de probabilidad la cual estará definida por su media μ
una variable aleatoria, entonces debe tener una distribución de probabilidad la cual estará definida por su media μ y su varianza σ2
y su varianza σ2 , donde
, donde
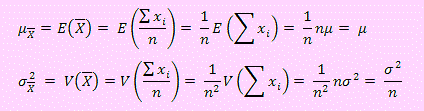
Nota 1
Siendo  una variable aleatoria y tiene una distribución de probabilidad, es natural preguntarnos: ¿Se puede calcular P(
una variable aleatoria y tiene una distribución de probabilidad, es natural preguntarnos: ¿Se puede calcular P( ≤ k)?
≤ k)?
El siguiente teorema nos autorizará el uso de la distribución normal para resolver problemas como se plantea en la pregunta, bajo ciertas condiciones.
Teorema del Límite central
Sea X1, X2, …, Xn una muestra aleatoria extraída de una población de parámetros μ y σ2. Si  es la media muestral, entonces Z= (
es la media muestral, entonces Z= ( - μ)/(σ/ √n) es una variable normal estándar, siempre que n sea suficientemente grande (n ≥ 30).
- μ)/(σ/ √n) es una variable normal estándar, siempre que n sea suficientemente grande (n ≥ 30).
Nota 2:
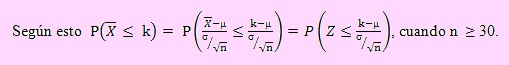
Cuando la varianza poblacional es conocida
La Distribución muestral de la media muestral ¯X, cuando la varianza poblacional σ^2 es conocida, aplicando el Teorema del Límite Central, será normal con μ  = μ y σ2
= μ y σ2 = σ2/n, según la deducción realizada líneas arriba. Luego
= σ2/n, según la deducción realizada líneas arriba. Luego  → N(μ , σ2/n).
→ N(μ , σ2/n).
Cuando la varianza poblacional es desconocida
Si la varianza poblacional es desconocida y la población desde donde se extrae la muestra es normal, entonces la variable T=( - μ )/(s/√n) → t(n-1). Esto es, cuando la varianza poblacional no sea conocida, usaremos la distribución t de Student para resolver el problema.
- μ )/(s/√n) → t(n-1). Esto es, cuando la varianza poblacional no sea conocida, usaremos la distribución t de Student para resolver el problema.
Ejemplo 01
Los ingresos mensuales que perciben los médicos de EsSalud, de una cierta área, se distribuyen normalmente con un ingreso medio de 3500 soles y desviación estándar de 700 soles.
a) Si el 18% de ellospagan impuestos, ¿cuál es el ingreso mensual mínimo de un médico de esta áreaque paga impuestos?
b) Si se escoge al azar una muestra de 150 médicos de dicha área y se registran sus ingresos, ¿cuál es la probabilidad de que el promedio de la muestra se diferencie de su valor real en no más de 100 soles?
Solución
Sea X la variable definida como “El ingreso mensual de un médico”
Según el problema: X → N(3500, 7002)
Esto es μ = 3500 y σ = 700
a) Sea K la cantidad mínima a partir de la cual se paga impuestos. Esto significa que un médico pagará impuestos si X ≥ K.
La probabilidad de que esto ocurra es P(X ≥ K ) = 1 – P(X < K) = 0.18.
Despejando P(X < K ) = 0.82
En Excel:
Luego P(X < K ) = Distr.Norm.Inv(0.82,3500,700) = 4140.76
b) En este caso n = 150.
La frase “El promedio de la muestra se diferencia de su valor real” se puede expresar simbólicamente como |  - μ | ≤ 100.
- μ | ≤ 100.
Usamos valor absoluto puesto que la diferencia puede ser positiva o negativa.
Luego
P(| - μ |≤100 )= P(μ -100 ≤
- μ |≤100 )= P(μ -100 ≤  ≤ μ + 100)=P(3400 ≤ μ ≤ 3600)= F(3600) – F(3400)
≤ μ + 100)=P(3400 ≤ μ ≤ 3600)= F(3600) – F(3400)
= Distr.Norm(3600,3500,700,1)-Distr.Norm(3400,3500,700,1)
= 0.5567985 – 0.4432015 = 0.113597
Nota 3:
Recuerde que, cuando se usa la función Distr.Norm, el último argumento debe ser 1 para que devuelva la probabilidad acumulada.
Ejemplo 02
MoviClaro afirma que el tiempo que emplean los clientes en pagar sus facturas es una variable normal de valor medio 30 días y desviación estándar 8 días.
a) Si se escogen al azar las cuentas de 40 clientes, ¿cuál es la probabilidad de observar un promedio muestral inferior a 32 días?
b) Si la muestra es de 25 cuentas, ¿qué tan probable es de tener un promedio entre 28.5 y 32.5 días?
c) En una muestra al azar de 16 cuentas, ¿qué valor máximo tomará el promedio con probabilidad 0.90?.
Solución
Sea X: Tiempo que un cliente se tarda en pagar sus facturas.
Según los datos: X → N(30, 64)
Donde es μ = 30 y σ = 8

Ejemplo 03
De un lote de focos ahorradores enviados por un proveedor, se han tomado al azar, 12 focos. El propósito es observar la duración del producto para determinar su conveniencia en compras futuras. Se les dejaron encendido hasta que se quemen. Los datos (en horas) obtenidos con el experimento fueron:
120, 128, 132, 130 124, 127, 130, 135, 122, 129, 131, 130.
Si el proveedor indica que su producto tiene una duración media de 127.5 horas.
a) Calcule la media de la muestra y luego determine la probabilidad de que una muestra del mismo tamaño arroje un promedio superior al que usted calculó.
b) ¿Cuál es la probabilidad de que la media muestral se aparte del valor real en a lo más 2 horas?
br> Solución
Ingrese los datos a una hoja en un nuevo libro o abra el archivo Prob01. Calculemos primero la media de la muestra; es decir,  .
.
Por lo que sabemos,  = (∑Xi / n = Promedio(B2:B13) = 128.167
= (∑Xi / n = Promedio(B2:B13) = 128.167
Por si fuera necesario, calculamos también la varianza y la desviación estándar
s² = Var(B2:B13) = 18.515 y s = DesvEst(B2:B13) = 4.303
a) Debemos calcular P(  > 128.167).
> 128.167).
Como la varianza poblacional no es conocida, usaremos la distribución t.
Para ello, debemos construir la variable T= ( - μ)/(s/√n) talque T → t(n-1)
- μ)/(s/√n) talque T → t(n-1)
Luego
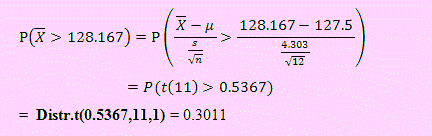
Nota importante
Recuerde que Distr.t(a, gl, 1) = P(X > a)
b) En este caso se pide P(|  – μ | ≤ 2).
– μ | ≤ 2).
Aplicando el valor absoluto
P(| – μ | ≤ 2) = P(-2 + 127.5 ≤
– μ | ≤ 2) = P(-2 + 127.5 ≤  ≤ 2 + 127.5 )=P( 125.5 ≤
≤ 2 + 127.5 )=P( 125.5 ≤  ≤ 129.5)
≤ 129.5)
Transformando  a una variable t(n-1), tenemos
a una variable t(n-1), tenemos
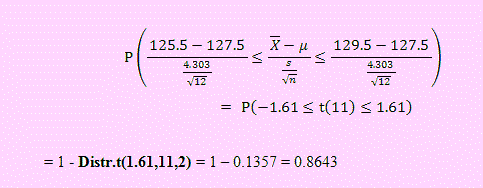
Ejemplo 04
Un exportador de espárragos envasa sus productos en frascos cuyo contenido medio es de 300 gramos. Para controlar el proceso automático de llenado, se selecciona cada hora una muestra de 36 frascos. Si el peso neto medio de la muestra está entre 301 y 302 gramos, el proceso continúa; en caso contrario, se detiene y se reajusta la máquina.
a) ¿Cuál es la probabilidad de detener el proceso que está operando con una desviación estándar de 7.5 gramos?
b) Si Ud. fuera el responsable del proceso, ¿deberá reajustar la máquina?
Solución
Sea X: El contenido de un frasco de espárragos (gramos).
Nótese que en cada hora se está tomando la muestra de tamaño n = 36.
Como el frasco contiene 300 gramos, supondremos que este indicador constituye el contenido medio. No se conoce la varianza.
a) El proceso continúa si 301 ≤  ≤ 302.
≤ 302.
Sea A: El evento definido como el proceso debe ser detenido.
Si la probabilidad de que el proceso continúe es P(301 ≤  ≤ 302)
≤ 302)
Entonces P(A) = 1 – P(301 ≤ ¯X ≤ 302).
Si  0 =301.5 y s = 7.5, usando la distribución t de Student tendremos:
0 =301.5 y s = 7.5, usando la distribución t de Student tendremos:
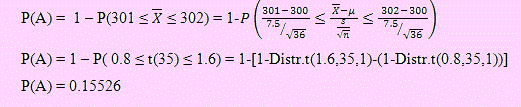
Creo que el proceso debe ser detenido para reajustar la máquina pues el porcentaje de veces que el contenido no está en el rango especificado es suficientemente considerable.
5.3 DISTRIBUCIÓN MUESTRAL DE LA PROPORCIÓN
Dada una población formada por elementos que poseen o no cierta característica, diremos que el indicador o parámetro π constituye la proporción de elementos que poseen dicha característica.
Si un experimento aleatorio tiene dos únicos resultados: éxito o fracaso y se ejecuta una sola vez, diremos que la población es de Bernoulli donde π representa la proporción de éxitos y 1 – π representa la proporción de fracasos. Si el experimento se repite n veces, podemos afirmar que la población es Binomial. Y cuando se realiza un muestreo con reposición, se dice que la población desde donde se extrae la muestra es una población Binomial.
Sea X1, X2,…, Xn una muestra aleatoria independiente extraída de una población de Bernoulli en donde si Xi = 1 ocurre éxito, si Xi = 0 ocurre fracaso.
Si ahora definimos a X= ∑(i=1)nXi, como el número de éxitos obtenidos en esta muestra, entonces X constituye una variable Binomial tal que su valor esperado es E(X) = μ = nπ y su varianza V(X) = σ² = n π(1- π).
Si definimos a p = X/n como la proporción de éxitos o la proporción, diremos que p es una variable muestral cuya distribución de probabilidad viene dada por μp y σ2p .

Ejemplo 05
El gerente de McAllum Inc. cree que el 30% de los pedidos a su empresa provienen de clientes nuevos. Para comprobar esta afirmación se toma una muestra aleatoria de 100 clientes que hicieron sus pedidos en la empresa.
a) Suponga que el presidente está en lo correcto y que π = 0.30. ¿Cuál es la distribución muestral de p para este estudio?
b) ¿Cuál es la probabilidad de que la proporción muestral esté a ± 0.05 o menos de la proporción poblacional?
Solución
Sea π la proporción de pedidos provenientes de clientes nuevos. Según el problema, π = 0.30. Igualmente n = 100.
a) Si definimos a p como la proporción muestral de pedidos provenientes de clientes nuevos, entonces la distribución muestral de p será p → N(π,π(1-π)/n); es decir, p → N(0.30,0.0021). En este caso σp = 0.04582576
b) Se pide encontrar P( | p – π | ≤ 0.05)
P( | p – π | ≤ 0.05) = P(0.25 ≤ p ≤ 0.35 )
= Dstr.Norm(0.35,0.3,0.04583) - Distr.Norm(0.25,0.3,0.04583)
= 0.724722
Ejemplo 06
Un mayorista compra vasos de vidrio en grandes cantidades directamente de la fábrica. Inspecciona una muestra al azar de 50 vasos de un lote recién adquirido para determinar la proporción de vasos rotos o defectuosos. Suponiendo que en realidad el lote ha sido enviado con 4% de vasos rotos o defectuosos.
a) ¿Cuál es la probabilidad de que la muestra contenga como máximo 3 vasos rotos?
b) ¿Qué diferencia máxima encontrará Ud. entre la proporción de la muestra y su valor real con probabilidad 0,95?
Solución
Sea X: El número de vasos rotos o defectuosos en el lote.
Sea π: La proporción de vasos rotos o defectuosos en el lote.
Según el problema π = 0.04
Tamaño de la muestra, n = 50.
a) Se pide P(X ≤ 3).
Se sabe que P(X ≤ 3) = P(X/50 ≤ 3/50)= P(p≤0.06)
Como p → N(0.04, 0.000768) en donde σp = 0.02771281
Entonces P(p ≤ 0.06) = F(0.06) = Distr.Norm(0.06,0.04,0.02771281) = 0.764757
Según el problema debemos hallar una diferencia máxima, digamos K tal que P(┤|p - π| ≤ K)=0.95
Aplicando valor absoluto tenemos: P(-K ≤ p – π ≤ K ) = 0.95
Para hallar K debemos estandarizar la variable muestral p. Para ello es suficiente dividirá toda la inecuación entre la desviación estándar de p; esto es,
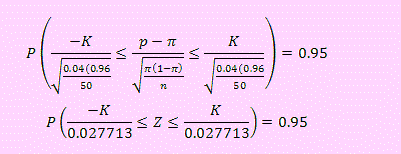
En la siguiente gráfica se muestra
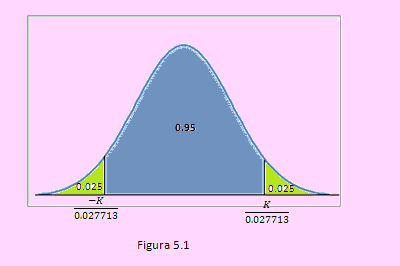
En este gráfico tenemos P(Z<(-K)/0.027713)=0.025
Usando inversa en N(0,1) hallaremos el valor del cociente; es decir,
(-K)/0.027713=Distr.Norm.inv(0.025,0,1)= -1.96
De donde K = 0.0542
La diferencia entre ellos es del 5.42%.
Ejemplo 07
El Jefe de Prácticas pre profesionales de una universidad afirma que el 60% de los egresados consigue empleo con una remuneración mensual mayor que US$ 500. Para comprobar esta afirmación se escoge una muestra aleatoria de 600 egresados de esa universidad. Si la proporción de egresados de los que consiguen trabajo con una remuneración mensual mayor que US$ 500 se encuentra entre 0.55 y 0.65, se aceptará la afirmación; en caso contrario se rechazará.
a) ¿Cuál será la probabilidad de rechazar la afirmación?
b) Si realmente el 70% de todos los egresados consiguen trabajo con una remuneración mensual mayor que US$ 500, ¿cuál será la probabilidad de aceptar la afirmación?
Solución
Sea π: la proporción de egresados que consiguen empleo con una remuneración superior a US$ 500. Según datos, π = 0.60
Tamaño de muestra = n = 600.
Sea p: la proporción de egresados en la muestra que consiguen empleo con una remuneración superior a US$ 500.
a) Se aceptará la afirmación si 0.55 ≤ p ≤ 0.65
Sea A el evento: Aceptar la afirmación y A’ el evento: Rechazar la afirmación.
Según esto
P(A’) = 1 – P(A) = 1 – P(0.55 ≤ p ≤ 0.65)
Como la distribución p es p → N(0.60, 0.6(0.4)/600) donde σp = 0.02, con lo cual P(A’) = 1–(Distr.Norm(0.65,0.6,0.02,1)–Distr.Norm(0.55,0.6,0.2,1)) = 0.98758
b) En este caso π = 0.70. Debemos hallar P(A). Como p → N(0.7,0.7(.3)/600) donde σp = 0.01871
Con lo cual
P(A) = Distr.Norm(0.65,0.7,0.01871,1)-Distr.Norm(0.55,0.7,0.01871)
P(A) = 0.003766
Ejemplo 08
El gerente financiero de una gran empresa comercial desea contar con información sobre la proporción de clientes a los que no les agrada su nueva política de gestión, respecto al tratamiento de los cheques girados con cantidades por debajo de $ 500.
¿Cuántos clientes tendrá que incluir en una muestra si desea que la proporción de la muestra se desvíe a lo más en 0.15 de la verdadera proporción, con una probabilidad de 0.98. Considere que para el gerente un cliente al que no le agrada la política implementada posee las mismas características que un cliente al que sí le agrada dichas políticas.
Solución
Según los datos: | p – π | ≤ 0.15 y según el problema, P(| p – π | ≤ 0.15) = 0.98
P(| p – π | ≤ 0.15) = P(-0.15 ≤ p – π ≤ 0.15)= 0.98.
Para encontrar el tamaño de la muestra debemos estandarizar, con lo cual,
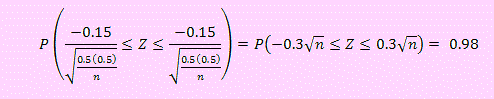
La gráfica nos índica lo que debemos hacer
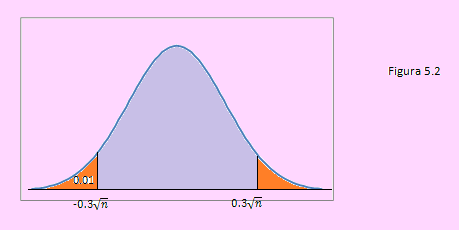
Según esto P(Z < -0.3√n )= 0.01
Como Distr.Norm.Inv(0.01,0.1) = -2.32635 entonces < -0.3√n = -2.32635
De donde n ≅ 60
5.4 DISTRIBUCIÓN MUESTRAL DE LA VARIANZA
Sea X1, X2,…, Xn una muestra aleatoria extraída de una población normal de parámetros μ y σ2.

Ejemplo 09
Los transistores fabricados por una compañía tienen una duración media de 2000 horas con una desviación típica de 60 horas. Si se selecciona una muestra de 10 transistores al azar de una población normal, ¿Cuál será la probabilidad que la desviación estándar muestral:
a) No supere las 50 horas?
b) Se encuentre entre 50 y 70 horas?.
Solución
Sea X: La duración de los transistores.
De acuerdo a los daos: X → N(2000, 3600)
n = 10
a) Se pide calcular P(s ≤ 50)
Puesto que la variable muestral es s² y no s y además debemos obtener la variable que tenga distribución Chi – cuadrado, de acuerdo a la última nota.
Por tanto
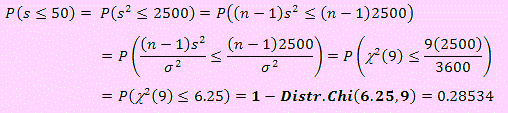
b) En este caso se pide calcular P(50 ≤ s ≤ 70) Usando el mismo procedimiento de transformación de variable empleado en a):

Ejemplo 10
En una determinada prueba se supone que las calificaciones se distribuyen normalmente con un promedio de 80 puntos y desviación estándar de 10 puntos. Si mañana se debe aplicar una prueba de aptitud a 12 aspirantes:
a) ¿Cuál sería la probabilidad de que la desviación estándar de las calificaciones se dichos aspirantes sea mayor que 15 puntos?
b) ¿Cuál debería ser el mínimo valor de la desviación estándar de las calificaciones de dichos aspirantes con una probabilidad de 0.95?
Solución
Primero extraeremos los datos:
Sea X: La calificación obtenida por un aspirante
Según el problema: X → N(80, 100)
n = 12; σ = 10
a) Se pide evaluar P(s > 15)
Transformando hacia una Chi-cuadrado, lo que está dentro de los paréntesis: P(s>15)= p(s2 > 225)=1-P(s2 ≤ 225)=1-P(χ2(11) ≤ (11(225))/100) = 0.0099
b) Supongamos que K es el valor mínimo que debe tomar la desviación estándar de las calificaciones, tal que la probabilidad de que esto ocurra sea 0.95. Esto significa que P(s ≥ K) = 0.95; de donde P(s < K ) = 0.05
Procedamos como antes
P(s < K ) = P(χ2(11) ≤ 0.11K2) = 0.05
En este punto debemos usar el procedimiento de la inversa en Chi - Cuadrado; pero como MS Excel no tiene esta herramienta, disponemos de un libro que contiene los valores de la Chi-Cuadrado para un determinado valor de los grados de libertad y una determinada probabilidad.
Es suficiente abrir el libro ValorInv ChiCuadrado y luego ejecutar una macro usando el método abreviado: [Ctrl]+i.
Completar los datos en el formulario que se activa y presionar [Enter] o hacer clic en [Aceptar]. Cuando desee terminar, simplemente haga clic en [Aceptar].
Según esto el valor obtenido es 4.5748; con lo cual tendremos:
0.11K2 = 4.5748, despejando K, obtenemos K = 6.449.
Nota:
No se olvide de usar el archivo ValorInv ChiCuadrado toda vez que necesite obtener el valor de Chi – cuadrado para una determinada probabilidad y un determinado grado de libertad.
Ejemplo 11
Se sabe que el tiempo que necesita un cajero en la ventanilla de un banco para atender a un cliente es una variable aleatoria normal con = 1.5 minutos. Este cajero es observado en la atención de 25 clientes seleccionados al azar.
a) Determine la media y la varianza de s² (varianza muestral)
b) Qué valor máximo tomará la desviación muestral, con probabilidad 0.975?
Solución
Sea X: Tiempo necesario para atender a un cliente
Recordemos que s2= (∑(Xi -  )2/(n-1) .
)2/(n-1) .
De esta ecuación, podemos despejar la sumatoria y tener ∑(Xi -  )2 =(n-1)s2
)2 =(n-1)s2
a) Hallaremos primero la media o valor esperado de s2.

b) Si K representa el valor máximo que toma la desviación estándar de la muestra, entonces se tiene que P(s ≤ K) = 0.975
Como ya hemos visto, P(s ≤ K)= P(s2 ≤ K2 )=P(χ2(n-1) ≤ ((n-1) K2)/σ2 )= 0.975
Reemplazando valores n y σ2 y simplificando, tenemos P(χ2(24) ≤ 10.67K2 )= 0.975
Para hallar el valor de K abriremos el archivo ValorInv ChiCuadrado,
Ejecutamos la macro usando el método abreviado: [Ctrl]+i
Digitamos los grados de libertad 24 y la probabilidad 0.975 y obtenemos 39.439
Y despejando K de 10.67K2 = 39.439 encontramos K = 1.9226.
Ejemplo 12
Una máquina embotelladora puede regularse de tal manera que llene un promedio de onzas por botella. Se ha observado que las onzas de contenido que vacía la máquina embotelladora tiene una distribución normal con = 1 onzas.
Supóngase que se selecciona una muestra aleatoria de 10 botellas y se mide el contenido de cada botella. Usando las 10 observaciones hallar los números b1 y b2 tales que P(b1 ≤ s 2 ≤ b2 ) = 0.9.
(Sugerencia: Suponga que el 90% se encuentra en la parte central de la distribución a usar).
Solución
Dado P(b11 ≤ s 2 ≤ b2 ) = 0.9, para encontrar los extremos por Chi-Cuadrado, debemos realizar la transformación de s2 hacia una variable Chi.Cuadrado.
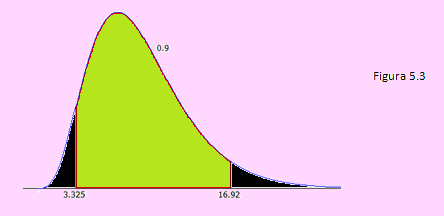
P(b1 ≤ s2 ≤ b2 ) = P(9b1/1 ≤ ((n-1) s2)/σ2 ≤ 9 b2/1)= P(9b1 ≤ χ2 (9) ≤ 9 b2)= 0.90
Según sabemos: P(χ2 (9) ≤ 9b1 )=0.05 y P( χ2(9) ≤ 9b2 )=0.95
Usando [Ctrl]+i en el archivo mencionado en el ejemplo anterior hallaremos 9b1 = 3.325 de de donde b1 = 0.3694
Del mismo modo, 9b2 = 16.918 de donde b2 = 1.8798
Valores Chi-Cuadrado se muestra en el siguiente gráfico
Ejemplo 13
AirCon S.A. desea adquirir dispositivos electrónicos en el cual la varianza de las resistencias no debe exceder los 0.40 ohmios2. Para evitar la aceptación de remesas que no cumplen con esta especificación, el departamento de control de calidad toma una muestra aleatoria de 25 componentes de cada remesa y mide la resistencia de cada uno.
Si la varianza de la muestra es demasiado grande, el departamento rechaza el pedido. Se considera que una varianza muestral es demasiado grande si la probabilidad de que ocurra esto es superior a 0.02. Se acaba de seleccionar una muestra de una remesa y se obtiene s2 = 0.75. Debe aceptarse la remesa?
Solución
De acuerdo al problema: n = 25; σ2 = 0.40; s2 = 0.75
Si P(s2 > 0.75) > 0.02 entonces se debe rechazar la remesa.
P(s2 > 0.75)= 1 - P(χ2(24) ≤ 24(0.75)/0.4) = 1 - P(χ2 (24) ≤ 45)=0.005875
Puesto que la probabilidad es inferior a 0.02, se debe aceptar la remesa.
Siguiente sesión.
 1,
1,  2 ,…,
2 ,…, k son las medias muestrales de cada una de las muestras, entonces podemos afirmar que
k son las medias muestrales de cada una de las muestras, entonces podemos afirmar que  , media aritmética de las medias muestrales, es una variable aleatoria definida como Media muestral.
, media aritmética de las medias muestrales, es una variable aleatoria definida como Media muestral. una variable aleatoria, entonces debe tener una distribución de probabilidad la cual estará definida por su media μ
una variable aleatoria, entonces debe tener una distribución de probabilidad la cual estará definida por su media μ y su varianza σ2
y su varianza σ2 , donde
, donde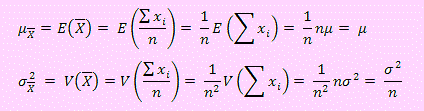
 una variable aleatoria y tiene una distribución de probabilidad, es natural preguntarnos: ¿Se puede calcular P(
una variable aleatoria y tiene una distribución de probabilidad, es natural preguntarnos: ¿Se puede calcular P( ≤ k)?
≤ k)? es la media muestral, entonces Z= (
es la media muestral, entonces Z= ( - μ)/(σ/ √n) es una variable normal estándar, siempre que n sea suficientemente grande (n ≥ 30).
- μ)/(σ/ √n) es una variable normal estándar, siempre que n sea suficientemente grande (n ≥ 30).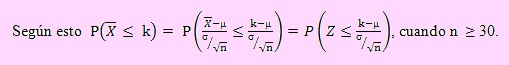
 = μ y σ2
= μ y σ2 = σ2/n, según la deducción realizada líneas arriba. Luego
= σ2/n, según la deducción realizada líneas arriba. Luego  → N(μ , σ2/n).
→ N(μ , σ2/n). - μ )/(s/√n) → t(n-1). Esto es, cuando la varianza poblacional no sea conocida, usaremos la distribución t de Student para resolver el problema.
- μ )/(s/√n) → t(n-1). Esto es, cuando la varianza poblacional no sea conocida, usaremos la distribución t de Student para resolver el problema. - μ | ≤ 100.
- μ | ≤ 100. - μ |≤100 )= P(μ -100 ≤
- μ |≤100 )= P(μ -100 ≤  ≤ μ + 100)=P(3400 ≤ μ ≤ 3600)= F(3600) – F(3400)
≤ μ + 100)=P(3400 ≤ μ ≤ 3600)= F(3600) – F(3400)
 .
. = (∑Xi / n = Promedio(B2:B13) = 128.167
= (∑Xi / n = Promedio(B2:B13) = 128.167 > 128.167).
> 128.167). - μ)/(s/√n) talque T → t(n-1)
- μ)/(s/√n) talque T → t(n-1)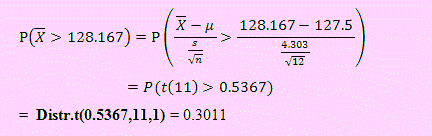
 – μ | ≤ 2).
– μ | ≤ 2). – μ | ≤ 2) = P(-2 + 127.5 ≤
– μ | ≤ 2) = P(-2 + 127.5 ≤  ≤ 2 + 127.5 )=P( 125.5 ≤
≤ 2 + 127.5 )=P( 125.5 ≤  ≤ 129.5)
≤ 129.5) a una variable t(n-1), tenemos
a una variable t(n-1), tenemos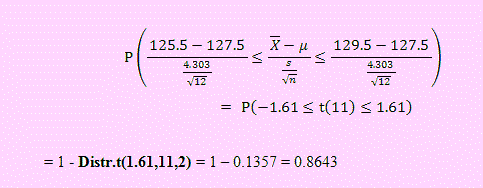
 ≤ 302.
≤ 302. ≤ 302)
≤ 302) 0 =301.5 y s = 7.5, usando la distribución t de Student tendremos:
0 =301.5 y s = 7.5, usando la distribución t de Student tendremos: