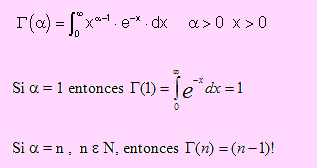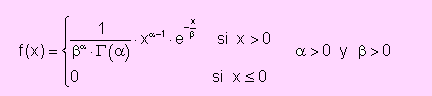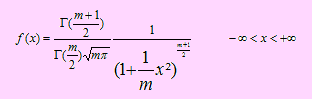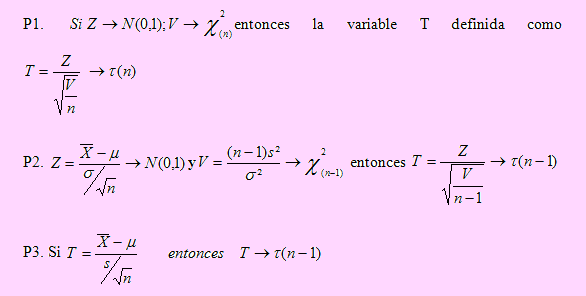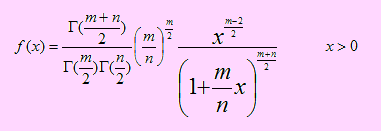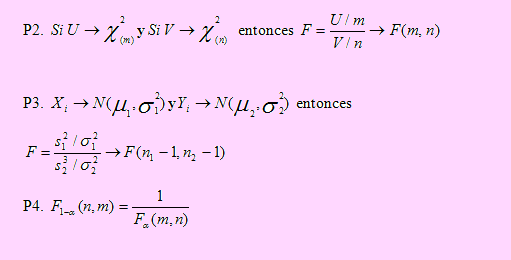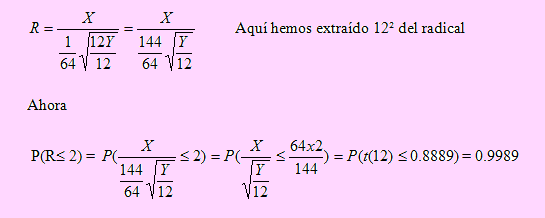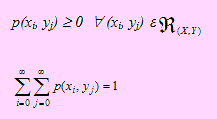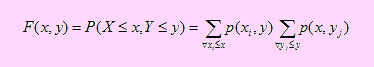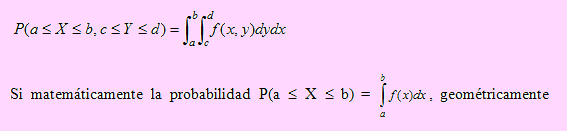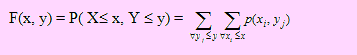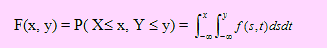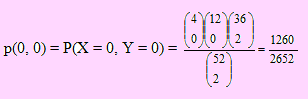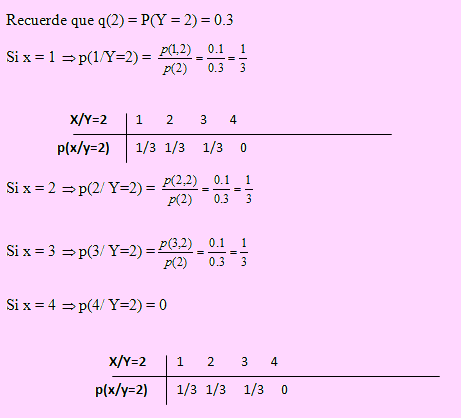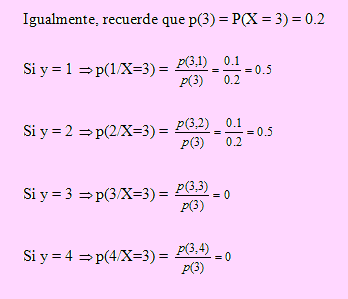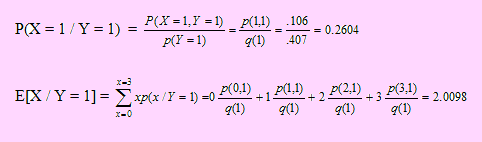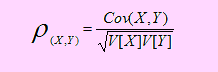4.13 OTRAS DISTRIBUCIONES CONTINUAS
La estadística dispone de otras variables aleatorias con distribuciones conocidas las que por lo general son útiles en la aplicación de problemas de muestreo, cuando el tamaño de muestra es pequeño; es decir, cuando no se puede aplicar el TLC.
Estas distribuciones son:
χ2 : La distribución Chi – cuadrado
t : La distribución t de Student
F : La distribución F de Fisher
Haremos un estudio muy breve de cada una de ellas y emplearemos el Excel para resolver problemas de probabilidad; y más tarde volveremos a usarlas para resolver problemas de muestreo y distribución muestral en los casos en que el tamaño de muestra sea pequeño. Para ello empezaremos definiendo la distribución Gamma ya que, como veremos, las anteriores son derivaciones de ésta. Función gamma Diremos que f es la función gamma si se cumple que
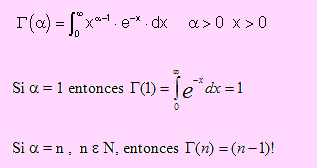
Distribución gamma
Sea X una variable aleatoria continua. Diremos que X es una variable que tiene distribución Gamma, de parámetros α y β, si su función de densidad de probabilidad viene dada por
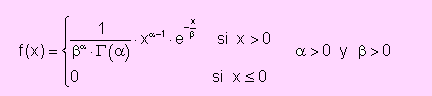
y lo denotaremos por X $rarr; G(α , β)
donde τ(α) es la función Gamma.
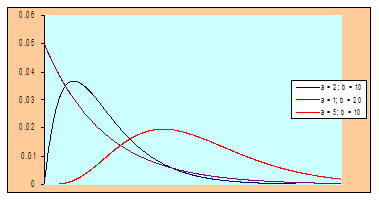
Un esbozo de la gráfica de esta distribución es la siguiente:
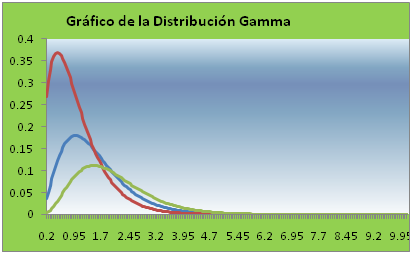
En la cual se muestra la gráfica para distintos valores del parámetro α.
Propiedades
P1. Si X %rarr; G(α, β) entonces µ= α β y σ2 = α β2
P2. Si X → G(α, β) y α = 1 entonces X se define como una variable con distribución exponencial de parámetro 1/β
Nota
Estas gráficas se han construido usando el programa Excel. Para ver cómo se han elaborado, abra el archivo Gráfica de Gráfica de Chi - t - F.
Otra gráfica:
La siguiente figura muestra la gráfica de la distribución gamma para diferentes valores de sus parámetros, construidos en MS Excel.
Distribución chi – cuadrado: χ2
Sea X una variable aleatoria. Diremos que X tiene distribución Chi – cuadrado a la que denotaremos por X → χ2 , donde v es el parámetro, si su función de densidad viene dada por
Observación:
Esta distribución también es un caso particular de la distribución gamma, en la cual hemos hecho β = 2 y α = v/2.
Propiedades
P1. Si X → χ2(v) entonces μ = v y σ = 2v ; donde v representa los grados de libertad de la distribución.
P2. Si Z → N(0, 1) entonces Z2 → χ2 (1)

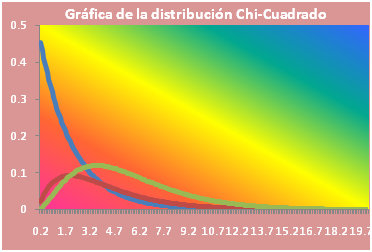
Su gráfica es

Obsérvese que, a diferencia de la normal, ésta no es una distribución simétrica. La distribución sólo toma valores positivos.
Distribución t de student
Sea X una variable aleatoria continua. Diremos que X tiene distribución t de Student lo que denotaremos por T t(m), si su función de densidad viene dada por
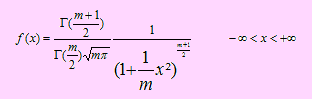
donde el parámetro m representa los grados de libertad.
La gráfica de esta distribución se muestra en la figura
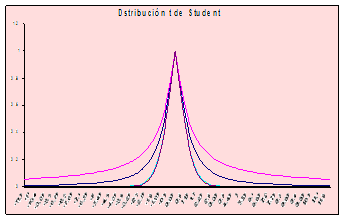
Observación 1:
Si expandimos los valores de la variable en los alrededores de su valor central, la gráfica podría presentar un máximo bastante suavizado visualizándose como la campana de Gauss.
Esto se aprecia en la siguiente figura
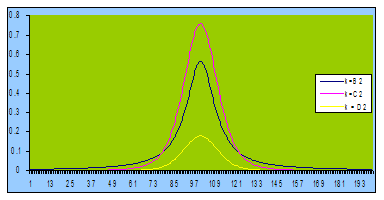
Observación 2
Como se puede apreciar en la definición, esta función es simétrica y gozar por tanto de la misma propiedad de una variable normal: P(-a < X < a) = 2 F(a) -1
Teorema
Si X → t(m) entonces μ = 0 y σ2 = m/(m-2) , m > 2 Propiedades
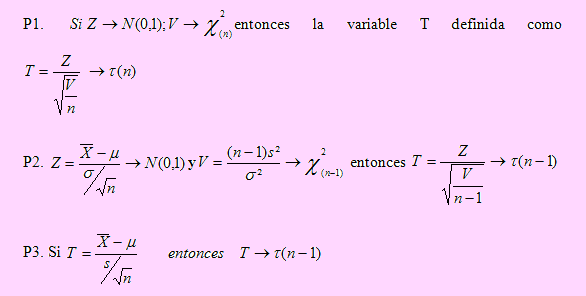
Distribución f de Fisher
Sea X una variable aleatoria continua con f su función de densidad de probabilidad. Diremos que X tiene distribución F de Fisher y lo denotaremos por X → F(n, m) con n número de grados de libertad del numerador y m número de grados de libertad del denominador, cuya función de densidad es la siguiente:
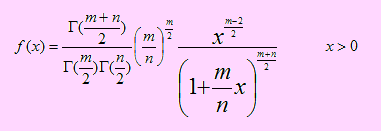
donde τ(.) es la función Gamma.
La gráfica de esta distribución se puede apreciar en la siguiente figura
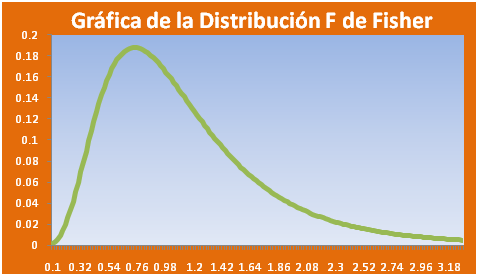
Propiedades
P1. Si X → F(m, n) entonces μ = n /(n-2) y σ = [2n(n+m-2)] /[ m(n-2)2(n-4)], n>4; donde n representa los grados de libertad del numerador y m los grados de libertad del denominador.
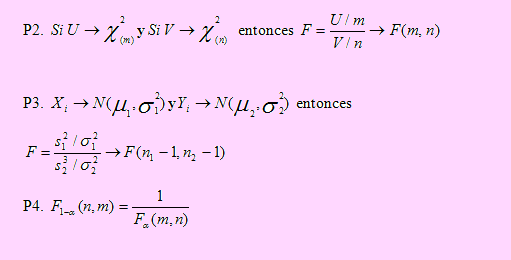
Ejemplos usando el programa Excel:
El programa Excel dispone de las siguientes funciones referidas a estas distribuciones continuas.
|
Distribución Gamma
|
|
Para calcular P(X ≤ K)
|
=Distr.Gamma(K,α, β,tipo)
Donde α y β son los parámetros y tipo=1 para acumulada.
|
|
Para hallar K si P(X ≤ K) = p
|
=Distr.Gamma.Inv(p, α, β)
|
|
Distribución Chi – cuadrado
|
|
Para calcular P(X ≤ K)
|
=1-Distr.Chi(K,gl)
Donde gl representa los grados de libertad
|
|
Para hallar K si P(X ≤ K) = p
|
Excel no dispone de una función para resolver este problema.Para ello hemos creado un procedimiento que se encuentra en el archivo Valor invChi. Para usarlo es suficiente usar el método abreviado:
[Ctrl]+i
|
|
Distribución t de Student
|
|
Para calcular P(X ≤ K)
|
=1-2*Distr.t(K,gl,2)
donde 2 indica doble cola.
|
|
Para hallar K si P(X ≤ K) = p
|
=Distr.t.inv(2*p,gl)
|
|
Distribución F de Fisher
|
|
Para calcular P(X ≤ K)
|
=1-Distr.f(K,gln,gld)
donde gln: grados de lib. en el numerador
gld: grados de lib. en el denominador.
|
|
Para hallar K si P(X ≤ K) = p
|
=Distr.F.Inv(1-p,gln,gld)
|
Ejemplos de aplicación directa:
A continuación presentaremos algunos ejemplos directos que no merecen mayor comentario ni procedimiento:
Para una variable aleatoria X, con distribución Chi-Cuadrado con 15 gl, encuentre:
a) P(X < 3.89) b) P (X > 12.495 ) c) P( 1.58 < X < 10 )
Rpta: a) 0.0019243 b) 1-0.358759 c) 0.180260 - 0.0000061
Para una distribución Chi-Cuadrado, encuentre el valor de a, en cada caso:
a) P(χ2(8) < a ) = 0.95; b) P(χ2(10) > a) = 0.5; c) P( χ2(18) > a) = 0.99
Rpta. a) 15.5073 b) 18.3070 c) 7.01491
Para una variable aleatoria X con distribución t de Student,con 20 grados de libertad, encuentre:
a) P(X < -1.594) b) P(X > 2.49) c) P(-1.58 < X < 1) d)P(|X| >1.89)
Rpta. a) 0.0633089 b) 1-0.989154 c) 0.835372 – 0.0648966 d) 0.07334
Para una distribución t de Student, encuentre el valor de a en cada caso:
a) P(t(10)> a) = 0.025 b) P( t(15)> a ) = 0.10 c) P(1.476 < t(5) < a) = 0.075
Rpta. a) 2.22814 b) 0.34061 c) F(a) = 0.075 + F(1.476) ; a = 0.81283
Para una variable aleatoria X con distribución F, con 5 grados de libertad en el numerador y 8 grados de libertad en el denominador, encuentre
a) P(X < 2.86) b) P(X > 0.875) c) P(0.25 < X < 3.84 ) d) P(| X | < 5)
Rpta. a) 0.909794 b) 1-0.462061 c) 0.95478 – 0.0716954 d) 0.977426
Para una distribución F, encuentre el valor de a, en cada caso:
a) P(F(12,9) < a)= 0.4785 b) P(F(14,16)> a)=0.2475 c) P(a < F(21,19) < 2.5) = 0.9584
Rpta. a) 0.984888 b) 1.42265 c) F(a) = F(2.5) - 0.9584; a = 0.01694
En cada uno de los siguientes casos, hallar la probabilidad correspondiente:
Si X → χ2(17) , hallar a y b tal que P( a< X < b ) = 0.88 y P( X > b ) = 0.02
Sugerencia:
Primero encuentre b, luego resuelva P(a < X < a) = 0.88
Si X → t(9), hallar P(X ≥ 1.1), P(-0.703 ≤ X ≤ 4.297 ) , P( X ≤ -2.398)
Si X → t(6), hallar c tal que P(X > c) = 0.10
Si X → F(4,5), hallar P(X ≥: 5.19 ) , P( 3.52 ≤ X ≤ 15.56) , P(X ≤ 7.39)
Si X → F(2,3), hallar c de tal manera que P( X ≥ c ) = 0.05
Abra el archivo Grafica de chi-t-F. Observe la forma de la gráfica de cada una de las distribuciones. Modifique el valor de los parámetros de las distribuciones Chi – Cuadrado y t de Student y observe cuándo su comportamiento es aproximadamente normal.
Modifique los valores de los grados de libertad y observe la gráfica resultante. ¿Qué conclusión obtiene si los grados de libertad (directamente relacionados con el tamaño de muestra) se incrementan?.
Tomando en cuenta las gráficas que se muestran en el archivo del ejercicio anterior, ¿cuál de estas distribuciones es simétrica respecto al eje Y?
¿En cuál de estas distribuciones se puede aplicar las siguientes propiedades de la distribución acumulada?:
F(-k) = P(Z ≤ -k ) = P(Z > k) = 1- P(Z ≤ k ) = 1 – F(k)
P(-k ≤ Z ≤ z ) = 2 F(k) -1
Ejemplo 156
Sean X, Y, W, U variables aleatorias independientes tales que X → N(40, 25);
Y → χ² (10); W → χ² (5); U → t(7).
a) Hallar el valor de k tal que:
P[ (X - 40)² > k ] = 0.10
Como X → N(40, 25), al dividir la expresión entre 25 obtenemos
P((X-40)2/40 > k/25) = 0.10 de donde P((X-40)/5)2>k/25) = 0.10
La expresión del primer miembro es Z² lo cual, según la propiedad 2 de χ² se distribuye χ² con un grado de libertad.
Por tanto P(χ² (1) > k/25 ) =.10
De donde P(χ² ≤ k/25 ) = 0.90
Usando el archivo Valor invChi encontramos k = 67.6385
b) Hallar P(k < W + Y < 27.488 ) = 0.95
En este caso las W e Y tienen distribución χ² y como son dos variables, el número de grados es de libertad es 2. Luego P( k < χ² (12) < 27.488 ) = 0.95
Esto significa que F(27.488)-F(k) = 0.95 ⇒ F(k) = 0.974997 – 0.95
De donde k = 6.262. Hemos usado grados de libertad = 5 + 10 = 15
c) Encuentre P( W/Y < k)) = 0.90
Qué variable se genera al dividir dos variables que son χ² ?
Al dividir al numerador entre 5 y al denominador entre 10, logramos construir una nueva variable de la forma: T = (W/5) / (Y/10); según esto, T tiene una distribución F de Fisher; por tanto, logramos obtener una F(5, 10)
d) Hallar k talque P( | U | > k ) = 0.20
P(|U|<= k ) = 0.80 ⇒ P(-k < U < k) = 0.80) ⇒ 2f(k)-1=0.8; de donde f(k) = 0.9
Ejemplo 157
Si X → χ2(12) resuelva las siguientes preguntas:
P(X ≤ 5)
P(X ≥ 5)
Encuentre el valor de k tal que P(8 ≤ X < k) = 0.95
Solución
Usando la distribución acumulada de la distribución Chi-cuadrado, tenemos
P(X ≤ 5) = F(5) = 0.04202
P(X ≥ 15) = 1 – P(X < 15 ) = 1 – 0.75856 = 0.24146
Como P(8 ≤ X < k ) = F(k) – F(8)
entonces F(k) – F(8) = 0.65 Como F(8) = P(X ≤ 8) = 0.21487
Entonces F(k) – 0.21487 = 0.65
De donde F(k) = 0.86487
Usando el archivo mencionado en a) se puede encontrar el valor de k.
Ejemplo 158
Si X → N(0, 1), Y → χ²(8) y R = X / √(Y/8); obtenga P(R ≤ 2)
Solución
Observando la propiedad 1 de la distribución t de Student podemos ver que R es un cociente de una N(0, 1) y la raíz de una Chi – cuadrado que está dividida por su grado de libertad; en consecuencia R tiene distribución t(8) y luego P(R ≤ 2) = P(t(8) ≤ 2) = 0.959742
Ejemplo 159
Si X → N(0, 1), Y → t(12) y R = X / √ (Y/8), Obtenga P(R ≤ 2).
Solución
En este caso, en lugar de 8 que divide a Y debiera estar 12, que son los grados de libertad de Y. Extraeremos 1/8 del radical y multiplicaremos a Y por 12 y dividiremos entre 12, como se muestra a continuación
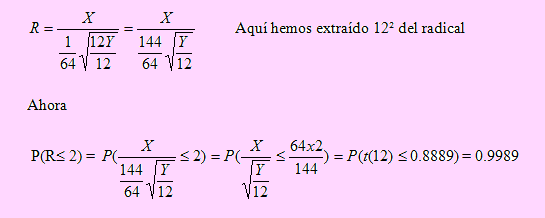
Ejemplo 160
Las variables X , Y , W son independientes con distribuciones respectivas:
X → χ2(10), , Y → t(20), W → χ2(15).
Hallar :
Los valores de c y k tal que: P(c < X < k) = 0.94 si P(X > k) = 0.015.
P(|Y| < 2.04)
El valor de h de modo que: P(h < X + W < 34.3816) = 0.65
Solución
Si P(X > k ) = 0.015 ⇒ P(X ≤ k) = 0.985. Por Inverse en Chi – cuadrado, se tiene k = 22.0206
P(|Y| < 2.04 ) = P(-2.04 < Y < 2.04 ) = t(20)(2.04) – t(20)(-2.04) = 0.9452
Siendo X y W variables Chi-Cuadrado, entonces X+W → χ2(25) y P(h < X + W < 32.3819)=0.65,
tenemos P(h < χ2(25) < 32.3816) = 0.65
De donde χ2(25)(32.3816) - χ2(25)(h) = 0.65. Usando Minitab obtenemos: 0.872735 - χ²(25)(h) = 0.65 . Simplificando χ²(25)(h) = 0.222735. Y usando inverse en Chi – cuadrado, encontramos h = 19.4057

Solución

4.14 VARIABLES ALEATORIAS BIDIMENSIONALES
Definición
Sea ζ un experimento aleatorio y Ω el espacio muestral asociado a ζ. Sean también X = X(s) y Y = Y(s) dos funciones que asignan un número real a cada resultado s del experimento, contenido en el espacio muestral; es decir, para cada sS existe un número real x para el cual x = X(s) y también un número real y tal que y = Y(s). Bajo estas consideraciones diremos que (X, Y) recibe el nombre de variable aleatoria bidimensional.
Observaciones
1. En el gráfico podemos apreciar que si Ω es el espacio muestral asociado a ζ, entonces, la variable aleatoria X tomará los valores x1, x2, ... xn .
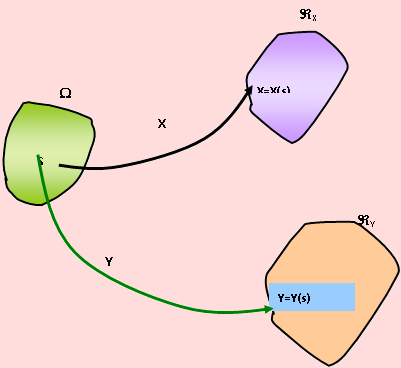
2. Así como las variables aleatorias X e Y tienen su espacio rango ℜX y ℜY, respectivamente, así también la variable aleatoria bidimensional (X, Y) tiene su espacio rango ℜ (X, Y).
3. El espacio rango de (X, Y), es un conjunto formado por pares ordenados del plano cartesiano.
4. La observación anterior nos sugiere entonces que, si las variables aleatorias X e Y pueden ser discretas o continuas, la variable aleatoria bidimensional (X, Y) también puede ser discreta o continua.
5. Nuevamente remitiéndonos a la observación anterior, en el caso de que (X, Y) sea una variable bidimensional discreta, su espacio rango será un conjunto de retículas (o nodos de una red) del plano cartesiano; en cambio si (X, Y) es una variable continua, su espacio rango será una región continua del plano cartesiano y será una parte del producto de los intervalos [a, b] x [c, d] ∈ R² donde a ≤ X ≤ b y c ≤ Y ≤ d.
Tipos de Variable Aleatoria
Diremos que (X, Y) es una variable aleatoria bidimensional discreta si el conjunto de los valores posibles de la variable es finito o numerablemente infinito. Este conjunto, llamado espacio rango ℜ(X, Y) es un conjunto reticular.
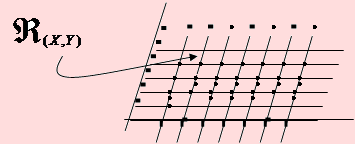
Los valores posibles de (X, Y) pueden ser representados como pares ordenados (xi, yj) para i = 1, 2, ..., n, ... y j = 1, 2, ..., m, ...
Diremos que (X, Y) es una variable aleatoria bidimensional continua si el conjunto de los valores posibles de la variable es un conjunto infinito. Este con junto constituye una región en el plano cartesiano, como se muestra en la siguiente figura
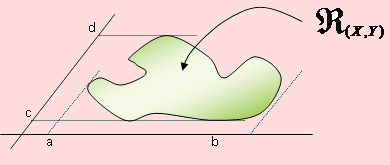
Los valores que la variable aleatoria bidimensional toma, pertenecen a una región ℜ(X, Y) del plano cartesiano tales que ℜ(X, Y) = { (x, y) / a ≤ x ≤ b, c ≤ y ≤ d }.
Distribución de probabilidad para (X, Y)
Caso 1: variable aleatoria bidimensional discreta
Sea (X, Y) una variable aleatoria bidimensional discreta, con ℜ(X, Y) su espacio rango. Si p(xi, yj) es una función tal que a cada par (xi, yj) le asigna el número real P(X = xi, Y = yj) diremos entonces que p(xi, yj) es función de probabilidad conjunta de (X, Y), siempre que cumpla las siguientes condiciones:
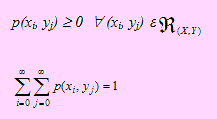
Observaciones
p(xi, yj) = P(X = xi, Y = yj) es la probabilidad de que ocurra el evento compuesto { X = xi , Y = yj } i = 1, 2, 3, ..., n, ... ; j = 1, 2, 3, ..., m, ...
La gráfica de la función de probabilidad de (X, Y), como en el caso unidimensional, son barras verticales al valor de la variable.
Como en este caso el espacio rango es un espacio reticulado, el valor de probabilidad para un valor de la variable será una barra perpendicular en el nodo correspondiente, como se puede apreciar en la siguiente figura.
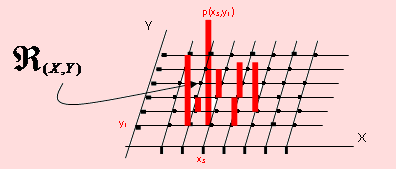
La función de probabilidad conjunta de (X, Y) se presenta, por lo general, en forma de un cuadro de distribución de doble entrada. Los valores de las variables X e Y se colocan en las primeras filas o columnas y en el centro del mismo, el valor de sus respectivas probabilidades, como se muestra en la siguiente figura

La distribución acumulada en el caso discreto
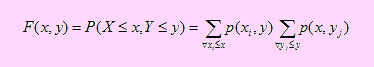
Ejemplo 162
Sea (X, Y) una variable aleatoria bidimensional cuya función de probabilidad conjunta viene dado en el siguiente cuadro.
| X \ Y |
0 |
1 |
2 |
3 |
4 |
| 0 |
0.01 |
0.11 |
0.0 |
0.10 |
0.05 |
| 1 |
0.12 |
0.01 |
0.12 |
0.04 |
0.01 |
| 2 |
0.09 |
0.08 |
0.0 |
0.12 |
0.03 |
| 3 |
0.01 |
0.05 |
0.02 |
0.0 |
0.03 |
Encuentre las siguientes probabilidades:
a) p(0, 3) b) P(X<3, Y = 2) c) P(X > 0, Y ≥ 2)
d) P(X = 2) e) P( Y = 2)
Solución
a) p(0, 3) = P(X = 0, Y = 3) = 0.01
b) P(X<3, Y = 2) es la suma de todas las probabilidades conjuntas cuando la variable X toma valores X = 0, 1 y 2; mientras que Y toma valores Y = 2; es decir que P(X<3, Y = 2) = p(0, 2) + p(1, 2) + p(2, 2) = 0.09 + 0.08 + 0.00 = 0.17
c) En este caso es más cómodo usar complementos:
P(X>0, Y ≥ 2) = p(1,2) + p(1,3) + p(2,2) + p(2,3) + p(3,2) +...+ p(4,3) = 0.33
d) P(X = 2) es la probabilidad de que ocurra el evento { X = 2 }. Pero este evento ocurre cuando Y = 1; también ocurre cuando Y = 2 o cuando Y = 5 o Y = 9; por lo que, P(X = 2) = 0.0 + 0.12 + 0.0 + 0.02 = 0.14
e) Del mismo modo, P(Y = 2 ) = 0.09 + 0.08 + 0.0 + 0.12 + 0.03 = 0.32. Aquí también cuando Y = 2, la variable X toma todos los valores de su recorrido: 0, 1, 2, 3, 4.
Ejemplo 163
Una urna contiene 3 bolas numeradas 1, 2, 3, respectivamente. De la urna se extraen dos bolas, una después de otra, sin reposición. Sea X el número de la primera bola extraída y Yel número de la segunda bola. Hallar la distribución de probabilidad conjunta de (X, Y).
| X \ Y |
1 |
2 |
3 |
| 1 |
0.0 |
1/6 |
1/6 |
| 2 |
1/6 |
0.0 |
1/6 |
| 3 |
1/6 |
1/6 |
0.0 |
Solución
Sea X la variable aleatoria definida como “El número de la primera bola extraída”.
Sea Y la variable aleatoria definida como “El número de la segunda bola extraída”.
Según esto: X = 1, 2, 3; Y = 1, 2, 3. Por lo que el espacio rango de (X, Y) es el conjunto {(1, 2), (1, 3), (2, 1), (2, 3), (3, 1), (3, 2) }.
Hallemos cada una de las probabilidades individuales
p(1, 1) = 0; es decir, es imposible que ocurra el evento X = 1, Y = 1, sin reposición.
Del mismo modo, p(2, 2) = 0 y p(3, 3) = 0, por ser eventos imposibles
p(1, 2) = 1/6 p(1, 3) = 1/6 p(2, 1) = 1/6, .... p(3, 2) = 1/6
Ejemplo 164
Suponga que tres objetos no diferenciables se distribuyen al azar en tres celdas numeradas. Sea X el número de celdas vacías e Y el número de objetos colocados en la primera celda. Construya la tabla de distribución de probabilidad conjunta de (X, Y).
Solución
Si X es la variable definida como “El número de celdas vacías” y Y se define como “El número de objetos colocados en la primera celda” entonces X = 0, 1, 2 y Y = 0, 1, 2, 3.
Puesto que 0, 1, 2 ó los 3 objetos pueden caer en cualquiera de las tres celdas, y del mismo modo, cualquier celda puede contener 0, 1, 2 ó los tres objetos, el número de casos posibles será 33 = 27. Debemos hallar el número de casos favorables en cada caso.
p(0, 0) = P(X=0, Y=0). Significa que hay 0 celdas vacías y hay 0 objetos en la primera. Esto es imposible por lo que p(0, 0) = 0.
p(0, 1) = P(X=0, Y=1). Significa que todas las celdas están ocupadas y que la primera tiene un objeto. El esquema siguiente muestra las diversas situaciones que puede presentarse:
La primera celda puede ser ocupada por cualquiera de los tres objetos, la segunda por dos de ellos y la tercera sólo por uno. Esto es P(3, 3) = 6.
Por ello p(0, 1) = 6/27
p(0, 2) = P(X=0, Y=2) significa que hay cero celdas vacías y que la primera contiene dos objetos.
Esto es imposible por ello p(0, 2) = 0.
p(0, 3) = P(X = 0, Y = 3) = 0, por la misma razón
p(1, 0) = P(X = 1, Y = 0) significa que la hay una celda vacía y que la primera debe tener 0 objetos. En este caso los objetos deben repartirse en las dos celdas, por ello p(1, 0) = 6/27
p(1, 1) = P(X = 1, Y=1) significa que debe haber una celda vacía y la primera debe contener un objeto.
Como la primera debe contener un objeto, hay dos posibilidades de tener una celda vacía. Puesto que la primera celda puede ser ocupada de 3 formas diferentes, el número de maneras de obtener un objeto en la primera y una de las restantes vacías, es 3 x 2, por ello p(1,1) = 6/27.
Encontremos ahora p(1,2) = P(X = 1,Y = 2).
El razonamiento es similar a p(1,1) excepto que la celda con 0 objetos puede ser cualquiera de las restantes p(1,2) = 6/27.
p(1,3) = P( X = 1, Y = 3) este es un evento imposible por lo que p(1, 3) = 0.
p(2, 0) = P(X =2, Y = 0) . Esto significa que debe haber 2 celdas vacías y la primera debe contener 0 objetos. Como la primera ya está vacía, la segunda vacía puede ser la segunda celda o la tercera: dos posibilidades; por ello p(2, 0) = 2/27
p(2,1)=P(X = 2, Y = 1). Dos celdas vacías y la primera con un objeto es p(2, 1) = 0
p(2,2) = P(X =2,Y = 2) Igualmente p(2, 2) = 0
p(2,3) = P(X =2, Y =3) = 1/27. Si tiene sentido. Los tres objetos están en la primera.
| X \ Y |
0 |
1 |
2 |
| 0 |
0.0 |
6/27 |
2/27 |
| 1 |
6/27 |
6/27 |
0.0 |
| 2 |
0.0 |
6/27 |
0.0 |
| 3 |
0.0 |
0 |
1/27 |
Ejemplo 165
Se elige aleatoriamente uno de los números enteros 1, 2, 3, 4, 5. Después de eliminar todos los números enteros menores que el elegido(si hubiera), se elige uno de los restantes. Sean X e Y los números elegidos en la primera y segunda elección, respectivamente.
Determine la distribución de probabilidad conjunta de X e Y y calcule P(X + Y > 7) y P(Y – X > 0
Solución
Definamos a X como “El número elegido en la primera vez” e Y, “El número elegido en la segunda vez”.
Veamos un ejemplo de cómo se realiza el experimento:
Supongamos que en la primera elección se elige al dígito 3. Según el problema, se debe eliminar los dígitos 1 y 2, que son menores que el elegido, 3. La segunda elección se hace teniendo disponibles los dígitos 3, 4 y 5. Esto quiere decir que los valores que tomará X son: 1, 2, 3, 4, 5. Los valores que pueda tomar Y son 1, 2, 3, 4, 5.
Encontremos las probabilidades individuales.
Antes de empezar, debemos tomar en cuenta que la primera elección se hace de un total de 5 por lo que la probabilidad de elegir cualquier dígito la primera vez siempre es 1/5.
La probabilidad de elegir el segundo número es 1/(5-k) donde k es el número de dígitos eliminados. Esto quiere decir que p(x, y) = 1/5 (1/(5-k)) y k: 0, 1, 2, 3, 4 representa el número de dígitos eliminados después de la primera elección.
La distribución de probabilidad en detalle se da en el siguiente cuadro.
| X \ Y |
1 |
2 |
3 |
4 |
5 |
| 1 |
1/25 |
0.01 |
0.0 |
0.0 |
0.0 |
| 2 |
1/25 |
1/20 |
0.0 |
0.0 |
0.0 |
| 3 |
1/25 |
1/20 |
1/15 |
0.0 |
0.0 |
| 4 |
1/25 |
1/20 |
1/15 |
1/10 |
0.0 |
| 5 |
1/25 |
1/20 |
1/15 |
1/10 |
1/5 |
Calculemos ahora las probabilidades pedidas
P(X+Y > 7 ): Los únicos pares que cumplen la condición X + Y > 7 es el conjunto B definido como B = {(x, y) / x + y > 7} = { p(3, 5), p(4, 4), p(4, 5), p(5, 3), p(5, 4), p(5, 5)}.
Luego P(B) = 19/30.
Del mismo modo, si A = {(x, y)/ y – x > 0 } entonces P(A) = 163/300
Caso 2: Variable aleatoria bidimensional continua
Sea (X, Y) una variable aleatoria bidimensional continua, con &real:(X, Y) ⊆ R2 su espacio rango. Diremos que f(x, y) es una función de densidad de probabilidad conjunta de (X, Y), siempre que f cumpla las siguientes condiciones:
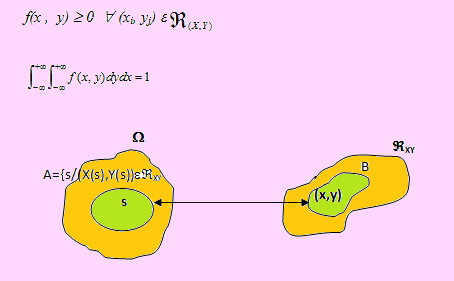
Observaciones De manera simplificada fdpc significará “función de densidad de probabilidad conjunta” Sin duda el intervalo al que correspondan X e Y será -∞< X < +∞ y -∞< Y < +∞.
En particular, X pertenecerá al intervalo (a, b) tal que a ≤ X ≤ b. Del mismo modo, Y pertenecerá al intervalo (c, d) tal que c ≤ Y ≤ d. La gráfica de la función f determina una superficie en el espacio, como se muestra en la siguiente figura.
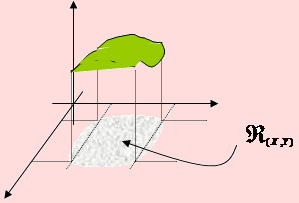
Eventos equivalentes
En la idea de simplificar el trabajo, daremos el concepto de eventos equivalentes como una observación. Si recordamos de las variables unidimensionales, la existencia de eventos equivalentes fue necesaria para la expansión de la teoría de probabilidades al espacio rango de X.
La existencia de eventos equivalentes es la bisagra que nos permite hablar de probabilidades de eventos definidos, en este caso por la ocurrencia conjunta de las variables X e Y.
Puesto que en la definición (X, Y) es una función que permite asignar valores (x,y) reales a elementos s del espacio muestral Ω entonces podemos definir la existencia de un evento A ⊆ Ω para el cual exista un evento B ⊆ ℜ(X, Y), tales que B = {(x,y) / (x,y) ∈ℜ(X, Y) } donde A = {s / (X(s), Y(s) ) ∈ B }. Según esto, los eventos A y B son eventos equivalentes.
Por ello P(B) = P(A), como se muestra en el esquema de la figura anterior.
De acuerdo a la observación anterior, la probabilidad de que ocurra el evento B, definido como B = {(x,y)/a ≤ x ≤ b, c ≤ y ≤ d } es igual a
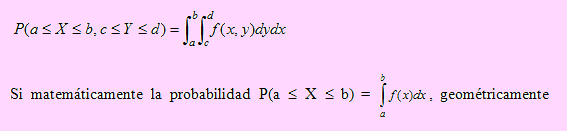
representa el área de una superficie sobre el plano cartesiano. En el caso bidimensional la probabilidad P(a ≤ X ≤ b, c ≤ Y ≤ d) geométricamente representa el volumen de una superficie en el espacio y definida por la gráfica de la curva f(x,y) y limitada por los intervalos a ≤ X ≤ b , c ≤ Y ≤ d y en el plano XY por la región ℜ(X, Y).
Distribución Acumulada de una variable aleatoria bidimensional
Caso Discreto
Si (X, Y) es una variable aleatoria bidimensional discreta con p(xi,yi) su función de probabilidad conjunta, diremos que F(x, y) es su función de distribución acumulada si
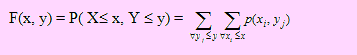
Caso Continuo:
Si (X, Y) es una variable aleatoria bidimensional continua con f(x, y) su función de densidad de probabilidad conjunta, diremos que F(x, y) es su función de distribución acumulada si
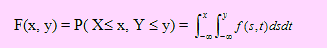
La evaluación de la distribución acumulada de (X, Y) es similar al caso unidimensional.
Distribuciones marginales
Caso discreto
Sea (X, Y) una variable aleatoria bidimensional discreta con p(xi, yj) su función de probabilidad conjunta, donde i = 1, 2, 3, ..., n y j = 1, 2, 3, ..., m. Diremos que p(xi) es la función de probabilidad marginal de X si p(xi) viene definida por

Observaciones
Una vez obtenida las distribuciones marginales podemos hallar el valor esperado de X, la varianza de X a partir de la distribución marginal de X.
Del mismo modo, teniendo la distribución marginal de Y podemos hallar el valor esperado y la varianza de Y.
La función de probabilidad de X, p(x), la obtendremos en la última fila en el cuadro de distribución de probabilidad conjunta.
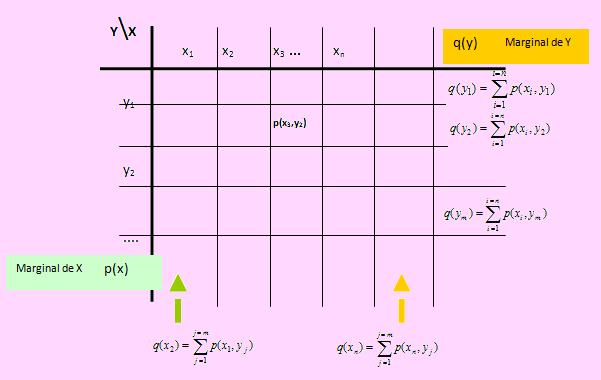
Igualmente, la distribución de probabilidad marginal de Y estará ubicada en la última columna de la misma. La suma de todos los valores de p(xi) es 1, i = 1, 2, 3, ..., n. Igualmente si sumamos todos los valores de q(yj) será igual a 1, con j = 1, 2, 3, ..., m.
Ejemplo 166
Encuentre las distribuciones marginales de X e Y, del Ejemplo 80.
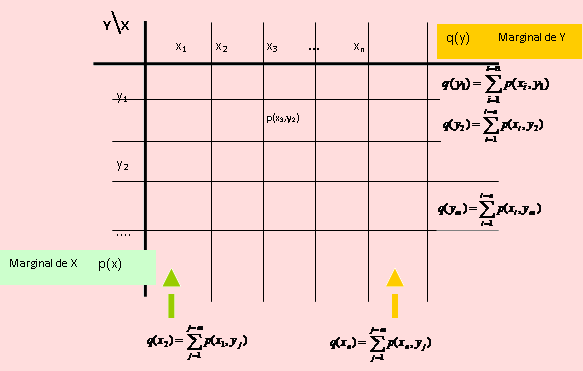
Solución
La distribución de probabilidades conjunta de (X, Y) es la que se muestra en el gráfico anterior.
A partir de ella, la distribución Marginal de X es:
Si X = 0 entonces p(0) = p(0, 1) + p(0, 2) + p(0, 3) = 6/27
Si X = 1 entonces p(1) = p(1, 1) + p(1, 2) + p(1, 3) = 18/27
Si X = 2 entonces p(0) = p(2, 1) + p(2, 2) + p(2, 3) = 3/27
Por lo que la función marginal de X, dado en forma tabular, es
| X |
0 |
1 |
2 |
| p(x) |
6/27 |
18/27 |
3/27 |
Esta misma distribución se aprecia en la última fila del cuadro de la distribución conjunta.
La distribución Marginal de Y es:
Si Y = 0 entonces q(0) = q(0, 0) + q(1, 0) + q(2, 0) = 8/27
Si Y = 1 entonces q(1) = q(0, 1) + q(1, 1) + q(2, 1) = 12/27
Si Y = 2 entonces q(2) = q(0, 2) + q(1, 2) + q(2, 2) = 6/27
Si Y = 3 entonces q(3) = q(0, 3) + q(1, 3) + q(2, 3) = 1/27
Por lo que la función marginal de X, dado en forma tabular, es
| Y |
0 |
1 |
2 |
3 |
| p(y) |
8/27 |
12/27 |
6/27 |
1/27 |
Esta misma distribución se aprecia en la última columna del cuadro de la distribución conjunta.
Ejemplo 167
La función de probabilidad conjunta de (X, Y) está dada por p(x, y) = (x2 + y2)/32, x = 0, 1, 2, 3 ; y = 0, 1
Encuentre las distribuciones marginales de X e Y, respectivamente.
Solución
Para la Marginal de X. sólo debemos reemplazar los valores de Y, para cada valor que tome X. Igualmente, para la Marginal de Y, reemplazamos valores de X, para cada valor de Y.
Marginal de X:
Puesto que el espacio rango de X es 0, 1, 2, 3 entonces
p(0) = p(0, 0) + p(0, 1) = 0 + 1/32;
p(1) = p(1, 0) + p(1, 1) = 1/32 + 2/32
p(2) = p(2, 0) + p(2, 1) = 4/32+5/32
p(3) = p(3, 0) + p(3, 1) = 9/32 + 10/32
Por ello la distribución marginal de X se muestra en el siguiente cuadro
| X |
0 |
1 |
2 |
3 |
| p(x) |
1/32 |
3/32 |
9/32 |
19/32 |
Otra forma de responder a la preguntas es la siguiente:

Ejemplo 168
Se extraen al azar 2 cartas de un naipe de 52 cartas, sin reemplazo. Sea X el número de ases que aparece e Y el número de espadas.
Obtener la distribución de probabilidad conjunta de (X, Y)
Obtener las distribuciones marginales de X e Y
Evalúe P( X > Y )
Solución
Definamos a X como “El número de ases que se extraen” e Y como “El número de espadas extraídas”, según el problema. Esto significa que X toma valores: 0, 1, 2 ; así como Y toma 0, 1 y 2. Con esto, el espacio rango de (X, Y) es fácil encontrarlo(el producto cartesiano).
Encontremos las probabilidades individuales:
p(0, 0) = P(X = 0, Y = 0) . Como se trata de extraer 0 ases de un total de 4, el número de maneras de obtenerlo es C(4,0).
Igualmente, 0 espadas se extrae de C(12,0) maneras. Hemos quitado una espada ya que el as de espadas no debe ser tomado en cuenta.
Hasta este punto, tenemos 0 ases + 0 espadas ; pero como se extraen 2 cartas, seguramente las cartas que “faltan” (las dos), deben ser cualquiera del naipe; estas se extraen de C(36, 2) maneras.
Luego: el número de maneras de extraer 0 ases “y” 0 espadas “y” 2 cartas cualquiera es C(4, 0) x C(12, 0) x C(36, 2), lo que constituye “el número de casos favorables a extraer 0 ases y 0 espadas. Por otro lado, el número de casos posibles de extraer 2 cartas viene dado por C(52, 2).
Por ello
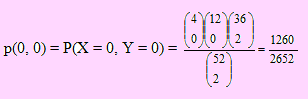
p(1, 0) = P(X = 1, Y = 0). Esto significa que no debe extraerse el as de espadas. Por ello, sólo quedan 3 ases disponibles. El número de casos favorables será C(3, 1)x C(12, 0) x C(36, 1).
Por ello p(1, 0) = 216/2652
p(2, 0) = P(X = 2, Y = 0). Esto significa extraer 2 ases, de los cuales ninguno debe ser el de espada, lo que hace disponible sólo a 3 de los ases. El número de maneras de lograr esto es C(3, 2) x C(12, 0) x C(36, 0).
Luego p(2,0) = 6/2652
Calculemos p(0, 1): El número de maneras de obtener una espada que no sea el as y una cualquiera de las restantes, es C(4, 0) x C( 12, 1) x C(36, 1). Luego la probabilidad pedida es p(0,1) = 864/2652
Ahora p(0,2) = C(4, 0) x C(12, 2) x C(36, 0)/ 2652 = 132/2652
Calculemos ahora p(2, 1):
La probabilidad de extraer el as de espadas y otro as cualquiera es 1/52 x 3/51 = 3/1326. Esto significa que hemos extraído 2 ases y una espada.
Por el contrario p(1, 2) significa extraer dos espadas, de las cuales una es el as de espadas. La probabilidad de hacerlo es 1/52 x 12/51 = 12/1326
p(2, 2) = 0. No se extraen tres o cuatro cartas.
Finalmente p(1,1) significa la probabilidad de extraer el as de espada y una espada que no debe ser el as de espada. La probabilidad de extraer el as de espada es 1/52. Una espada que no sea el as de espada se obtiene con probabilidad 12/51. Pero hay 12 formas diferentes de extraer una de tales cartas. Luego la probabilidad p(1,1) = (1/52) x (12/51) x 12 = 144/1326
Esto completa la distribución de probabilidad pedida, que se muestra en el siguiente cuadro:
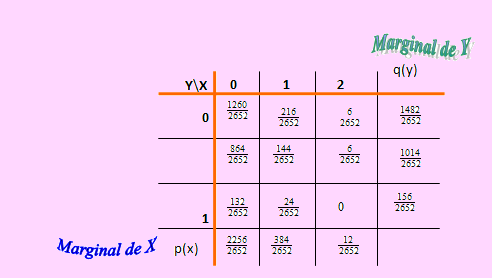
Las distribuciones marginales también se muestran en la figura anterior.
Sea A el evento definido como “El número de ases sea mayor que el número de espadas”.
Esto significa que A = {(X, Y) / X > Y }.
Según esto, P(A) = P({(1,0), (2, 0), (2, 1) } ) = 228/2656
Distribuciones condicionales
Caso discreto:
Sea (X, Y) una variable aleatoria bidimensional discreta, cuya función de probabilidad conjunta es p(xi, yj).
Sea p(xi) y q(yj) , i =1, 2, ..., n, ...; j = 1, 2, ..., m, ... , las distribuciones de probabilidad marginal de X e Y. Diremos que pX/Y(xi/Y = yj) es la función de probabilidad condicional de X, dado Y = yj, si

Ejemplo 169
Obtener las distribuciones condicionales de X, dado Y = 1 e Y, dado X = 2, del problema planteado en el Ejemplo Nº 10.
Solución
Sea (X, Y) la variable aleatoria bidimensional discreta cuya función de probabilidad conjunta es, de acuerdo al Ejemplo 10,
p(x, y) = (x2 + y2)/32, x = 0, 1, 2, 3; y = 0, 1
Para obtener la distribución de probabilidad condicional de X dado Y = 1, debemos encontrar primero la distribución marginal de Y, de ella extraemos q(y = 1).
Del mismo modo, para obtener la distribución de probabilidad condicional de Y dado X = 2, debemos encontrar primero la distribución marginal de X, de ella extraemos p(x = 2).
En consecuencia debemos encontrar las dos distribuciones marginales y luego proceder a encontrar la condicional respectiva.
Distribución Marginal de X: p(x) = (2x2 + 1) / 32, x = 0, 1, 2, 3.
Distribución Marginal de Y: p(y) = (14 + 4y2) / 32; y = 0, 1.
Distribución Condicional de X, dado Y = 1:

Ejemplo 170
Un inversionista tiene que adquirir dos paquetes de acciones de un conjunto de 5 paquetes disponibles en el momento de la apertura de la bolsa.
Antes de seleccionar el paquete a ser adquirido, realiza un concienzudo análisis de rentabilidad y si estos resultados le satisfacen, adquiere el paquete. Puesto que dicho análisis implica un alto costo, decide realizar las pruebas sólo hasta encontrar los dos paquetes que le satisfacen.
Denotemos por X el número de pruebas que debe realizarse hasta encontrar el primer paquete aceptable e Y el número de pruebas adicionales hasta encontrar el segundo aceptable.
a) Obtenga la distribución de probabilidad conjunta de (X, Y)
b) Obtenga las distribuciones marginales de X e Y
c) Obtenga la distribución condicional de X dado Y = 2 y la distribución condicional de Y dado X = 3.
Solución
Sea X la variable aleatoria definida como “El número de pruebas realizadas hasta adquirir el primer paquete de acciones”. Igualmente sea Y, “El número de pruebas adicionales hasta adquirir el segundo paquete de acciones”.
Según esto, los valores que tomen las variables serán: X: 1, 2, 3, 4; Y: 1, 2, 3, 4.
Nos explicamos: Si el primer paquete le satisface al inversionista, lo adquiere, de manera que X = 1, esto implica que el segundo paquete puede adquirirse después de la primera, segunda, tercera o cuarta prueba, lo que significa que Y puede tomar valores 1, 2, 3 ó 4.
El primer paquete debe ser adquirido en la primera, segunda, tercera o cuarta prueba, necesariamente.
Sea A el evento que representa la opción de “Adquirir el paquete” y B, el evento “Adquirir el segundo paquete”. De acuerdo a esto, p(1, 1) = P(X = 1, Y = 1) representa la probabilidad de que el primer paquete se adquiera en la primera prueba y el segundo, en la siguiente prueba(una prueba adicional). Usando A y B, tenemos p(1, 1) = P({AB}) = (2/5)(1/4) = 0.1.
Del mismo modo, p(1, 2) = P(X = 1, Y = 2 ) = P({AB’B}) = (2/5)(3/4)(1/3) = 0.1 Es decir, la probabilidad de que se adquiera el primero en la primera prueba y el segundo en la tercera es 0.1.
p(1, 3) = P({AB’B’B}) =(2/5)(3/4)(2/3)(1/2) = 0.1
p(1, 4) = P({AB’B’B’B}) = (2/5)(3/4)(2/3)(1/2)(1/1) = 0.1
p(2, 4) = P({A’AB’B’B’B}) = 0 este es un evento imposible
a) En el siguiente cuadro se muestra la distribución de probabilidad conjunta de X e Y
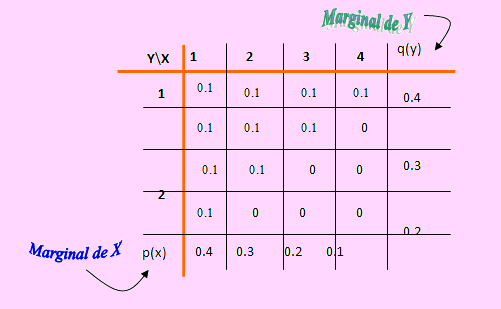
b) En el mismo cuadro de distribución hemos sumado por fila para encontrar la distribución marginal de Y, y luego hemos sumado por columna para encontrar la distribución marginal de X.
De manera que, la distribución marginal de X es

c) Distribución condicional de X dado Y = 2:
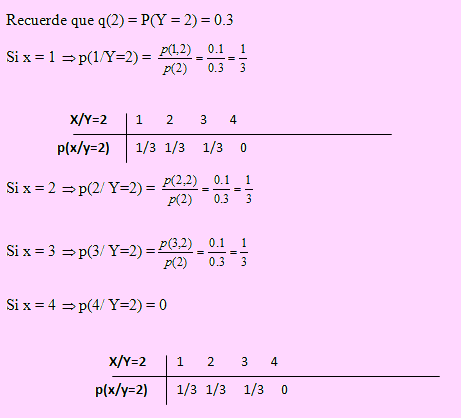
La marginal de Y, dado X = 3 :
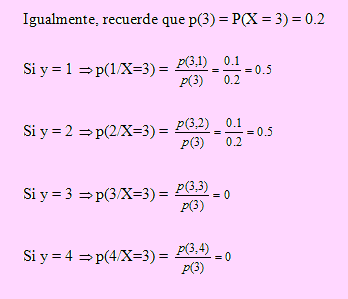
Esperanza condicional
Caso discreto:
Sea (X, Y) una variable aleatoria bidimensional discreta con p(xi, yj) , i = 1, 2, ..., n, ...; j = 1, 2, ..., m, ... su función de probabilidad conjunta. Sea p(xi) y q(yj) las funciones de distribución marginal de X e Y, respectivamente.

Ejemplo 171
Sea (X, Y) una variable aleatoria bidimensional discreta cuya función de probabilidad conjunta es
p(x, y) = (2x + y)/63; x = 1, 2, 3; y = 2, 3, 4.
Encuentre las esperanzas condicionales E[X/Y] y E[Y/X], para todos los valores de X e Y.
Solución
Como para E[X/Y] se requiere la marginal de Y y la probabilidad condicional de X, dado Y, así como para E[Y/X] se requiere la marginal de X y luego la probabilidad condicional de Y, dado X, procedamos de manera ordenada:
Distribución Marginal de X:
p(x) = (6x + 9)/63; x = 1, 2, 3.
Distribución Marginal de Y:
p(y) = (12 + 3y)/63; y = 2, 3, 4.
Distribución condicional de X, dado Y:

Con toda esta información

Ejemplo 172
Se sabe que la probabilidad de que llueva en un día cualquiera es 10% en una determinada ciudad.
Si se define a X como el número de días que llueve en los cuatro primeros días de la semana y a Y como el número de días que llueve en los cuatro últimos días de la semana,
a) Determine la distribución de probabilidad conjunta de X e Y
b) Encuentre la probabilidad P(X < 2 / Y > 2)
c) Encuentre la probabilidad de que llueva exactamente en 4 días de la semana
Solución
Sea X: “Número de días que llueve entre el Lunes, Martes, Miércoles, Jueves” ,
del mismo modo, sea Y: “Número de días que llueve entre el Jueves, Viernes, Sábado, Domingo”.
De acuerdo a esto, X: 0, 1, 2, 3, 4 y también, Y: 0, 1, 2, 3, 4.
La probabilidad de que llueva en un día cualquiera de la semana es 0.10. Si sólo se definiera a X como el número de días que llueve en la semana, entonces estaríamos frente a una distribución binomial de parámetros n = 7 y p = 0.10.
Sin embargo, no estamos muy alejados de ella pues por la manera cómo se define a X e Y, daría la impresión de estar frente a una distribución “binomial conjunta”, excepto por lo del Jueves que está siendo incluido tanto en X como en Y. Por ello encontraremos las probabilidades individuales y luego armaremos el cuadro de distribución para, a partir de ella encontrar resolver la(s) pregunta(s).
a) p(0,0) = P(X = 0, Y = 0) significa que no debe llover los 4 primeros días, ni menos los últimos 4 días.
Esto es, p(0, 0) = C(7, 0)(0.1)0(0.9)7 = 0.97.
p(0, 1) = P(X = 0, Y = 1) significa que no debe llover de Lunes a Jueves, pero sí Viernes, Sábado o Domingo; esto es, p(0, 1) = 0.94 . C(3, 1)(0.1)0.92 = 3(0.1)(0.9)6
p(1, 0) = 3(0.1)(0.9)2(0.9)4 ; es decir, p(0, 1) = p(1, 0).
p(0, 2) = p(0, 2) = C(3, 2)(0.1)2(0.9)5 = 3(0.1)2(0.9)5.
p(0, 3) = p(3, 0) = C(3, 3)(0.1)3(0.9)4 = (0.1)3(0.9)4. p(0, 4) = p(4, 0) = 0.
Imposible. No debe llover el jueves y debe llover, también, el jueves.
p(1,1)=P(Llueve Jueves)+P(No llueve Jueves) = (0.1)(0.9)6 + C(3,1)(0.1)(0.9)3C(3,1)(0.1)0.92
p(2, 2) = C(3,2)(0.1)2(0.9)2C(3,2)(0.1)2(0.9) + C(3, 2)(0.1)2(0.9)2C(3,2)(0.1)(0.9)2
p(3, 3) = (0.1)6(0.9) + 9(0.1)3(0.9)(0.1)2(0.9)
p(4, 4) = (0.1)4(0.9)0(0.1)3(0.9)0 = (0.1)7
Dejamos para el lector el cálculo de las siguientes probabilidades individuales.
La distribución de probabilidades se muestra en la siguiente tabla.
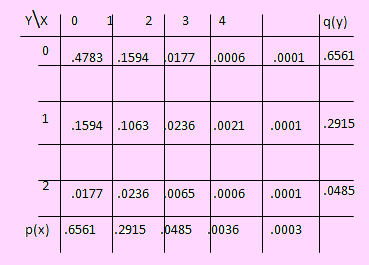
b) P(X < 2 / Y > 2) = P(X < 2, Y > 2) / P(Y > 2) = 0.0029 / 0.0039 = 29/39
Sea A el evento: “Que exactamente llueva 4 días en la semana”. Si definimos a la variable Z como “Número de veces que llueve en la semana” entonces Z → B(n = 7, p = 0.10). Por ello, P(A) = P(Z = 4 ) = C(7,4)0.40.93
Ejemplo 173
Si la distribución de probabilidad conjunta de (X, Y) viene dada por la siguiente tabla:
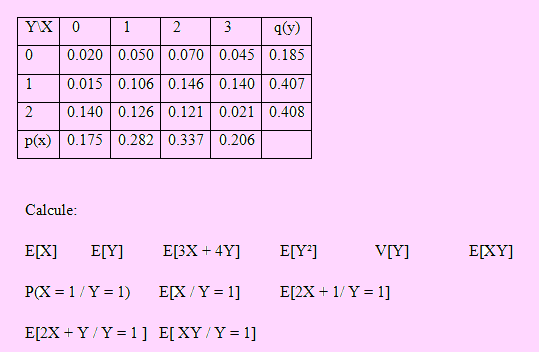
Solución
En la tabla conjunta ya hemos calculado las distribuciones marginales de X e Y.
E[X] = 0(.175)+1(.282)+2(.337)+3(.206) = 1.574
E[Y] = 0(.185)+1(.407)+2(.408) = 1.223
Sea Z = 3X + 4Y. Si X , Y = 0, 1, 2, 3, 4 entonces Z = 0, 3, 4, 6, 7, 8, 9, 10, 13, 14; con lo cual su distribución será

Luego E[Z] = 0(.02) + 3(.05) + 4(.015) + ... + 4(.121) + 17(.021) = 9.614
E[Y²] = 0²(.185) + 1²(.407) + 2²(.408) = 2.039
V[Y] = E[Y²] – (E[Y])² = 2.039 – 1.223² = 0.543271
Antes de evaluar E[XY], encontremos la distribución de XY. Para ello, sea Z = XY. Los valores que toma Z son:
0 = {(0,0), (1, 0), (2, 0), (3, 0), (0, 1), (0, 2)},
1 = {(1, 1) } 2 = {(1, 2), (2, 1) } 3 = {(3, 1)},
4 = {(2, 2) } 6 = {(3, 2) }
Luego su distribución es
| 0 |
1 |
2 |
3 |
4 |
6 |
| 0.340 |
0.106 |
0.272 |
0.140 |
.121 |
0.021 |
De acuerdo a esto, E[XY] = E[Z] = 1.680
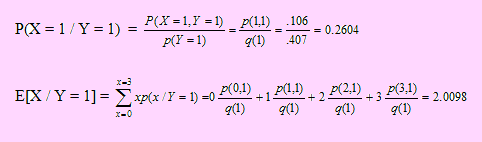
E[2X + 1 / Y = 1 ]
Aplicando propiedades, E[2X + 1/Y= 1]= 2 E[X / Y = 1] + 1 = 2(2.0098) + 1= 5.0196
E[2X + Y / Y = 1]. Como ya ha ocurrido el evento { Y = 1 } entonces ya se conoce el valor de Y, por ello E[2X + Y / Y = 1] = E[2X + 1 / Y = 1] = 5.0196
Igualmente, E[XY / Y = 1 ] = E[X(1) / Y = 1] = E[X / Y = 1 ] = 2.0098
Variables aleatorias independientes
Caso discreto:
Sea (X1, X2, ..., Xn) una variable aleatoria n-dimensional discreta donde p(x1, x2, ..., xn) es su función de probabilidad conjunta y p(x1), p(x2), ... p(xn) sus funciones de distribución marginal respectivas. Diremos que X11, X2, ..., Xn son variables aleatorias independientes si p(x1, x2, ..., xn) = p(x1,)p( x2,) ...,p(xn)
Caso continuo:
Si (X1, X2, ..., Xn) es una variable aleatoria n-dimensional continua conf su distribución de probabilidad conjunta y g(x1), g(x2), ..., g(xn) son sus funciones de distribución marginales respectivas. Diremos que X1, X2, ..., Xnson variables aleatorias independientes si su función de densidad conjunta es el producto de sus respectivas distribuciones marginales. Esto quiere decir que f(x1, x2, ..., xn) = g(x1,)g( x2,) ...,g( xn)
Ejemplo 174
Dada la distribución de probabilidad conjunta de (X, Y), determine si X e Y son independientes o no.
| Y \ X |
0 |
1 |
2 |
q(y) |
| 0 |
0.2 |
0.1 |
0.1 |
0.40 |
| 1 |
0.1 |
0.3 |
0.2 |
0.6 |
| p(x) |
0.3 |
0.4 |
0.3 |
|
Aplicando la definición, tenemos
Según la distribución conjunta p(0, 0) = P(X = 0 , Y= 0) = 0.2 y
Del mismo modo, P(X = 0) . P(Y= 0) = 0.3 x 0.4 = 0.12
Como existe un (x, y) en la cual no se cumple la definición, entonces X e Y no son variables aleatorias independientes.
Ejemplo 175
Dada la distribución de probabilidad conjunta de (X, Y), determine si X e Y son independientes o no.
| Y \ X |
0 |
1 |
2 |
q(y) |
| 0 |
0.21 |
0.14 |
0.35 |
0.70 |
| 1 |
0.09 |
0.06 |
0.15 |
0.30 |
| p(x) |
0.30 |
0.20 |
0.50 |
|
Aplicando la definición, tenemos
Si p(0, 0) = 0.21 y P(X ≤ 0) . P(Y ≤ 0) = 0.3 x 0.7 = 0.21 ⇒ Se cumple
Si p(1, 0) = 0.14 y P(X = 1) . P(Y= 0) = 0.2 x 0.7 = 0.14 ⇒ Se cumple
Si p(2, 0) = 0.35 y P(X = 2) . P(Y= 0) = 0.5 x 0.7 = 0.35 ⇒ Se cumple
Si p(0, 1) = 0.09 y P(X = 0) . P(Y = 1) = 0.3 x 0.3 = 0.09 ⇒ Se cumple
Si p(1, 1) = 0.06 y P(X = 1) . P(Y= 1) = 0.2 x 0.3 = 0.06 ⇒ Se cumple
Si p(2, 1) = 0.15 y P(X = 2) . P(Y= 1) = 0.15 ⇒ Se cumple
Por tanto, como para todo (x, y) se cumple que p(x, y) = P(X = x, Y = y) entonces X e Y son variables aleatorias independientes.
Covarianza de dos variables
Sean X e Y dos variables aleatorias con μX = E[X], μY = E[Y], del mismo modo, σ2 = V[X] y σ2 = V[Y]. Diremos que Cov(X, Y) es la covarianza de X e Y, la que será definida como
Cov(X, Y) = E[(X - μX)(Y - μY)]
Teorema
Cov(X, Y) = E(XY) - E(X) E(Y)
En efecto,
Cov(X,Y) = E[XY - XμY- μXY + μX μY]
= E(XY)-E(X) μY - μXE(Y) + μXμY
=E(XY)- μX μY
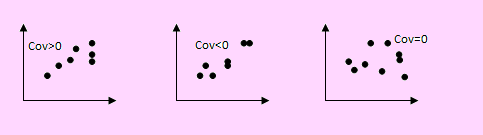
La covarianza permite saber si existe alguna relación entre las dos variables. En las siguientes figuras hemos trazado la gráfica de la venta del pollo y su precio.
En la primera figura tenemos la demanda (X) vs el precio (Y)
En la segunda, la oferta (X) vs el precio (Y)
En la tercera, en la tercera gráfica, X puede ser considerada como la demanda u oferta del pollo mientras que Y será el precio.
En la primera figura podemos apreciar que, cuando la demanda aumenta, también aumenta el precio mientras que en la segunda, cuando aumenta la oferta del pollo, el precio del mismo disminuye.
En la tercera figura cuando la variable X aumenta, nada puede decirse de Y pues ésta aumenta o disminuye, independientemente de X.
En la primera y segunda figura existe relación entre la demanda u oferta del pollo y su precio. En el primer caso hay una relación directa positiva; en la segunda existe una relación inversa negativa. En la tercera figura podemos apreciar que las dos variables (X e Y) son independientes.
Ejemplo 176
El administrador de una playa pública desea realizar un estudio sobre los ingresos que tiene en cada temporada veraniega. Estos ingresos son de preocupación ya que en cada nuevo verano se van reduciendo. Sin embargo sospecha también que esto podría deberse al incremento de la gasolina que impide que los usuarios tengan un gasto adicional. ¿Se podría decir que sus ingresos dependen del precio de la gasolina? Los datos se encuentran en el siguiente cuadro:
| Mes |
Ingreso |
Gasolina ($/litro) |
| Enero |
290 |
0.40 |
| Febrero |
200 |
0.34 |
| Marzo |
250 |
0.31 |
| Abril |
490 |
0.25 |
| Mayo |
410 |
0.25 |
| Junio |
360 |
0.34 |
| Julio |
300 |
0.27 |
| Agosto |
150 |
0.39 |
| Setiembre |
200 |
0.33 |
| Octubre |
100 |
0.35 |
Solución
Obtenga la covarianza de los ingresos y el precio de la gasolina.
Sea X la variable Ingresos y Y la variable Gasolina.
Ingrese los datos a una hoja del Excel, como se muestra en la siguiente gráfica:
Cómo calcular la covarianza en Excel:
Podemos hacerlo de dos formas:
Primera forma:
Usando la función: =Covar(Mariz1,Matriz2)
Donde Matriz1 y Matriz2 representan los rangos de la primera y segunda variable, respectivamente.
En este ejemplo, En F3 digitemos: =Covar(B1:B11,C1:C11)
Lo que nos dará como resultado: -3.885.
Segunda forma:
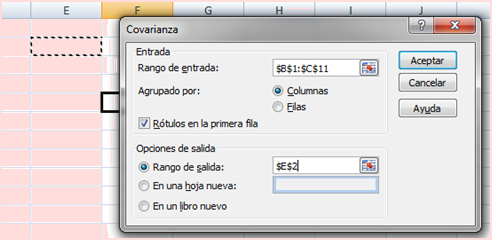
Usando la herramienta Covarianza del grupo [Análisis de datos] de la ficha [Datos]
En la ventana que se obtiene a continuación, se debe ingresar los datos como se muestra en la siguiente imagen:
Al hacer clic en obtendremos los siguientes resultados a partir de E2:
| |
Ingreso |
Gasolina |
| Ingreso |
1305 |
|
| Gasolina |
-3.885 |
0.002541 |
Esta herramienta del Excel, además de la covarianza = -3.885, nos proporciona la varianza poblacional de cada una de las variables, las que se encuentran en la diagonal.
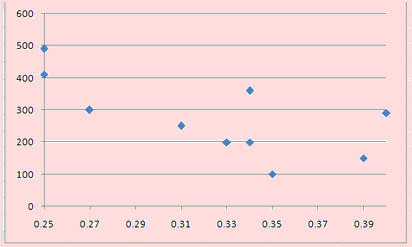
Antes de interpretar la covarianza, construyamos el diagrama de dispersión de estas dos variables. Dicha gráfica se muestra en la figura 4.49 En ella podemos apreciar que, a medida que el precio de la gasolina se incrementa, los ingresos se reducen. Interpretación de la covarianza
Tomando en cuenta lo dicho anteriormente, podemos concluir en lo siguiente:
La covarianza permite saber si dos variables están relacionadas o no.
Si Cov(X, Y) > 0 se dirá que la relación existente es directa; es decir, cuando una variable aumenta, la otra variable también aumenta.
Si Cov(X, Y) < 0 se dirá que la relación existente es inversa; es decir, cuando una variable aumenta, la otra variable se reduce.
Si Cov(X,Y) = 0 diremos que no existe relación entre las dos variables, o lo que es lo mismo, las dos variables son independientes.
Coeficiente de correlación
Sean X e Y dos variables aleatorias con μX = E[X], μY = E[Y], del mismo modo, σ2 = V[X] y σ2 = V[Y]. Diremos que ρ es el coeficiente de correlación entre X e Y, la que estará definido como
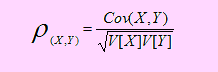
Propiedades
1. Si las variables aleatorias X e Y son independientes entonces ρ = 0
2. Si X e Y son variables aleatorias independientes entonces Cov(X, Y) = 0
3. Si Z = aX ± bY ⇒ V[aX ± bY] = a2 V[X] + b2 V[Y] ± 2 a b Cov(X, Y)
4. Si ρ es el coeficiente de correlación entre X e Y entonces -1 ≤ ρ(X, Y) ≤ 1.
Observación:
1. Si ρ = +1, diremos que entre X e Y existe una correlación perfecta positiva.
2. Si ρ = -1, diremos que entre X e Y existe una correlación perfecta negativa.
3. Para valores de ρ, cercanos a ± ½ diremos que existe una correlación moderadamente perfecta positiva o negativa, respectivamente.
4. El hecho de que ρ = ± 1, implica que existe una relación de una variable respecto de la otra. Por costumbre y porque coincide con el tratamiento que hemos hecho de X e Y, supondremos que, bajo las circunstancias en que ρ → ± 1, es posible definir a Y como una combinación lineal de X; es decir Y = A X + B, donde A y B son números reales con A > 0 cuando ρ = +1 y A < 0 cuando ρ = - 1.
Esta última observación da origen a un teorema, que lo enunciaremos sin demostración.
Ejemplo 177
Dada la función de probabilidad conjunta de X e Y
| Y \ X |
0 |
1 |
| 0 |
0.13 |
0.13 |
| 1 |
0.25 |
0.13 |
| 2 |
0.25 |
0.13 |
Hallar:
a) Cov(X, Y)
b) V[X], V[Y]
c) ρ(X, Y)
d) V[X + Y]
e) ρ(2X, 3Y + 4)
Solución

E[X] = 0(5/8) + 1(3/8) = 3/8
E[Y] = 0(2/8) + 1(3/8) + 2(3/8) = 9/8
E[XY] = 0(6/8) + 1(1/8) + 2(1/8) = 3/8

Ejemplo 178
Un puerto tiene capacidad para acomodar 4 naves de cierto tipo durante la noche.
Las tarifas del puerto producen una utilidad de $ 1,000 por nave atracada. Sea X la variable aleatoria que representa el número de naves buscando atracadero por noche, donde p(X = k) = 1/6, para k = 1, 2, 3, 4, 5 es la función de probabilidad de X.
Un segundo puerto está disponible para manejar el exceso de naves, si existen. Sea Y representa el número de naves buscando atracadero en el segundo puerto (lo cual sólo ocurrirá si el primer puerto está lleno).
Calcular
a) La distribución de probabilidad conjunta de X e Y
b) Las distribuciones marginales de X e Y
c) La distribución condicional de Y, dado X = 4
d) ¿Son independientes las variables X e Y?
e) V[X], V[Y]
f) La covarianza de X e Y
g) El coeficiente de correlación de X e Y
Solución
Sea X la variable que representa “Numero de naves que obtienen espacio en el primer puerto”
Sea Y la variable que representa “Número de naves que van a un segundo puerto”
Nota:
Observe que el número de naves que puede aceptar el primer puerto es hasta 4. Por lo que diremos que X = 0, 1, 2, 3, 4. Pero como k = 1, 2, 3, 4, 5, entonces P(X >4) = 2/6.
Toda vez que X 4, no hay naves que vayan al segundo puerto, por lo que Y = 0
Toda vez que X > 4, las restantes naves van al segundo puerto, por lo que Y = 1, 2,...
Pero por noche sólo son 5 naves que buscan atracadero. Esto quiere decir que tomará valores entre 0 y 1. Por tanto X = 0, 1, 2, 3, 4; mientras que Y = 0, 1.
a) La distribución de probabilidad conjunta de X e Y es
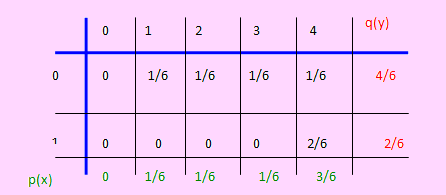
b) Las distribuciones marginales de X e Y se muestran en el cuadro anterior
c) p(y / X = 4) = p(4,y) / P/X = 4) = (p(4,0) + p(4, 1) ) / p(4) = 1.
d) Puesto que p(xi)q(yj) es diferente a p(xi,yj) para algú n i = 1, 2, 3, 4, 5, ó j = 1, 2 entonces X e Y no son variables aleatorias independientes.
e) Para encontrar las varianzas:
E[X] = 0 + 1/6 + 2/6 + 3/6 + 12/6 = 3
E[Y] = 0 + 2/6 = 2/6
E[X2] = 0 + 1/6 + 4/6 + 9/6 + 48/6 = 62/6
E[Y2] = 0 + 2/6 = 2/6
Luego V[X] = 4/3 ; igualmente V[Y] = 2/9
f) Antes de encontrar la covarianza debemos hallar E[XY].
E[XY] = 0 + 0 + 0 + 0 + 8/6 = 4/3
Cov(X, Y) = 4/3 – (3)(2/6) = 1/3
g) Cálculo del coeficiente de correlación:
ρ(X, Y) = cov(X, Y) / √ (V(X)V(Y)) = (1/3) / &raidc; (8/27) = 0.6124. Era de esperarse este resultado.
Ejemplo 179
Construya una macro que permita realizar todos los cálculos relativos a una variable aleatoria bidimensional discreta a partir de la distribución de probabilidad conjunta ingresada en una hoja del Excel. La macro debe ser capaz de recibir una tabla de cualquier tamaño y realizar todos los cálculos como las distribuciones marginales, las esperanzas, esperanzas condicionales, varianzas, covarianza y el coeficiente de correlación.La siguiente imagen corresponde a un segmento de la hoja que se debe diseñar. Toda la información obtenida a partir de la fila 8 debe ser obtenida mediante la macro.
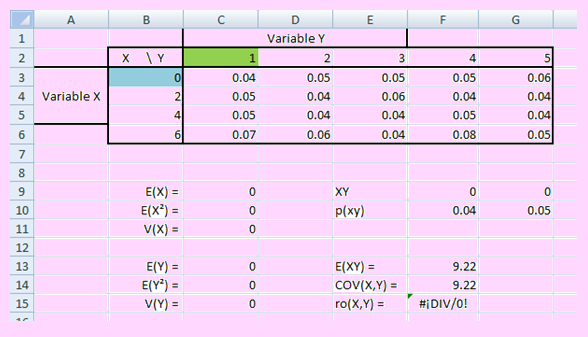
La siguiente es la macro que resuelve lo pedido:
Dim nx, ny, mx, my As Integer
Sub DistrBid()
'Hoja = InputBox("Nombre de la hoja")
'Sheets(Hoja).Select
Range("C2").Select
ny = Selection.End(xlToRight).Column
Range("B3").Select
nx = Selection.End(xlDown).Row
Cells(2, ny + 1) = "Marginal de X"
Cells(2, ny + 1).ColumnWidth = 14
Cells(nx + 1, 2) = "Marginal de Y"
mx = nx - 2
my = ny - 2
For j = 3 To nx
Cells(j, ny + 1).Select
Cells(j, ny + 1) = "=Sum(RC3:RC[-1])"
Next
For j = 3 To ny
Cells(nx + 1, j).Select
Cells(nx + 1, j) = "=Sum(R3C:R[-1]C)"
Next
ValEsp
ValEspXY
End Sub
Sub ValEsp()
Cells(nx + 3, 2) = "E(X) = "
Cells(nx + 7, 2) = "E(Y) = "
Cells(nx + 4, 2) = "E(X²) = "
Cells(nx + 8, 2) = "E(Y²) = "
Cells(nx + 5, 2) = "V(X) = "
Cells(nx + 9, 2) = "V(Y) = "
ActiveWorkbook.Names("Rx").Delete
ActiveWorkbook.Names("Ry").Delete
ActiveWorkbook.Names("Rpy").Delete
ActiveWorkbook.Names("Rpx").Delete
ActiveWorkbook.Names("Rxy").Delete
ActiveWorkbook.Names("Rpxy").Delete
Range(Cells(2, 3), Cells(2, ny)).Name = "Ry"
Range(Cells(nx + 1, 3), Cells(nx + 1, ny)).Name = "Rpy"
Range(Cells(3, 2), Cells(nx, 2)).Name = "Rx"
Range(Cells(3, ny + 1), Cells(nx, ny + 1)).Name = "Rpx"
Cells(nx + 3, 3).Select
ActiveCell = "=SUMPRODUCT(Rx,Rpx)"
ActiveCell.Name = "Ex"
Cells(nx + 4, 3).Select
ActiveCell = "=SUMPRODUCT(Rx,Rx,Rpx)"
Cells(nx + 5, 3).Select
ActiveCell = "=R[-1]C-R[-2]C^2"
ActiveCell.Name = "Vx"
Cells(nx + 7, 3).Select
ActiveCell = "=SUMPRODUCT(Ry,Rpy)"
ActiveCell.Name = "Ey"
Cells(nx + 8, 3).Select
ActiveCell = "=SUMPRODUCT(Ry,Ry,Rpy)"
Cells(nx + 9, 3).Select
ActiveCell = "=R[-1]C-R[-2]C^2"
ActiveCell.Name = "Vy"
End Sub
Sub ValEspXY()
Cells(nx + 3, 5) = "XY "
Cells(nx + 4, 5) = "p(xy)"
k = 5
For i = 3 To nx
For j = 3 To ny
k = k + 1
Cells(nx + 3, k) = Cells(i, 2) * Cells(2, j)
Cells(nx + 4, k) = Cells(i, j)
Next
Next
Range(Cells(nx + 3, 6), Cells(nx + 3, 5 + mx * my)).Name = "Rxy"
Range(Cells(nx + 4, 6), Cells(nx + 4, 5 + mx * my)).Name = "Rpxy"
Cells(nx + 7, 5) = "E(XY) = "
Cells(nx + 7, 6) = "=SumProduct(Rxy,Rpxy)"
Cells(nx + 7, 6).Name = "Exy"
Cells(nx + 8, 5) = "COV(X,Y) = "
Cells(nx + 9, 5) = "ro(X,Y) = "
Cells(nx + 8, 6) = "=Exy-Ex*Ey"
Cells(nx + 8, 6).Name = "Cov"
Cells(nx + 9, 6) = "=Cov/sqrt(Vx*Vy)"
'Cells(nx + 8, 6) = Cells(nx + 7, 6) - Cells(nx + 3, 3) * Cells(nx + 7, 3)
'Cells(nx + 9, 6) = Cells(nx + 8, 6) / Sqr(Cells(nx + 5, 3) * Cells(nx + 9, 3))
End Sub
Sub Clear()
Range(Cells(2, ny + 1), Cells(nx + 1, ny + 1)).ClearContents
Range(Cells(nx + 1, 2), Cells(nx + 1, ny + 1)).ClearContents
End Sub
4.15 PROBLEMAS PROPUESTOS
1. La distribución de probabilidad conjunta de X e Y se define como
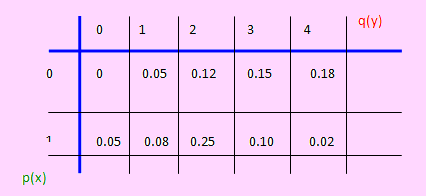
(X: 0, 1, 2, 3, 4 Y: 0, 1 )
a) Encuentre las distribuciones marginales de X e Y b) Calcular p(x / Y = 1)
c) Calcular p(y / X = 3)
2. Dos firmas financieras de gran prestigio en el mercado local controlan el 50 y 30% del mercado, respectivamente. Si se escoge al azar una muestra de 2 clientes para una investigación, ¿cuál es la distribución de probabilidad conjunta del número de compradores que favorecen a cada firma de la muestra? Calcular E[X], E[Y], E[X + Y] y E[XY].
3. Considere las variables aleatorias independientes X e Y, las cuales sólo pueden tomar los valores –1, 0, 1. Suponga que p(-1) = P(X = -1) = P(X = 1) = 1/4 . Por otro lado, suponga que P( Y = -1 ) = P(Y = 0 ) = 1/3.
a) Calcular E[X] y E[Y]
b) Si T = 3X + 4Y, evalúe E[T]
4. Suponga que se extraen aleatoriamente dos cartas de un naipe de 52 cartas. Sea X el número de diamantes e Y el número de ases obtenidos. Encuentre las distribuciones marginales de X e Y.
5. En una población muy grande de familias con 3 hijos consideramos las variables aleatorias:
X: “Número de hijos varones en la familia”
Y: “Número de rachas en el sexo de los hijos”.
a) Si cada hijo tiene la misma probabilidad de ser varón que de ser mujer, hallar la función de distribución de probabilidad de X e Y.
b) Hallar las distribuciones marginales de X e Y. Son X e Y independientes?
c) Obtener las distribuciones condicionales de Y sabiendo que X = 1
d) Calcular el valor esperado de Y sabiendo que X = 1
6. En un estudio sobre rotación del personal policial en una determinada población se encontró que el número de cambios que experimentaba un personal subalterno era una variable aleatoria, X y que en cada cambio dicho personal tenía un ingreso salarial, definido por la variable aleatoria Y. Si la distribución de probabilidad conjunta de estas dos variables se da en el siguiente cuadro
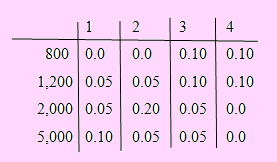
a) Calcular P(X = 2)
b) P(X = 2 / Y = 1200)
c) Son independientes X e Y?
d) Hallar V[X], V[Y]
e) Hallar V[X + Y]
f) Hallar V[X Y]
Siguiente sesión.