Distribución Uniforme
Sea X una variable aleatoria continua definida sobre el intervalo (a, b). Diremos que X es una variable aleatoria que tiene Distribución Uniforme sobre el intervalo (a, b) y lo denotaremos por XU(a,b) y su función de densidad de probabilidad será
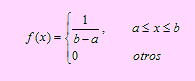
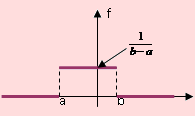
1. La figura 4.25 muestra la gráfica de la distribución uniforme
2. Su distribución acumulada
La función de distribución acumulada F de una variable que se distribuye uniformemente es
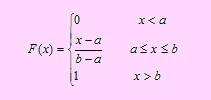
El programa Excel no dispone de alguna herramienta para la distribución Uniforme; sin embargo podemos hacer uso de la distribución acumulada para evaluar probabilidades referidas a la distribución uniforme.
Veamos:
Si X → U(a, b) entonces P(X < k) = P(X ≤ k) = (k - a) / (b - a)
Teorema
Si X es una variable aleatoria que se distribuye uniformemente sobre el intervalo (a, b) entonces
μ = (a + b) / 2.
σ2 = (b - a)2 / 12
Ejemplo 121
Sea X una variable aleatoria que se distribuye uniformemente sobre el intervalo (10, 20). Diga si son verdaderas o falsas las siguientes proposiciones:
El espacio rango de X es (0, +∞ )
El valor esperado de X es 15
La desviación estándar de X es 15
El valor esperado de X² es mayor que 15
El 80% de los valores de X son superiores a 18
Solución
De acuerdo a la definición si X tiene distribución uniforme sobre (10, 20) entonces su función de densidad viene dada por f(x) = 1 / (b-a), a ≤ x ≤ b; como tal, su espacio rango es el conjunto RX = {x / 10 ≤ x ≤ 20 }.
Por lo que la proposición es Falsa.
Puesto que E[X] = entonces E[X] = 15.
La proposición es Verdadera.
Sabemos que V[X] =(b-a)2 . La desviación estándar σX = 2.887.
Luego la proposición es Falsa.
E[X²] es la integral de 10 hasta 20 de x2 e igual a 700/3. Esto implica que E[X²] > 15.
Luego es Verdadero
“El 80% de los valores de X son superiores a 18” se interpreta matemáticamente como que P(X > 18 ) = 0.80.
Veamos si esto es cierto:
P(X > 18) = 1 – F(18) = 1 - (18-10) / 10 = 0.2. La proposición es Falsa.
Ejemplo 122
Sea X una variable aleatoria continua con distribución uniforme sobre el intervalo (-2, 2). Calcular:
a) P(X < 3/2 ) P(-1 < X ≤ 1)
b) P( | X | > 3/2 ) P( | X - μ | ≤ 1)
c) P(μ - 2σ≤ X ≤ μ + 2σ )
Solución
Como X es una variable aleatoria con distribución uniforme sobre (-2, 2), entonces su función de densidad viene dada por
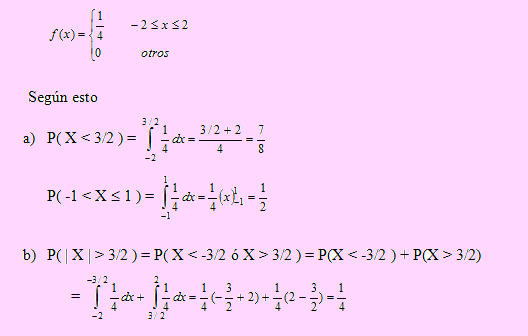
Para hallar P( | X - μ | ≤ 1) debemos tener el valor de μ.
Como μ = E[X] = (a + b) / 2 , entonces μ = 0
Luego P( | X - μ | ≤ 1) = P( | X - 0 | ≤ 1) = P( | X | ≤ 1 ) = P( -1 < X ≤ 1 ) = 1/2
c) Obtención de la desviación estándar, σ:
Como σ2 = V[X] = (b - a)2, entonces σ = √ (16/12) = 1.155
Con lo cual P(μ - 2σ ≤ X ≤ μ + 2σ ) = P(0 – 2(1.155) ≤ X ≤ 0 + 2(1.155)) = 1 ya que
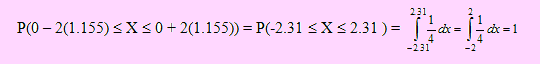
Ejemplo 123
Sea X una variable aleatoria con distribución uniforme en (-a, a) , donde a > 0. Cada vez que sea posible, determinar a, de manera que se cumpla lo siguiente:
a) P( | X | > 1 ) = P( | X | < 1 )
b) P( X > 1 ) = 1/3
c) P(X < 1/2 ) = 0.7
Solución
a) Si P( | X | > 1 ) = P( | X | < 1 ) entonces 1 - P( | X | ≤ 1 ) = P( | X | < 1 ).
Simplificando y “despejando la incógnita”, tenemos P( | X | ≤ 1 ) = 0.5. Esto significa que
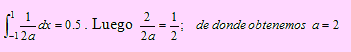
b) Si P( X> 1 ) = 1/3 entonces P(X ≤ 1) = 2/3. Como por otro lado sabemos que F(x) = (x-a) / (b-a), entonces (1+a)/2a = 2/3 de donde a = 3.
c) P(X < 1/2) = 0.7 implica que F(1/2) = 0.7, de donde a = 10/8 = 1.25
Ejemplo 124
Isabel Ventura es una eficiente y preocupada gerente de operaciones de una aerolínea local. Sus investigaciones sobre el servicio de vuelos en la ruta Lima - Miami – Lima indican que se ha incrementado considerablemente debido a una fuerte promoción al turismo.
Puesto que este servicio depende de la ruta Lima – Cuzco, que también la cubre, el incremento observado puede verse afectado si el tiempo de vuelo entre Lima y Cuzco se incrementa.
Ella sabe que el tiempo de vuelo en esta ruta sigue una distribución uniforme con un promedio de 1.5 horas. Sabe además que la diferencia entre el mayor y menor tiempo que puede tardar un vuelo en esta ruta, es de 20 minutos. En la idea de mejorar sus servicios
a) ¿Qué porcentaje de vuelos tardará entre 84 y 96 minutos?
b) Si sólo el 5% de vuelos llega retrasado en la ruta nacional, ¿cuál es el tiempo máximo para que un vuelo no llegue retrasado?
Solución
Sea X la variable aleatoria definida como “El tiempo que tarda un vuelo entre Lima y Cuzco”.
Puesto que X tiene distribución uniforme, supondremos que el intervalo sobre el cual está definida su función de distribución f , es (a, b); valores que debemos determinar ante todo.
Como el promedio del tiempo de vuelo es 1.5 horas, entonces (a+b) / 2 = 3 / 2, de donde a+b=180, expresado en minutos.
Por otro lado, se sabe que b – a = 20 minutos.
Recordando nuestros viejos métodos de solución de sistemas de ecuaciones encontramos a = 80 y b = 100, por lo que la función de densidad de X es f(x) = 1/20 con 80 ≤ X ≤ 100. Ahora resolvamos las preguntas.
a) Usando la función de distribución acumulada de X, P(84 ≤ X ≤ 96 ) = (96 - 84) / 20 = 0.6
b) Un vuelo no llegará retrasado si su tiempo de vuelo, X es menor que un valor, digamos K. Esto ocurre con la probabilidad P( X< K) y como se desea que esto sea sólo el 5%, entonces P( X < K ) = 0.05, de donde (k-80)/20 = 0.05. Por tanto, el máximo valor de K será igual a 81.
Ejemplo 125
La Agente de corretajes “ISA” recibe de sus clientes un pago fijo de $ 1200 más una comisión del 8% sobre el beneficio que obtiene el cliente en cada transacción realizada por la agencia. Si este beneficio varía por lo general entre $ 10,000 y $ 12,000.
a) ¿Cuánto espera obtener de utilidad la agente ISA?
b) ¿Cuál es la probabilidad de que su utilidad supere los $ 2,100?
Solución
Sea X la variable aleatoria que representa “El beneficio obtenido por el cliente(en unidades de 10,000)”. Puesto que X se distribuye uniformemente entre 1 y 1.2 entonces su función de densidad viene dada por

Definamos también a Y como “La utilidad de la agente ISA”. Según el problema Y = 1200 + 0.08X.
a) E[Y] = E[1200 + 0.08X] = 1200 + 0.08E[X]
Como X tiene distribución uniforme entonces E[X] = 1.1 Luego E[Y] = 1200 + 0.08*1.1x10000 = 2080.
La agencia “ISA” espera obtener una utilidad de $ 2080.
b) Debemos encontrar P( Y > 2100). Recordemos que esta probabilidad podemos hallarla usando la función de distribución de Y, pero como esta no es conocida, y no deseamos obtenerla, usaremos el procedimiento acostumbrado:
Reemplazar la definición de Y y despejando X, resolveremos la probabilidad para X, ya que conocemos la función de distribución de X.
En efecto
P(Y > 2100 ) = P( 1200 + 0.08X > 2100) = P(0.08X > 900).
Como X está en unidades de diez mil, para usar las mismas unidades en ambos lados de la inecuación tenemos P(0.08xXx10000 > 900 ) = P(X > 9/8) = P(X > 1.125) = 0.375
Ejemplo 126
El tiempo medio en minutos que cierta persona invierte en ir de su casa a la estación de trenes es un fenómeno aleatorio que obedece una ley de distribución uniforme, en el intervalo de 20 a 25 minutos. ¿Cuál es la probabilidad de que alcance el tren que sale de la estación a las 7:28 a.m. en punto, si sale de su casa exactamente a las 7:05 a.m.?
Solución
Sea X la variable aleatoria definida como “El tiempo que la persona tarda en de su casa a la estación”. Como X se distribuye uniformemente en el intervalo (20, 25), entonces su función de densidad de probabilidad es f(x) = 1/5, 20 ≤ x ≤ 25.
Si sale de su casa a las 7:05 y el tren sale de su estación a las 7:28 entonces el tiempo que se tarde en llegar a la estación debe ser menor que 23 minutos; es decir, X < 23. La probabilidad de que esto ocurra es
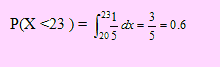
Ejemplo 127
Los trenes que se dirigen hacia el destino A llegan a una estación cada 15 minutos, comenzando a las 7:00 a.m., mientras que los trenes que se dirigen hacia el destino B llegan a la misma estación cada 15 minutos, comenzando a las 7:05 a.m.
Si cierto pasajero llega a la estación en un tiempo uniformemente distribuido entre las 7 y 8 a.m. y aborda el primer tren que llega, qué proporción de veces él va hacia el destino A?
Solución
El siguiente esquema pretende explicar la situación

Sea X la variable definida como “El tiempo que la persona tarda en ir de su casa a la estación”. X → U(7:00, 8:00). Esto implica que f(x) = 1/60, 0 ≤ x ≤ 60.
Puesto que la persona puede llegar entre las 7:0 y 8:0 a.m., para tomar el tren que va con destino a la ciudad A, debe llegar en los siguientes intervalos :
Entre las 7:05 a 7:15, entre las 7:20 y las 7:30; entre las 7:35 y las 7:45 y entre las 7:45 y las 8:0.
Esto significa que el tiempo que debe tardarse debe ser a lo más, de 10 minutos. Luego, si A representa el evento “La persona llega a tiempo a la estación”, P(A) = P(0 < X ≤ 10).
P(0 < X ≤ 10) es la integral de 0 a 10 de la funció de densidad f(x) = 1/60: el cual es 1/6.
Por otro lado, como dicha persona puede llegar antes de los 10 minutos, pero en cualquiera de los 4 intervalos mencionados, entonces, por el principio de la aditividad, P(A) = 4(1/6) = 2/3.
Distribución Exponencial
Sea X una variable aleatoria continua. Diremos que X tiene una distribución exponencial de parámetro α, si su función de densidad de probabilidad viene dada por
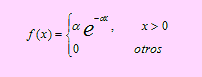
La gráfica de la función de densidad es aquella que se muestra en la siguiente figura

Si x = 0 entonces f(0) = ∞
Si x → ∞ entonces f(x) → 0
Si X se distribuye exponencialmente con parámetro α, entonces su función de distribución acumulada viene dada por

Nota:
Tenga presente a esta función ya que para calcular cualquier forma de probabilidad le será útil ya que no tendrá que estar integrando a f para la probabilidad pedida. Veamos algunos casos:
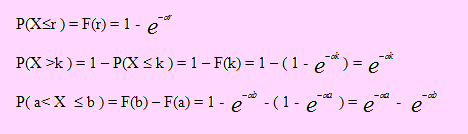
Teorema
Si X es una variable aleatoria con distribución exponencial, de parámetro α, entonces
μ = 1/α
σ2 = 1/α2
Usando MS Excel:
La función que permite resolver preguntas referidas a la distribución exponencial es:
P(X ≤ x) = Distr.Exp(x,α,opción)
Donde opción puede ser Verdadero ( 1) si se desea usar la distribución acumulada.
Ejemplo 128
La vida útil (en cientos de días) de ciertos repuestos para vehículos es una variable aleatoria que se distribuye exponencialmente con parámetro 2/3.
a) ¿Cuál es la probabilidad de que un repuesto de este tipo dure entre 110 y 130 horas?
b) Cuántos días durará un repuesto en el 90% de las veces?
c) ¿Cuántos días se espera que dure este tipo de repuesto?
d) Un perito inspecciona 5 repuestos de este tipo, ¿cuál es la probabilidad de que dos de ellos dure menos de 150 días?
Solución
Sea X la variable aleatoria que representa “La vida útil de dicho repuesto”. Como X tiene distribución exponencial de parámetro 2/3, entonces α = 2/3, con lo cual la función de densidad de probabilidad será

Según esto debemos hallar
a) P(110 ≤ x ≤ 130 ) = F(130) – F(110) = 1 - e-2/3(130) - ( 1 - e-2/3(110) ) = 0.244= 0.05995
Usando Excel: =Distr.Exp(1.3,2/3,1)-Distr.Exp(1.1,2/3,1)
b) De acuerdo a los datos tenemos P(X > c) = 0.90
Debemos encontrar c tal que se cumpla la igualdad. Usando la distribución acumulada, tenemos
P(X > c) = 1 – P(X ≤ c) = 1 – F(c) = 1 - (1 - e-2/3c)= e-2/3c.
Igualando a 0.90 y tomando logaritmo neperiano a ambos miembros tenemos: c = -(3/2)Ln(0.90) de donde c = 0.158 ; por lo que el repuesto puede durar hasta 6 días aproximadamente.
c) Puesto que X representa la vida útil del repuesto en cientos de días, E[X] representa el tiempo esperado de vida útil. Y como E[X] = 1/α, entonces E[X] = 3/2 = 1.5 cientos de días; es decir el número de días que se espera que dure este repuesto es de 150 días.
d) Por la naturaleza de la pregunta podemos definir a la variable Y como el “Número de repuestos cuyo tiempo de vida es inferior a 150 días”. Y puesto que se selecciona 5 repuestos, n = 5 y la probabilidad de éxito es p = P(X < 150 ).
Lo que tenemos es que Y es una variable cuya distribución de probabilidad es Binomial con parámetros n = 5 y p = P(X < 150).
Hallemos primero p:
p = P(X < 150) = F(150) = 1 - e-2/3(150) = 0.6321 Luego P(Y = 2 ) = C(5, 2)0.632120.36793 = 0.1990
Ejemplo 129
El tiempo de vida de una batería tiene distribución exponencial, con una desviación estándar de 6 horas. La utilidad por batería es el 20% de su costo C de fabricación cuando el tiempo es mayor que 6 horas; mientras que si dura menos de 6 horas, se pierde el 10% de su costo C. Para qué valor de C se tiene una utilidad esperada mayor que 0.1 por batería?
Solución
Sea Y la variable aleatoria definida como la utilidad por batería.
Según el problema, Y se define como

Decir que la utilidad esperada deba ser mayor que 0.1 por batería significa que E[Y] > 0.1. Será suficiente encontrar un valor de C tal que E[Y] = 0.1. De acuerdo a la definición de Y, tomando valor esperado a Y, tenemos
E[Y] = 0.20CP(X 6) + (-0.10C P(X < 6) = 0.20C(1-P(X<6)) – 0.10CP(X < 6)
=0.20C–0.30CP(X<6)=C(0.20 – 0.30x(1 - )= C(0.20 – 0.3x0.6321)=0.1036C
Haciendo 0.1036C = 0.1, de acuerdo al problema, obtenemos C = 9.65.
Para todo C / C > 9.65 se tendrá una utilidad esperada mayor que 0.1 por batería.
Ejemplo 130
Supongamos que el intervalo de tiempo entre la llegada de clientes a la ventanilla de un banco sigue una distribución exponencial con una media de 0.20 minutos. ¿Cuál es la probabilidad de que los clientes lleguen en un intervalo menor a los 10 segundos?
Solución
Sea X la variable aleatoria definida como “El intervalo de tiempo transcurrido entre la llegada de un cliente y el siguiente, medido en minutos”.
Como X tiene distribución exponencial con media μ = 0.20, entonces α = 1/0.20 = 5.
Luego la función de densidad de probabilidad de X viene dada por
f(x) = 5e-5x, x > 0.
Se pide encontrar la probabilidad de que los clientes lleguen a un intervalo menor a 10 segundos. Diez segundos es equivalente a 1/6 minutos. Pasamos a minutos por cuanto la variable X está definida en minutos.
Luego P(X < 1/6 ) = F(1/6) = 1 - e-5(1/6) = 0.5654
Ejemplo 131
Hallar, si existe, la función de densidad de probabilidad exponencial que cumple la siguiente condición:
P(X ≤ 3) = 2/3 P(X ≤ 3)
Solución
Si X tiene distribución exponencial con α su parámetro entonces, usando la condición propuesta tenemos

Si hacemos u = e-α entonces en (a), tenemos 2μu3 – 3μ2 + 1 = 0.
Resolviendo esta cúbica mediante el método de Ruffini, encontramos (u – 1)²(2u + 1) = 0 al reemplazar a μ por su valor y pretender resolver las ecuaciones con α, encontramos que no existe un α<>0 que satisfaga la condición planteada.
Ejemplo 132
La longitud de vida de una especie de planta en cierto medio ambiente es una variable aleatoria continua X, que tiene una distribución exponencial con una longitud media de vida de 1000 días.
a) ¿Qué proporción de plantas de esta especie mueren antes de los 1000 días?
b) Si una planta individual vive durante 800 días, ¿cuál es la probabilidad de que viva otros 400 días?
Solución
Sea X la variable aleatoria definida con la longitud de vida de esa especie de plantas
Como X tiene distribución exponencial con μX = 1000, entonces α f(x) = 1/1000 e-1/1000x x > 0, con lo cual
a) La proporción de plantas que mueren antes de los 1000 días es
P(X <1000 ) = F(1000) = 1 - e-1/1000(1000) = 0.6321.
Nota:
Este tipo de pregunta nos da oportunidad de comentar, mediante un ejemplo, la afirmación de que la distribución exponencial es una función como “ falta de memoria”.
Veamos por qué:
De acuerdo a lo dicho en la propiedad en cuestión, P(X>s + t /X> s ) = P(X > t ). En este caso, según el problema s = 800 , t = 400, por lo que, aplicando la propiedad tendremos
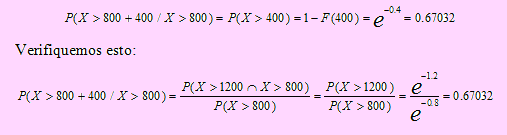
Ejemplo 133
Considere unos focos producidos por una máquina, de los que sabemos que su duración X, en horas, es una variable aleatoria con distribución exponencial y una media de 1000 horas.
a) ¿Cuál es la probabilidad de que una muestra aleatoria de 5 focos no contenga focos con duración menor que 1020 horas?
b) Supongamos ahora que la muestra de 5 focos se coloca en una caja. Si se selecciona aleatoriamente un foco de la caja, ¿cuál es la probabilidad de que el foco seleccionado tenga una duración mayor a 1020 horas?
Solución
Sea X la variable aleatoria definida como “El tiempo de vida un foco producido por esa máquina”.
Como X se distribuye exponencialmente con X = 1000, entonces = 1/1000 con lo cual
f(x) = 1/1000 e-1/1000x, x > 0.
a) Como se tiene una muestra de 5 focos, n = 5. Según la pregunta debemos hallar la probabilidad de que ninguno de estos focos tenga una duración menor a 1020 horas. Esto nos obliga a definir otra variable, digamos Y como “El número de focos cuya duración sea menor a 1020 horas”.
La probabilidad de éxito para una ocurrencia particular de Y es

b) Ahora se trata de seleccionar un foco de la caja que contiene 5 focos. La probabilidad de que este foco dure más de 1020 horas es
P(X > 1020) = 1 – P(X ≤ 1020) = 0.3606
Relación entre la distribución Exponencial y Poisson
Sea X la variable aleatoria definida como “El número de éxitos obtenido en un período de tiempo t”
Sea λ el parámetro que representa “El número de esperado de éxitos obtenidos por unidad de tiempo”. Esto significa que, en t unidades de tiempo, el número esperado de ocurrencias será λt , por ello, la distribución de probabilidad de X, así definida será

Ejemplo 134
En un conmutador telefónico se reciben llamadas de acuerdo a un proceso de Poisson con parámetro 5 por hora.
Si hay una persona en el conmutador,
¿cuál es la probabilidad de que transcurran al menos 15 minutos antes de la siguiente llamada?
¿De que no pasan más de 10 minutos?
Si ya han transcurrido 10 minutos desde la última llamada, ¿cuál es la probabilidad de que transcurran a lo más 5 minutos más para la siguiente llamada?
Solución
Sea X la variable aleatoria definida como “El número de llamadas telefónicas llegadas a dicho conmutador por hora”.
Por la forma de la definición de la variable, podemos decir que X tiene distribución de Poisson con parámetro λ = 5.
Sea Y la variable aleatoria definida como “El tiempo transcurrido antes que llegue la segunda llamada”, entonces Y tendrá distribución exponencial con parámetro α = λy.
Es decir f(y) = α e-λy, y ≤ 0.
A la pregunta: ¿Cuál es la probabilidad de que transcurran 15 minutos (0.25 horas), antes de la siguiente llamada?, respondemos encontrando la probabilidad de { Y / Y > 0.25 }; es decir,
P(Y > 0.25 ) = 1 – F(0.25) = 1 – (1 - e-5(0.25)) = 0.2865 La probabilidad de que no pasen más de 10 minutos( 1/6 horas) es
P(Y ≤ 1/6 ) = F(1/6) = 1 - e-5(1/6) = 0.5654
La última pregunta hace referencia a una probabilidad condicional. Para ello las conversiones de minutos a horas son: 15 minutos = 1/4 horas; 10 minutos = 1/6 horas.
Por ello debemos encontrar P(Y ≤ 5/12 / Y > 1/6 )
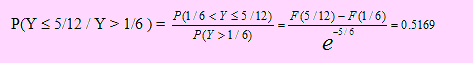
Ejemplo 135
El tiempo (en años) que un satélite permanece en el espacio es una variable aleatoria exponencial T, cuya función de distribución acumulada está dada por
F(t) = 1 - e-0.5t, t ≥ 0
Hallar la probabilidad de que un satélite permanezca en el espacio entre uno y tres años
¿Cuál es la probabilidad de que un satélite permanezca en el espacio más de cuatro años?
Si se lanzan tres satélites simultáneamente, ¿cuál es la probabilidad de que por lo menos uno permanezca en el espacio más de cuatro años?
Solución
Sea T la variable aleatoria que representa el “Tiempo que un satélite permanece en el espacio”. T tiene distribución exponencial con parámetro α = 0.5, según los datos.
Puesto que tenemos la función de distribución acumulada de T, usaremos a esta para responder a las preguntas
P( 1 ≤ T ≤ 3 ) = F(3) – F(1) = 1 - e-0.5(3) - (1 - e-0.5(1)) = 0.3834
Permanezca más de 4 años significa encontrar. P( T > 4 ) = e-0.5(4) = 0.1353
En este inciso observamos las siguientes características:
Número de veces que se realiza el experimento (nro. de satélites) n = 3
Probabilidad de éxito p = P(el satélite permanezca más de 4 años) = 0.1353
La permanencia de los satélites más de 4 años o no son eventos independientes.
Con estas característica, si definimos a X como el “Número de satélites que permanecen más de 4 años”, diremos que X tiene distribución Binomial con parámetros n = 3 y p = 0.1353 ( B(3, 0.1353) ). Si definimos ahora el evento A: Por lo menos uno permanezca más de 4 años, entonces debemos hallar
P(A) = P( X ≥ 1 ) = 1 – P( X < 1 ) = 1 – P(X = 0) = 1 – 0.13530(0.8647)3 = 0.35345
Ejemplo 136
Suponga que el tubo de imagen plana de un determinado tipo de televisor tiene una longitud de vida X (en años), la cual es una variable aleatoria exponencial con una vida media de 5 años.
Si el costo de fabricación de un tubo para estos televisores es de $ 40.0 y el fabricante vende a estos tubos a $ 75.0, garantizando un reintegro total si el tiempo de vida del tubo es menor a 4 años, cuál es el beneficio esperado por tubo del fabricante?
Solución
X es una variable exponencial definida como el tiempo de vida del tubo. Como en el caso de una distribución exponencial μ = 5 = 1/α, entonces α = 0.2.
Por otro lado, sea Y el beneficio del fabricante. Según el problema
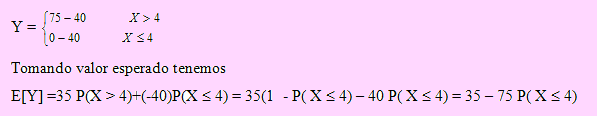
De donde
E[Y] = - 6.30. Esto significa que el fabricante espera tener una pérdida de $ 6.30 por tubo.
Ejemplo 137
Supongamos que X representa el tiempo de vida (en unidades de 1000 horas) de un determinado producto, el cual se considera como una variable aleatoria con función de densidad dada por
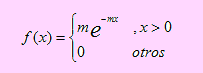
Donde m representa el factor de producción. El tiempo promedio de vida del producto es de 2000 horas.
a) Suponiendo que el costo de fabricación de tales productos es de $ 2.0, y el fabricante los vende por $ 5.0, pero garantiza un reembolso total si el tiempo de vida es, a lo más 900 horas. ¿Cuál es la utilidad esperada del fabricante?
b) Si ahora se selecciona cinco de estos productos aleatoriamente, ¿cuál es la probabilidad de que se obtenga por lo menos cuatro productos con tiempo de vida, a lo más, 900 horas?
Solución
Sea X la variable aleatoria definida como el “Tiempo de vida del producto”. Como X se distribuye exponencialmente, con una media de 2000 horas, entonces 1/α = 2000; de donde α = 1/2000.
Y puesto que m es el factor de producción y además coincide con α, entonces la función de densidad de X es f(x) = 1/2e-1/2x, x>0 (recuerde que X está en miles). La función de distribución acumulada de X es F(x) = 1 - e-1/2x.
a) Sea U la utilidad del fabricante.
De acuerdo a los datos, la utilidad es de (5-2) por producto siempre que el tiempo de vida, x es mayor que 900 (0.9 miles) será de (0-2) cuando x es menor a 0.9 puesto que el producto se devuelve, en cuyo caso sólo hay costo. La función que define a U es

Luego el valor esperado de U será
E[U] = 3P(X > 0.9) + (-2)P(X ≤ 0.9 ) = 3(1-P(X ≤ 0.9 ) –2P(X ≤ 0.9) = 3 – 5 F(0.9)
E[U] = 3 – 5(1 - e-1/2(0.9)) = 1.188.
Según esto, la utilidad que el fabricante espera obtener será de $1.188
b) En este caso se trata de obtener una muestra de 5 productos ( n = 5).
Definamos a la variable aleatoria Y como “El número de productos cuyo tiempo de vida no sobrepasan las 900 horas”.
De acuerdo al problema, Y se distribuye binomialmente con parámetros n = 5 y p; es decir Y → B(5, p), donde p = P(X 0.9 ) = 0.3624 Si A es el evento: “Obtener por lo menos 4 productos con tiempo de vida a lo más de 900 horas”, entonces
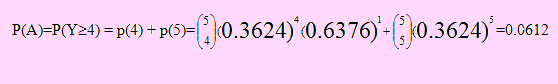
Distribución Normal
Sea X una variable aleatoria continua con -∞< X <+∞.
Diremos que X tiene distribución normal con parámetros μ y σ2 y si su función de densidad de probabilidad viene dada por

Del mismo modo
P(a ≤ X ≤ b) = F(b) – F(a)
Caso particular: Distribución NormalN(0, 1).
Sea X → N(μ, σ2). Si μ = 0 y σ2 = 1; es decir, si centramos la media de X en el origen de coordenadas y hacemos unitaria la varianza, entonces X → N(0,1) recibe el nombre de distribución normal 0,1 cuya función de densidad es f(x) = (1/√(2π)) e-x .
Analicemos esta función normal para obtener importantes conclusiones válidas para la solución de los problemas de aplicación.
En primer lugar, si hacemos a X = 0, entonces f(0) = 1/√(2π) = 0.39894228
La función f es una función simétrica respecto al origen de ordenadas Y. Esto implica que definimos un área bajo la curva para el intervalo (0, x0 ) con x0> 0, el área bajo la curva limitada por el intervalo (-x0 , 0), será la misma.

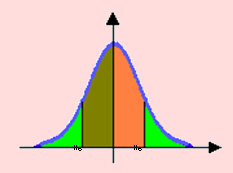
De acuerdo a lo expuesto en ii), P(X 0) = 0.5. Del mismo modo, también, P(X 0) = 0.5.
Dicho de otra manera F(0) = 0.5
Lo anterior significa que P[0 ≤ X ≤ x0 ] = P[x0 ≤ X ≤ 0 ].
Usando la acumulada F, tenemos F(x0 ) – F(0) = F(0) – F(-x0 ) de donde simplificando tenemos F(-x0 )= 2 F(0) - F(x0) . Luego F(-x0 ) = 1 – F(x0)
Adicionalmente, P(X ≥ x0 ) = P(X ≤ x0 ), como se puede ver en las áreas verdes. Afirmamos que P(X ≥ 4 ) = P(X ≤ -4 ) = 0, por aproximación, lo que se puede comprobar observando la siguiente gráfica
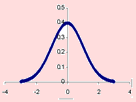
Por esta razón las tablas que usemos tendrán tabuladas a la función de distribución acumulada F desde X = -3 hasta X = 3, aunque cabe mencionar que también algunos libros muestran tablas desde X = -3.9 hasta X = 3.9, si bien sus últimos valores son iguales, a 5 decimales.
En la siguiente figura estamos mostrando el porcentaje de área cubierta por valores de μ y σ2 en los intervalos (μ-nσ, μ+nσ), tales como (μ-σ, μ+σ), (μ-2σ, μ+2σ) y (μ-3σ, μ+3σ).
En términos de probabilidades tenemos: P(-1 ≤ X ≤ 1) = 0.6826;
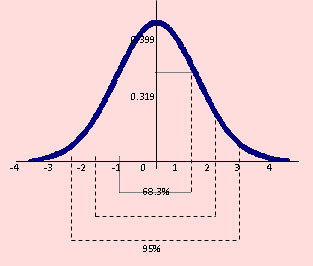
P(-1.645 ≤ X ≤ 1.645 ) = 0.9000;
P( -1.96 ≤ X ≤ 1.96 ) = 0.95;
P(-2.56 ≤ X ≤ 2.56 ) = 0.9896
Estandarizar una variable normal
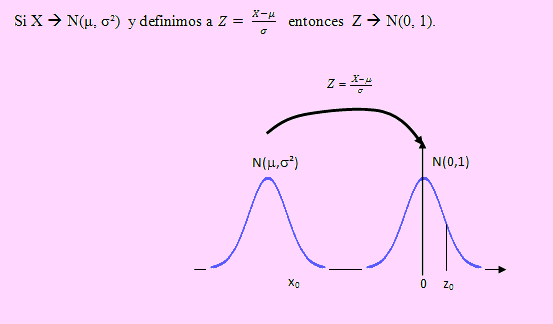
Ejemplo 138
Si X es una variable aleatoria distribuida normalmente con media = 6 y varianza ²=25, hallar
a) P(5 ≤ X ≤ 11 ) b) P( 0 ≤ X ≤ 8 )
c) P(-2 < X < 0) d) P(X > 21)
e) P(| X – 5 | < 5 ) f) P(|X - 5| < 10)
g) P(| X – 5 | > 14.8
El desarrollo de funciones para la distribución Normal es más completa que para otras. Posee funciones para el usao de la normal estándar N(0, 1) , para una normal cualquiera N(μ , σ ) y para obtener valores usando la función inversa.

Solución
Si X → N(5, 25), entonces μ = 5 y σ2 = 25 de donde σ = 5.
Resolvamos cada pregunta:

Ejemplo 139
Suponga que X tiene una distribución N(2, 0.16). Evalúe las siguientes probabilidades:
a) P(X ≥ 2.3)
b) P(1.8 ≤ X ≤ 2.1)
Solución
Si X → N(2, 0.16) entonces μ = 2 y σ2 = 0.16 de donde σ = 0.4.

Debemos hallar el z0 de la tabla para el cual Φ(z0 ) = 0.9772 Este valor es z0 = 2. Luego c/6 ) ( z0, de donde c = 12.
Ejemplo 141
Si X es una variable aleatoria que se distribuye normalmente con parámetros 3 y 4, hallara el valor de k si P(X ≥ k ) = 2 P(X < k).
Solución
Si X → N(3,4) entonces &my; = 3 y σ = 2.
Por ello
P(X ≥ k ) = 2 P(X < k) ⇒ 1 - P(X lt; k) = 2 P(X < k) ⇒ P(X lt; k) = 1/3.
Pasando a Z, tenemos que → N(0, 1), P/X < (k-3)/2) = 0.3333 de donde Φ((k-3)/2) = 0.3333. Como el área es menor que 0.5, el z que nos dé la tabla deberá ser negativo. Esto quiere decir que si se usa una tabla que muestra valores para z positivos, luego de encontrar el valor de z buscado, se debe cambiar de signo.
Por esta razón, si Φ((k-3)/2) = 0.3333 y el valor de z que da la tabla es –0.43, entonces (k-3)/2 = -0.43, de donde k = 2.14
Ejemplo 142
Los tubos fabricados por cierta máquina tienen un diámetro medio de μ 9.8 mm, con una desviación σ = 0.53 mm. ¿Qué porcentaje de tubos será rechazado, si no se aceptan diámetros inferiores a 9.0 mm? Asuma que los diámetros tienen una distribución normal.
Solución
Sea X la variable aleatoria definida como “La longitud del diámetro de un tubo”. Sea A el evento definido como “Longitud de diámetro inferior a 9.0 mm”; es decir A = {X/X<9 }. Como X → N(9.8, 0.53²) entonces P(A) = P(X < 9) = P(Z < (9-9.8)/0.53) = P(Z < -1.51) = &Phi:(-1.51) = 0.0655. Es decir, el 6.55% de los tubos fabricados por esa máquina serán rechazados.
Ejemplo 143
El diámetro de un cable eléctrico está distribuido normalmente con promedio 0.8 y varianza 0.0004. a) ¿Cuál es la probabilidad de que el diámetro sobrepase 0.81 pulgadas? b) Si el cable se considera defectuoso cuando el diámetro se diferencia en su promedio en más de 0.025, ¿cuál es la probabilidad de obtener un cable defectuoso?
Solución
Sea X la variable definida como la “Longitud del diámetro del cable eléctrico”.
a) Según el problema, X → N(0.8, 0.0004); esto es, μ = 0.8 y σ = 0.02.
P(Z > 0.81) = 1 - P(X ≤ 0.81) = 1 - P(Z < (0.81-0.8)/0.02) = 1-P(Z<0.5) = 1-Φ(0.5) = 1-0.6915 = 0.3085.
b) La frase “El diámetro se diferencia de su promedio en más de 0.025” se puede expresar matemáticamente como el evento A = {X/ |X - μ| > 0.025}. Y la probabilidad de que ocurra este evento es P(A) = 1- P(-0.025 /le; X - μ ≤ 0.025) de donde
P(A) = 1 - P(-0.025/0.02 ≤ Z ≤ 0.025 / 0.02) = 1 - P(-1.25 ≤ Z ≤ 1.25) = 1 - 2Φ(1.25) = 1-0.7888 = 0.2112
Ejemplo 144
Suponiendo que la duración de los instrumentos electrónicos D1 y D2 tienen distribuciones N(40,36) y N(45, 9), respectivamente. ¿Cuál debe preferirse para usarlo durante un período de 45 horas? ¿Cuál debe preferirse para usarlo durante un período de 48 horas?
Solución
Analicemos un poco los datos: La desviación en el primero es igual a 6 horas(supondremos horas ya que el problema no lo dice) mientras que en el segundo es de 3 horas.
Tanto el período de 45 horas como el de 48, presentan menor diferencia de medición, respecto a su promedio. Al dividir estas diferencias entre la desviación(para obtener Z) tendremos valores z0 de Z, para los cuales, P(Z < z0 ) será menor en el segundo tipo de instrumento, con lo cual preferiremos a éste. Bueno y qué tanto de razón tendremos en nuestra “sospecha lógica”? . Observe y analice la siguiente figura.
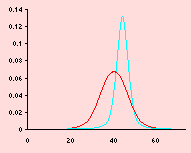
Analíticamente:
Si D1 → N(40,36) entonces μ1 = 40 y σ1 = 6.
Del mismo modo, si D2 → N(45, 9) entonces μ2 = 45 y σ2 = 3.
Se debe preferir aquel instrumento cuya probabilidad de duración en el período de 45 ó 48 horas sea mayor. Para averiguarlo, vamos a encontrar P(D1 < 45 ) y P(D2 < 45); y lo mismo haremos con el período de 48 horas. Veamos en el caso del período de 45 horas

Como en el primer caso, también aquí debemos preferir al segundo instrumento. Nuestra “sospecha lógica” estaba bien fundamentada.
Ejemplo 145
En un examen de suficiencia para ingresar al doctorado se tiene como calificación media la nota de 11 con una desviación igual a 2. Si se desea desaprobar al 40% de los examinados, ¿cuál debe ser la máxima calificación desaprobatoria?
Solución
Sea X la calificación obtenida por un postulante. Según el problema, X → N(11, 4). Por ello μ = 11 y σ = 2. Sea X0 la calificación máxima para desaprobar el examen. De manera que si X ≤ X0 el postulante desaprobará y P(X ≤ X0 ) es la probabilidad de que este evento ocurra.
Si queremos que el 40% desapruebe, entonces debemos hallar el valor de X0 tal que P(X ≤ X0 ) = 0.40.
Esto significa que P(X ≤ X0) = P(Z ≤ (X0-11)/2) = 0.40. El valor de Z0 para el cual se tiene un área igual a 0.40 es Z0 = -0.2575 (recuerde que siendo el área menor a 0.5 el Z que le corresponda será negativo y por otro lado, le rogamos que lea la nota para una adecuada aproximación de Z si la tabla no muestra el área que buscamos).
Continuemos: igualando el valor encontrado con Z0, tenemos (X0-11)/2) = -0.2575, de donde X0 = 10.485.
Luego la máxima calificación que debe considerarse para desaprobar el examen es 10.485
Ejemplo 146
Un ictiólogo esté interesado en estimar cuánto tiempo puede sobrevivir cierto tipo de pez de mar en aguas del río Amazonas. Luego de una serie de experimentos llega a estimar que la vida media de este tipo de peces alcanza los 210 días después de haber sido colocado en el agua del río, con una desviación estándar de 40 días.
El ictiólogo estima que la distribución de los días vividos es normal. Un pez particular ha sobrevivido 230 días, ¿cuál es la probabilidad de que sobreviva más de 240 días?
Solución
Supongamos que X representa “El número de días vida de cierto pez en las aguas del Amazonas”. Por los datos del problema X → N(210,1600), por lo que μ = 210 y σ = 40.
Sea A el evento “Un pez particular ha vivido 230 días” y B, el evento “Que dicho pez sobreviva 240 días”. Por la forma cómo se plantea la pregunta, debemos encontrar P(B/A), ya que es sabido de antemano que dicho pez ha sobrevivido los primeros 230 días.

Ejemplo 147
Un determinado programa del gobierno consiste en construir viviendas en los sectores de mayor densidad de Lima. Para la instalación de las redes de agua y desagüe se están utilizando tuberías en los que el 9.512% de ellos tienen una duración que exceden los 15 años y otra clase de tuberías en los que el 62.556% tienen períodos de duración que exceden los 9 años. Si se considera que la distribución de probabilidades del período de duración de estas tuberías es normal, determine los parámetros de esta distribución.
Solución
Sea X la variable aleatoria definida como “El período de duración de las tuberías”. De acuerdo a los datos P(X > 15 ) = 0.09512 y P(X > 9 ) = 0.62556. Usaremos estas dos igualdades para obtener dos ecuaciones con μ y σ, y luego proceder a resolverlas; naturalmente para ello, debemos pasar a Z y plantear cada ecuación por normal.

Ejemplo 148
El gerente de producción de una fábrica piensa que la vida útil de una máquina M está distribuida normalmente con una media de 3000 horas. Si el gerente piensa además que hay una probabilidad de 0.50 de que la máquina dure menos de 2632 horas ó más de 3368 horas, ¿cuál es la desviación estándar?
Solución

Ejemplo 149
Una empresa comercializadora, dedicado a la industria alimentaria distribuye harina en bolsas que llevan la etiqueta “Contenido neto: 500 Kg”.
La empresa consciente de la dificultad de los consumidores para adquirir bolsas de 500 gramos, está automatizando el llenado de las bolsas de forma que el peso medio de las mismas pueda ajustarse al nivel que se desee, a fin de bajar los precios(retirando previamente la etiqueta). Si la cantidad de harina por bolsa se considera una variable con distribución normal, con una desviación estándar de 0.2 onzas,
a) ¿A qué nivel debe ajustarse el llenado medio de modo que sólo el 0.1% de las bolsas tengan un peso neto inferior a 12 onzas?
b) ¿A qué nivel debe ajustarse el llenado medio de modo que sólo el 5% de las bolsas tengan un peso neto superior a 12.4 onzas?
c) El Gerente de comercialización decide cambiar los parámetros de ajuste si en una muestra de 10 bolsas encuentra más de 2 bolsas con peso inferior a 12 onzas, ¿cuál es la probabilidad de que el Gerente tenga que cambiar los parámetros?
Solución
Sea X la variable definida como “Cantidad de harina por bolsa”. Según el problema X tiene distribución normal N(μ, 0.2). Recuerde que 500 gramos de harina igual a 17.637 onzas.
a) Si se desea que sólo el 0.1% tengan peso inferior a 12 onzas, entonces P(X<12)=0.001. Esto permitirá encontrar el “llenado medio”, μ.
. P(X < 12) = P(Z < (12-μ)/0.2) = Φ(12-μ)/0.2).
Como esto es igual a 0.001, entonces (12-μ)/0.2 = Z0.001 = -3.01, de donde μ = 12.602. Luego el nivel medio debe ser de 12.6 onzas.
b) Como en el caso a), P(X > 12.4) = 1 - P(Z ≤ (12.4-μ)/0.2) ⇒ Φ( (12.4-μ)/0.2) = 0.95; de donde la media, μ =12.071 onzas. Esto es, el nivel medio por bolsa debe ser de 12.07 onzas.
c) En este caso se elige una muestra de tamaño n = 10. Sea Y la variable aleatoria definida como “Número de bolsas con peso inferiores a 12.4 onzas”. Esta variable tiene distribución Binomial B(n=10, p) donde p = P(X < 12.4) = 0.05. Debemos encontrar P( Y > 2) que será la probabilidad pedida.
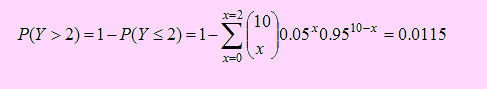
Ejemplo 150
En una distribución normal hay 40% de valores inferiores a 50 y 30% de valores superiores a 70. Determine el porcentaje de valores entre 55 y 70.
Solución
Sea X la variable definida en el problema con μ y σ2 sus parámetros.
Se sabe que P(X<50)=0.50 y P(X> 70 ) = 0.30.
Estas dos igualdades nos permitirán obtener los valores de μ y σ 2 para luego encontrar la probabilidad P( 55 ≤ X ≤ 70 ) que es el porcentaje pedido.
P(X < 50) = P(Z < (50-μ)/σ) = 0.40.
De donde obtenemos

Ejemplo 151
Una persona viaja diariamente de su casa a su centro de trabajo, y ha observado que el tiempo que tarda en llegar a su oficina tiene una media μ = 35.5 minutos, con una desviación estándar = 3.11 minutos.
Si sale de su casa todos los días a las 8:20 y debe estar en su oficina a las 9:0, ¿cuántos días al año espera llegar tarde? Suponer que el tiempo que tarda de su casa a su oficina sigue una distribución normal y que realiza 240 viajes anualmente.
Solución
Sea X la variable definida como “El tiempo que se tarda la persona en ir de su casa a su oficina”. X → N(35.5, 3.11). Si sale de su casa a las 8:20 y debe estar en su oficina a las 9:0 entonces el tiempo que se tarde en el viaje debe exceder los 40 minutos para llegar tarde. Esto significa que debemos encontrar P(X > 40).
Si ahora definimos a Y como “El número de veces que llega tarde a su oficina al año” , E[Y] será la cantidad de días que espera llegar después de las 9:0.
Como Y sigue una distribución binomial con n = 240 y p es la probabilidad de éxito, entonces E[Y] = np = 240p.
Por lo que será suficiente encontrar el valor de p = P(X < 40).
P(X > 40) = 1 - Φ(1-4471) = '-'75. Con lo cual E[Y] = 240(0.075) = 18
Luego la persona espera llegar tarde a su oficina 18 días durante el año.
Ejemplo 152
Un combustible para cohetes va a contener cierto porcentaje X, de un compuesto particular.
Las especificaciones exigen que X esté entre 30 y 35 por ciento. El fabricante tendrá una utilidad neta en el combustible(por galón) la que está definida según la siguiente función T
 ="">
="">Si X se distribuye normalmente como N(33,9), encuentre la utilidad neta esperada
Supóngase que el fabricante desea aumentar su utilidad neta esperada en 50% aumentando su utilidad por galón en aquellas partidas de combustible que satisfacen las especificaciones 30 < X < 35. ¿Cuál debe ser su utilidad neta?
Solución
Sea X la variable definida como “El porcentaje de cierto componente contenido en el combustible”.
Según a), X → N(33,9) implica que μ = 33 y σ = 3. Si E[T] es la utilidad neta esperada, entonces

que al resolver obtenemos para m = 0.1656, es decir el precio de la ganancia neta en las especificaciones 30 < X < 35 debe elevarse a $ 0.1656 para poder incrementar la utilidad neta esperada en 50%.
Ejemplo 153
Los gastos de publicidad que tienen el personal por la introducción en el mercado de un nuevo producto se distribuyen normalmente por semana con una media de $ 950.25 y una desviación de $ 30.35.
El gerente de ventas ha decidido premiar con una bolsa de viajes al personal de mercadeo si los gastos que realiza se encuentran en el 15% inferior. Si uno de los miembros del equipo en particular ha gastado $ 912, conseguirá la bolsa de viaje?
Solución
Definamos a X como “Los gastos semanales realizados en publicidad por un miembro del equipo de mercadeo”. Como X → N(950.25, 30.35²), entonces encontraremos la probabilidad P(X < 912), de manera que si esta probabilidad es menor que 0.15, entonces dicho empleado recibirá la bolsa de viaje.
P(X < 912) = P(Z < (912-950.25)/30.35) = Φ(-1.26) = 0.1038
Esto significa que el empleado recibirá la bolsa de viaje ya que 10.38% < 15%.
Ejemplo 154
El tiempo de vida de un determinado componente en ensamblaje de un carburador de automóvil tiene una distribución normal con media μ = 1170 días con una desviación estándar σ = 180 días. El costo de fabricación de cada uno de estos repuestos es de $ 8.0 y se vende en $ 11.0.
El fabricante garantiza la calidad de estos repuestos con la devolución del dinero si dicho repuesto deja de funcionar antes de los 36 meses de uso(un mes tiene 30 días).
Halle la utilidad esperada por cada repuesto
¿Qué cantidad de dinero se espera devolver en un lote de 100 repuestos vendidos?
¿Cuál es la probabilidad de que de un lote de 10 repuestos, a lo más tenga que devolverse el dinero en dos de ellos?
Solución
Sea X la variable definida como la vida útil del repuesto de carburador. Según los datos del problema, X → N(1170, 1802). Si U es la variable que representa la utilidad obtenida por repuesto, entonces
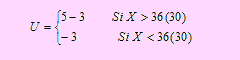
La utilidad esperada será E[U] = 2P(X>1080) – 3P(X<1080). Pasando a Z → N(0,1)
E(U) = 2P(Z > (1080-1170)/180) - 3P(Z > (1080-1170)/180)=2-5Φ(-0.5) = 2-5(0.3085) = 0.4575
Sea A el evento: “Devolver un repuesto que resulta defectuoso”
El evento A ocurre toda vez que el repuesto deja de funcionar antes de los 36 meses. La probabilidad de ocurrencia de A es P(A) = P(X < 1080) = P(Z<-0.5) = 0.3085.
La pregunta es: “¿Qué cantidad de dinero se espera devolver en un lote de 100 repuestos?”. La respuesta es: 5 x Nro. piezas que se espera devolver.
El Nro. de piezas que se espera devolver es 100 x P(A) = 30.85. Por ello, la cantidad de dinero que se espera devolver será 5(30.85) aproximadamente igual a $ 154.25
Para responder a esta pregunta debemos mirar al problema desde la perspectiva de otra variable: Tenemos un lote de 10 repuestos.
Si definimos a Y como el “Número de repuestos devueltos” entonces el evento definido en b) indica que P(A) = 0.3085 es la probabilidad de éxito para Y. Los valores que pueda tomar Y son 0, 1, 2, .., 10.
Como el hecho de que un repuesto sea devuelto o no, es independiente a lo que ocurra con otro, entonces podemos afirmar que Y tiene distribución binomial con B(n, p) en donde n = 10, p = P(A) = 0.3085).
Luego P(Y ≤ 2 ) = p(0) + p(1) + p(2) = 0.691510 + 10(0.3085)(0.6915)9 + 45(0.3085)2(0.6915)8 = 0.36043
Ejemplo 155
El gerente de Crédito de una determinada cadena de tiendas, estimó que los pagos mensuales, desde que asumió la dirección, siguen una distribución normal con un pago promedio de $10,000.0 y una desviación estándar de $ 1,500.0.
El gerente estudia la posibilidad de una tasa de descuento preferencial a sus clientes incentivándolos al pago de sus deudas que consiste en lo siguiente: Hasta el quinto inferior la tasa de descuento será del 3% mensual. Sobre la diferencia, y hasta antes del cuarto superior, la tasa de descuento será del 4% y para el cuarto superior será del 5% mensual.
a) ¿Cuáles son los límites de pago máximo y mínimo para acceder a una tasa de descuento preferencial mensual del 4%?
b) ¿Cuál es la probabilidad de que un cliente logre el máximo descuento para sus pagos?
Solución
a) Sea X la variable definida como “El pago realizado por los clientes de la cadena de tiendas”. El siguiente gráfico nos ayudará en expresar lo que queremos obtener.

Según esto, podemos afirmar que
P(X < L1 ) = 0.20
P(X > L2 ) = 0.25
P(L1< X < L2 ) = 0.55.
Resolviendo por normal la primera ecuación P(X < L1 ) = 0.20 encontramos L1 = 8737; del mismo modo, de P(X > L2 ) = 0.25 encontramos L2 = 11,012.50 b)
Puesto que el máximo descuento que se obtiene es $ 11,012.50, entonces el pago que el cliente haga debe estar en el cuarto superior, 0.25; que es justamente lo que se nos pide: P(X >11012.50) = 1 –P(Z < 1012.5/1500) = 1 – P(0.675) = 1-0.75 = 0.25