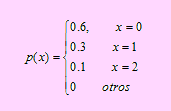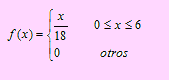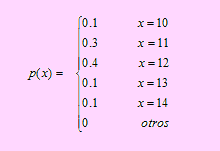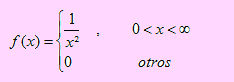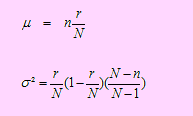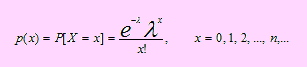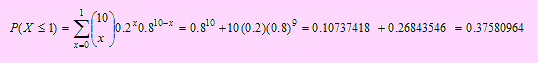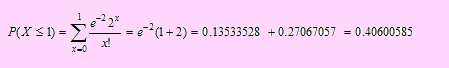4.8 PROBLEMAS PROPUESTOS

1. Una máquina posee 10 posiciones del torno diferentes que permite productos de diferente calibración. Si dicha máquina no tiene la unidad posicionada de manera apropiada, éste cae, y la posición del torno permanece abierta, resultando de ese modo un ciclo que produce menos de diez unidades. Un estudio del funcionamiento pasado de esta máquina indica que si X es una variable aleatoria que representa el número de posiciones abiertas, su función de probabilidad viene dada por


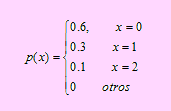
Si la pérdida debida a posiciones vacías viene dada por Y = 20x², encuentre
a) la función de probabilidad de Y
b) la media y varianza de Y (E(Y) y V(Y))

2. El contenido de cloro de un determinado compuesto es una variable aleatoria dada por la siguiente función de densidad de probabilidad:

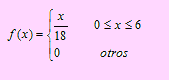
La utilidad que se obtiene de esta aleación es P = 10 + 2X
a) Encuentre la distribución de probabilidad de P
b) ¿Cuál es la utilidad esperada?

3. Un fabricante de aparatos de televisión a color ofrece un año de garantía de restitución gratuita si el tubo de imagen falla. El fabricante estima el tiempo de falla(en años), T, como una variable aleatoria con la siguiente distribución de probabilidad:


a) ¿Qué porcentaje de aparatos tendrá que reparar?
b) Si la utilidad por venta es de $200 y la sustitución del tubo de imagen cuesta $200, encuentre la utilidad esperada del negocio.
4. Un contratista ofrece realizar un proyecto. Los días requeridos, X, para la terminación sigue la siguiente distribución de probabilidad:

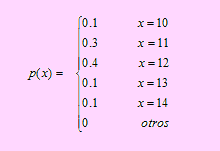
La utilidad del contratista es Y = 2000(12 – X)

a) Encuentre la distribución de probabilidad de Y
b) Determine E(X), V(X), E(Y) y V(Y).

5. El porcentaje de cierto aditivo en gasolina, determina el precio de venta. Si Z es la variable aleatoria que representa el porcentaje, entonces 0  Z  1. Si el porcentaje de Z es menor que 0.70, la gasolina es de 95 octanos y se vende a 9.92 soles por galón. Si el porcentaje de Z es mayor o igual a 0.70, la gasolina es de 97 octanos y se vende a 10.98 soles por galón.
Determine el ingreso esperado por galón en el caso en el que f(z) = 1, 0 ≤ z ≤ 1; y 0 en otros casos, f(z) = 0.

6. La estación terrena de Lurín tiene una antena rotatoria que recibe señales de dos formas. La posición rotacional(ángulo) se representa por X, y puede suponerse que esta posición en el tiempo en el que se recibe una señal es una variable aleatoria(por la variabilidad de la señal) con la densidad que se indica a continuación.
f(z) = 1/(2π)       0 ≤ x; ≤ 2π     y 0 en otros casos.
La señal puede recibirse si Y > y0, donde Y = tan(X). Por ejemplo, y0 = 1, corresponde a . Encuentre la función de densidad para Y.

7. La demanda de un anticongelante en una determinada temperatura se considera como una variable aleatoria X, con función de densidad definida por
f(x) = 10^-6, 10⁶ ≤ x ≤ 2x10⁶ donde X se mide en litros. Si el fabricante encuentra una utilidad de 50 centavos de dólar por cada litro que vende al final de año, y se debe conservar cualquier exceso durante el siguiente año a un costo de 25 centavos de dólar por litro, determine el nivel “óptimo” de existencias para un final de temporada particular.

4.9 DISTRIBUCIONES CONOCIDAS: CASO DE VARIABLE DISCRETA

Experimento de Bernoulli

Sea ζ un experimento y Ω el espacio muestral asociado a ζ. Supongamos que estamos interesados en la ocurrencia o no, de un determinado evento A ⊆ Ω. Diremos que este experimento constituye un Ensayo de Bernoulli si posee las siguientes características: La realización de este experimento genera dos únicos resultados posibles: ocurre el evento A o no ocurre; diremos que hay éxito si ocurre A, con p = P(A), probabilidad de éxito y diremos que hay fracaso si A no ocurre, en cuyo caso, si q representa la probabilidad de fracaso, entonces = 1 – p = 1 – P(A) = P(A’). Cada vez que se ejecuta el experimento p es siempre la misma; es decir, la probabilidad de éxito es constante.

La ocurrencia o no del evento A no influye en los resultados de la repetición del experimento; es decir, los resultados son independientes

Distribución de Bernoulli

Sea ζ un Experimento de Bernoulli y Ω, el espacio muestral asociado a . Supongamos que estamos interesados en la ocurrencia o no de un cierto evento tal como A. Sea p = P(A) la probabilidad de la ocurrencia de A. Si definimos a X como la variable aleatoria que representa “El número de veces que ocurre éxito cada vez que se realiza el ensayo de Bernoulli”, diremos que X es una variable aleatoria que tiene distribución de Bernoulli con parámetro “p”, entendida como la probabilidad de éxito. Usaremos como notación la siguiente expresión: X → Be(p) para indicar que la variable aleatoria X tiene distribución de Bernoulli con parámetro p.

Si X es una variable aleatoria que tiene distribución de Bernoulli, con parámetro p, entonces su función de distribución viene dada por
p(x) = P(X = x ) = p ( 1 – p ) ^{1 – x},     para X = 0, 1

Teorema

Si X es una variable aleatoria que tiene distribución de Bernoulli, entonces μ_X = E[X] = p     y σ²_X = V[X] = p (1-p) = pq

Distribución Binomial

Sea ζ un Ensayo de Bernoulli y Ω el espacio muestral asociado a ζ. Sea A el evento en el cual estamos interesados. Supongamos que dicho ensayo se repite n veces. Supongamos también que, cada vez que ocurre el evento A, diremos que se obtuvo éxito con probabilidad p y no hubo éxito con probabilidad q = 1 – p. Si X es una variable aleatoria definida como “El número de veces que ocurre éxito en las n repeticiones del experimento”, diremos que X es una variable aleatoria que tiene Distribución Binomial con parámetros n y p, lo cual denotaremos por X → B(n, p). Si X es una variable aleatoria que se distribuye binomialmente con parámetros n y p, entonces su distribución de probabilidad es

p(x) = P(X = x) = C(n, x) p^x(1-p)^n-x,       x = 0, 1, 2, ..., n.

Teorema

Si X es una variable aleatoria que se distribuye binomialmente con parámetros n y p, entonces

μ_X = E[X] = np
σ²_X = V[X] = n p (1-p) = npq

Problemas de Binomial usando Excel

Excel dispone de la siguiente función para resolver problemas de Binomial: = Distr.Binom(m,n,p,tipo)     = P(X ≤ k)
Donde
m: Representa el número de éxitos que se desea que ocurra
n : representa el número de veces que se realiza el experimento
p : representa la probabilidad de éxito
tipo : Es 1 o Verdadero si se desea P(X ≤ k). Es 0 o Falso si se desea P(X = k)

Ejemplo 85

Se lanzan dos dados cuatro veces. ¿Cuál es la probabilidad de que la suma 9 aparezca exactamente dos veces?

Solución

Si lanzamos una vez los dos dados, la probabilidad de que la suma sea 9 es 1/9. Llamemos a esta ocurrencia éxito, con lo cual p = 1/9.
Sea X la variable aleatoria que representa “El número de veces en que la suma es 9”. Según lo dicho, X tiene distribución binomial B(n = 4, p = 1/9).
Según la definición, su función de probabilidad será
p(x) = P(X = x) = C(4, x) p^x(1-p)^4-x     ,     x = 0, 1, 2, 3, 4.
De acuerdo a la pregunta, p(2) = P(X = 2) = C(4, 2)(1/9)²(8/9)² = 0.058527

Usando Excel:

P(X = 2) = Distr.Binom(2,4,1/9,0)

Ejemplo 86

Una máquina produce cierto tipo de piezas, de las cuales el 5% en promedio son defectuosos. En una muestra aleatoria de 5 piezas ¿cuál es la probabilidad de obtener a) exactamente dos piezas defectuosas? b) por lo menos una pieza defectuosa?

Solución

En este ejemplo la probabilidad de extraer una pieza defectuosa es 0.05. Esta probabilidad sigue siendo la misma cuando se extrae la segunda o las siguientes piezas, hasta completar los 5 de la muestra. No sabiendo cuántas defectuosas tiene el lote, supondremos que la probabilidad de éxito(la de extraer una pieza defectuosa) es constante. Por ello si X representa el número de piezas defectuosas en la muestra, entonces diremos que X tiene distribución Binomial y X → B(n=4, p=0.05).
Luego p(x) = P(X = x) = C(5, x)(0.05)^x(0.95)^5-x,     para x = 0, 1, 2, 3, 4, 5.

Respondamos ahora a las preguntas:

a) Exactamente dos piezas defectuosas significa encontrar
p(2) = P(X = 2) = C(5 , 2)(0.05)²(0.95)3 = 0.02143

Usando Excel:

P(X = 2) = Distr.Binom(2,5,0.05,0)

b) Por lo menos una pieza defectuosa significa es P(X ≥ 1)
P(X ≥ 1) = 1 – P(X < 1) = 1 – P(X = 0) = 1 – C(5, 0)(0.05)⁰(0.95)⁵ = 0.22622

Usando Excel:

P(X ≥ 1 ) = 1 – P(X < 1) = 1 – Distr.Binom(0,5,0.05,1)

Ejemplo 87

La probabilidad de hacer una venta en un intento, de cierto vendedor, es 1/2. ¿Cuál es la probabilidad de obtener
a) exactamente dos ventas en tres intentos de ventas consecutivas?
b) ¿por lo menos una venta en tres intentos de ventas consecutivas?
c) ¿Cuántos intentos de ventas consecutivas deben hacerse para obtener una seguridad de 0.9375 de obtener por lo menos una venta?

Solución

a) Si definimos a X como “El número de ventas en tres intentos de ventas consecutivas” y p = 0.5, con n = 3, diremos que X tiene distribución binomial con función de probabilidad definida por
p(x) = P(X = x) = C(3, x)(0.5)^x(0.5)^3-x = C(3, x)(0.5)³ , x = 0, 1, 2, 3
Según esto,
p(2) = P(X = 2) = C(3,2)(0.5)³ = 0.375
b) Por lo menos una venta significa que ocurre el evento X ≥ 1. Por lo que debemos encontrar P(X ≥ 1). Como P(X ≥ 1) = 1 – P(X = 0), entonces P(X ≥ 1) = 0.875
c) Por lo menos una venta significa X ≥ 1. De acuerdo a los datos, su probabilidad de ocurrencia es P(X ≥ 1) = 0.9375; es decir,
P(X ≥ 1) = 1 – P(X = 0) = 0.9375, de donde P(X = 0) = 0.0625
De acuerdo a la función de distribución,
P(X = 0) = C(n, 0)(0.5)ⁿ = 0.5ⁿ = 0.0625
Tomando logaritmo a ambos miembros tenemos n = Ln(0.0625)/Ln(0.5) = 4.25
Luego el número de intentos necesarios será 4, para tener la probabilidad de por lo menos una venta igual a 0.9375.

Ejemplo 88

Suponga que la máquina A produce el doble de artículos que la máquina B. Se sabe que el 6% de los artículos que produce la máquina A son defectuosos, mientras que solo el 3% de los artículos producidos por la máquina B son defectuosos. Si al final de un día de producción se juntan las dos producciones y de ella se toma una muestra aleatoria de 10 artículos, calcular la probabilidad de obtener tres artículos defectuosos.

Solución



El diagrama de árbol grafica claramente la característica del problema. Como lamáquina A produce el doble de artículos que la máquina B, entonces, al seleccionar un producto, la probabilidad de que este provenga de la máquina A es 2/3, y de que provenga de la máquina B es 1/3.

Por otro lado, un defectuoso puede provenir de la máquina A o de la máquina B; es decir la probabilidad de obtener un producto defectuoso del total de la producción de un día es p = (2/3)(0.06) + (1/3)(0.03) = 0.05. Esta es la probabilidad de éxito; la probabilidad de extraer un producto defectuoso.

Ahora volvamos al problema. Si X es el número de productos defectuosos en una muestra de n = 10 artículos, entonces X tiene distribución binomial con parámetros n = 10 y p = 0.05.
Luego su función de distribución es
p(x) = P(X = x) = C(10, x)(0.05)^x(0.95)^10-x     ;     x = 0, 1, 2, 3, …, 9, 10
Con lo cual
p(3) = P(X = 3) = C(10, 3)(0.05)³(0.95)⁷ = 0.01047

Ejemplo 89

El departamento de finanzas de una empresa capitalina contrata los servicios de dos empleados a tiempo parcial: Yaco y Báslavi. Yaco trabajará los Lunes, Miércoles y Viernes, mientras que Báslavi lo hará los Martes, Jueves y Sábado. Yaco archivó erróneamente uno de cada cinco documentos, mientras que Báslavi lo hace uno de cada seis. Con el propósito de evaluar los errores que ellos cometen, se elige un día de la semana y en ese día se toma una muestra de 6 documentos.
¿Cuál es la probabilidad de que la muestra contenga exactamente tres documentos mal archivados?
Suponiendo que la muestra contiene exactamente tres documentos mal archivados, ¿cuál es la probabilidad de que hayan sido archivados por Yaco?

Solución

Definamos la variable aleatoria X como el “Número de documentos mal archivados”. En primer lugar el número de documentos mal archivados por Yaco y por Báslavi es constante. Yaco archiva mal con probabilidad 1/5 y Báslavi, con probabilidad 1/6. Como la muestra de la que se extrae los documentos a ser examinados es n = 6, entonces X → B(n=6, p).
Encontremos el valor de p: la probabilidad de que el documento seleccionado de la muestra sea defectuoso.
Como Yaco y Báslavi trabajan el mismo número de días de la semana, la probabilidad de que se haya elegido uno de los días en los cuales trabaja Yaco, es 1/2. De suerte que la probabilidad de extraer un documento mal archivado por Yaco será p = (1/2)(1/5) + (1/2)(1/6) = 11/60, por cuanto Yaco archiva mal uno de cada 5, mientras que Báslavi lo hace uno de cada 6.

Ahora respondiendo a las preguntas, tenemos:
p(3) = P(X = 3) = C(6, 3)(11/60)³(49/60)³ = 0.0671

Sea X la variable aleatoria definida como el Número de documentos mal archivados.
Sea A el evento definido como “El documento fue archivado por Yaco”
Sea B el evento “Hay 3 documentos mal archivados”; es decir B = {x / x = 3 }
Según esto debemos buscar la probabilidad P(A/B).
Como P(A/B) = P(A ∩ B)/P(B). Debemos encontrar P(A ∩ B) ya que P(B) = 0.0671
P(A ∩ B) = P(A ∩ X = 3) = 0.5xC(6,3)(0.2)³x(0.8)³ = 0.04096
Luego
P(A/B) = P(A ∩ B) / P(B) = P(A ∩ X = 3) / P(X = 3) = 0.61019857

Ejemplo 90

Sea X una variable aleatoria con distribución binomial, cuya media es 12 y varianza 4.8.
Calcular P(X > 5)
P(5 < X < 10)
P( X < 10)

Solución

Si X → B(n,p) entonces μ _X = np = 12 y σ² X = np(1-p) = 4.8
Resolviendo el sistema de ecuaciones: 1 – p = 4.8/12 = 0.4 de donde p = 0.6.

Reemplazando p en la media obtenemos n = 12/0.6 = 20
Luego X → B(n=20, p = 0.4)



Usando Excel

P( X ≤ 10 ) = Distr.Binom(10,20,0.6,1)

Ejemplo 91

Un examen consta de 20 preguntas; cada una de ellas tiene 5 respuestas posibles de las cuales sólo una es la respuesta correcta.. Si un estudiante que desconoce el curso contesta la prueba aleatoriamente,
¿Cuál es la probabilidad de que acierte en más de 10 respuestas correctas?
¿Cuál es el número esperado de respuestas correctas?

Solución

De acuerdo a los datos, n = 20, p = 1/5 = 0.2 y si definimos a X como el “Número de respuestas correctas”, diremos que X tiene distribución binomial B(n=20, p = 0.2) y cuya función de probabilidad viene dada por


El número esperado de respuestas correctas será E[X] = np = 20(0.2) = 4

Ejemplo 92

El tiempo de arribo de clientes a la ventanilla de un banco, X, medido en minutos, es una variable aleatoria cuya función de densidad de probabilidad viene dada por


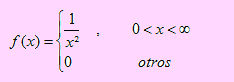
Si con el propósito de estudiar el comportamiento de los clientes se elige una muestra aleatoria de 8 personas, ¿cuál es la probabilidad de que al menos dos de las personas elegidas tengan un tiempo de llegada menor de 3 minutos?

Solución

Sea X la variable aleatoria definida como el tiempo de llegada a la ventanilla de un cliente. Esta es una variable continua. Puesto que se elige una muestra de 8 personas, y cada una de ellas tiene un tiempo de arribo determinado, estamos hablando entonces de otra variable: aquella que nos indica que pueden llegar 0, 1, 2,..., 7, 8 personas con un tiempo de arribo menor de tres minutos.
Por ello definiremos a Y como la variable que representa “Número de personas que llegan en menos de 3 minutos a la ventanilla”. Según esto, los valores de Y serán 0, 1,..., 7, 8. Esta variable Y tiene distribución binomial con parámetros n = 8 y p, la probabilidad de éxito que viene dada por la probabilidad de que el valor de X sea menor de 3 minutos; es decir,


Ejemplo 93

El 1% de habitantes de una cierta ciudad de Latinoamérica sufre de problemas de daltonismo. Si con propósitos de estudio se selecciona aleatoriamente, un conjunto de n habitantes de dicha ciudad, ¿cuál es la probabilidad de que ninguna de los n habitantes sean daltonianos? ¿Cuál debe ser el tamaño de la muestra elegida para que esta probabilidad sea menor al 10%?

Solución

Sea n el tamaño de la muestra y X la variable aleatoria definida como “El número de habitantes que tienen daltonismo”. Como la probabilidad de que un habitante cualquiera de dicha ciudad sea daltoniano es 0.01, entonces la probabilidad de éxito, p = 0.01; como el hecho de que uno de ellos sea daltoniano o no lo sea, no implica que algún otro lo sea, entonces X → B(n, p = 0.01).

Luego p(x) = P(X = x) = C(n, x) 0.01^x0.99^n-x,       x = 0, 1, 2, ..., n.

Si definimos el evento
A: “Ninguno de los habitantes es daltoniano”, entonces A = {X/ X = 0} P(A) = P(X = 0) = 0.99ⁿ

Ahora se trata de encontrar el valor de n, con la siguiente condición:
“La probabilidad de que ningún habitante sea daltoniano sea menor que 0.1”
Esta condición podemos expresarla simbólicamente como P(X = 0) < 0.1. Si resolvemos esta inecuación, hallaremos el valor para n, ya que P( X = 0 ) = 0.99ⁿ
Según a) tenemos P( X = 0) = 0.99ⁿ = 0.01 (Es suficiente encontrar una cota superior en la desigualdad, lo que nos permite resolver en términos de una ecuación).ⁿ 0.99ⁿ = 0.01 implica que ⁿ n Ln 0.99 = Ln 0.01, de donde n = 227, aproximadamente.

Ejemplo 94

En una feria, comprando un boleto de 10 pesos se puede participar en un juego que consiste en lanzar 6 argollas para insertarlo en una botella de madera. Los premios del juego son:
Una bolsa de caramelo(valor de un peso), al insertar de 1 a 3 argollas
Un tarro de duraznos(valor de 4 pesos), al insertar 4 argollas
Una botella de vino(valor de 17 pesos), al insertar 5 argollas
Una caja de cigarrillos(valor 31 pesos), al insertar las 6 argollas
Sabiendo que el jugador promedio tiene una probabilidad de 1/3 de insertar una argolla y que al día se vende en promedio 729 boletos; ¿cuáles son los ingresos netos diarios que el dueño del juego espera obtener.

Solución

Sea X la variable aleatoria que representa “El número de argollas insertadas al lanzar 6 de ellas”. Según esto, los valores de X son: 0, 1, 2, 3, 4, 5, 6.

Definimos a p = 1/3, la probabilidad de éxito de insertar una argolla. Como las 6 argollas representan la repetición de un ensayo de Bernoulli, entonces X tiene distribución Binomial B(n=6, p = 1/3), cuya función de densidad viene dada por


Si definimos a Y como la “Ganancia neta del dueño del juego”, entonces los valores que toma se muestran en el esquema anterior, con p(yi) = p(xi) , i = 1, 2, 3, 4, 5, 6
Debemos aclarar que ocurre Y = 9 cuando X = 1 ó X = 2 ó X = 3 con lo cual p(9) = 592/729

Encontremos ahora E[Y]:
E[Y] = (10)(64/729) + (9)(592/729) + (6)(60/729) + (-7)(12/729) + (-21)(1/729) = 6223
Es decir, la ganancia neta que el dueño espera recibir diariamente será de 6223 soles.

Distribución Hipergeométrica

Supongamos que se tiene una población finita de tamaño “N”. Supongamos que en esta población “r” elementos de ella poseen un determinado tipo de atributo. Supongamos también que en esta población se realiza el experimento de extraer una muestra de tamaño “n” sin reposición(sin reponer los elementos extraídos).

Si se define la variable aleatoria X como “El número de elementos en la muestra que poseen dicho atributo”, diremos que X tiene Distribución Hipergeométrica, de parámetros N, r y n lo cual denotaremos por X &rarr;  H(N, r, n). 

Si se define a X: “Número de éxitos obtenido en la muestra de tamañon” y definimos al evento A comoA = { x/ X = x }, entonces P(A) = p(x) = P(X = x) debemos calcularla usando el siguiente razonamiento;

P(A) = Número de casos favorables / Número de casos posibles

Si deseamos obtener x elementos de un total r elementos, el número de maneras de hacerlo es C(r, x) Del mismo modo, puesto que la muestra debe tener n elementos, los restantes n – x deben ser obtenidos de un total de N – r. El número de maneras de hacer esto es C(N - r, n - x).
Luego, el número de maneras de que x posean el atributo, y n – x, que no lo posean, es C(r, x) C(N - r, n - x), lo que constituye el “número de casos favorables”.
Por otro lado, si del total de N elementos se desea extraer muestras de tamaño n, el número de maneras de hacer esto es C(N, n).

Luego, la función de distribución de X será


Teorema

Si X es una variable aleatoria que tiene distribución Hipergeométrica, H(N, r, n), de parámetros N, r y n, entonces


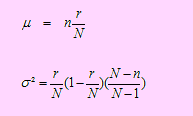
Ejemplo 95

De un lote que contiene 25 artículos, 5 de los cuales son defectuosos, se eligen 4 al azar. Sea X el número de artículos defectuosos encontrados. Obtener la distribución de probabilidad si los artículos se eligen sin sustitución.



Solución

Sea X la variable aleatoria definida como el número de artículos defectuosos elegidos en la muestra de tamaño 4.
Según la forma cómo se extraen los artículos, X tiene distribución Hipergeométrica con parámetros N = 25, r = 5 y n = 4; es decir X  H(25, 5, 4).

Si X = x es el evento “Elegir x artículos defectuosos”, entonces, x defectuosos se puede elegir de C(5, x) maneras mientras que 4-x no-defectuosos se pueden seleccionar de C(20, 4-x) maneras. Por ello, el número de maneras de elegir x defectuosos y 4 -x no defectuosos es, usando el principio de la multiplicación, C(5, x) C(20, 4 -x). Por otro lado, el número de maneras de extraer 4 artículos de un total de 25 es C(25, 4). Finalmente, si B = {X = x } entonces P(B) = C(5, x) C(20, 4-x) / C(25, 4), x = 0, 1, 2, 3, 4.

De manera que la función de probabilidad de X, viene dada por p(x) = P(X = x) = C(5, x) C(20, 4-x) / C(25, 4) , x = 0, 1, 2, 3, 4

Distribución Hipergeométrica en Excel:

En Excel para evaluar P(X ≤ k) se debe usar =Distr.Hipergeom(k,n,m,N)

donde k : Representa el número de éxitos deseado

n : Representa el número de experimentos o tamaño de la muestra

m : Representa el número de elementos que tiene el atributo deseado

N : Representa el tamaño de la población

Ejemplo 96

Sea X una variable aleatoria con distribución Hipergeométrica de parámetros N = 10, r = 6 y n = 5. Determine la verdad o falsedad de las siguientes proposiciones: El rango de X es R_X = {0, 1, 2, 3, 4, 5}
La distribución de probabilidad de X es p(x) = 1/252 C(6, x) C(4, 5-x), x = 0, 1, 2, 3, 4, 5.

El valor esperado de X es 3

La desviación estándar de X es 2

El valor esperado de X² es 2

El 100% de los valores de X son mayores que cero

Solución

Si X → H(N=10, r = 6, n = 5) entonces su función de distribución es p(x) = C(6, x) C(4, 5-x) / C(10, 5) , x = 0, 1, 2, 3, 4, 5       (1)

donde μ = n r/N y σ² = r/N (1 - r/N)((N-n) / (N - 1))     por lo que μ = 3 y σ² = 0.66667

Ahora veamos la verdad o falsedad de las proposiciones

Puesto que el tamaño de las muestra es n = 5 y r = 6, X toma valores 0, 1, 2, 3, 4 y 5. Por tanto R_X = {0, 1, 2, 3, 4, 5}. Luego es verdadera.

Dada la distribución en (1), resolviendo el denominador tenemos C(10,5) = 252. Luego la distribución de X puede ser expresada como se muestra. Verdadera.

El valor esperado de X, por lo que hemos visto, es  = 3 . Luego es verdadera.

Si σ² = 0.66667 entonces σ = 0.81649. La proposición es falsa.

Si V[X] = 0.66667 y V[X] = E[X²] – (μ²) entonces E[X²] = 9.66667. Falsa.

P(X > 0 ) = 1 – P(X = 0 ). El evento X = 0 significa extraer 0 de aquellos que cumplen cierta propiedad y por tanto, 5 de aquellos que no la cumplen. Puesto que éstos sólo son 4 y la muestra consta de 5, debemos extraer entonces, necesariamente un elemento de los que tienen la propiedad, es decir nunca ocurre el evento X = 0, por lo que P(X = 0) = 0. Luego P(X > 0 ) = 1. Por ello la proposición es verdadera.

Ejemplo 97

En una localidad muy alejada de la capital, se impugnaron los resultados de un proceso electoral. Por ello el Jurado Nacional de Elecciones procedió a examinar 10 mesas con un total de 1450 votos. De acuerdo a las actas del escrutinio, se tenía 48 votos impugnados. ¿Cuál es la probabilidad de que al elegir 5 votos del total de las 10 mesas, se encuentren por lo menos, 2 votos impugnados?

Solución

De acuerdo al esquema, X → H(1450,48,5)
Por ello p(x) = P(X = x) = C(48, x) C(1402, 5-x) / C(1450, 5)     x = 0, 1, 2, 3, 4, 5.
Sea A es el evento “Se encuentren por lo menos dos votos impugnados”.

P(A) = 1 – P(A’) = 1 – P(X < 2 ) = 1 – P(X = 0) – P(X = 1 ) = 1 - 0.84488 + 0.6057 = 0.145

En Excel

P(A) = P( X ≥ 2 ) = 1 – P(X < 2) = 1 – P(X ≤ 1 ) = 1 – Distr.Hipergeom(1,5,48,1450).

Ejemplo 98

María José, es la encargada de la elaboración de la planilla para los 11 trabajadores de su empresa. Debido a su estado emocional de ese día, confecciona 7 nóminas con errores. Puesto que esta no es la única vez que comete ese tipo de error, el Gerente de la empresa se encuentra descontento. Con la intención de tomar decisiones elige 5 nóminas aleatoriamente y encuentra errores en tres de ellas.
La Señorita María José se defiende argumentando que el porcentaje de error es muy bajo para ser tomado en cuenta. ¿Cree Ud. que este es un buen argumento?. ¿La teoría de probabilidades respalda este argumento?

Solución

De acuerdo a los datos, consideraremos como tamaño de la población, N = 11, con r = 7; tamaño de muestra, n = 5.
Sea X la variable aleatoria que representa el “Número de nóminas confeccionadas con error”. Según esto X  H(11, 7, 5).
Debemos hallar la probabilidad de que el número de errores en la muestra sea igual a 3. Si esta probabilidad es pequeña(digamos menor que 0.1), diremos que el argumento de la Señorita María José es válido y la teoría de probabilidades respalda su argumento, en caso contrario, estará equivocada y como tal, sus errores son probabilísticamente altas. Veamos
P(X = 3) = C(7, 3) C(4, 2) / C(11, 5) = 0.4545455

Luego el argumento de la Señorita María José no es válido

Distribución de Poisson

Sea X una variable aleatoria discreta que toma valores 0, 1, 2, ..., n-1, n, n+1, ...

Diremos que X tiene Distribución de Poisson cuyo parámetro es λ y su función de probabilidad es



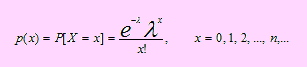
Notación

Usaremos la notación X → P(λ) para indicar que X tiene una distribución de Poisson.

Teorema

Si X una variable aleatoria con distribución de Poisson, entonces μ = λ y Σ² = λ.

Observación

El programa Excel no dispone de una función que permita evaluar probabilidades cuando se trata de variables con distribución de Poisson.

Ejemplo 99

Si X es una variable aleatoria con distribución de Poisson, con parámetro λ y si P(X = 0) = 0.2. Calcular P(X > 2).

Solución

Si X tiene distribución de Poisson con λ de parámetro, entonces p(x) = e^-λλ^x / x!.

Como P(X = 0) = e^-λλ⁰ / 0! = 0.2 entonces p(0) = = 0.2, de donde e^-λ = 0.2. Tomando logaritmo neperiano tenemos -λ = Ln(0.2), con lo cual λ = 1.6094.

Luego P(X > 2 ) = 1 – P(X ≤ 2) = 1 – [p(0) +p(1) + p(2) ] = 1 – 0.2(1 + 1.6094 + 1.6094²/2)
P(X > 2 ) = 0.21908

Ejemplo 100

Suponga que X es una variable aleatoria con distribución de Poisson.
Si P(X = 2) = 2/3 P(X = 1). Calcular P(X = 0) y P(X = 1)

Solución

Como P(X = 2) = 2/3 P(X = 1)   entonces e^-λλ² / 2!
.Al simplificar encontramos λ = 4/3.

Luego P(X = 0) = e^-4/3(4/3)⁰ / 0! = e^-4/3 ) = 0.26359

Del mismo modo, P(X = 1) = e^-4/3(4/3)¹ / 1! = 0.35146

Ejemplo 101

Si X es una variable aleatoria con distribución de Poisson tal que el 85% de sus valores son mayores o iguales que 1, ¿cuál es la probabilidad de que X tome como valor 2?

Solución

Si X → P(λ), entonces p(x) = P[X=x] = e^-λλ^x / x!.

Por ello, según los datos P(X ≥ 1) = 0.85.
Resolvamos esta ecuación para encontrar &lambda: y después encontrar P(X = 2).

P(X ≥ 1) = 0.85 implica que 0.85 = 1 – P(X < 1) = 1 – P(X = 0), de donde e^-&lamba;λ⁰ / 0! = 0.15.

Resolviendo para λ, tenemos λ = 1.8971

Por tanto P(X = 2) = (0.15)0.897119² / 2! = 0.26993

Ejemplo 102

El número de embarcaciones que llegan diariamente al muelle de Huacho tiene una distribución de Poisson con parámetro λ = 2. Las actuales instalaciones portuarias pueden atender un máximo tres embarcaciones por día. Si en un día determinado llegan más de 3 embarcaciones, todos los excedentes deben ser enviados al muelle de Huaura.
En un día determinado, ¿cuál es la probabilidad de enviar embarcaciones a Huaura?

¿En cuánto deben ampliarse las actuales instalaciones portuarias de Huacho para permitir la atención de aproximadamente el 90% de la demanda diaria?
¿Cuál es el número esperado de embarcaciones que llega diariamente?
¿Cuál es el número más probable de embarcaciones que llegan diariamente?
¿Cuál es el número esperado de embarcaciones atendidos diariamente?
¿Cuál es el número esperado de embarcaciones enviados a Huaura diariamente?

Solución

Si X → P(λ = 2) entonces p(x) = P[X=x] = e^-λλ^x / x!. , aquí X se define como “El número de embarcaciones que llegan al muelle de Huacho diariamente”. De acuerdo a esto
Si la capacidad de atención del muelle es hasta 3 embarcaciones, se debe enviar al muelle de Huaura siempre que X > 3. Esto se hace con probabilidad



Sea K la capacidad máxima de atención del muelle de Huacho después de ampliar hasta aproximadamente el 90% . La pregunta consiste en encontrar el valor de K.

Para ello tomemos en cuenta la suma de los valores dentro del paréntesis y que están indicados por las flechas. Dicha suma, como lo indica el lado derecho, es 0.85712. Si a ello le sumamos P(X = 4) = 0.09022, tendremos 0.94735. Esto quiere decir que si hacemos K = 4 entonces P(X ≤ 4 ) = 0.94735. Luego las instalaciones portuarias debieran ampliarse de tal forma que pueda atender hasta 4 embarcaciones, en aproximadamente el 90% del tiempo.

Por otro lado, puesto que E[X] = λ, siendo X la variable aleatoria que representa “El número de embarcaciones que llegan al muelle diariamente”, entonces  = E[X] representa el “Número esperado de embarcaciones que llegan diariamente”, esto es μ = λ = 2.

Ante todo diremos que “El número más probable” es el valor que toma una variable aleatoria para el cual se tiene el mayor valor de probabilidad que en todos los otros valores de la misma. Es decir, K será el valor más probable de X siempre que se cumpla que p(K) ≥ p(x), ∀x / x ε R_X . En el problema esto ocurre cuando X = 1 ó cuando X = 2. Luego es muy probable que lleguen al muelle de Huacho uno o dos embarcaciones diariamente.

Sea Y la variable aleatoria que representa “El número de embarcaciones atendidos diariamente”. Siempre que X  3 se atiende a la embarcación. Esto ocurre con P(X3)= 0.85712. Si por otro lado llegan en promedio dos embarcaciones, entonces El número esperado de embarcaciones atendidas será 2(0.85712) = 1.71424.

Igualmente, si cuando ocurre X > 3 se envía embarcaciones a otro muelle, y esto ocurre con P(X > 3 ) = 0.14288, el número esperado de embarcaciones enviadas a otro muelle será 2(0.14288) = 0.28576

Aproximación de Poisson a una binomial

Supongamos que se tiene la siguiente situación: El 6% de vehículos que transitan por las calles de Lima Metropolitana tienen tubos de escape defectuosos. Si un día determinado se seleccionan al azar a 100 automóviles y se les examina el tubo de escape, ¿Cuál será la probabilidad de que más de 20 de estos vehículos presenten un tubo de escape defectuoso?

Si definimos a X como “El número de automóviles cuyo tubo de escape es defectuoso”, con p = 0.06 y n = 100 entonces X B(n = 100, p = 0.06).



Esto ocurre cuando la probabilidad de éxito “p” es pequeño y n es lo suficientemente grande.
Una forma de obtener un resultado más aceptable es aproximar la solución mediante la distribución de Poisson.
Siendo X → B(n, p) con μ = np, y sabiendo que en el caso de una Poisson λ = μ, podemos utilizar la distribución de Poisson como una forma de aproximar problemas con distribución Binomial.

Teorema

Sea X una variable aleatoria distribuida binomialmente B(n, p) cuya función de distribución es


Ejemplo 103

Supóngase que la probabilidad de que un artículo producido por una máquina especial sea defectuoso es igual a 0.2. Si se seleccionan aleatoriamente 10 artículos producidos por esta máquina, ¿cuál es la probabilidad de que no se encuentre más de un artículo defectuoso? Use la distribución binomial y la de Poisson y luego compare los resultados.

Solución

Definamos a X como “El número de artículos defectuosos extraídos”. Según los datos del problema la probabilidad de éxito es p = 0.2 y el tamaño de muestra(número de repeticiones del experimento) es n = 10. Está demás decir que la variable tiene una distribución binomial con parámetros n y p. Por ello es natural responde a la pregunta resolviendo


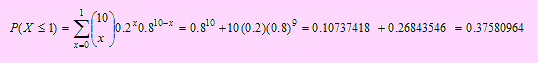
Si bien n = 10 no es suficientemente grande y p = 0.2 no es muy pequeño, de acuerdo a lo pedido en el problema, encontraremos una solución aproximada por la distribución de Poisson: En este caso μ = np = 10(0.2) = 2.
Por ello



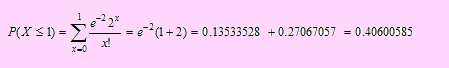
Puesto que n y p no satisfacen adecuadamente las condiciones para usar el teorema, es lógico que la aproximación no sea buena.

Veamos el siguiente ejemplo

Ejemplo 104

Una compañía de seguros ha descubierto que sólo alrededor del 0.1 por ciento de la población tiene cierto tipo de accidente cada año. Si 10,000 asegurados fueran seleccionados aleatoriamente de la población, ¿cuál será la probabilidad de que no más de 5 de estos clientes tengan un accidente de este tipo el próximo año?

Solución

Sea X la variable definida como “Número de clientes de dicha compañía de seguros que tiene ese tipo de accidentes al año”. X  B(n=10000, p=0.001). Si Ud. compara los datos de este problema con el anterior, verá claramente que debemos usar casi necesariamente el Terorema de la aproximación por Poisson. Por ello,  = np = 10000(0.001) = 10. Luego


Sugerimos a nuestro amable lector que encuentre la probabilidad pedida por Binomial. Creemos que en este caso el resultado debe ser 0.066991373, que ahora sí vale la pena aproximar por Poisson.

Ejemplo 105

En una planta ensambladora de equipos eléctricos han ocurrido cierto tipo de accidentes a razón de uno cada dos meses. Suponiendo que estos accidentes ocurren de forma independiente, ¿cuál es el número esperado de accidentes al año?. ¿Cuál es la desviación estándar del número de accidentes al año?. ¿Cuál es la probabilidad de que no haya accidentes de este tipo en un determinado año?

Solución

Si definimos a Y como el Número de accidentes cada mes, entonces Y es una variable aleatoria con distribución de Poisson en el cual la probabilidad de un accidente es p = 1/2
Puesto que los accidentes ocurren en un período de tiempo cuya longitud es de un año, definiremos a X como “El número de accidentes que se registra al año”. De acuerdo a esto, diremos que X sigue un proceso poissoniano por ello  =rp = 12(½) = 6.
El número esperado de accidentes al año es μ = λ = 6.
Como la varianza es la misma que la media, entonces %σ = √6 .
Finalmente P(X = 0 ) = e-6(6)0/0! = 0.60653

Ejemplo 106

Suponga que el número de reclamos que recibe cierta compañía telefónica, por semana, sigue una Ley de Poisson, de manera que la probabilidad de que ocurran dos reclamos es 2/3 de la probabilidad de que ocurra un reclamo. Calcular la probabilidad de que no ocurra ningún reclamo en tres semanas consecutivas.

Solución

Sea X la variable aleatoria definida como “El número de reclamos recibidos en una semana”. Como X tiene distribución de Poisson con parámetro λ, entonces p(x) = e^-λλ^x / x!. Por otro lado, puesto que P(X = 2 ) = P(X = 1) entonces de donde λ = 4/3.

Esto significa que el número de reclamos que la compañía telefónica reciba en un período de una semana es 4/3. Para responder a la pregunta definiremos otra variable Y que representa “El número de reclamos recibidos en tres semanas”. De acuerdo a lo dicho en el proceso poissoniano, Y tendrá también una distribución de Poisson con parámetro λ = rt = 3(4/3) = 4.

Por ello P(Y = 0 ) = e^-44^-0 / 0! = 0.018316

Ejemplo 107

Se estima que un libro de 400 páginas contiene 400 errores tipográficos repartidos aleatoriamente en todo el libro. Si se supone una distribución de Poisson, ¿cuál es el número de páginas que contienen
ningún error?
exactamente un error?
más de dos errores?
Si se seleccionan aleatoriamente 10 páginas de dicho libro, ¿cuál es la probabilidad de que ninguna de ellas tenga errores? Que 8 páginas no tengan errores?

Solución

Ante todo y de acuerdo a las primeras tres preguntas, definamos a X como “Número de errores por página”. Puesto que los errores se distribuyen por todo el libro, la probabilidad de que una página contenga un error de los 400 errores que hay, constituye la probabilidad de éxito p = 1/400, el cual guarda relación con la variable X. Por ello λ = np = 400(1/400) = 1 representa el número de errores por página del libro y es el parámetro de la distribución de X.

Luego, como X se define como número de errores por página.
P( X = 0 ) = e^-1 = 0.36789 con lo cual,
El número de páginas sin errores = 400(0.36789) = 147.152

Como P(X = 1) = 0.36789 entonces, el número de páginas con un error = 147.152

Si P(X > 2 ) = 1 – P(X ≤ 2) = 1- e^-1 (1 + 1 + 1/2) = 0.0803. Por tanto, el número de páginas con más de 2 errores será 400(0.0803) = 32.12

Definamos ahora a Y como el “Número de páginas sin error tipográfico”. Piense un poco en la forma cómo se define a X y para qué y también porqué debemos definir otra variable como Y, y por qué así.

En este caso, como se eligen 10 páginas, y Y es el número de páginas sin error, la probabilidad de éxito: que una página no tenga error es p = P(X = 0) = 0.36789.
Con este nuevo dato,
P(Y = 0) = C(10, 0)0.36789⁰(1-0.36789)¹⁰ = 0.010184
P(Y = 8) = C(10, 8)0.36789⁸(1-0.36789)² = 0.0060319

Ejemplo 108

Suponga que un libro de 585 páginas contiene 43 errores tipográficos. Si estos errores se distribuyen aleatoriamente a través del libro, ¿cuál es la probabilidad de que 10 páginas seleccionadas al azar, no contengan errores?

Solución

Sea X la variable aleatoria definida como “Numero de errores por página”. Según esto X puede tomar valores 0, 1, 2, ..., 43.
La probabilidad de que un error caiga en una página es p = 1/585. Usando el proceso poissoniano, X → P(λ) donde λ = np = 43(1/585) = 43/585.

Luego, la probabilidad de que una página tenga 0 errores es p(0) = P(X=0) = e^-43/585 =0.929

Por otro lado, para responder a la pregunta debemos definir otra variable tal como Y que represente: “Número de páginas sin errores”. Y de acuerdo a esta definición, la probabilidad de éxito será p = 0.929. Como por los datos Y → B(n=10, p = 0.929), entonces P(Y = 10) = C(10,10) 0.929¹⁰(1-0.929)⁰ = 0.4788

Ejemplo 109

Suponga que un libro de 1000 páginas contiene 500 errores tipográficos. Si estos errores se distribuyen aleatoriamente a través del libro,
¿Cuál es la probabilidad de que 2 páginas, de 10 seleccionadas al azar, no contengan errores.
¿Cuál es el número de páginas que no contienen errores?
¿Cuál es el número de páginas que contienen exactamente un error?

Solución

Como en los dos ejemplos anteriores, definamos a X como la variable que representa “El número de errores por página”. Por ello su probabilidad de éxito es p = 1/1000; es decir, la probabilidad de que un error caiga en una página. Como son 500 los errores, definimos a λ = 500(1/1000) = 0.5 como el parámetro de la distribución de X(Poisson). Por ello, la probabilidad de que una de las 1000 páginas no contengan error es P(X = 0 ) = e^-0.5 = 0.6065.

Sin embargo, para responder a la pregunta en a) debemos definir otra variable Y que represente “Número de páginas que no contienen errores”. En cuyo caso, su probabilidad de éxito es p = P(X = 0) = 0.6065 y Y → B(n = 10, p = 0.6065). Por tanto

P(Y = 2 ) = C(10, 2)0.6065²0.3935⁸ = 0.009515

El número de páginas que no contienen ningún error es 1000(0.6065) = 607

Volviendo a la distribución de probabilidad de X, debemos hallar P(X = 1), el cual es P(X = 1 ) = e^-0.5 (0.5) = 0.30325. Por lo que, el número de páginas que contengan exactamente un error será 1000(0.30325) = 303

Distribución geométrica

Sea ζ un experimento. Supongamos que estamos interesados en la ocurrencia o no de un evento, digamos A. Supongamos también que la probabilidad de que ocurra A es p, en cuyo caso diremos que ocurre éxito. Contrario a ello, q = 1 – p representa la probabilidad de la no ocurrencia de A, es decir, q es la probabilidad de fracaso.

Si este experimento se realiza indefinidamente “hasta que ocurra A, por primera vez” y definimos a X como el “Número de veces que se repite el ensayo hasta obtener éxito por primera vez”, diremos que X tiene distribución Geométrica con parámetro “p” cuya función de probabilidad viene dada por
p(x) = P(X = x) = p q^x-1,       x= 1, 2, 3, ....

Notación

X → G(p) significará que X es una variable aleatoria que tiene distribución geométrica con parámetro p.

Teorema

Si X es una variable que tiene distribución Geométrica entonces
μ = 1/p;       σ² = q/p²

Ejemplo 110

Sea X una variable aleatoria que tiene una distribución geométrica con parámetro p = 0.2. Determine la verdad o falsedad de las siguientes proposiciones:

El rango de X, es R_X = {0, 1, 2, 3, .....}
El valor esperado de X es 2
La varianza de X es 1/4
Como p = 0.2, el valor esperado de X² es 0.04
El 80% de los valores de X son mayores que 1

Solución

Puesto que X representa el número de veces que se realiza el experimento hasta que ocurra el primer éxito, X no puede tomar valor 0. Luego la proposición es falsa
De acuerdo al teorema, si E[X] = 1/p, y p = 0.2 entonces E[X] = 5. Es falsa la proposición
Como V[X] = q/p² = 0.8/0.04 = 20. La proposición es falsa.
Si V[X] = 20 y E[X] = 5 entonces E[X²] = V[X] + E[X]² = 25. Es falsa
P(X > 1) = 1 – P(X = 1 ) = 1 – pq0 = 0.8. La proposición es cierta

Ejemplo 111

Un juego de dados consiste en lanzar el dado hasta que salga un número múltiplo de 3. ¿Cuál es la probabilidad de ganar el juego en el quinto lanzamiento?

Solución

Puesto que el experimento consiste en lanzar una moneda hasta obtener un 3 o un 6, definamos a X como “El número de veces que debe lanzarse el dado hasta obtener por primera vez un número múltiplo de 3”.

Si definimos el evento A como “Se obtiene un número múltiplo de 3” entonces A = {3, 6} por lo que p = P(A) = 1/3 es la probabilidad de éxito, de obtener un número múltiplo de 3.
Luego por la definición de X diremos que tiene distribución geométrica X → G(p=1/3). Para que ocurra A en el quinto lanzamiento del dado, entonces debe ocurrir el evento X = 5. Por ello P(X = 5) = 1/3 (1-1/3)⁴ = 16/243 = 0.06584

Ejemplo 112

Se lanza el dado hasta que aparezca el 5. ¿Cuál es la probabilidad de que haya que lanzarlo más de 6 veces?

Solución

Como en el ejemplo anterior, sea X la variable aleatoria definida como el “Número de veces que se debe lanzar el dado hasta que aparezca el 5”. Aquí, X G(p = 1/6), por lo que debemos encontrar la ocurrencia del evento “X > 6”.


Ejemplo 113

En una población muy grande el 25% de las personas tienen ojos azules. Si se escogen aleatoriamente voluntarios de esta población, uno cada vez, hasta escoger a un voluntario de ojos azules, ¿cuál es la probabilidad de que la quinta persona sea la primera que tiene ojos azules? ¿Cuál es el número esperado de personas escogidas?

Solución

Sea A el evento “La persona escogida tiene ojos azules”, Si p es la probabilidad de éxito, entonces p = P(A) = 0.25. Si definimos a X como “El número de veces que debe repetirse el experimento hasta escoger a la primera persona de ojos azules”, entonces X G(p = 0.25).

Pedir que la quinta persona se la primera con ojos azules significa que el experimento se repite hasta que en el quinto se obtiene éxito.

Luego P(X = 5) = 0.25(0.75)⁴ = 0.0791
El número esperado de personas escogidas es E[X] = 1/p = 1/0.25 = 4.

Ejemplo 114

La máquina A produce el 5% de piezas defectuosas, mientras que la máquina B produce el 10%. Si se extraen piezas de la producción de cada una de ellas, alternativamente, hasta encontrar una pieza defectuosa, ¿cuál es la probabilidad de que de la producción A tenga que extraerse exactamente 4 piezas y de la producción B, exactamente 6 piezas?

Solución

Sea X la variable aleatoria definida como “El número de piezas extraídas de la producción A hasta obtener una defectuosa” y sea Y la variable aleatoria definida como “El número de piezas extraídas de la producción B hasta obtener una defectuosa”
Sea A el evento “Extraer una pieza defectuosa de A en la cuarta extracción” y
B el evento “Extraer una pieza defectuosa de B en la sexta extracción”

Según el problema, debemos encontrar P(A ∩ B).
X es una variable con distribución geométrica de parámetro p_A = 0.05 y Y tiene también una distribución geométrica con parámetro p_B = 0.10.
Luego P(A) = p(4) = P(X = 4) = 0.05(0.95)³ = 0.04286875 P(B) = p(6) = P(Y = 6) = 0.10(0.90)⁵ = 0.059049.
Con lo cual P(A ∩ B) = 0.002536.

Ejemplo 115

En una población estudiantil que se reúnen todas las mañanas en el patio, se encuentra que, en un día determinado, los 2/3 de los alumnos están ausentes debido a una epidemia en la zona. Si el Profesor Díaz Cubas pasa lista en su sección de 25 alumnos y definimos a X como el número de alumnos que deben ser llamados hasta encontrar a uno conteste presente,
¿Cuál es la probabilidad de que el décimo niño llamado sea el primero que responda presente?
Calcular P(X <3)
Encuentre el número esperado de alumnos ausentes y la desviación estándar.

Solución

Si X es la variable definida como “El número de alumnos que deben ser llamados hasta que uno responda presente”, entonces X tiene distribución Geométrica con parámetro p = 1/3. Esto es así por cuanto los 2/3 de los alumnos están ausentes. La función de distribución de X es p(x) = P(X = x) = (1/3)(2/3)^10-x    , x = 1, 2, ...
P(X = 10) = (1/3)(2/3)⁹ = 0.00867
P(X < 3 ) = P(X ≤ 2) = (1/3)(2/3)⁰ + (1/3)(2/3) = 5/9
El número esperado de alumnos ausentes es E[X] de manera que E[X] = 1/p = 3
Puesto que la desviación estándar es σ² = q/p², entonces σ = 2.4495

Distribución de Pascal

Supongamos que se realiza un experimento ζ de manera repetida observando sus resultados. Si definimos a X como el “Número de veces que debe repetirse el experimento hasta obtener r resultados exitosos” y definimos a p como la probabilidad de éxito cada vez que se realiza el experimento, diremos entonces, que X tiene Distribución de Pascal con parámetros r y p, cuya distribución de probabilidad viene dada por


Teorema

Si X es una variable que tiene distribución de Pascal, entonces μ = k(1/p) y σ² = k(q/p²)

Ejemplo 116

Si se lanza una moneda hasta que obtener 5 caras, encuentre la probabilidad de que tenga que lanzarse 12 veces. Encuentre también el número esperado de veces que debe lanzarse la moneda para obtener 5 caras, así como su desviación estándar.

Solución

Definamos a X como la variable aleatoria que representa “El número de lanzamientos realizados hasta obtener 5 caras”. X → Pk(r = 5, p = ½ ). El espacio rango de X es 5, 6, .. Como sólo se deben realizar 12 lanzamientos, la quinta cara debe obtenerse en el décimo lanzamiento. Las otras 4 caras deben caer en los 11 lanzamientos anteriores. Ahora bien, ¿de cuántas maneras podemos repartir 4 caras en 11 posiciones? Esto se hace en C(11,4) maneras. Como por otro lado deben obtenerse 5 caras y la probabilidad de obtener una cara es ½ , entonces ( ½ )⁵ es la probabilidad de obtener 5 caras. Además, Como en 12 lanzamientos deben ocurrir 7 sellos entonces ( 1/2 )⁷ es la probabilidad de obtener 7 sellos. Luego, la probabilidad de obtener 5 caras y 7 sellos es ( ½ ) 5 ( ½)7. Y esto puede ocurrir en C(11,4) maneras.
Luego
P(X = 12) = C(11, 4) (1/2)⁵(1/2)⁷ = 0.0856

El número esperado de veces que debe lanzarse la moneda hasta tener 5 caras es 5(1/(1/2)) = 10.
Del mismo modo, la desviación estándar, es 5(1/2 / ( 1/2 )²) = 10

Ejemplo 117

La probabilidad de un lanzamiento exitoso es igual a 0.8. Suponga que se hacen ensayos de lanzamiento hasta que 3 de ellos sean exitosos. ¿Cuál es la probabilidad de que sean necesarios 6 intentos?

Solución

Sea X la variable aleatoria definida como “El número de lanzamientos realizados hasta que tres de ellos sean exitosos”. Por la forma cómo se define a X, sin duda ella tiene distribución de Pascal con parámetros r = 3 y p = 0.8; es decir X → Pk(3, 0.8) y cuya distribución de probabilidades viene dada por
p(x) = P(X = x) = C(x-1, r-1)0.8^r0.2^x-r. Según esto,
p(6) = P(X = 6) = C(6-1, 2)0.8³0.2^6-3 = 0.04096

Ejemplo 118

Supongamos que un inexperto vendedor sale a las calles a ofrecer un determinado producto de playa. La probabilidad de que realice una venta efectiva es 0.05. Si un día domingo él decide ofrecer su producto hasta obtener 5 ventas efectivas, ¿cuál será la probabilidad de que tenga que ofrecer su producto a 20 clientes?

Solución<

Si X representa “El número de clientes a los que debe ofrecer su producto hasta lograr que 5 de ellos compren” entonces X tiene distribución de Pascal con parámetros r = 5 y p = 0.05. Luego p(5) = P(X = 5) = C(19, 4)0.05⁵0.95¹⁵ = 0.000561

Ejemplo 119

Las máquinas A y B producen, en promedio, 5% y 10% de piezas defectuosas, respectivamente. Suponga que se extraen piezas de la producción de cada una de ellas, hasta obtener 3 piezas defectuosas. ¿Cuál es la probabilidad de que tenga que extraerse 6 piezas de la producción de A y 4 de la producción de B?

Solución

Sea X la variable aleatoria definida como “El número de piezas extraídas de la producción de A hasta obtener 3 piezas defectuosas”.
Sea Y la variable aleatoria definida como “El número de piezas extraídas de la producción de A hasta obtener 3 piezas defectuosas”.
Según los datos: X → Pk(r = 3, p = 0.05) y Y → Pk( r = 3, p = 0.10).

En cuanto a la máquina A:
p(6) = P(X = 6) = C(5, 2) 0.05³0.95³ = 0.00107

En cuanto a la máquina B:
p(4) = P(X = 4) = C(3, 2) 0.05³0.95¹ = 0.000356

Distribución Multinomial

Sea X₁ , X₂ , X₃,... X_r , un conjunto de variables aleatorias definidas como el “Número de veces que se repite cada una de ellas” con n_i el número de veces que se repite X_i , diremos que X₁ , X₂ , X₃,... X_r tienen distribución multinomial si
P(X₁ = n₁ ,₂ = n₂ , ..., _r = n_r) = n! / (n₁!n₂!...n_r!)p₁^n₁p₂^n₂...p_r^n_r)
donde n = n₁ + n₂ + ... +n_r

Teorema

Si X₁ , X₂ , X₃,... X_r son variables aleatorias que tiene una distribución multinomial, entonces su esperanza es E[X] = np_i     y
Su varianza V[X] = np_i (1- p_i ) para i = 1, 2, ..., r

Ejemplo 120

Un mecánico mantiene un gran número de arandelas en un depósito. El 50% de estas arandelas son de ¼ de pulgadas de diámetro; el 30% de ellas son de 1/8 de pulgadas y el 20% son de 3/8 de pulgadas de diámetro. Supongamos que se elige 10 arandelas de este depósito.
¿Cuál es la probabilidad de que haya exactamente 5 arandelas de ¼ de pulgada, 4 de 1/8 de pulgada y uno de 3/8 de pulgada?
¿Cuál es la probabilidad de que hay sólo dos tipos de arandelas entre las elegidas?
¿Cuál es la probabilidad de que haya 3 de una clase, 3 de otra clase y 4 de otra clase?

Solución

Sea X₁ la variable aleatoria que representa el número de arandelas de ¼ de pulgada.
Sea X₂ la variable aleatoria que representa el número de arandelas de 3/4 de pulgada.
Sea X₃ la variable aleatoria que representa el número de arandelas de 3/8 de pulgada,
De acuerdo a esto, el conjunto de variable X1, X2 y X3 tienen una distribución multinomial con probabilidades de éxito 0.5, 0.3 y 0.2, respectivamente.
Por ello debemos encontrar

4.10 PROBLEMAS PROPUESTOS

Distribución binomial

1. Deduzca la distribución de probabilidad de una variable con Binomial y obtenga su media y varianza.

2. Sea X la variable aleatoria con distribución binomial de parámetros n = 4, p = 0.5. Si el espacio rango de X es { 0, 1, 2, 3, 4 }, encuentre la función de probabilidad de X y construya su gráfica.

3. En una universidad latina, el 70% de los estudiantes de postgrado que obtienen el grado de Doctor en biología en ese país, son ciudadanos de otros países. Considere el número de estudiantes extranjeros en una muestra de 25 estudiantes de ingeniería recientemente graduados y luego
a) Calcule P(X = 10)
b) Calcule P(X ≤ 15)
c) Calcule la media y la desviación estándar de X. Interprete estos resultados.

4. En un trabajo de investigación se reportó que el 1% de todos los trabajadores de la industria de la construcción son mujeres. En una muestra aleatoria de 10 trabajadores de esta industria, encuentre la probabilidad de que cuando más, uno de ellos sea mujer.

5. En un estudio reciente, Data Consult encontró un gran número de casos de contaminación y errores de etiquetación de conservas en los supermercados de Lima. El estudio reveló un resultado alarmante: el 40% de trozos de anchoveta, disponible para la venta, tenía un nivel de mercurio superior al límite inferior establecido. Para una muestra aleatoria de tres trozos anchoveta, calcule la probabilidad de que
a) Los tres trozos de anchoveta tengan niveles de mercurio por encima del límite permitido.
b) Exactamente uno de tales trozos esté por encima del límite permitido.
c) Cuando más, uno de tales trozos esté por encima del límite.

6. Un estudio de tendencias a lo largo de cinco años en los sistemas de información logística de la industria reveló que los mayores avances en la computación, tuvieron lugar en el transporte. Actualmente el 90% de todas las industrias contienen archivos de pedidos abiertos de embarque en su base de datos computarizada. En una muestra aleatoria de 10 industrias, sea X el número de ellas que incluyen archivos de pedidos abiertos de embarque en su base de datos computarizada.
a) Calcule la probabilidad de que haya más de 5 que incluyen archivos de pedidos.
b) Encuentre la media y varianza de la variable X

7. Los registros de una pequeña compañía de servicios indican que el 40% de las facturas que envían son pagadas después de la fecha de vencimiento. Si se envían 14 facturas, cuál es la probabilidad de que
a) ninguna se pague con retraso
b) cuando menos dos se paguen con retraso
c) cuando menos la mitad se pague con retraso

8. Una compañía de exploración petrolera observa que en casi el 5% de los pozos de prueba que perfora, encuentra un depósito de gas natural. Si se perfora 6 pozos, encuentre la probabilidad de que al menos en uno de ellos se encuentre gas.

9. Una prueba de opción múltiple presenta cuatro opciones por pregunta y consta de 14 preguntas. Si la calificación aprobatoria depende de obtener nueve o más respuestas correctas, cuál es la probabilidad de que un estudiante que adivina todas sus respuestas apruebe el examen?

10. Una compañía de bienes raíces observa que uno de cada diez compradores potenciales de casas prometen comprar una si vuelven a consultar por segunda vez. En 10 de estos casos, encuentre la probabilidad de que ninguno compre una casa.

11. En una encuesta reciente se concluyó que sólo el 15% de médicos de un área rural faltan a sus turnos. Se observó que dos de los ocho médicos seleccionados de una lista suministrada por el directorio médico local, también faltan a sus turnos. Suponiendo que la encuesta esté en lo correcto, ¿cuál es la probabilidad de obtener este resultado?

12. Las investigaciones médicas señalan que el 20% de la población general, sufre efectos negativos colaterales al ingerir un nuevo fármaco. Si un médico receta dicho fármaco a cuatro pacientes, ¿cuál es la probabilidad de que
a) ninguno sufra efectos colaterales
b) al menos uno presente efectos colaterales

13. En una reciente encuesta gubernamental se encontró que el 80% de las familias que viven en una comunidad suburbana, y cuyos ingresos brutos son superiores a $ 15,000 poseían dos autos. Suponiendo que el estudio esté en lo cierto y si selecciona una muestra de 10 familias de esta categoría, obtenga la probabilidad de que exactamente el 20% de los que integran dicha muestra tengan dos autos.

14. Un televisor que presenta 10 series de circuitos tiene uno defectuoso. Ocho de las series son difíciles de reemplazar. Encuentre la probabilidad de que la serie defectuosa no sea una de ellas.

15. Los informes de tránsito indican que el 25% de los vehículos que se detienen en una autopista interestatal no satsifacen las normas de seguridad. Si se detienen 16 vehículos y se les somete a revisión, encuentre la probabilidad de que
a) dos o más no satisfagan las normas de seguridad
b) cuatro o más no las satisfagan
c) nueve o más no las cumplan

16. Un comentarista deportivo acierta al señalar al ganador en 6 de 10 partidos de fútbol. Si una persona simplemente está adivinando, ¿cuál es la probabilidad de que pueda igualar o superar dicha marca?

17. Según los archivos universitarios, de los estudiantes de una escuela de enseñanza media superior, el 15% cambia de especialidad por lo menos una vez durante su primer año de estudios. Si se selecciona 10 estudiantes de los grupos del primer año, encuentre la probabilidad de que por lo menos nueve hayan cambiado.

18. Una gran urna contiene 10 mil canicas de colores, distribuidos según el siguiente cuadro:

 

Blancas	5000
Verdes	3000
Rojas	1500
Negras	500

Si se escogen 20 canicas, encuentre la probabilidad de que haya dos verdes.

19. Remesas de 500 productos cada una son aprobadas si en una muestra aleatoria de 10 se hallan menos de dos defectuosos. Si en realidad una remesa tiene el 5% de artículos defectuosos, ¿cuál es la probabilidad de que sea aprobada?

20. En el problema anterior, qué porcentaje de lotes con 10% de productos defectuosos producirán muestras de 10 artículos en las que ninguno estuviera defectuoso?

21. Un mecánico sabe, con base en su experiencia, que el 90% de los accesorios que desecha al ser reemplazados por otros nuevos, se pueden usar de nuevo. Si para un trabajo se requieren 5 piezas reutilizables, ¿cuál es el número mínimo de piezas desechadas que deberá obtener si desea que la probabilidad de devolver partes sobrantes sea menos de 0.12?

22. La mayor cantidad de quejas de propietarios de automóviles con dos años de uso se debe al funcionamiento eléctrico. Suponga que un cuestionario anual se manda a propietarios de más de 300 modelos y marcas de automóvil, y resulta que el 10% de propietarios de automóviles con dos años de antigüedad han tenido problemas con los componentes del sistema eléctrico, incluyendo el motor de arranque, el alternador, la batería, los interruptores, los instrumentos, el cableado, las luces y el radio.
a) ¿Cuál es la probabilidad de que en una muestra de 12 propietarios de automóviles con dos años de uso, haya exactamente dos con problemas en el sistema eléctrico?
b) ¿Cuál es la probabilidad de que en una muestra de 12 propietarios haya cuando menos dos con problemas en el sistema eléctrico?

23. Cuando una máquina nueva funciona bien, sólo el 3% de los artículos que produce tienen defectos. Suponga que se selecciona al azar dos partes producidas por la máquina y que interesa la cantidad de partes defectuosas encontradas.
a) Describa las condiciones bajo las cuales este caso sería un experimento binomial.
b) Trace un diagrama de árbol que muestre un experimento binomial.
c) Cuántos de los resultados experimentales consisten en encontrar exactamente un defecto?
d) Calcule la probabilidades asociadas con: no encontrar defectos, encontrar exactamente un defecto y dos defectos.

Distribución de poisson

24. Las llamadas de emergencia registradas en un conmutador de una estación policial son 4 por hora en un fin de semana cualquiera y el comportamiento del número de llamadas por hora se puede aproximar mediante una distribución de Poisson.
a) En un lapso de 30 minutos, ¿cuántas llamadas de emergencia se espera recibir?
b) En un lapso de 30 minutos, ¿cuál es la probabilidad de que no se registre llamadas?
c) ¿Cuál es la probabilidad de que haya más de 3 llamadas en 30 minutos?

25. El número promedio de radios que una casa comercial vende por día sigue una distribución de Poisson con una media de 1.5. Calcule la probabilidad de que la casa venda por lo menos cuatro radios durante un período de :
a) dos días b) tres días c) cuatro días

26. Los defectos en un rollo fotográfico de color promedian 0.1 defectos por rollo y la distribución que sigue el número de defectos es de Poisson. Obtenga la probabilidad de que cualquier rollo fotográfico de color presente uno o más defectos.

27. A una construcción llegan camiones de carga a razón de 2.8 camiones por hora. Obtenga la distribución de probabilidad de tener tres o más camiones que lleguen en un lapso de a) 30 minutos b) una hora c) dos horas.

28. Si el 30% de las personas que viven en una gran ciudad son empleados del gobierno, determine la probabilidad de encontrar personas que no trabajen para el gobierno en una muestra aleatoria de 20 habitantes de dicha ciudad. ¿Cuál es la probabilidad de encontrar diez o menos en la muestra?

29. El 2% de las cartas que se envía a una ciudad no tienen los timbres postales correctos. En 400 de dichas cartas:
a) ¿Cuántos timbres incorrectos se esperaría encontrar?
b) ¿Cuál es la probabilidad de encontrar 5 o menos cartas con timbres incorrectos.

30. La probabilidad de vender un seguro de vida a personas que contesten un anuncio especial, se estima que es de 0.01. Sobre esta base, si 1000 personas contestan el anuncio, ¿cuál es la probabilidad de que
a) ninguno compre un seguro?
b) por lo menos uno compre un seguro?
c) más de 10 compren un seguro?

31. ¿En qué se diferenciarían las respuestas del ejercicio 29, si el porcentaje de cartas con timbres postales incorrectos fuera del 0.4%?

32. Una encuesta nacional reciente señaló que a las 9 p.m. del sábado, 40% de televidentes sintoniza el canal A, 30% el canal B y 30% el canal C.
a) En una muestra aleatoria de 10 televidentes, ¿cuántos se esperaría que estuvieran viendo el canal A?
b) ¿Cuál es la probabilidad de que todos estén sintonizando el canal A?
c) ¿Cuál es la probabilidad de que 4 sintonicen el canal A, 3 el B y 3 el C?

33. Durante las horas de tráfico intenso los accidentes se presentan en una zona urbana con una frecuencia de dos por hora. El periodo matutino de tráfico intenso dura una hora y 30 minutos, y el vespertino do horas.
a) En un determinado día ¿cuál es la probabilidad de que no haya accidentes durante el periodo matutino de tráfico intenso?
b) ¿Cuál es la probabilidad de que haya dos accidentes durante el periodo vespertino de tráfico intenso?
c) ¿Cuál es la probabilidad de que haya cuatro o más accidentes durante el periodo matutino de tráfico intenso?
d) En un determinado día, ¿cuál es la probabilidad de que no haya accidentes durante ambos periodos de tráfico intenso?

Distribución geométrica, de pascal y multinomial

34. Suponga que X es una variable con distribución de Pascal. Calcule la función de probabilidad para cada uno de las siguientes situaciones:
a) p = 0.2, r = 2, x = 3 b) p = 0.5, r = 3, x = 5 c) p = 0.8, r = 3, x = 5

35. Suponga que la variable aleatoria X se distribuye como una binomial negativa con parámetros p = 0.6 y r = 3.
a) Calcule la función de probabilidad p(x) para x = 6, 7, 8 y 9
b) Calcule la media y desviación estándar de X
c) Calcule μ + 2σ y μ - 2σ. Luego calcule P(μ - 2σ ≤ x ≤ μ + 2σ)

36. Si la variable aleatoria X tiene distribución geométrica con parámetro p = 0.7
a) Calcule la función de probabilidad p(x) para x = 1, 2, ... , 5
b) Calcule la media y desviación estándar de X
c) Calcule μ + 2σ y μ - 2σ. Luego calcule P(μ - 2σ ≤ x ≤ μ + 2σ)

37. La distribución de parásitos(solitarias) encontrados en varias especies de peces del litoral peruano, se define como una variable con distribución de Pascal. Suponga que el evento de interés es el hallazgo de un parásito en el sistema digestivo de la merlusa. Sea X el número de merlusas que debe muestrearse hasta encontrar una infección por parásitos. Los investigadores estiman la probabilidad de observar un pez infectado en 0.544. Use esta información para estimar las siguientes probabilidades:
a) P(X = 3) b) P(X ≤ 2) c) P(X > 2).

38. Tres tiendas de repuestos venden cierto tipo de autopartes. El vendedor A provee el 50 %, el vendedor B, el 40% y el vendedor C, el 10%. Si se seleccionan aleatoriamente 5 autopartes del suministro total y se les someten a prueba para ver si están defectuosos,
a) ¿Cuál es la probabilidad de que los 5 los haya proporcionado el vendedor A?
b) ¿Cuál es la probabilidad de que 2 sean de A, dos de B y uno de C?

39. El 30% de los alumnos de una universidad local son del primer año, 30% del segundo, 20% del tercero y 20% del cuarto año. De una lista general se toma una muestra aleatoria de 8 estudiantes. Calcule la probabilidad de que en esa muestra resulten
a) dos alumnos de cada año
b) tres del primer año, tres del segundo, dos del tercero y ninguno del cuarto

40. Una serie de ocho lámparas se conectan de tal forma que si una de ellas falla, el sistema no funcionará. Si dos lámparas fallan:
a) ¿Cuál es la probabilidad de que la primera que se inspeccione sea la que haya fallado?
b) ¿Cuál es la probabilidad de encontrar las dos que fallan si se inspeccionan cuatro de ellas?
c) ¿Cuántas lámparas se deben inspeccionar para tener un 70% de probabilidad de encontrar las dos lámparas defectuosas?

41. Siete alumnos de una determinada asignatura no ha expuesto aún su tema. El profesor debe seleccionar a dos de ellos para la exposición de hoy. Sin embargo, uno de ellos se disculpa por no estar preparado debido a problemas familiares. El profesor conviene en ello, pero no puede recordar quién es este alumno. Cuál es la probabilidad de que el alumno que se disculpó no sea escogido, suponiendo una selección aleatoria de entre los siete?

42. El diez por ciento de las plantas que se adquieren en el vivero local mueren generalmente antes de dar fruto.
a) Si se compran 10 plantas, ¿cuál es la probabilidad de que no muera más que una, antes de dar fruto?
b) ¿Cuál es el menor número de plantas que se deben comprar si se quiere tener el 95% de seguridad de que 10 ó más no morirán antes de dar fruto?

43. La probabilidad de que un solo billete de lotería sea premiado es de 1 en 1000. Si una persona desea comprar 50 billetes, ¿cuál es la probabilidad de que con ninguno gane?

44. Se sabe que los defectos en rollos de papel tapiz se aproximan mediante una distribución de Poisson con una media de 2 defectos por cada 10 metros de rollo. Si se compra la mitad de un rollo, ¿cuál será la probabilidad de encontrar más de un defecto?

45. De acuerdo con las estimaciones de una compañía de seguros, la probabilidad de que se registre un incendio en una casa es del 1% al año. La compañía llega a asegurar 400 casas
a) Si muchos de los asegurados viven en casas adyacentes, por qué invalidaría esto el uso de la distribución binomial o de Poisson?
b) Suponga que los asegurados están suficientemente separados entre casa y casa. ¿cuál es la probabilidad de que no se registren incendios? ¿Al menos uno?

46. Suponga que el 5% de las facturas de venta de una compañía presentan errores en las especificaciones del material o en los números del catálogo, si se examinan cuidadosamente una muestra de 15 facturas, cual es la probabilidad de encontrar uno o menos con estos errores?. ¿Cuántas facturas se espera encontrar con estos errores?

47. Debido a la naturaleza destructiva de la verificación del estado de una tubería a prueba de explosiones, se inspecciona una muestra de partes bastante pequeña. Si de una remesa de 20, una parte está defectuosa, ¿cuál es la probabilidad de que se encuentre ésta, si se toma una muestra de 4 partes?

48. Suponga que el 20% de los adultos que viven en una ciudad nacieron allí, que el 25% nacieron en el estado pero no en la ciudad y que el 40% nacieron en el país pero no en ese estado y que el resto nacieron fuera del país. Si se toma una muestra de cuatro adultos ¿cuál es la probabilidad de que en la muestra estén representados cada uno de los 4 casos?

49. La probabilidad de que una casa se incendie en cierta área es de 0.002. El costo del daño promedio, causado por dicho incendio es de $ 20,000. ¿Cuánto estaría dispuesto a pagar el propietario de una casa por un seguro contra incendio?

50. En una escuela superior de turismo hay 25 alumnos: 14 hombres y 11 mujeres. Cinco de ellos faltaron el jueves de la presente semana.
a) ¿Cuál es la probabilidad de que dos de los ausentes fueran alumnas?
b) ¿Cuál es la probabilidad de que no hubiera alumnas ausentes?

Siguiente sesión.