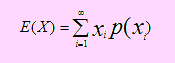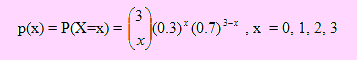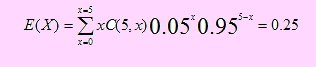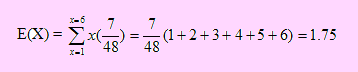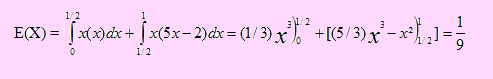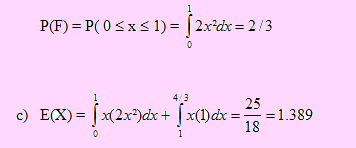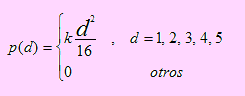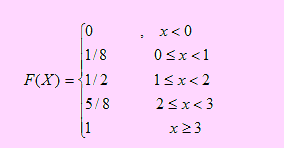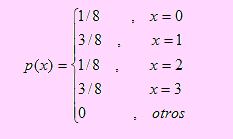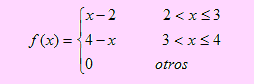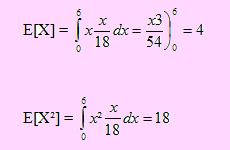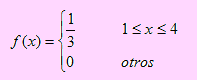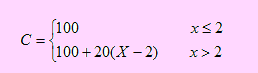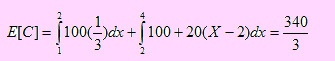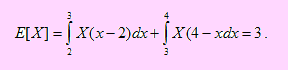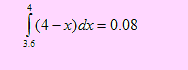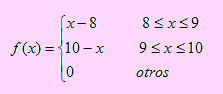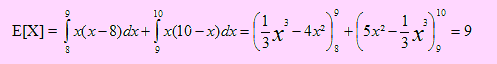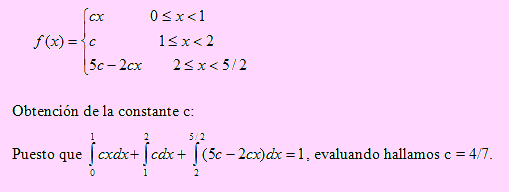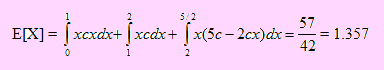4.6 VALOR ESPERADO DE UNA VARIABLE

Caso discreto

Sea X una variable aleatoria discreta cuyos valores son x1, x2, x3, ... xn , pertenecen a su espacio rango.
Sea p(x_i )=P(X = x_i ), ∀i =1, 2,..., n su función de probabilidad. Diremos que E(X) es laEsperanza Matemáticade X y se define como


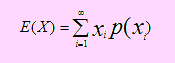
Ejemplo 51

Sea X la variable aleatoria que representa el número de caras obtenidas al lanzar una moneda 3 veces. Cuál será el número esperado de caras?

Solución

Según el Ejemplo 12 la distribución de probabilidad de X es


Podríamos decir que el número de caras que esperamos que ocurra es “una cara y media”. Otra forma de interpretarlo es: El número esperado de caras es uno o dos.

Ejemplo 52

Una agencia bancaria tiene tres cajeros automáticos. La probabilidad de que uno cualquiera de ellos falle después de un tiempo determinado de uso, es 0.1. Los cajeros operan independientemente uno de otro. En una hora determinada, cuál es el número esperado de cajeros que fallen?

Solución

La distribución del número de cajeros que fallen, resuelto anteriormente, es

 

X	0	1	2	3
p(x)	0.729	0.243	0.027	0.001

Luego el valor esperado de X es
E(X) = 0(0.729) + 1(0.243) + 2(0.027) + 3(0.001) = 0.3

Ejemplo 53

La probabilidad de que un agente vendedor realice una entrevista efectiva(realice una venta) es igual a 30%. Cierto día entrevista a 3 clientes potenciales. Si se define a X como el número de clientes que firman un contrato de venta. Cuál es el número esperado de clientes que firmen el contrato?.

Solución

La función de probabilidad al hemos hallado en el Ejemplo 22. Como esta función de probabilidad de X viene dada por

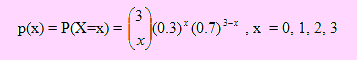
entonces, el número esperado de clientes que firmen el contrato será
E(X) = 0x(0.7)³ + 1x3x(0.3)(0.7)² + 2x3x(0.3)²(0.7) + 3x(0.3)³ = 0.9 ; es decir, el agente vendedor debe esperar que sólo uno de los tres clientes firmen el contrato.

Ejemplo 54

Una empresa ensambladora de celulares recibe tarjetas de control en lotes de 20 cada uno. El Departamento encargado de la recepción utiliza la siguiente regla de inspección: Se prueban dos tarjetas de control de cada lote. Si ninguno de ellos es defectuoso, se pasa a otro lote. Si resulta defectuoso, por lo menos uno de ellos, se prueba el lote completo. ¿Cuál es el número esperado de tarjetas de contgrol inspeccionados por lote, si se sabe por experiencia que cada lote contiene exactamente el 25% de defectuosos?

Solución

Sea X la variable aleatoria que representa el “Número de tarjetas de control inspeccionados por lote”
Como en la primera fase se prueban dos, entonces X = 2. Si por lo menos uno de ellos es defectuoso, se prueban los 20, en cuyo caso X = 20. Luego los valores de X son 2, 20. En este caso, p = 0.25 es la probabilidad de que una tarjeta sea defectuosa. Esto significa que en el lote de 20 tarjetas, habrá 5 defectuosas.
Sea A el evento “Una tarjeta de video es defectuosa”.
Si X = 2, significará que sólo se probaron dos tarjetas, esto es, que ninguna de ellas fue defectuosa, es decir, ocurrió el evento A₁’ ∩ A₂’.
Luego p(x = 2) = P(A₁’ ∩ A₂’) = C(5,0)C(15,2) / C(20, 2) = (15x14) / (20x19) = 21/38
Ahora, X = 20, significa que se encontró por lo menos una tarjeta defectuosa. Es decir,
p(x = 20) = 1 – p(x=2) = 1 – P(A₁’ A₂’ ) = 17/38
La distribución de probabilidad de X es

 

X	2	20
p(x)	21/38	17/38

Finalmente E(X) = 2(21/38) + 20(17/38) = 10.05

Ejemplo 55

Una urna contiene 4 bolas rojas, 6 negras, 8 verdes y 2 blancas. Un jugador extrae una bola de la urna. Si esta es roja, el jugador gana $ 30.00, si es negra, gana $ 20.00. Cuánto debería pagar el jugador si extrae una verde y cuando extrae una bola blanca para que el juego sea equitativo?. Además, si extrae una bola verde el jugador deberá pagar la cuarta parte de lo que pagaría si extrae una bola blanca.

Solución

Nota:
Consideraremos que un juego es equitativo si su esperanza o valor esperado del beneficio obtenido con el juego es cero.
Sea B el evento “Se extrae una bola blanca”
Sea N el evento “Se extrae una bola negra”
Sea R el evento “Se extrae una bola roja”
Sea V el evento “Se extrae una bola verde”

Sea X la variable aleatoria que representa “La ganancia del jugador”.

Si ocurre B, X = k con P(B) = 2/20
Si ocurre V, X = x/4 con P(V) = 8/20
Si ocurre R, X = $ 30 con P(R) = 4/20
Si ocurre N, X = $ 20 con P(N) = 6/20
Luego podemos formular la siguiente distribución

 

R	N	V	B
2/20	8/20	4/20	6/20
30	20	-k/4	-k

Encontremos el valor esperado
E(X) =- 30(4/20) + 20(6/20) +(-k/4)(8/20) + (-k)(2/20 = 0

De donde k = 15
Luego el jugador debe pagar $ 15.00 si extrae verde y $ 60.00 si extrae una bola blanca.

Ejemplo 56

Una empresa comercializadora de productos con valor agregado recibe lotes de 40 artículos de vestir para damas. La empresa debe realizar la última fase que es el estampado. Esta empresa acepta las prendas de vestir sabiendo que, por lo general, el lote contiene 5% de prendas defectuosas. El plan de aceptación consiste en extraer una muestra aleatoria de 5 artículos. Si se encuentra una prenda defectuosa se rechaza el lote.
a) Hallar la probabilidad de que se encuentre exactamente una prenda de vestir defectuosa en la muestra, si el lote se considera en su calidad mínima (Un lote se encuentra en su calidad máxima, si no contiene productos defectuosos).
b) ¿Cuántas prendas defectuosas espera encontrar en la muestra?

Solución

Sea X la variable aleatoria que representa “Número de prendas defectuosas en la muestra”. La probabilidad de que se extraiga una prenda defectuosa es 0.05. Si en la muestra de tamaño 5 deseamos encontrar “x” prendas defectuosas, entonces (0.05)x es la probabilidad de encontrar x defectuosas y (1 – 0.05) (5-x) es la probabilidad de que las otras “5-x” sean no defectuosas. Y como las “x” defectuosas pueden ser extraídas en cualquiera de las 5 extracciones, el número de maneras de obtener “x” defectuosas en 5 es combinaciones de 5 tomados de x en x. Todo esto nos lleva a formular la función de probabilidad de X siguiendo el modelo binomial de acuerdo a
p(x) = P(X = x) = C(5, x)0.05^x0.95^5-x,       x = 0, 1, ..., 5.
a) La probabilidad de encontrar exactamente una prenda defectuosa es
p(1) = P(X = 1) = C(5, 1)(0.05)(0.95)⁴ = 0.2036
b) El valor esperado de X, usando la definición será


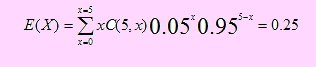
Ejemplo 57

Un conductor decide cambiar la válvula que regula el termostato de su vehículo. Para ello acude a un taller en donde el técnico dispone de cuatro válvulas, una de las cuales es el que debe usar para el vehículo en cuestión. Si las selecciona al azar una después de otra, y sin reposición, cuál es el número esperado de válvulas que ha de probar para colocar el correcto?.

Solución

Sea X el “número de pruebas que debe realizar el técnico hasta encontrar la válvula correcta”. Observe que en este caso definimos a X como el número de ensayos y no como el número de veces que debe ocurrir éxito. En el caso binomial, el número de ensayos es conocido y además los ensayos se realizan con reposición, por lo que la probabilidad de éxito no cambia. Sin embargo en este caso, las pruebas implican realizar ensayos sin reposición; por lo que la probabilidad de éxito (ubicar la válvula correcta) cambia conforme se realizan más pruebas.
Sea C el evento “Encontrar la válvula correcta”.
Si X = 1, p(1) = P(X = 1) = P(C) = ¼
Si X = 2, p(2) = P(X = 2) = P(C’  C) = (¼)(1/3)
Si X = 3, p(3) = P(X = 3) = P(C’  C’ C) = (¼)(1/3)(1/2)
Si X = 4, p(4) = P(X = 4) = P(C’  C’ C’ C) = (¼)(1/3)(1/2)(1)
Por lo que el número esperado de pruebas que debe realizarse será

E(X) = 1(1/4)+2(1/4)(1/3)+3(1/4)(1/3)(1/2)+4(1/4)(1/3)(1/2)(1) = 0.70833

Ejemplo 58

Ud. lanza una moneda tres veces. Si obtiene al menos dos caras, se le permitirá lanzar un dado y recibirá tantos soles como puntos obtenga en el dado. Qué cantidad de dinero espera ganar Ud. en este juego?.

Solución

Sea A el evento “Sale por lo menos dos caras”. P(A) = 4/8
Sea B el evento “Lanzar un dado y obtener un punto”
Sea X la variable aleatoria que representa: “Cantidad de dinero recibido”. Los valores de X son: 1, 2, 3, 4, 5, 6. La probabilidad de que salga cualquiera de las caras, digamos x, es
p(x) = P(X = x) = 1/6

El evento B ocurre sólo si ocurre A. Luego P(B) = P(A)1/6 = (4/8)x(1/6) = 4/48


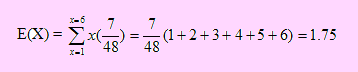
Luego espero ganar S./ 1.75.

Ejemplo 59

Todos los que participan en un determinado juego deben inscribirse pagando S./ 1.0. El juego consiste en lanzar tres argollas hacia una clavija, a la cual se ha amarrado una botella de vino. El jugador debe lanzar las argollas de uno en uno. Si ensarta una argolla gana un premio de S./ 5.0 Si logra ensartar dos argollas, gana S./ 10.0. Si logra ensartar las tres argollas, el premio es de S./ 50.0. Si suponemos que la probabilidad de ensartar en la clavija es 0.10. Cuál es la ganancia esperada del jugador, si juega a) sólo una vez. b) si juega diez veces?.

Solución

Sea X la variable que representa: “Número de argollas que logra ensartar el jugador”. Según el problema, los valores de X son: 0, 1, 2, 3.

Como la probabilidad de éxito(ensartar una argolla) es 0.1 y es constante, X es una variable que tiene distribución binomial cuya función de probabilidad viene dada por


Si se realizan diez jugadas, tendremos E(X) = 0.965 soles.

Ejemplo 60

En un determinado juego de dados, Manuel debe pagar a la mesa $ 1.0, luego del cual lanza tres dados. Manuel recibe $ 2.0 si aparece un as; recibe $ 4.0 si aparecen dos ases y $ 8.0 si aparecen tres ases. En los otros casos no recibe nada.
a) Es equitativo el juego? Justifique su respuesta
b) Si no lo fuese, cuánto debería recibir A por sacar tres ases?

Solución

Sea X la variable aleatoria definida como “Cantidad de dinero recibida por Manuel”.
Sea A el evento “Sale un as al lanzar los tres dados”
Según el problema: Si sale un as, X = 2; si sale dos ases, X = 4 y si sale tres ases, X = 8. Con las siguientes probabilidades:

X = 2 con P(X = 2) = P({(A, A’, A’), (A, A, A’), (A’, A’, A)}) = 3(1/6)(5/6)(5/6) = 75/216
X = 4 con P(X = 4) = P({(A, A, A’), (A, A’, A), (A’, A, A)}) = 3(1/6)(1/6)(5/6) = 15/216
X = 8 con P(X = 8) = P({(A, A, A)}) = (1/6)(1/6)(1/6) = 1/216

Obtención del valor esperado de X: E(X) = 2(75/216) + 4(15/216) + 8(1/216) = 218/216

a) Sin duda el juego no resulta equitativo. Para que esto ocurra E(X) debería ser $ 1.0 ya que al pagar $ 1.0 para jugar, al final no ganaría ni perdería.
b) Para que sea equitativo, debería recibir $ 6.0, si obtiene tres ases.

Ejemplo 61

Yaco decide participar en un juego que consiste en lo siguiente: Luego de firmar una boleta en blanco para participar en el juego, recibe tres bolitas para lanzarlas hacia un depósito que contiene cuatro casilleros. Gana si logra colocar dos de las bolitas en un mismo casillero. Una bolita puede caer en cualquiera de los cuatro casilleros con igual probabilidad. Yaco tiene tres oportunidades para lograr éxito. Si tiene éxito, recibe $ 219.70. Si no logra tener éxito en los tres intentos, debe pagar una determinada cantidad. Si pierde Yaco cuánto debe pagar para que el juego resulte equitativo?

Solución

Sea R el evento “En un casillero sólo caen dos bolitas”. Y sea G el evento “Gana Yaco”.
La probabilidad de que una bolita caiga en cualquiera de los cuatro casilleros es 1/4 . La probabilidad de que dos bolitas caigan en el mismo casillero es 1/16. Y que la tercera bolita no caiga en dicho casillero es 3/4 . Pero este casillero pudo haber sido cualquiera de los cuatro. Luego P(R) = 4x(1/4)(1/4)(3/4) = 4x3/64 = 3/16.

Como Yaco tiene tres intentos, Sea X la variable que representa “El número de intentos que debe hacer Yaco para ganar el juego. Según esto, Yaco gana el juego si X = 1 ó X = 2 ó X = 3. Con probabilidades
p(1) = P(X=1) = 3/16
p(2) = P(X = 2) = (13/16)(3/16) = 39/256
p(3) = P(X = 3) = (13/16)² (3/16) = 507/4096
Luego P(G) = 3/16 + 39/256 + 507/4096 = 1899/4096

El juego es equitativo si E(X) = 0. Esto significa que E(X) = 219.7(1899/4096) + k(2197/4096) = 0.
Despejando k de la ecuación, tenemos k = 189.9
Luego, si Yaco pierde deberá pagar $ 189.9 para que el juego sea equitativo.

Ejemplo 62

Un parroquiano pasado de copas llega a su casa y desea abrir la puerta de entrada. En el llavero tiene 5 llaves las que prueba una tras otra, al azar. Suponga que se encuentra suficientemente despierto como para eliminar las llaves ya probadas. Sea X la variable que representa el “número de llaves que debe probar hasta que la puerta se abra”. Hallar el número esperado de llaves que debe probar.

Solución

Sea X: Número de llaves que debe probar hasta abrir la puerta. Sea A el evento “El parroquiano logra abrir la puerta”
El siguiente esquema muestra lo que podría ocurrir.



El parroquiano logra abrir la puerta si ocurre uno de los siguientes eventos:
E , FE , FFE , FFFE , FFFFE
Esto quiere decir que X tomará valores 1, 2, 3, 4 ó 5.

Con probabilidades (1/5), (4/5)(1/4), (4/5)(3/4)(1/3), (4/5)(3/4)(2/3)(1/2) y (4/5)(3/4)(2/3)(1/2)(1), respectivamente.

La distribución de probabilidades viene dada por

 

X	1	2	3	4	5
p(x)	0.2	0.2	0.2	0.2	0.2

Luego E(X) = 1(0.2) + 2(0.2) +3(0.2) + 4(0.2) + 5(0.2) = 3

Ejemplo 63

Un fabricante de televisores utiliza cierto tipo de componente electrónico en el ensamblaje de televisores a color. Cada televisor requiere de 6 de estos componentes. Un componente defectuoso no puede ser detectado hasta que el televisor haya sido ensamblado completamente. El costo de detección, reparación y reposición de un componente defectuoso es de $ 15. El fabricante ha estado comprando estos componentes en lotes de 100 a dos proveedores diferentes. El costo por lote del proveedor A es $ 100, en tanto que del proveedor B es $ 120. Basadas en experiencias anteriores, las calidades comparadas de los lotes comprados a los dos proveedores, son los siguientes:
Proveedor A:

 

Nro estimado de componentes defectuosos por lote	1	2	3	4	5
Probabilidad	0.30	0.25	0.20	0.15	0.10

Proveedor B:

 

Nro estimado de componentes defectuosos por lote	1	2	3
Probabilidad	0.50	0.35	0.15

A qué proveedor debe comprar el fabricante dichos componentes electrónicos?

Solución

Sea X el número de componentes defectuosos encontrados en un lote.
Encontremos el número esperado de componentes defectuosos por lote para los dos proveedores:
Para el proveedor A: E(X) = 1(0.30)+2(0.25)+3(0.20)+4(0.15)+5(0.1) = 2.5
Para el proveedor B: E(X) = 1(0.50)+2(0.35)+3(0.15) = 1.5
Para una adecuada decisión calcularemos el costo total que se espera tener por lote y por cada proveedor.
Sea CT la variable que representa el Costo total esperado por lote. Según el problema
En el caso del proveedor A, CT = 100 + 15 X de donde E(CT ) = $ 100 + $ 15(2.5) = $ 137.5
En el caso del proveedor B, CT = 120 + 15 X de donde E(CT ) = $ 120 + $ 15(1.5) = $ 142.5
Sin duda el fabricante elegirá al proveedor A para que le suministre dichos componentes.

Caso continuo

Sea X una variable aleatoria continua. Sea f su función de densidad de probabilidad. Diremos que E(X) es su Esperanza Matemática y se define como

Propiedades de la esperanza de una variable
i) E(K) = K
ii) E(K + X) = K + E(X)
iii) E(KX) = KE(X)
iv) Si Y = A + BX entonces E(Y) = A + B E(X)

Nota:

Aceptaremos esto último como propiedad excusándonos del rigor ya que siendo Y = H(X) = A + BX, una función de una variable aleatoria, debiéramos haber desarrollado dicho tema. Sin embargo, lo tomaremos como válido.

Ejemplo 64

Sea X una variable aleatoria continua con función de densidad definida por

Encuentre E(X)

Solución

Usando la definición de esperanza de X, tenemos


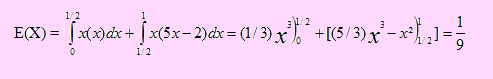
Ejemplo 66

Una máquina produce un artículo que es revisado(inspección de 100%) antes de ser despachado. El instrumento de medición es tal que es difícil leer entre 1 y 1 (datos codificados). Después que se realiza el proceso de codificación, la división medida tiene la siguiente función de densidad de probabilidad


b) Sea F el evento “El producto está fuera de la zona confusa”.
El producto está fuera de la zona confusa si la medida de su división se encuentra en el intervalo (0, 1). No se considera “fuera de la zona confusa” a los intervalos (-∞, 0) y (4/3, +∞ ) por cuanto la función de densidad es 0 en dichos intervalos.

Por ello, para saber qué fracción de los artículos caen fuera de la zona confusa, debemos calcular la probabilidad del evento F.

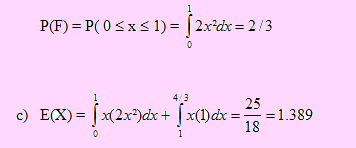
4.7 VARIANZA DE UNA VARIABLE

Sea X una variable aleatoria. Sea E(X) su valor esperado. Diremos que V(X) es la varianza de la variable aleatoria de X y la definiremos como la esperanza del cuadrado de los desvíos de la variable respecto de su valor esperado o media; es decir,

V(X)= E[(X-E(X))(Y-E(Y)) ]²

TEOREMA. Si V(X) es la varianza de la variable aleatoria X, entonces

V(X)= E(X² )- (E(X))²

Notación:

V(X) = E(X²) – μ²

Desviación estándar

Sea X una variable aleatoria. Si V(X) es la varianza de X, definimos a X como la Desviación Estándar de X tal que
σ_X= √(V(X))

Propiedades de la varianza

V(K) = 0
V(K + X) = V(X)
V(KX ) = K² V(X)
Si Y = A + BX entonces V(Y) = B²V(X)

Nota:

Hacemos la misma acotación mencionada en el caso de la esperanza de X.

Ejemplo 67

Si se lanza una moneda tres veces, cuál es el número esperado de caras que se obtendría? Con que varianza y desviación?

Solución

La función de probabilidad para X es

 

X	0	1	2	3
p(x)	1/8	3/8	3/8	1/8

Ya hemos visto que E(X) = 12/8 = 1.5
Obtención de la varianza V(X). Por el teorema V(X) = E(X²) – (E(X))²

Cálculo de E(X²):

E(X²) = 0²(1/8) + 1²(3/8) + 2²(3/8) + 3²(1/8) = 24/8 = 3
Luego V(X) = 3 – 1.5² = 0.75

La desviación estándar: σ_X = (0.75)(1/2) = 0.866

Ejemplo 68

La demanda de un determinado producto es una variable aleatoria cuya distribución de probabilidad es la siguiente:



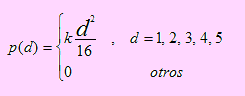
a) Hallar el valor de k
b) ¿Cuál será la demanda que se espera tener de dicho producto?
c) ¿Cuál es la desviación estándar que experimenta la demanda?

Solución

a) Para que p(x) se la función de probabilidad de X se debe cumplir


Luego
V(X) = 17.8 – 4.09² = 1.0644

De donde σ_X = 1.03173

Ejemplo 69

Sea X una variable aleatoria cuya función de distribución acumulada viene dada por



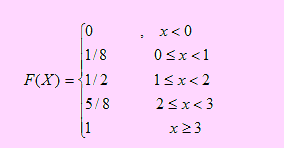
Calcule la varianza de la variable

Solución

Ante todo encontremos la función de probabilidad de X. De F podemos decir que X es una variable aleatoria discreta.

Si X < 0 entonces p(x) = 0
Si 0 ≤ x < 1 entonces p(x) = F(0) – P(X < 0) = 1/8 – 0 = 1/8
Si 1 ≤ x < 2 entonces p(x) = F(1) – P(X < 1) = 1/2 – 1/8 = 3/8
Si 2 ≤ x < 3 entonces p(x) = F(2) – P(X < 2) = 5/8 - 1/2 = 1/8
Si X ≥ 3 entonces p(x) = 1 – P( X < 3 ) = 1 – F(2) = 1 – 5/8 = 3/8

En otras palabras, la función de probabilidad de X viene dada por



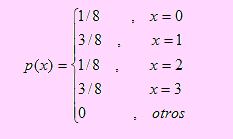
Para calcular la varianza debemos primero encontrar E(X) y E(X²):

E(X) = 0(1/8) + 1(3/8) + 2(1/8) + 3(3/8) = 1
E(X²) = 0²(1/8) + 1²(3/8) + 2²(1/8) + 3²(3/8) = 2
Luego V(X) = E(X²) – (E(X))² = 2 – 1 = 1

Coeficiente de variación

Sea X una variable aleatoria con μ_X y σ_X, su media y desviación, respectivamente. Diremos que CV(X) es el coeficiente de variación de X tal que
CV(X)= σ/μ

En términos porcentuales el coeficiente de variación mide el porcentaje de variabilidad de los valores de una variable respecto a su media esperada. Expresa el grado de dispersión de los datos alrededor de su promedio esperado.

Ejemplo 70

Una empresa dedicada a la comercialización de materiales de construcción ha establecido que la demanda de sus clientes potenciales en una nueva zona de Lima, está definida por la variable aleatoria X, en miles de unidades, con función de densidad definida por



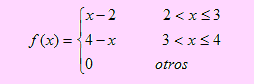
a) ¿Cuál es la demanda esperada diaria?
b) Calcule e interprete el coeficiente de variación

Solución

a) Obtención de la esperanza de X:



La demanda de materiales de construcción por los clientes potenciales de la empresa presentan un grado de dispersión relativa de 13.61%. Esto sin duda representa un margen de variabilidad muy leve.

Ejemplo 71

La media y la varianza de una variable aleatoria X son 50 y 4, respectivamente. Calcular
a) La media de X²
b) La varianza de 2X + 3
c) La desviación estándar de 2X + 3
d) La varianza de –X

Solución

De acuerdo a los datos
μ_X = E[X] = 50; &simga;_X = 4, con lo cual &simga;² = V[X] = 4
Del mismo modo, si V[X] = E[X²] – (E[X])², entonces E[X²] = 2504.
a) La media de X²:
μ_X² = E[X²] = 2504

b) La varianza de 2X + 3
Sea Y = 2X + 3. Aplicando propiedades de varianza de una variable definida como una función de otra variable ( Y = H(X)), tenemos:
V[Y] = V[2X + 3] = 2²V[X] + V[0] = 4V[X] = 4(4) = 16

c) Puesto que la desviación de una variable es la raíz cuadrada de la varianza de la variable entonces, usando el resultado del inciso anterior
σ_{(2X + 3)} = √(2X+3) = √ 16 = 4.
d) Sea Y = -X

Arreglando adecuadamente a Y, tenemos Y = (-1)X. Apliquemos ahora la propiedad de varianza de una constante por una variable (P2): V[Y] = V[(-1)X] = V[X] = 4

Ejemplo 72

Una tienda de accesorios para vehículos está rematando cierto número de artículos entre ellos un lote formado por cuatro productos al precio de $ 40.0 por todo el lote. Un comerciante puede todos los artículos en buen estado a $ 20.0 cada uno, pero todo artículo defectuoso representa una pérdida completa de $ 10.0. Basado en su amplia experiencia, el comerciante asigna probabilidades de 0.1, 0.5, 0.2, 0.1 y 0.1 a los eventos que haya 0, 1, 2, 3 y 4 artículos defectuosos en el lote, respectivamente. Si no es posible ninguna inspección, deberá comprar el lote?

Solución

Sea X la variable aleatoria que representa el “Número de artículos defectuosos en el lote”.
Según los datos, X puede tomar valores 0, 1, 2, 3, 4 con una distribución definida por

 

X	0	1	2	3	4
p(x)	0.1	0.5	0.2	0.1	0.1

Costo total de los cuatro productos: $ 40.0
Ingreso total si los cuatro productos son buenos: $ 80.0
Si por cada producto defectuoso se pierde $ 10.0, entonces 10X es el total de la pérdida.
Para responder a la pregunta definamos a Y como la ganancia obtenida al vender los cuatro productos. Según el problema, Y = 80 – (40 + 10X) = 40 – 10X. Hallemos la esperanza de Y.
Si Y = 40 – 10X entonces E[Y] = 40 – 10E[X].

Puesto que E[X] = 0(0.1) + 1(0.5) + 2(0.2) + 3(0.1) + 4(0.1) = 1.6; con lo cual E[Y] = 28.
Por tanto, el comerciante debe comprar el lote.


Ejemplo 73

Sea X una variable aleatoria cuya distribución de probabilidades es la siguiente:

 

X	0	1	2	3	4
p(x)	1/8	1/4	1/4	1/4	1/8

Calcular E[2X +1]; V[X]; V[2X + 1]

Solución

Hallaremos primero E[X] y V[X]:
E[X] = 0+1/4+2(1/4)+3(1/4)+4(1/8) = 2
V[X] = E[X²] – (E[X])² = 0+1/4+4(1/4)+9(1/4)+16(1/8) – (2)²
V[X] = 1.5

Si hacemos Y = 2X +1 entonces, aplicando propiedades
E[Y] = E[2X+1] = 2E[X] + 1 = 2(2) + 1 = 5
V[Y] = V[2X+1] = 4V[X] + 0 = 4(1.5) = 6

Ejemplo 74

Sea X una variable aleatoria con función de densidad definida por
f(x) = x/18, 0 ≤ x ≤ 6. Si Y = 10 + 2X, hallar la esperanza y la varianza de Y usando dos procedimientos diferentes.

Solución

Usaremos propiedades de esperanza y varianza para resolver el problema:
Como para hallar la esperanza y varianza de Y se requiere conocer previamente la esperanza y varianza de X, hallaremos primero estos valores: Según los datos f(x) = x/18, 0 ≤ x ≤ 6.
Con lo cual



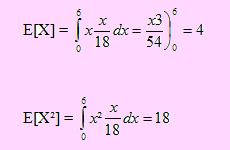
Luego V[X] = 18 – 4² = 2

Si Y = 10 + 2X entonces E[Y] = 10 + 2E[X] = 10 + 2(4) = 18.

Igualmente, V[Y] = 0 + 4V[X] = 8

Ejemplo 75

Imagina es una compañía constructora de rascacielos en el centro financiero de Lima. El suministro de estos materiales está sujeto a un tiempo de demora, digamos X, cuyo comportamiento es reflejado mediante la función de densidad f(x) = 1/3 en el intervalo de uno a cuatro días. Y f(x) = 0 si el número de días cae fuera de este intervalo.
Si el material almacenado le permite prescindir del pedido hasta por dos días, el costo de la demora se fijó en 100 soles, para cualquier demora de hasta dos días. Sin embargo, después de dos días, el costo de la demora es de 20 soles adicionales por cada día de demora. Calcular el valor esperado del costo para la compañía debido a la demora en el suministro de estos materiales?

Solución

Sea X el tiempo de demora en recibir los materiales. La función de densidad de X es



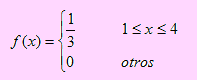
Sea C la variable que representa el costo por la demora en el suministro de los materiales. De acuerdo al problema, si x  2, entonces C = 100; pero si x > 2, entonces C = 100 + 20(X – 2) ya que por cada día adicional a los dos primeros días, se tiene un costo de 20 soles. Esto no sugiere que C puede definirse de la siguiente manera



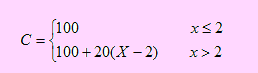
Podemos apreciar que C es una función de una variable aleatoria, por lo que, de acuerdo a los teoremas de valor esperado de una función de variable aleatoria, tenemos



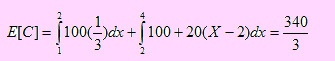
Luego, el costo esperado de demora para la compañía será de 113.33 soles.

Ejemplo 76

El tiempo X, que un cajero tarda en atender a un cliente durante las horas de mayor demanda, se distribuye exponencialmente con una función de densidad dada por f(x) = 0.2e-0.2x donde x > 0. Suponga que la media y varianza de X son 5 y 25. Si el costo que el cajero tarda en atender a cada cliente se define según la ecuación C = K X² - 5X + 8
Obtenga el valor de K si se espera tener por cliente un costo total de 83 soles

Solución

Si el costo total esperado es de 83 soles, entonces E[C] = 83. Aplicando propiedades de valor esperado a la función del costo total, tenemos
E[C] = E[KX² - 5X + 8] = K E[X²] – 5 E[X] + 8 (1)

Por otro lado, como V[X] = E[X²] – (E[X])² entonces E[X²] = V[X] + (E[X])² = 25 + 25 = 50

Reemplazando los valores conocidos en (1), tenemos 83 = K(50) – 5(5) + 8. Luego K = 2.

Ejemplo 77

Una institución benéfica decide recaudar fondos mediante la realización de un evento popular sorteando un automóvil 0 Km. Para ello se deben vender 8000 boletos a $ 5.0 cada uno. El premio consiste en la entrega al ganador de la rifa de un automóvil cuyo costo es de $ 12,000. Si una persona adquiere dos boletos, ¿cuál será la ganancia esperada de esta persona?

Solución

Sea X la ganancia esperada de una persona. Veamos qué valores toma X:

En principio la persona gasta $ 10.0 en los dos boletos de la rifa. Si ninguno de los boletos sale premiado, en cuyo caso su ganancia será 0 que recibe como premio menos lo que le costó los boletos: 0 – 10. Si uno de los boletos sale premiado, su ganancia será $ 12000 – 10; luego los valores de X son: -10 y 11990.

Encontremos ahora sus respectivas probabilidades.
X toma el valor –10 siempre que ocurre el evento P₁ ∩ P₂ , que corresponde al cuarto ramal inferior.



Observamos que la persona que compró los dos boletos puede ganar el automóvil por cualquiera de tres primeros ramales del árbol. Sólo pierde por el último. Como la ocurrencia de los eventos “Tres primeros ramales” y “El último ramal” son complementarios, entonces
p(-10) = P(X = -10) = P(P₁' ∩ P₂') = P(P₁ ∩ P₂’) P(P₁')P(P₂’/P(P₁') = 7999/8000x7998/7999 = 0.99975
p(11990) = P(X = 11990) = 1 - P(P₁’ ∩ P₂ ’) = 1- 0.99975 = 0.00025

Luego la distribución de probabilidad de X viene dada por

 

X	-10	11990
p(x)	0.99975	0.00025

Con lo cual E(X) = (-19)(0.99975) + 11990(0.00025) = -7
Se concluye que se espera que la persona pierda $ 7.0.

Ejemplo 78

Una persona desea asegurar su vehículo por un monto de $ 50,000 pagando una prima igual a K dólares. La compañía aseguradora sabe que la probabilidad de que el vehículo sufra un accidente contemplado en el contrato es 0.01. Qué prima deberá cobrar la compañía si espera ganar $1,000 dólares?.

Solución

Monto asegurado           : $ 50,000
Monto de la prima       : $ K
Probabilidad de un accidente       : 0.001
Probabilidad de que no haya accidente     : 0.991

Si X se define como       : Ganancia de la compañía de seguros
Entonces los valores de X son:
X = 50000–K siempre que ocurra un accidente; es decir P(X = 50000 – K) = 0.001
X = K siempre que no ocurra ningún accidente; es decir, P(X = K) = 0.991
La distribución de probabilidades de X es la siguiente

 

X	K - 50000	K
p(x)	0.01	0.99

Puesto que la compañía desea que E[X] = 1000, entonces
1000 = E[X] = (K - 50000)(0.01) + (K)(0.99)
Despejando K, obtenemos K = 1500. Luego la compañía aseguradora debe cobrar una prima de $ 1,500 por el yate.

Ejemplo 79

Un agente de bolsa cobra mensualmente honorarios fijos de $ 1000 más una comisión del 5% sobre el beneficio que su empresa obtiene por gestiones de consultoría que realiza. El beneficio que la empresa recibe mensualmente(en miles de dólares) se define como una variable aleatoria cuya función de densidad de probabilidad viene dada por



a) ¿Cuánto de utilidad espera obtener el consultor?
b) ¿Cuál es la probabilidad de que el consultor obtenga utilidades superiores a $ 1180?

Solución

a) Sea X la variable aleatoria que representa el beneficio que obtiene la empresa mensualmente.
Sea Y la variable que define la utilidad que obtiene mensualmente el consultor. Como éste recibe honorarios fijos de 1000 más el 5% del beneficio que es X, entonces sus utilidades mensuales se define como Y = 1000 + 0.05X . Obtendremos ahora E[Y].
Aplicando propiedades a Y, tenemos E[Y] = E[1000 + 0.05X] = 1000 + 0.05E[X].
Obtención de E[X], que representa el beneficio mensual que la empresa espera obtener.


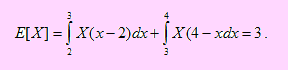
Es decir los beneficios de la empresa se espera que sean de $ 3000.
Reemplazando en E[Y], tenemos E[Y] = 1000 + 0.05(3000) = 1150
Finalmente diremos que las utilidades esperadas del consultor son de 1150 dólares mensualmente.
Utilidades del consultor superiores a $ 1180 se puede expresar como Y >1180. Luego debemos encontrar P(Y >1180). Esto es posible si pudiéramos conocer la función de densidad de Y, como no es así, usaremos el siguiente procedimiento:

P(Y >1180) = P( 1.000 + 0.05X >1.180) = P(0.05X>1.180 – 1.000) = P(X > 3.6) =


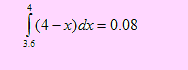
Es decir, la probabilidad de que las utilidades del consultor sean superiores a $1180 es de 0.08

Ejemplo 80

Un comerciante desea adquirir una póliza de seguro de $ 20,000 para asegurar su nueva casa asentada en un área que, de acuerdo a datos históricos, puede sufrir una pérdida total en un año, con una probabilidad de 0.001 y una pérdida parcial del 50%, con una probabilidad de 0.01. ¿Qué prima tendría que cobrar la compañía de seguros por una póliza anual para “salir a mano” con todas las pólizas de $ 20,000 de ese tipo, ignorando todas las otras pérdidas parciales?

Solución

Según los datos:
Monto de la póliza       : $ 20,000
Monto de la prima       : K
Probabilidad de una pérdida total     : 0.001
Probabilidad de una pérdida de 50%: 0.010
Sea X la variable aleatoria que representa : Ganancia de la compañía de seguros
Veamos los valores que toma X:
Si hay una pérdida total, entonces X = K – 20,000 con probabilidad igual a 0.001
Si hay una pérdida de 50%, entonces X = K – 10,000 con probabilidad igual a 0.01
Si no hay pérdida, entonces X = K, con probabilidad igual a 1 – (0.001 + 0.010)
Luego podemos construir la distribución de probabilidad de X

 

X	K - 20000	K - 10000	K
p(x)	0.001	0.010	0.989

Como por otro lado, E[X] debe ser cero para que la compañía pueda “salir a mano”, entonces
0 = E[X] = (K – 20000)(0.001) + (K – 10000)(0.010) + K(0.989)
de donde K = 120; es decir que la compañía de seguros debe cobrar una prima anual de $ 120 “para salir a mano”.

Ejemplo 81

Los accidentes registrados por una Compañía de Seguros de automóviles, aportan la siguiente información: La probabilidad de que un automovilista asegurado tenga un accidente automovilístico, es de 0.15. Si ocurre un accidente, el daño al automóvil representa el 20% de su valor en el mercado, con una probabilidad de 0.80; representa un 60% de su valor en el mercado con una probabilidad de 0.12; mientras que la probabilidad es de 0.08, si se produce una pérdida total. ¿Cuál debe ser el valor de la prima que la Compañía de seguros debe cobrar por un automóvil que vale $ 4,000 de forma tal que su ganancia esperada sea cero?

Solución

Según los datos:
Precio del automóvil             : $ 4,000
Monto de la prima           : K
Probabilidad de accidente con 20% de daño: 0.80
Probabilidad de accidente con 60% de daño: 0.12
Probabilidad de una pérdida total         : 0.08
Sea X la variable aleatoria que representa : Ganancia de la compañía de seguros
Veamos los valores que toma X:



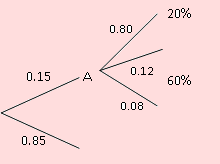
El diagrama de árbol anterior nos permite obtener los valores de X.
Como el valor del automóvil es de $ 4,000 y la prima a cobrar es K, entonces
X = K – 800, si hay un accidente con 20% de daño; es decir P(X = K –800) = 0.80x0.15
X = K – 2400, si hay un accidente con 60% de daño; es decir P(X = K –2400) = 0.12x0.15
X = K – 4000, si hay un accidente del 100% de daño; es decir P(X = K – 4000) = 0.08x0.15
X = K, si no hay accidente. Y esto ocurre con probabilidad igual a 0.85
Debemos tomar en cuenta que X toma los tres primeros valores siempre que hay un accidente, y esto ocurre con probabilidad igual a 0.15. Por ello es que hemos multiplicado por 0.15 a cada uno de estos valores.
Finalmente, como E[X] debe ser cero, entonces
0 = E[X] = (K - 800)(0.12) + (K - 2400)(0.018)+(K - 4000)(0.012)+K (0.85)
de donde K = 187.2. Luego la Compañía debe cobrar una prima de $ 187.2 para no perder ni ganar.

Ejemplo 82

Sea X una variable aleatoria que representa el peso de un artículo en onzas, cuya función de densidad viene dada por



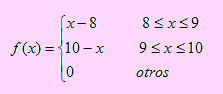
El precio de venta de cada artículo se fija en US $ 8.5. El costo de producción está relacionado al peso del artículo de acuerdo a la siguiente función de X: C = 0.5X + 2. Determine la utilidad esperada por artículo.

Solución

Sea Y la variable aleatoria que representa la utilidad por artículo.
Según los datos Y = 8.5 – C; es decir Y = 6.5 – 0.5X. Tomando valor esperado a Y, de acuerdo a las propiedades tenemos: E[Y] = 6.5 – 0.5E[X]. Según esto debemos encontrar el valor esperado del precio por artículo primero.
En efecto



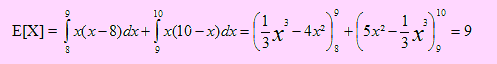
Por tanto E[Y] = 6.5 – 0.5(9) = 2. La utilidad esperada por artículo es US$ 2.0

Ejemplo 83

Una estación de gasolina recibe provisión semanalmente. Los datos recogidos en épocas pasadas sugieren que la función de densidad de probabilidad de las ventas semanales, X, medidas en miles de galones, se aproxima a la función cuya gráfica se muestra en la siguiente figura:



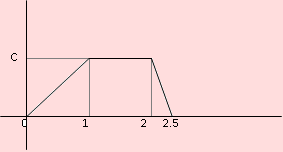
a) Encuentre el promedio de ventas semanales
b) Supongamos que el administrador de la estación tiene un sueldo básico de 1200 soles por semana. Tiene también una bonificación de 50 soles por cada millar de galones vendidos semanalmente. ¿Cuál será el ingreso total que espera tener el administrador por semana?

Solución

Obtención de la función de densidad de X.
Ecuación de L₁: y = cx
Ecuación de L₂: y = c
Ecuación de L₃: y = 5c – 2cx



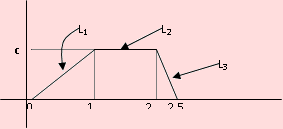
Luego la función de densidad de X, en términos de la constante c es



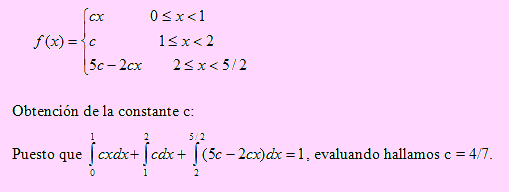
a) Obtención del promedio de ventas semanales.



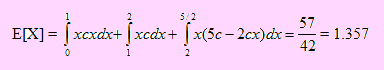
b) Si definimos a Y como la variable que representa el ingreso semanal del administrador, entonces Y = 1200 + 50X.
El ingreso total esperado es E[Y].
Esto es E[Y] = 1200 + 50E[X] = 1200 + 50(1.357) = 1267.85

Ejemplo 84

La Futura, compañía de Seguros vende una póliza de seguros a MillWard, una empresa líder en mercadeo en Europa, pero que decide expandirse al mercado latino el cual no conoce y que por lo mismo decide cubrir las posibles pérdidas en la comercialización de su nuevo producto. Si el producto no tiene salida, la compañía sufrirá una pérdida de US $ 80,000. Si el éxito que obtiene es moderado, la pérdida será de US $ 20,000. Basados en historias de mercadeo en dicha región se sabe que las probabilidades de que el producto resulte ser un completo fracaso o un éxito moderado son 0.01 y 0.05, respectivamente. Qué prima deberá cobrar la compañía de seguros por la póliza si sólo desea cubrir sus gastos, sin considerar otros tipos de posibles pérdidas?.

Solución

Definamos a X como la ganancia que la compañía de seguros obtendrá. Sea K la prima a cobrar.
Puesto que sólo desea cubrir sus gastos, entonces se debe cumplir que no debe tener ganancia; es decir, E[X] = 0.
Ahora bien,
Si el producto resulta en un completo fracaso, X = K – 80,000 con probabilidad 0.01
Si el producto resulta con éxito moderado, X = K – 20,000 con probabilidad 0.05
Pero si no hay pérdida, entonces X = K; esto ocurre con probabilidad 1 – (0.01 + 0.05) = 0.85
Luego E[X] = (K-80000)(0.01) + (k-20000)(0.05) + K(0.85) = 0
De donde se tiene K – 1800 = 0. Por tanto la compañía de seguros debe cobrar una prima de US $ 1800 si sólo desea cubrir sus gastos.

Siguiente sesión.