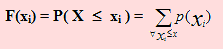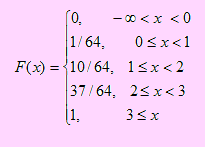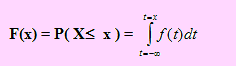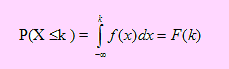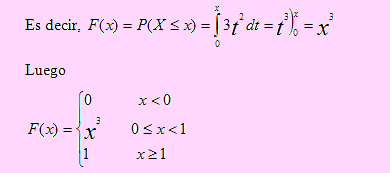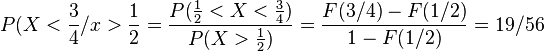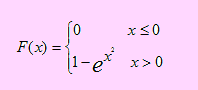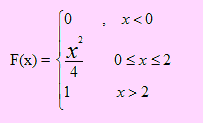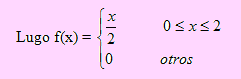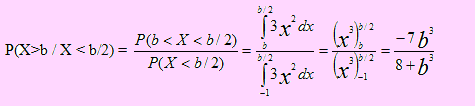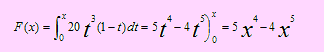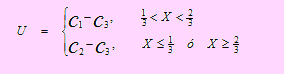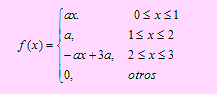4.4 FUNCIÓN DE DISTRIBUCIÓN ACUMULADA

Caso discreto
Si X es una variable aleatoria discreta, para un valor xi de X, F(x_i) se define como



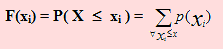
Propiedad 1:

0 ≤ F(x) ≤ 1, ∀ x εR, ya que F(x) es una función de probabilidad para todo valor de X = x del espacio rango de la variable. Y según sabemos, las funciones de probabilidades están limitadas entre 0 y 1.
Propiedad 2:

F(x) es una función no decreciente. Esto significa que si x₁ < x₂ , entonces F(x₁ ) ≤ F( x₂).
Propiedad 3:

F(œ ) = P(X < œ ) = 1. Y esto es cierto ya que el evento “X < œ “ incluye todos los valores posibles de X en su espacio rango.

F(- œ ) = P(X < - œ ) = 0. Contrario al caso anterior, el evento “X < -œ “ es un evento imposible por cuanto suponemos (y estamos convencidos) que no valores de X anteriores a -. Lo que implica que F(-œ) = P(X < -œ ) = P(œ ) = 0.

Propiedad 4

Sean x_k , x_k+1 ε R_X . Sea x ε R_X / x_k ≤ x < x_k+1 entonces F(x) = F(x_k ). Esto implica que F(x) es constante (gráficamente es un segmento horizontal) en todo el mencionado intervalo [x_k , x_k+1 ).

Propiedad 5

Si X es una variable aleatoria discreta, entonces
a) P( a ≤ x ≤ b ) = P( X ≤ b ) – P(X ≤ a) + P(X = a) = F(b) – F(a) + p(a)
Esto se puede verificar simplemente observando el siguiente esquema



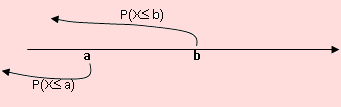
Al restar P(X ≤ a) de P(X ≤ b), estamos restando P(X = a); como se pide la probabilidad en el intervalo donde se incluye a, entonces se debe sumar p(a). Similar explicación puede darse a los siguientes casos

b) P( a < X ≤ b ) = P(X ≤ b ) – P( X ≤ a) = F(b) – F(a)
c) P( a ≤ X < b ) = P(X ≤ b) – P(X ≤ a ) + P(X = a) – P(X = b) = F(b) - F(a) + p(a) - p(b)
d) P( a < X < b) = P(X ≤ b ) – P(X ≤ a) – P(X = b) = F(b) – F(a) – p(b)

Ejemplo 39

Sea X una variable aleatoria discreta. cuya función de probabilidad viene definida en la siguiente tabla:



Luego la función distribución acumulada, presentada de manera formal, es



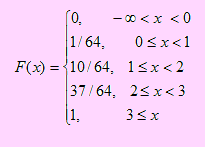
Ejemplo 40

Se lanza al aire una moneda tres veces. Supongamos que se define la variable aleatoria X como X = nc – ns, donde ns representa el número de caras y ns representa el número de sellos obtenidos.
a) Encuentre el espacio muestral Ω
b) Obtenga el espacio rango de X, R_X.
c) Obtenga la distribución de probabilidad de X
d) Obtenga la distribución acumulada de X
e) Construya la gráfica de p(x) y F(x).

Solución

a) Los elementos de Ω son Ω = { SSS, SSC, SCS, CSS, SCC, CSC, CCS, CCC }
b) Puesto que al lanzar la moneda tres veces el número de caras,nc y ns el número de sellos puede variar de 0 a 3, entonces nc - ns = {-3, -1, 1, 3 }, por lo que
X toma los valores -3, -1, 1, 3; con lo cual R_X = { -3, -1, 1, 3 }
c) Daremos la siguiente explicación para encontrar p(x):
X = -3 si se obtiene 0 caras; es decir p(-3) = 1/8
X = -1 si se obtiene una cara y dos sellos, por lo que p(-1) = 3/8
X = 1 si se obtiene dos caras y un sello, por lo que p(1) = 3/8
X = 3 si se obtiene tres caras y cero sellos, por lo que p(3) = 1/8
Luego

 

X	-3	-1	1	3
p(x)	1/8	3/8	3/8	1/8

d) Para obtener F(x), consideraremos los siguientes casos:





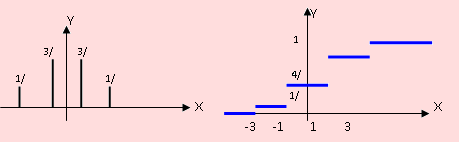
La gráfica de las dos funciones p(x) y F(x) se muestra en las figuras anteriores Caso continuo:

Si X es una variable aleatoria continua, la función de distribución acumulada de X, F(x), se define como



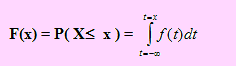
Observaciones

a) Si bien la evaluación y obtención de F en el caso discreto se presta a muchas operaciones engorrosas de cálculo, en el caso continuo el problema se convierte en utilizar adecuadamente los criterios matemáticos de integración(lo que en muchos casos también puede ser engorroso).
b) A diferencia del caso discreto donde P(X < k )=P( X ≤ k ) – P(X = k) = F(k) – p(k)
Si la variable aleatoria X es continua P(X < k ) = P( X ≤ k ). Y esto se demuestra matemáticamente ya que siendo



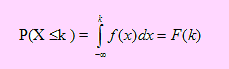
Evaluemos ahora la probabilidad del evento { X < k }.



Teorema

Si X es una variable aleatoria continua en el intervalo (a, b) y F es su función de distribución acumulada entonces P( a ≤ X ≤ b ) = F(b) – F(a)
Obtención de la función de distribución de probabilidad a partir de la distribución acumulada de la variable X.

Caso discreto:

Sea X una variable aleatoria discreta con valores posibles x₁, x₂, …, x_n, x_n+1, … . Si F es la función de distribución acumulada de X, entonces
p(x_i) = P( X = x_i) = F(x_i) – F(x_i-1) Esto es cierto ya que p(x_i) = P( X = x_i) = P(X ≤ x_i) – P(X < x_i)
= F(x_i) – P(X ≤ x_i-1 ) = F(x_i) - F(x_i-1)

El siguiente ejemplo nos exime de mayores explicaciones:

Sea X una variable aleatoria discreta cuya función de probabilidad está dada por

 

X	0	1	2	3
p(x)	0.40	0.20	0.25	0.15

F(2) = P(X ≤ 2) = p(0) + p(1) + p(2)
F(1) = P(X ≤ 1) = p(0) + p(1)
Restando miembro a miembro y cambiándolos, tenemos: p(2) = F(2) – F(1)

Caso continuo:

Sea X una variable aleatoria continua con f su función de densidad de probabilidad.



a) Obtener la función de distribución acumulada de X
b) Usando F, obtener P(X < 1/2 )
c) Si se sabe que X es mayor que 1/2 , cuál es la probabilidad de que sea menor que3/4 ? Use F para evaluar esta probabilidad.

Solución

a) Por definición F(x) = P(X ≤ x )



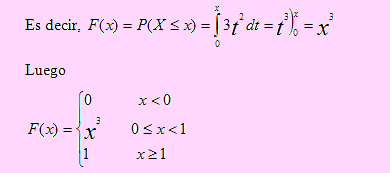
b) Como X es una variable continua F(1/2) = P(X  1/2)= P(X < 1/2)=1/8
c) Se nos pide evaluar la probabilidad condicional del evento {X < ¾} dado el evento {X<1/2). Es decir



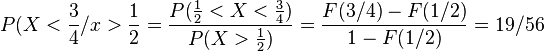
Ejemplo 42

Los gastos de viajes semanales (en miles de dólares) que el personal de ventas de la Empresa TORA, justifica cada semana, es una variable aleatoria cuya función de distribución acumulada está dada por



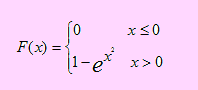
a) Qué porcentaje de vendedores gastan semanalmente menos de 500 dólares?
b) El tirano del jefe ha ofrecido unas vacaciones de dos semanas a quien justifique gastos que se encuentren en el 15% inferior. Si Ud. ha gastado 312 dólares, conseguirá unas vacaciones?
c) Obtenga la función de densidad de probabilidad de X

Solución

a) Usemos la función de distribución acumulada F.
P(X < 1/2 ) = P(X  1/2 ) = F(1/2) = 1 – e-0.25 = 0.2212
Luego, aproximadamente el 22% de los vendedores gastan menos de $ 500 semanalmente

b) Hallaremos la probabilidad de que X sea menor que 0.312. Si este valor es menor a 0.15, entonces diremos que podemos obtener dichas vacaciones.
P(X < 0.312) = P(X ≤ 0.312 ) = F(0.312) = 0.092756. Como el 9.28% han gastado menos de $ 312, entonces sí puedo obtener unas vacaciones por estar por debajo del 15% inferior.
c) Para hallar la función de densidad de probabilidad de X debemos derivar a F.

En efecto, derivando a F(x), respecto a x, encontramos f(x) = -2x e^-x2,       x ≥ 0.

Ejemplo 43

La variable aleatoria continua X tiene por función de densidad de probabilidad a



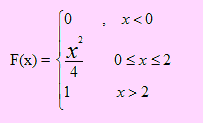
Si se hacen dos determinaciones independientes de X.

a) Encuentre la función de densidad de probabilidad de X

Usando la función de distribución acumulada F, resuelva las siguientes preguntas:

b) Cuál es la probabilidad de que ambas determinaciones sean mayores que uno?.
c) Si se han hecho tres determinaciones independientes, cuál es la probabilidad de que exactamente dos sean mayores que uno?

Solución

a) De acuerdo al Teorema, para encontrar la función de densidad f debemos derivar respecto a x.
Si X < 0 , entonces f(x) = 0
Si 0 ≤ X ≤2 , entonces f(x) = x/2
Si x > 2, entonces f(x) = 0



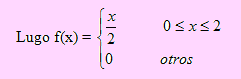
b) Sea A el evento {x/x >1} definido como la primera determinación
Sea B el evento {x/x >1} definido como la primera determinación

Sabemos que F(x) = x²/4 , 0  x  2.
Entonces
P(A) = P({x/x >1}) = P(X > 1) = 1 - P(X ≤ 1) = 1 - F(1) = 1 - 1/4 = 0.75

Como P(A) = P(B), tenemos P(A ∩ B) = (3/4)(3/4) = 9/16

c) Ahora se sabe que se realizaron tres determinaciones. Queremos que, exactamente dos de ellas sean mayores que uno.

Debemos definir otra variable que represente el número de determinaciones que cumplan dicha condición. Sea Y la variable aleatoria definida como el “Número de determinaciones que son mayores que uno”.

Según esto, Y es una variable aleatoria discreta que toma valores 0, 1, 2 y 3. Si de un total de tres determinaciones, queremos encontrar la probabilidad de que dos de ellas cumplan con la condición de ser mayores que uno, podemos usar el modelo binomial para resolverlo.

Afirmamos que Y es una variable binomial por cuanto se tiene n = 3 elecciones(determinaciones), cada uno de los cuales son independientes uno de otro. La probabilidad de éxito p = P(X>1) = ¾, encontrado en b).

Luego la función de probabilidad para Y = 2, usando un razonamiento dado en dos ejemplos anteriores de variable discreta será:
P(Y = 2 ) = C(3, 2)(3/4)²(1/4) = 27/64

Ejemplo 44

Sea X la demanda de un producto en tiempos de recesión. Estudios anteriores han demostrado que el comportamiento de X se puede expresar mediante la siguiente función
f(x) = be^-bx,     x > 0
Sea p_j = P(j ≤ X < j + 1).
a) Demuestre que, ∀ b, b>0, f es la función de densidad de probabilidad de X
b) Demuestre que pj es de la forma (1 – a )aj y determine a.

Solución

a) f será la función de densidad de probabilidad de X si se cumple que



Ejemplo 45

La variable aleatoria continua X tiene por función de densidad de probabilidad a
f(x) = 3x²     -1 ≤ x ≤ 0. Si “b” es un número que satisface –1 < b < 0, calcule la probabilidad P(X>b / X < b/2)

Solución



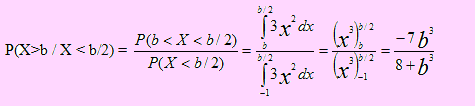
Ejemplo 46

Supongamos que f y g son dos funciones de densidad de probabilidad en el mismo intervalo, a ≤ x ≤ b.

a) Demuestre que f + g no es una función de densidad de probabilidad en el intervalo a ≤ x ≤ b.
b) Demuestre que, ∀ β con 0 <β< 1, βf(x) + (1- β)g(x) es una función de densidad de probabilidad en ese intervalo.

Solución

a) Las dos condiciones que deben cumplirse para que una función tal como f sea una función de densidad de probabilidad de alguna variable tal como X, son



Como se cumple la segunda condición, entonces h(x) = βf(x) + (1-β)g(x) es una función de densidad de probabilidad sobre el intervalo a ≤ x ≤ b.

Ejemplo 47

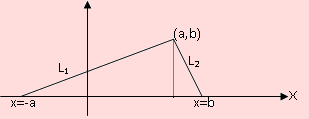
Supongamos que la gráfica que se muestra en la siguiente figura representa la función de densidad de probabilidad de una variable aleatoria X. Cuál es la relación entre “a” y “b”?



Solución

Encontremos la definición de f según la gráfica. La función f está formada por las rectas L₁ y L₂


Ejemplo 48

El porcentaje de alcohol (100X) en cierto compuesto puede ser considerada como una variable aleatoria, en donde X, 0 < X < 1, tiene la siguiente función de densidad:

f(x) = 20x³(1-x),       0 < x < 1.
a) Encuentre una expresión para la función de distribució acumulada de X grafíquela.
b) Calcular P(X ≤ 2/3)
c) Supóngase que el precio de venta del compuesto anterior depende del contenido de alcohol. Específicamente, si el compuesto se vende en C1 dólares/galón, de otro modo, se vende en C2 dólares/galón. Si el costo es C3 dólares/galón, encuentre la distribución de probabilidad de la utilidad neta por galón y obtenga una expresión para la utilidad esperada.

Solución

a) Si f(x) = 20x³(1-x),     0 < x < 1,   entonces, por definición de F, tenemos

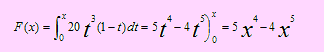
la gráfica de esta función se muestra en la siguiente figura:



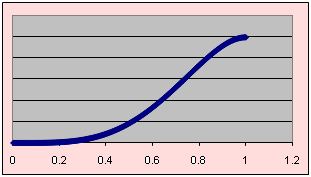
b) Usando la distribución acumulada P(X ≤ 2/3) = F(2/3) = 5(2/3)⁴ - 4(2/3)⁵ = 0.46090535
c) Sea U la variable aleatoria definida como la utilidad neta por galón. Según el problema,
Si 1/3 < X < 2/3 entonces U = C₁ en caso contrario, U = C₂ dólares/galón. De acuerdo a esto y sabiendo que el costo es C₃ dólares/galón, diremos que la utilidad neta por galón U, tiene por función de distribución a


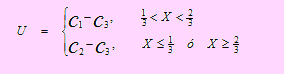
Calculemos ahora el valor esperado de U. Por definición
E[U] = (C₁ - C₃ )P(1/3 < X < 2/3) + (C₂ - C₃)( P(X ≤ 1/3) + P(X ≥ 2/3))
E[U] = (C₁ - C₃ )(F(2/3) - F(1/3))+ (C₂ - C₃ )(F(1/3) + (1 - F(2/3))
E[U] = (C₁ + C₂ )(0.46091) + (C₂ - C₁ )(0.04527)

Ejemplo 49

Sea X una variable aleatoria continua con función de densidad definida por



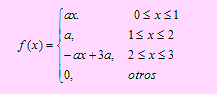
Solución



c) Sea A el evento “X_i es mayor que 3/2, i = 1, 2, 3”
P(A) = P(X₁ >3/2 ∩ X₂ >3/2 ∩ X₃ >3/2 )

Puesto que los X_i son variables independientes entonces

P(X>X₁ ) = P(X>X₂ ) = P(X>X₃ )
Por lo que P(A) = (P(X > 3/2))³ = 1/8

Ejemplo 50

Supongamos que el diámetro de un cable eléctrico, digamos X, es una variable aleatoria continua con su función de densidad es f(x) = 6x(1-x) , 0 ≤ x ≤ 1.

a) Verifique que f es efectivamente la función de densidad de probabilidad de X
b) Obtener una expresión para F, la distribución acumulada de X
c) Determinar un número b tal que P( X < b ) = 2 P(X > b)
d) Calcular P(X ≤ 1/2 / 1/3 < X < 2/3 ).

Solución

4.4 EJEMPLOS PROPUESTOS

Tres egresados tienen entrevistas programadas para empleo durante las vacaciones en el Montero Mark. El resultado de cada entrevista es Obtener el empleo o no obtenerlo.
a) Haga una lista de los resultados obtenidos.
b) Defina una variable aleatoria que represente la cantidad de ofertas hechas. Es una variable aleatoria discreta o continua?
c) Indique el valor de la variable aleatoria para cada uno de los casos.

2. La tasa de interés de préstamos otorgados por las entidades financieras de la ciudad se encuentra muy diferenciada. Suponga que la variable aleatoria de interés es la cantidad de instituciones crediticias de este grupo que ofrecen una tasa fija a 30 años, de 8,5% o menos. ¿Qué valores puede asumir esta variable aleatoria?

3. YacoBas es un técnico en laboratorio y diariamente debe realizar diversos tipos de análisis de sangre para el cual debe seguir uno de dos procedimientos. El primero requiere uno o dos pasos separados, y el segundo puede requerir uno, dos o tres pasos.

Haga una lista de los resultados experimentales asociados con la ejecución de un análisis.Si la variable aleatoria de interés es la cantidad de pasos requeridos para terminar el análisis, indique qué valor asumirá la variable aleatoria en cada uno de los resultados experimentales.

4. En un juego de póker una mano de cartas puede contener de cero a cuatro ases. Si X es la variable aleatoria que denota el número de ases, enumere el espacio rango de X. ¿Cuáles son las probabilidades asociadas con cada valor posible de X?

5. El encargado de un almacén de ropa de mujeres está interesado en el inventario de polos, que en ese momento es de 30(todas las tallas). El número de polos vendidos desde ahora hasta el final de la temporada se distribuye como
f(x) = e^-2020^x/x!,       x = 0, 1, 2, ...
Encuentre la probabilidad de que le queden polos sin vender al final de la temporada.

6. Una variable aleatoria X tiene por función de distribución acumulada F(x) = 1 - (1/2)^(x+1),       x = 0, 1, 2, ...

a) Determine la función de densidad de probabilidad de X
b) Encuentre P(0 < X ≤ 8 )

7. Dada las siguientes funciones de densidad de probabilidad de X,
a) encuentre el valor de la constante k para que f sea la función de densidad de probabilidad de X
b) Encuentre la función de distribución acumulativa de X


Siguiente sesión.