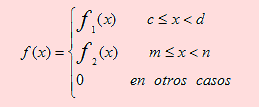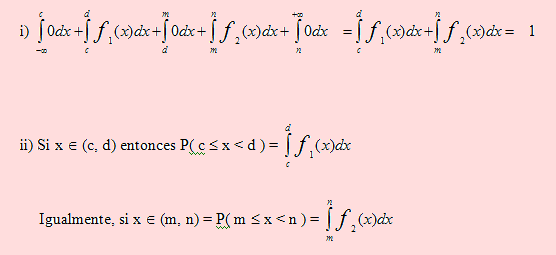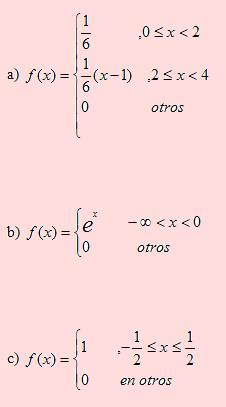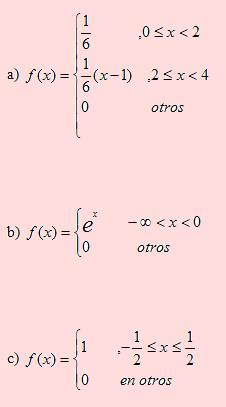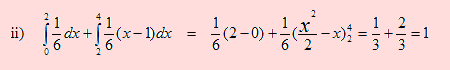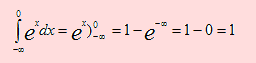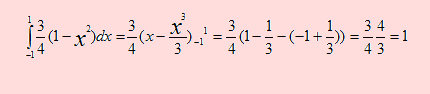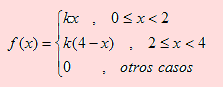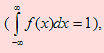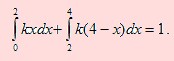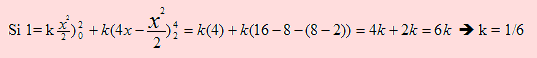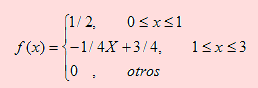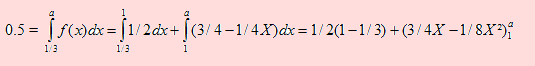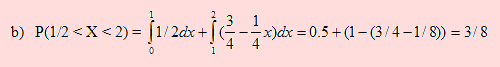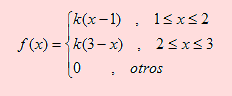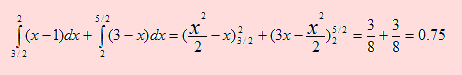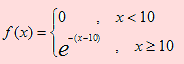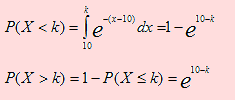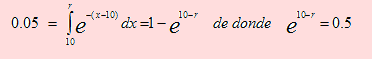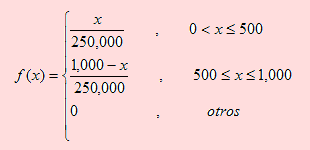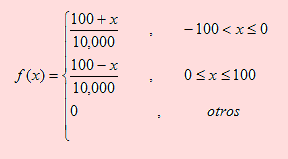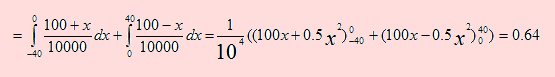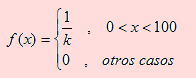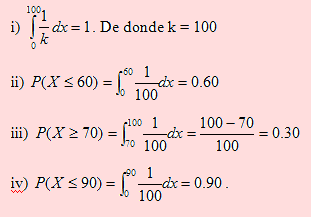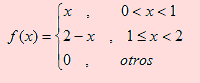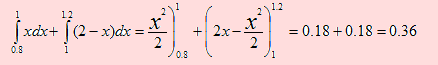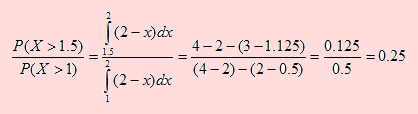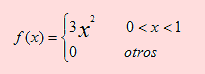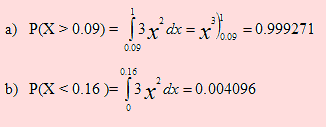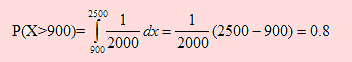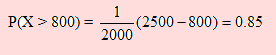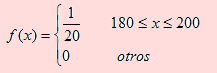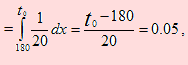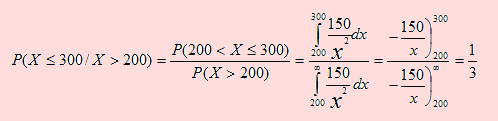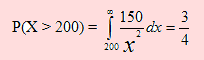4.3 VARIABLES ALEATORIAS CONTINUAS
Función de densidad de probabilidad de una variable continua
Sea Ω el espacio muestral asociado al experimento ζ. Sea X una variable aleatoria. Diremos que X es una variable aleatoria continua si existe una función f a la cual llamaremos función de densidad de probabilidad de X, que satisface las siguientes condiciones:

Observaciones
La gráfica de la función de densidad de probabilidad de X se muestra en la siguiente figura.
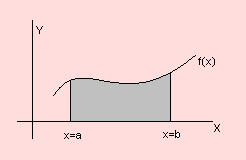
1. En el caso de las variables aleatorias discretas la gráfica de la función de probabilidad son barras verticales cuyo valor probabilístico viene determinado por la altura de dichas barras.
En el caso continuo la gráfica de la función de densidad es una curva y las probabilidades de que X esté en un intervalo (a, b) ó a ≤ x ≤ b, es el área de la región formada por la curva y las rectas x = a y x = b, como se muestra en la figura anterior.
2. En el caso de las variables discretas existe p(xi) ≥ 0, por lo que P(X = x i) ≥ 0. Sin embargo, en el caso continuo se tiene que P(X = xi) = 0. Por ello, podemos concluir, sin mayores detalles matemáticos que
P(a ≤ x ≤ b ) = P(a ≤ x < b ) + P(X = b) = P(a ≤ x < b)+0
Luego,
P(a ≤ x ≤ b ) = P(a ≤ x < b ) = P(a < x ≤ b) = P(a < x < b)
Si X es una variable aleatoria continua cuyo espacio rango es el intervalo ( α , β ) y f es su función de densidad de probabilidad, entonces
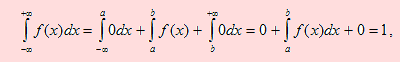 ,
,
por las condiciones para que f sea una función de densidad de probabilidad.
3. Por otro lado, si X es una variable aleatoria cuya función de densidad viene dada por
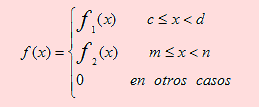
entonces
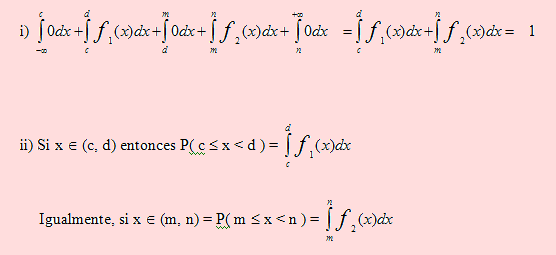
Ejemplo 26
Verifique si las siguientes son funciones de densidad de probabilidad de X
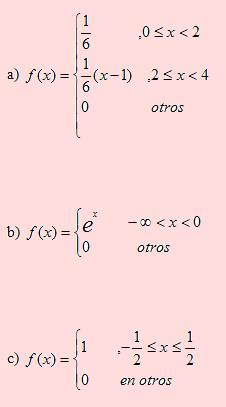
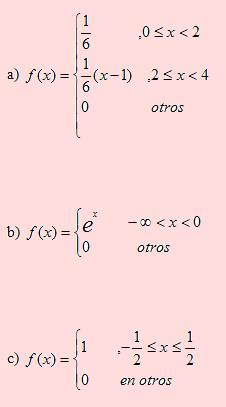
Solución
a) Para que f sea función de densidad de probabilidad de X, se debe cumplir que
i) f(x) ≥ 0. En efecto, para cualquier valor de x en los intervalos dados, f(x) ≥ 0
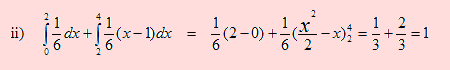
b). En este caso, si -œ < x < 0 entonces e -œ < e x < e0 de donde 0 < f(x) < 1.
Ahora vamos a verificar si se cumple la segunda condición
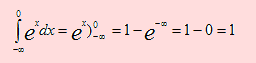
Luego f es una función de densidad de X
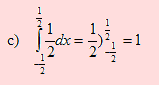
d) En este caso tenemos
Si –1 ≤ x ≤ 1 entonces –1 ≤ -x3 ≤ 1. Sumando uno a la desigualdad, tenemos 0 ≤ 1- x3 ≤ 2 de donde 0 ≤ ¾(1- x3 ) ≤ 6/4, que satisface a la primera condición
Igualmente
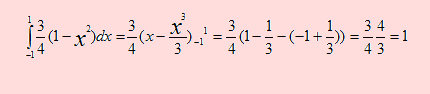
Ejemplo 27
Considere la siguiente función
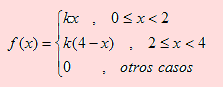
Hallar un valor de k para que f sea una función de densidad de probabilidad
Solución
Usando la segunda condición
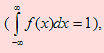
se debe cumplir que
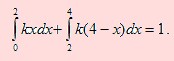
Desarrollando la expresión del primer miembro, tenemos
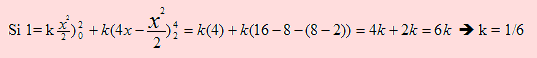
Suponga que X es una variable aleatoria cuya función de densidad está representada por la siguiente figura
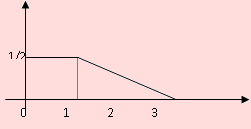
a) Si P(1/3 ≤ x ≤ a) = 1/2, determinar el valor de a
b) Calcule P(1/2 < x < 2)
Solución
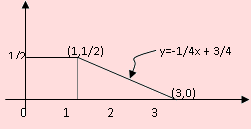
Las ecuaciones de las rectas que definen a la función de densidad son:
L1: y = 1/2;
L2: y = -1/4x + 3/4
Por ello, la función de densidad viene dada por
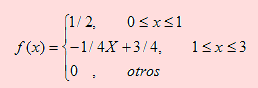
(Nota: Se puede verificar que f es una función de densidad. Dejamos esto para el lector)
a) P( 1/3 ≤ x ≤ a ) = 1/3 significa que
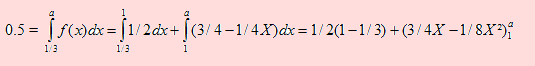
Efectuando y simplificando tenemos:
12 = 8 + 18a - 3a2 - 15. Las soluciones son: -0.91578 y -6.91578.
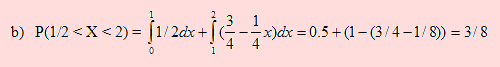
Ejemplo 29
Una estación gasolinera recibe provisión semanalmente. Las estadísticas anteriores sugieren que la función de densidad de probabilidad de las ventas semanales X, medidas en miles de galones, se aproxima a la función cuya gráfica se muestra en la siguiente figura
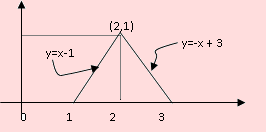
a) Obtenga la función de densidad de X
b) Evalúe P(3/2 < X < 5/2 )
Solución
a) Sea f la función de densidad de X. Según la gráfica, f se define de la siguiente manera:
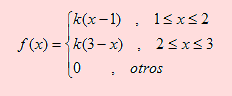

Por otro lado, es fácil verificar que f(x) ≥ 0 para todo valor de x
b) Encontrar P(3/2 < X < 5/2 ) significa trabajar con las dos definiciones de f ya que el intervalo cae dentro de los dos.
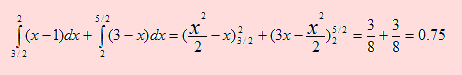
Ejemplo 30
Sea X una variable aleatoria cuya función de densidad viene dada por
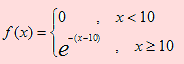
a) Hallar el valor de k tal que X sea igualmente probable de ser mayor que k o menor que k.
b) Encuentre el valor de r tal que la probabilidad de que X sea menor que r sea igual a 0.05.
Solución
a) De acuerdo a los datos se debe cumplir que P(X > k ) = P(X < k).
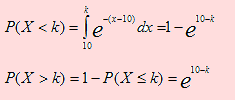
Igualando ambos términos, obtenemos 2e10-k = 0.5; de donde k = 10.69
b) P(X < r ) = 0.05 implica que
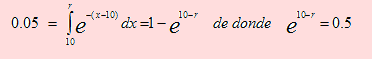
Tomando logaritmo neperiano tenemos 10 – r = Ln(0.5) . Luego r = 10.69
Ejemplo 31
Supongamos que la variable aleatoria X representa la resistencia al corte de ensayos de punto de soldadura, cuya función de densidad de probabilidad viene dada por
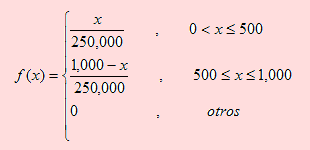
Determinar el valor de a y b tal que P(X < a ) = 0.50 y P(X < b ) = 0.90.
Solución
Para hallar el valor de a será suficiente suponer que pertenece al intervalo (0, 500). Según esto, P(X < a ) = 0.5 implica que

Ejemplo 32
Una misilera antiaérea lleva tres misiles que deben ser disparados contra una línea férrea que se extiende paralela a la costa. Si un misil cae a menos de 40 metros de la vía, ésta quedará suficientemente destruida impidiendo el flujo normal de los trenes. La densidad de impacto de un proyectil viene dada por la función
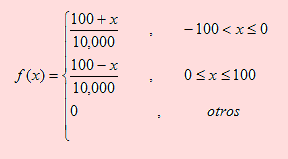
Solución
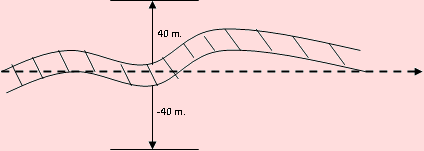
El esquema anterior muestra la situación que debe ocurrir para que la vía quede lo suficientemente dañada para quedar inutilizada.
Los misiles deben caer dentro de los intervalos (-40, 0) y (0, 40).
Esto implica que, si X se define como “La distancia entre el punto donde cae el misil y la vía”, la distancia es | X-40 | > 0.
La probabilidad de que esto ocurra es P( | X-40 | > 0) = 1 – P(| X-40 | ≤ 0) = 1 - P( -40 ≤ X ≤ 40 ).
Evaluemos P( -40 ≤ X ≤ 40 ):
P( -40 ≤ X ≤ 40 ) = P( -40 ≤, X ≤ 0 ) + P( 0 ≤ X ≤ 40 ) =
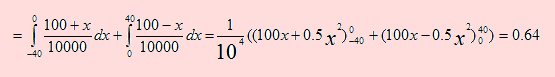
Ejemplo 33
El tiempo (en días) que una empresa constructora tarda en colocar los cimientos de un moderno edificio de 500 metros cuadrados, se define como una variable aleatoria continua cuya función de densidad de probabilidad viene dada por
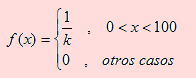
i) Hallar el valor de k para que f sea reconocida como una función de densidad de X
ii) Cuál es la probabilidad de que el tiempo máximo requerido sea de 60 días.
iii) Cuál es la probabilidad de que se tarde por lo menos 70 días?
iv) Según el proyecto la empresa constructora está obligada a completar el 80% de los cimientos en 90 días. Cumple la empresa con el proyecto?
Solución
Usando la segunda condición para que f sea f.d.p. de X, tenemos
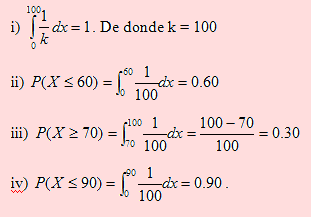
Esto significa que el 90% de los cimientos serán completados hasta los 90 días. Luego la empresa sí está cumpliendo con el proyecto.
Ejemplo 34
Una gasolinera tiene dos bombas que pueden bombear cada una hasta 10 mil galones de gasolina por mes. La cantidad total de gasolina bombeada en un mes es una variable aleatoria X (expresada en unidades de diez mil galones), con una función de densidad de probabilidad dada por
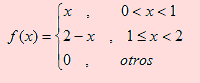
a) Calcule la probabilidad de que la gasolinera bombee entre 8000 y 12000 galones en un mes
b) Si se sabe que la gasolinera ha bombeado más de 10000 galones en mes en particular, cuál es la probabilidad de que haya bombeado más de 15000 galones durante un mes?
Solución
Sea X: Cantidad de gasolina bombeada en un mes(en unidades de diez mil)
a) P(0.8 ≤ X ≤ 1.2) =
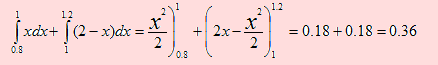
b) Esta es una probabilidad condicional donde el evento “X>1.0000” ya ha ocurrido y se debe encontrar la probabilidad del evento “X > 1.5000”. Es decir, debemos encontrar
P(X>1.5 / X > 1 ) =
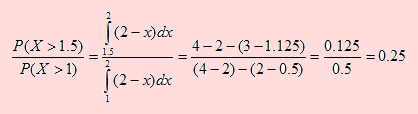
Ejemplo 35
La tasa principal de interés en el sistema financiero, predicho para el mes de Enero de 2010, fue considerada una variable aleatoria por la coyuntura del momento. Según los analistas, su función de densidad de probabilidad está dada por
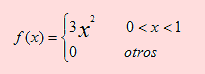
Si se selecciona aleatoriamente a un analista
a) Cuál es la probabilidad de que la predicción respecto a la tasa de interés sea mayor que 9%?
b) Cuál es la probabilidad de que la predicción sea menor que 16%?
Solución
Sea X la variable aleatoria definida como “Valor de la tasa de interés predicha por un analista”
Según esto
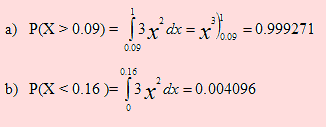
Ejemplo 36
a) En un día dado, cuál es la probabilidad de que las ventas excedan 900 dólares?
b) El restaurante requiere ventas diarias de por lo menos 800 dólares para cubrir sus gastos, cuál es la probabilidad de que en un día dado el establecimiento no cubra los gastos?
Solución
a) De acuerdo a la definición de la variable aleatoria X debemos hallar P(X > 900).
En efecto
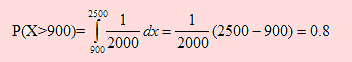
b) Para ver si cubre o no sus gastos debemos encontrar P(X > 800). Si el valor de esta probabilidad es bastante alta(digamos 0.8 o más) diremos que es muy probable que cubra sus gastos, de otra manera no lo hará.
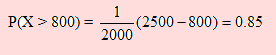
Podemos afirmar con cierto grado de confianza que probablemente cubra sus gastos.
Ejemplo 37
Debido a la eficiente labor de publicidad desarrollada por una aerolínea de bandera nacional, la demanda de clientes se ha incrementado considerablemente a tal punto que la gerencia de operaciones se encuentra preocupada por el tiempo de vuelo entre Lima y el Cuzco. Si el tiempo de vuelo entre esas dos ciudades se define según la siguiente función de densidad de probabilidad
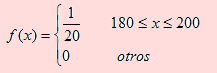
a) Qué porcentaje de vuelos tardará entre 84 y 96 minutos?
b) Si sólo el 5% de vuelos llega retrasado, cuál es el tiempo máximo para que un vuelo no llegue retrasado?
Solución
Sea X la variable aleatoria definida como “El tiempo que tarda el vuelo entre Lima y el Cuzco”.
a) Según los datos,

b) Decir que un vuelo llega retrasado significa que el tiempo que tarda el vuelo debe ser mayor que un tiempo “límite”, digamos t0. Según el problema tenemos P(X> t0 )=0.05 Como lo que queremos saber es cuál es ese límite y no sobrepasarlo, debemos hallar t0 tal que P(X &e; t0) = 0.05.
En efecto, P(X ≤ t0 )=0.05 implica que
P(X ≤ t0 )
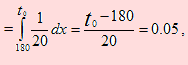
de donde
t0 = 180 + 0.05(20) = 181
Luego el tiempo máximo que debe tardar el vuelo para no llegar retrasado es 181 minutos.
Ejemplo 38
La duración (en horas ) de cierto producto perecible es una variable aleatoria continua X, cuya función de densidad de probabilidad viene dada por

a) Si un producto determinado todavía es aceptable después de 200 horas, cuál es la probabilidad de que dicho producto dure a lo más, 300 horas?
b) Se adquieren tres de tales productos. Cuál es la probabilidad de que ninguno tenga que ser reemplazado en las primeras 200 horas de uso? Cuál es la probabilidad de que los tres productos tengan que ser reemplazados durante las primeras 200 horas?. Cuál es la probabilidad de que, exactamente uno tenga que ser sustituida en las primeras 200 horas de uso?.
Solución
a) Sea X la variable aleatoria definida como la duración (en horas) de cierto producto.
Debemos encontrar la probabilidad condicional de que el producto dure a lo más 300 horas, sabiendo que estuvo funcionando (mayor de) después de 200 horas.
En efecto
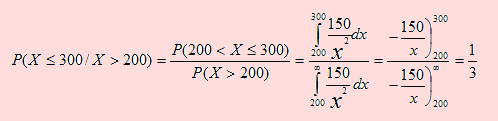
b) i) Definamos el evento M: “Ningún producto tenga que ser reemplazado en las primeras 200 horas de uso”.
Según esto, debemos encontrar primero la probabilidad de que uno de ellos no tenga que ser reemplazado antes de las 200 horas. Esto es debemos hallar P( X > 200 ).
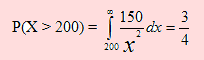
Ahora, encontrar P(M) significa evaluar P(M) = P(X>200)3. Luego P(M) = 27/64
ii)Sea N el evento “Los tres transistores deben ser reemplazados en las primeras 200 horas”.
Esto es P(N) = P(X ≤ 200)3 = (1 – P(X > 200) )3 = (1 – 3/4 )3 = 1/64
Definamos ahora el evento R : “Exactamente uno de los tres productos deben ser reemplazados en las primeras 200 horas de uso”.
Según esto, sólo uno de los tres productos debe ser reemplazado. Esto implica el uso de combinaciones para hallar el número de maneras de elegir uno de un total de tres. Esto multiplicar por la probabilidad de que uno de ellos se reemplaza antes de las 200 horas y los otros dos, después de las 200 horas.
Luego P(R) = C(3, 1)P(X ≤ 200) P(X > 200)2 = 3(1/4)(3/4)2 = 27/64.
Siguiente sesión.


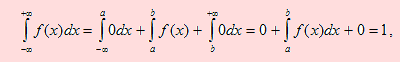 ,
,