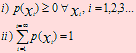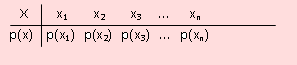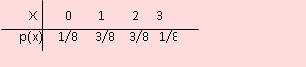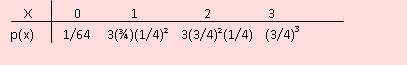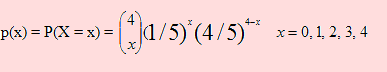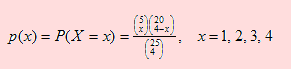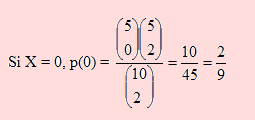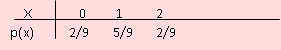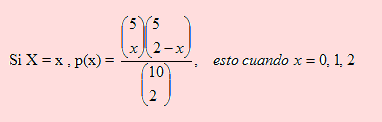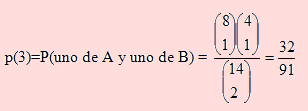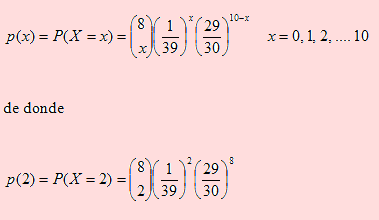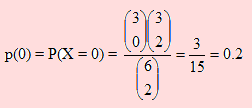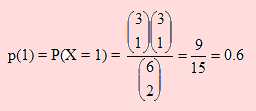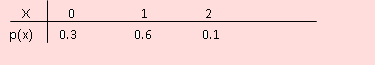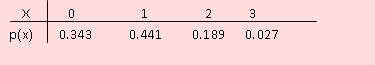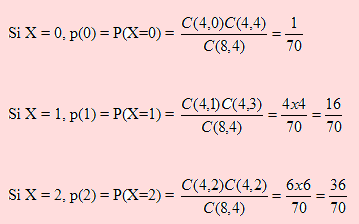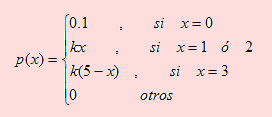Variables aleatorias

4.2. VARIABLES ALEATORIAS DISCRETAS

Sea X una variable aleatoria. Diremos que X es una variable aleatoria discreta si su espacio es un conjunto finito o numerablemente infinito.

Nota:

Decir que es finito significa que los valores que tome pueden ser cualquier número real; por lo general, toma valores enteros. Y decir que es numerablemente infinito, significa que siendo infinito, es posible enumerar cada uno de sus elementos; es decir, se puede saber quién es el anterior o el siguiente.

Ejemplo 10

Si se define a X como el número de accidentes ocurridos en la panamericana sur durante el año 2012, entonces X puede ser 0, 1, 2, 3, ...

Ejemplo 11

Se elige a 20 alumnos de una sección de Estadística Aplicada de la U. de Lima y se les pregunta por sus edades en días. En este caso definiremos a X como el número de días de un alumno. Según esto, X puede tomar valores entre 5840 días y 9125 días, considerando que se puede tener alumnos entre los 16 a 25 años.

Seguramente si X se define como la talla de estos alumnos, estaremos convencidos que X no constituye una variable aleatoria discreta.

Función de probabilidad

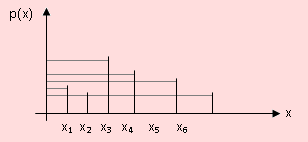
Sea X una variable aleatoria discreta, con R_X su espaciorango. Los posibles valores que toma X serán x₁, x₂, ... x_n, x_n+1,... Si a cada resultado posible x_i le asociamos un número real p(x_i) tal que p(x_i) = P(X = x_i), diremos que p(x_i) es la función de probabilidad de X, siempre que cumpla las siguientes condiciones:

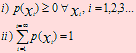
Podemos mostrar la función de probabilidad de X en una tabla como se indica en la siguiente figura:

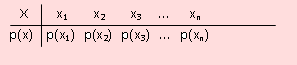
Gráfica de la función de probabilidad

Sea X una variable aleatoria discreta, con (x_i, p(x_i)) su distribución de probabilidad. La gráfica de la función de probabilidad se muestra en la siguiente figura.

Ejemplo 12

Se lanza al aire una moneda tres veces. Supongamos que se define a X como el número de caras obtenidas. Encuentre la función de probabilidad de X.

Solución
Por lo ya que sabemos de este ejemplo, X = 0, 1, 2, 3. Encontremos p(x_i).
Si x = 0 entonces p(0) = P(X = 0) = P({SSS}) = 1/8
Si x = 1 entonces p(1) = P(X = 1) = P({SSC, SCS, CSS}) = 3/8
Si x = 2 entonces p(2) = P(X = 2) = P({SCC, CSC, CCS}) = 3/8
Si x = 3 entonces p(3) = P(X = 3) = P({CCC}) = 1/8

En consecuencia, la distribución de probabilidad se muestra en la siguiente tabla.

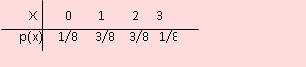
Ejemplo 13

Se sabe que al lanzar al aire una moneda, se obtiene cara tres veces más frecuentemente que sello. Si se lanza una moneda tres veces y se define a X como el número de caras obtenidas. Encuentre la distribución de probabilidad de X.

Solución
Si se define a X como el “Número de caras obtenidas”, entonces X = 0, 1, 2, 3.
Como sale cara tres veces más que sello, entonces la probabilidad de que salga cara en cualquier lanzamiento será 3/4, con lo cual p = 3/4 y q = 1 – p = 1/4 .
Si queremos obtener x caras, p(x) = P(X = x) es la probabilidad de obtener “x caras” y “3-x” sellos. La probabilidad de obtener x caras es (3/4)^x y “3-x” sellos es (1/4)^(3-x).
En los tres lanzamientos debemos obtener x caras. Esto lo hacemos de C(3, x) maneras. Luego la distribución de probabilidad de X será p(x) = P(X=x) = C(3, x) (3/4)^x (1/4)^(3-x) ; x = 0, 1, 2, 3.
La función de probabilidad mostrada en forma tabular es la siguiente:

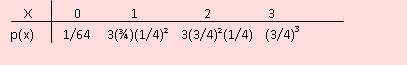
Ejemplo 14 De un lote que contiene 25, cinco de los cuales son defectuosos, se seleccionan en forma aleatoria a 4 de ellos. Sea X el número de defectuosos hallados.
Obtener la distribución de probabilidad de X si
a) los artículos son extraídos con reposición
b) los artículos son extraídos sin reposición

Solución

Caso a) La probabilidad de que el primero extraído sea defectuoso es 5/25.
Si cada uno de los productos extraídos se repone, entonces la probabilidad de que el siguiente extraído sea defectuoso sigue siendo la misma ya que los defectuosos siguen siendo 5 de un total de 25. En este caso el experimento genera una distribución de probabilidad conocida coma la binomial que la estudiaremos más adelante. Por ello si p(x) = P(X = x) es la función de probabilidad de obtener x artículos defectuosos y 4-x no defectuosos, entonces

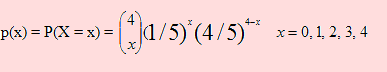
Caso b) En este caso los artículos se extraen sin reposición y esto implica que, si la probabilidad de extraer un defectuoso en la primera es 5/25, la probabilidad de que el segundo también sea defectuoso es 4/24 (ya que si salió defectuoso la primera vez ahora sólo quedan 4 defectuosos de un total de 24).
Usaremos la definición de probabilidad clásica para encontrar la función de distribución de probabilidad de X; es decir,

Debemos obtener X defectuosos:
El número de maneras de obtener x defectuosos de un total de 5 es lo mismo que formar grupos de x cada uno, de un conjunto de 5 elementos; esto es lo que se conoce como “combinaciones de 5 tomados de x en x”; es decir, C(5, x)
El número de maneras de obtener 4-x defectuosos de un total de 20, es formar grupos de 4-x tomados de un total de 20 que constituye “combinaciones de 20 tomados de 4-x en 4-x”; es decir C(20, 4-x).
El número de maneras de obtener x defectuosos y 4-x no defectuosos es C(5,x)C(20,4-x) por el principio de multiplicación. Esto nos da el número de casos favorables.

Veamos ahora los casos posibles:
Aquí se trata de formar grupos de 4 de un total de 25 en donde no interesa el orden. El número de maneras de hacerlo es C(25, 4), lo que constituye el espacio muestral.

Luego la probabilidad de la ocurrencia del evento X = x es

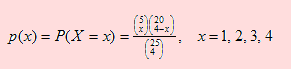
Ejemplo 15

Una dulcería tiene en su vitrina cinco huahuas de chocolate y cinco de guanábana, al mismo precio. Toda vez que el cliente no especifica su pedido y solicita dos, el encargado selecciona aleatoriamente dos de ellas. Si un cliente compra dos y no especifica el tipo de huahua, cuál es la función de probabilidad del número de huahuas de chocolate entregadas?

Solución
Sea X la variable aleatoria definida como “El número de huahuas de chocolate seleccionadas y entregadas al cliente”. Como se extrae sólo dos huahuas, los valores posibles de X son 0, 1 y 2.
Debemos observar también que el modelo de ensayo que representa seleccionar las dos huahuas implica que el ensayo es sin reposición, como es lógico.
Usando la definición de probabilidad clásica para encontrar la función de distribución de probabilidad de X; es decir,

Elegir 0 huahuas de chocolate ( X = 0 ) significa que las dos elegidas son de guanábana. Es decir, debemos encontrar el número de maneras de elegir 0 huahuas de chocolate y 2 de guanábana. De cuántas maneras elegir 0 huahuas de chocolate de un total de 5 y de cuántas maneras elegir 2 huahuas de guanábana de un total de 5 significa C(5,0)xC(5,2), lo que constituye el número de casos favorables. En cuanto a los casos posibles es C(10, 2). Luego

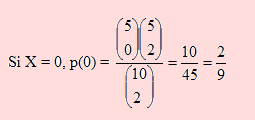
Usando el igual razonamiento, encontramos las probabilidades para los otros valores de X.
Luego la distribución de probabilidades de X viene dada por

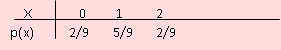
Observación:

Si se selecciona “x” tortas de chocolate, cuál será el valor de p(x)?.
Siguiendo el mismo razonamiento hecho para X=0, concluiremos que

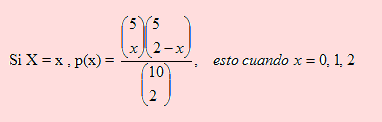
Este será el modelo de función de probabilidad hipergeométrico cuando el ensayo es sin reposición, en el cual la probabilidad de un resultado individual, favorable cambia cada vez que se hace un nuevo ensayo; a diferencia de los modelos binomiales que son generados por ensayos con reposición, donde la probabilidad de una ocurrencia favorable es constante. Este modelo de distribución lo estudiaremos también más adelante.

Ejemplo 16

Supongamos que los productos fabricados por tres máquinas A, B y C, se juntan al final del día. Supongamos que 8 productos provienen de la máquina A, 4 de la máquina B y 2 provienen de la máquina C. Un empleado que se encarga de transportar del almacén a los camiones recibe por cada producto proveniente de la máquina A, dos soles; por cada producto proveniente de B, recibe un sol; y por cada producto de C, recibe 0 soles. Si el empleado debe transportar dos productos, encuentre la función de probabilidad de la ganancia obtenida por el empleado.

Solución

Sea X la variable aleatoria definida como la “cantidad de soles recibido por el empleado al transportar dos productos cualquiera”.

Si los dos productos que transporta son de C, X = 0
Si los dos productos que transporta son de A, X = 4
Si los dos productos que transporta son de B, X = 2
Si transporta uno de A y uno de B, X = 3
Si transporta uno de A y uno de C, X = 2
Si transporta uno de B y uno de C, X = 1
Luego los posibles valores de X son X: 0, 1, 2, 3, 4

Como en el ejemplo anterior, usaremos la probabilidad clásica y tomaremos en cuenta que el transporte de los productos constituye un ensayo sin reposición.

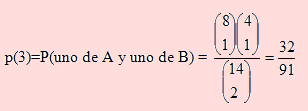
Luego, la función de distribución de X será

Ejemplo 17

Una agencia bancaria tiene tres cajeros automáticos. La probabilidad de que uno cualquiera de ellos falle después de un tiempo determinado de uso, es 0.1. Los cajeros operan independientemente uno de otro. En una hora determinada, cuál será la distribución de probabilidad del número de cajeros que fallen?

Solución

De acuerdo al problema, el funcionamiento de cada cajero es independiente uno de otro. La probabilidad de que uno de ellos falle es igual a 0.1. Sea X la variable aleatoria definida como “el número de cajeros que fallan en una hora determinada”. Según esto, pueden fallar 0, 1, 2 o los 3 cajeros; por lo que los valores posibles de X son 0, 1, 2, 3.

Sea F el evento “Un cajero falla” tal que P(F) = 0.1 y P(F’) = 0.9.

Con lo cual

p(0) = P(X=0) = P(F’F’F’) = 0.93 =0.729. Esto porque los eventos son independientes.
p(1) = P(X=1) = P(FF’F’ ó F’FF’ ó F’F’F)=C(3,1)P(FF’F’)=3(0.1)(0.9) 2 = 0.243
p(2) = P(X=2) = C(3,2)P(FFF’) = 3(0.1) 2 (0.9) = 0.027
p(3) = P(X=3) = C(3,3)P(FFF) = (0.1) 3 = 0.001

Luego la distribución de probabilidad del número de cajeros que fallen será

Ejemplo 18

Supongamos que la máquina 1 produce diariamente dos veces más items que la máquina 2. Sin embargo, el 4% de los items producidos por la máquina 1 tienden a ser defectuosos, mientras que sólo el 2% de los items producidos por la máquina 2 son defectuosos. Supongamos que la producción diaria de las dos máquinas se combina al final del día. Si se toma una muestra aleatoria de 10 items de este lote, cuál es la probabilidad de que la muestra contenga dos defectuosos?.

Solución

De acuerdo a los datos, de tres items que se produzca, dos provienen de la máquina 1; esto significa que si se extrae un item del lote, la probabilidad de que provenga de la máquina 1 es 2/3 y que provenga de la máquina 2 es 1/3. El diagrama siguiente refleja el resto de los datos.

P(M1) = 2/3; P(M2) = 1/3; P(D/M1) = 0.04 P(D/M2) = 0.02
Si D es el evento: el item elegido es defectuoso, entonces
P(D) = (2/3)(0.04) + (1/3)(0.02) = 1/30

Sea X la variable definida como el número de items defectuosos hallados en la muestra de 10.
Sea p = P(D) = 1/30 la probabilidad de éxito; es decir, de que un item de la muestra sea defectuoso.

Sea A el evento definido como “La muestra contenga dos defectuosos”

Según los datos, P(A) = p(2) = P(X = 2). Como la probabilidad de que un producto sea defectuoso es p = P(D) = 1/30, entonces, ocurre éxito cuando se extrae un artículo defectuoso, en este con p = 1/30. Ahora bien, el número de maneras de seleccionar x = 2 defectuosos en una muestra de tamaño 10 es C(10, 2). La probabilidad de que en un grupo cualquiera de estas C(10, 2) maneras haya 2 defectuosos es (1/30)(1/30)=(1/30)^2 “y” los otros 10-2 sean no defectuosos es (29/30)^8. Por ello, la función de probabilidad para x defectuosos será

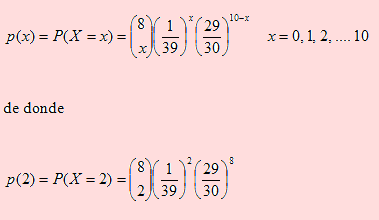
Ejemplo 19

Se tiene una urna con tres fichas negras y dos rojas. Si se extrae sucesivamente y sin reposición de una en una hasta obtener una negra y se define a X como el número de extracciones que se debe realizar hasta que salga una ficha negra, determine la función de probabilidad de X.

Solución

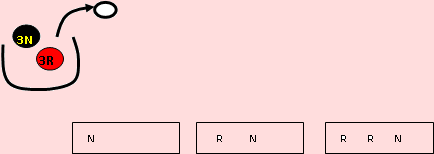
Ante todo, el espacio muestral Ω , está formado por Ω = {N, RN, RRN }.
Sea X: El número de extracciones que debe realizarse hasta obtener una ficha negra

Como en la urna hay dos rojas, los tres rectángulos muestran las tres situaciones que pueden presentarse, no importa el orden. En el primer caso X toma el valor 1, ya que se ha realizado una extracción. En el segundo se han realizado dos y en el tercero X tomará el valor 3. Luego los posibles valores de X son 1, 2 y 3.

Si X = 1 entonces p(1) = 3/6 = 0.6
Si X = 2 entonces p(2) = (2/5(3/4) = 0.3
Si X = 3 entonces p(3) = (2/5)(3/4)(3/3) = 0.1

Luego la función de probabilidad de X viene dada por

Ejemplo 20

Se lanza un dado hasta que salga un 3 ó 5. Si se define a X como el número de veces que debe lanzarse el dado hasta obtener éxito, obtenga la función de probabilidad de X.

Solución

Este ejemplo es una generalización del tipo de ensayo del ejemplo anterior. Cada vez que se lanza el dado, puede ocurrir dos únicos posibles resultados: éxito (sale un 3 ó un 5) o fracaso (sale otras caras). En el momento en que ocurre éxito por primera vez, termina el ensayo. Si p = P(E) es la probabilidad de que ocurra éxito, entonces p = 1/3 y si q = P(F) es la probabilidad de fracaso, q = 1 – p = 2/3. El siguiente esquema orientará nuestro análisis.

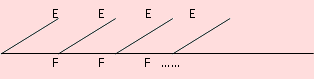
Algunos de los elementos del espacio muestral son los siguientes:
Ω = { E, FE, FFE, FFFE, FFFFE, ...}
de igual manera, los posibles valores que pueda tomar X son: 1, 2, 3, ...
X = 1 significa que se obtuvo éxito en el primer ensayo. Como p(1) = P(X = 1) = P(E) tenemos p(1) = P(X=1) = 1/3.

X = 2 significa que se obtuvo éxito en el segundo ensayo, lo que significa que el primero tuvo que ser fracaso. Luego p(2) = P(X = 2) = P(FE) = (2/3)(1/3).

Ocurre lo mismo con X = 3. Es decir p(3) = P(X = 3) = P(FFE) = (2/3)(2/3)(1/3). Del mismo modo, X = 4 significa que p(4) = (2/3)3(1/3).

Supongamos que “X = x “ es el evento “el primer éxito” ocurre en el “x-ésimo” ensayo. Diremos entonces que en los “x-1” ésimos ensayos hubo fracaso y éxito en el último. Por ello, la función de probabilidad de X será

Ejemplo 21

Un grupo de investigadores de mercado está formado por tres hombres y tres mujeres. Si el responsable del grupo desea elegir aleatoriamente a dos de ellos para una labor especial y definimos a X como el número de mujeres seleccionadas, obtenga la función de probabilidad de X.

Solución

Como en el grupo hay tres mujeres y tres hombres y se extrae a dos de ellos, X tomará valores 0, 1, 2. Hallemos la probabilidad para cada valor de X
X = 0 significa que debe elegirse a dos hombres. El problema consiste ahora en elegir a dos hombres de un grupo de 3. Esto constituye una combinación de 3 elementos tomados de 2 en dos. Podríamos decir lo mismo de las mujeres: El número de maneras de elegir cero mujeres de un total de 3, representa combinaciones de 3 tomados de 0 en 0. Y como deben ocurrir los eventos “cero mujeres” y “dos hombres” entonces, la probabilidad de que ocurran será el producto de ambos, por el principio de multiplicación. El espacio muestral estará constituido por el número de combinaciones de 6 elementos tomados de 2 en dos. Por ello la probabilidad de elegir “cero” mujeres es

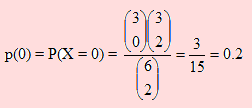
Analicemos el caso X = 1. Se trata de elegir una mujer dentro de un total de 3, y un hombre dentro de un total de 3 hombres. La probabilidad de que esto ocurra es

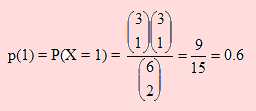
Dejamos para el lector el caso X = 2.
La función de probabilidad viene dada por:

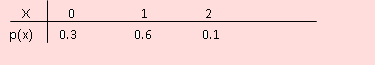
Ejemplo 22

La probabilidad de que un agente vendedor realice una entrevista efectiva (realice una venta) es igual a 30%. Cierto día entrevista a 3 clientes potenciales. Si se define a X como el número de clientes que firman un contrato de venta, encuentre la distribución de probabilidad de X.

Solución

Sea X la variable aleatoria que representa “el número de clientes que firman un contrato de venta”. Según esto, los posibles valores de X son 0, 1, 2 y 3. Como la probabilidad de que la entrevista sea efectiva(firmen un contrato de venta) es igual a 0.30, definamos
Sea F el evento: “Firma un contrato de venta”, y N el evento “No firma el contrato”. X = 0 significa que ninguno de los tres clientes firma, es decir ocurre el evento compuesto NNN. Luego p(0) = P(X = 0) = P(NNN) = 0.73 . Esto se puede expresar en función de los que firman el contrato: P(X = 0) = P(NNN) = (0.3)0 (0.7)3 .
“X = 1” puede ser expresado como FNN ó NFN ó NNF. Como P(FNN) = PNFN) = P(NNF). El número de ocurrencias de una F dentro de un grupo de tres se representa mediante las combinaciones de 3 elementos tomados de uno en uno; es decir, C(3,1) = 3. Luego

p(1) = P(X = 1) = C(3,1)(0.3)¹(0.7)²

Del mismo modo, “X=2” tiene por probabilidad p(2) = P(X=2) = C(3,2)(0.3)²(0.7)¹

Por ello, la función de distribución de X viene dada por

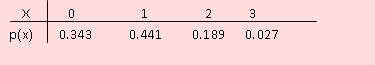
Ejemplo 23

La empresa “Refrigerando” tiene dos talleres para la fabricación de refrigeradoras. Al final de un día de producción se tiene 4 unidades del taller A y 4 del taller B. Puesto que uno de los talleres ha estado funcionando mal, se sospecha que la mitad de la producción de ese día sea defectuosa. Obtenga la distribución de probabilidad del número de refrigeradoras defectuosas provenientes del taller A, si se selecciona 4 del grupo y se somete a prueba. Construya su gráfica.

Solución

Sea X la variable aleatoria definida como “El número de refrigeradoras del taller A que son defectuosas”. Al seleccionar una refrigeradora y probarla, esta puede ser defectuosa con probabilidad 0.5 y no defectuosa con probabilidad 0.5. Como se extraen 4 del grupo producido en un día, los valores de X son 0, 1, 2, 3 y 4. Como la forma de selección de las refrigeradoras constituye un ensayo sin reposición, usaremos combinaciones para encontrar el número de casos favorables y posibles para usar la probabilidad clásica y responder a la pregunta.

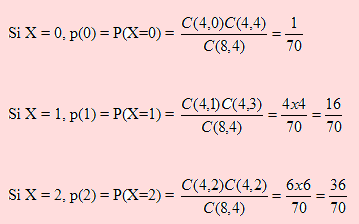
Dejamos para el lector completar para X = 3 y X = 4, con lo cual la distribución de probabilidad del número de defectuosos provenientes del taller A será

Ejemplo 24

La firma “Pregunta S.A.” realiza su acostumbrado trabajo de campo durante una campaña electoral. Para lograr una entrevista debe realizar varios intentos independientes, por la dificultad de conseguir personas que acepten la entrevista. Si la probabilidad de lograr una entrevista exitosa es 0.70, determine la distribución de probabilidad del número de intentos realizados hasta conseguir una entrevista exitosa.

Solución

Sea X la variable aleatoria definida como el “Número de intentos realizados hasta obtener una entrevista exitosa”. Sea p = 0.7 la probabilidad de una entrevista exitosa.

Por cada entrevista exitosa se tiene p = 0.7 y por cada entrevista fallida q = 1-p = 0.3. El siguiente esquema podría graficar la secuencia de nuestros intentos, en donde todos son fallidos hasta el último y sólo éste, que es exitoso.

Supongamos que se han realizado “x” intentos hasta que se produjo el primer éxito. Esto significa que los “x-1” – ésimos intentos han sido fracasos y sólo el “x”-ésimo ha sido éxito. Como cada fracaso ocurre con probabilidad q = 0.3, siendo independientes los intentos, los “x-1” intentos ocurren con probabilidad q(x-1) y en conjunto: los fallidos con el exitoso ocurren con probabilidad (q(x-1) )(0.7). Luego la función de probabilidad de X será

p(x) = P(X = x) = (0.3)^(x-1)(0.7) para x = 1, 2, 3, ....

Ejemplo 25

Sea X la variable aleatoria definida como el número de cuentas que tiene un cliente en SUPER BANK. Suponga que la función de probabilidad de X está definida por

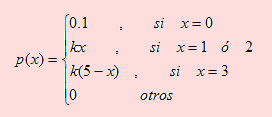
a) Qué porcentaje de clientes tiene?
a.1) exactamente dos cuentas?
a.2) a lo más dos cuentas?

b) El Gerente financiero de SUPER BANK afirma que “con las nuevas políticas adoptadas por SUPER BANK se ha logrado que más del 85% de nuestros clientes tengan al menos dos cuentas”. ¿Se puede decir que el Gerente tiene razón?

Solución

De los datos del problema podemos inferir que X es una variable aleatoria discreta. Ante todo encontremos el valor de k de forma que p(x) sea la f. de probabilidad de X.

Si ∑p(x) = 1 , entonces k+2k +k(5-3) = 1. Despejando k obtenemos k = 0.2

a)
a.1) Debemos encontrar p(2) = P(X = 2) = 0.2(5-3) = 0.4. Es decir, el 40% de clientes tienen exactamente dos cuentas.

a.2) Qué porcentaje de clientes tienen, a lo más dos cuentas, significa obtener la probabilidad de que X = 0, ó X = 1, ó X = 2. Es decir, debemos hallar P(X = 0 ó X = 1 ó X = 2) = p(0) + p(1) + p(2) = 0.0 + 0.2 + 0.40= 0.60. En otras palabras, el 60% de los clientes tiene a lo más dos cuentas.

b) Para saber si el Gerente tiene razón o no, debemos encontrar la probabilidad de que X sea mayor o igual a 2.
En efecto P(X ≥ 2) = p(2)+p(3) = 0.2(2) + 0.2(5-3) = 0.8.
Según esto, el 80% de los clientes tiene al menos dos cuentas en el banco, lo que contradice al Gerente, por lo que diremos que él no tiene razón.

Siguiente sesión.