CAPÍTULO 4

VARIABLES ALEATORIAS Y DISTRIBUCIONES DE PROBABILIDAD

4.1 Variable aleatoria
4.2 Variable aleatoria discreta. Función de probabilidad
4.3 Variable aleatoria continua. Función de densidad de probabilidad
4.4 Función de distribución acumulada
4.5 Problemas propuestos
4.6 Valor esperado de una variable
4.7 Varianza de una variable
4.8 Problemas propuestos
4.9 Distribuciones continuas: Caso de variable aleatoria discreta
4.10 Problemas propuestos
4.11 Distribuciones conocidas: Caso de variable aleatoria continua
4.12 Problemas propuestos
4.13 Otras distribuciones continuas conocidas
4.14 Variables aleatorias bidimensionales
4.15 Problemas propuestos

4.1. VARIABLE ALEATORIA


Definición de variable aleatoria

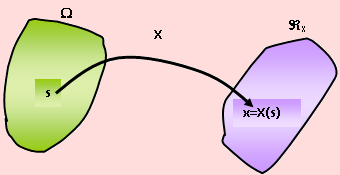
Sea ζ un fenómeno aleatorio y Ω el espacio muestral asociado a dicho experimento. Diremos que la función X es una variable aleatoria si para cada elemento s del espacio muestral, le hace corresponder un número real x tal que x = X(s).

Es decir, X es una variable aleatoria si ∀ s ε Ω , ∃ un x ε R_X / x = X(s)

Esto se aprecia en la siguiente figura.





Ejemplo 01 ζ ₁: Supongamos que se lanza al aire una moneda tres veces. Si ζ es el fenómeno aleatorio, su espacio muestral será Ω = {SSS, SSC, SCS, CSS, SCC, CSC, CCS, CCC}. Si definimos a X como la variable aleatoria que representa "el número de veces que ocurra cara", entonces X(SSS) = 0; ; es decir, el número de caras obtenidas puede ser cero, y esto ocurre cuando se obtiene tres sellos; del mismo modo, se obtendrá una cara siempre que X(SSC) = X(SCS) = X(CSS) = 1; o dos caras cuando X(SCC) = X(CSC) = X(CCS) = 2 y también, X(CCC) = 3. De todo ello deducimos que, si se lanza una moneda tres veces y se define a X como el número de caras obtenidas, los posibles valores que tome X serán 0, 1, 2, 3. Luego el espacio rango de X será R_X = { 0, 1, 2, 3 }.

Ejemplo 02 ζ ₁: De un lote de productos, en donde el 10% son defectuosos, se elijen al azar a 5 de ellos. Si se define a X como el número de productos defectuosos seleccionados, entonces X tomará los valores: 0, 1, 2, 3, 4, 5. Esto significa que el espacio rango de X será R_X = {0, 1, 2, 3, 4, 5}.

Ejemplo 03 ζ ₁: De 5 varones y 4 damas, se elige un comité de tres miembros. Se define a X como el número de damas que pueden conformar el comité
En este caso X: 0, 1, 2, 3. Según esto, el espacio rango R_X = {0, 1, 2, 3}.

Ejemplo 04 ζ ₁: Una nave de combate lanza proyectiles a una vía férrea. Ésta quedará destruida si si el proyectil cae a 30 metros de la vía. Se define a X como la distancia entre el punto de impacto del proyectil y la vía férrea.

La variable aleatoria X en este caso, toma infinitos valores dentro de un rango; es decir, R_X = { x ε R / -c ≤ x ≤ c }, donde "c" es la máxima distancia entre el punto de impacto del proyectil y la vía férrea.

Eventos equivalentes


Sea ζ un experimento aleatorio. Sea Ω el espacio muestral asociado a ζ. Sea X una variable aleatoria definida sobre Ω con R_X su espacio rango.
Si B es un evento de R_X; es decir, B está contenido en R_X y A se define como A = { s ε Ω / X(s) ε B } entonces diremos que A y B son dos eventos equivalentes.
. En otras palabras, un evento B, del espacio rango es equivalente a otro evento A, del espacio muestral, si cada elemento del evento A del espacio muestral tiene como imagen otro evento B del espacio rango, según la definición de X.

Ejemplo 05

En el primer ejemplo visto en esta sección, vimos que si se define a la variable aleatoria X como el número de caras obtenidas, el evento B: “Obtener 0 caras” será equivalente con el evento A: “Obtener 0 caras”. En efecto, A = { SSS } y según la definición, B = {x / x = X(SSS) = 0 }. Si ocurre A entonces, y sólo entonces, ocurre B.
 

Ejemplo 06 Tomando el mismo ejemplo supongamos ahora que se define el evento B como “Salen por lo menos dos caras”. En este caso B = {x εR_X/ x = 0, 1, 2 }; B = { 0, 1, 2 }. En el espacio muestral Ω debe ocurrir el evento A: “Obtener a lo más dos caras”, lo que por extensión se define como A = {SSS, SSC, SCS, CSS, SCC, CSC, CCS }.
En este caso
0 = X(SSS),
1 = X(SSC) = X(SCS) = X(CSS)
2 = X(SCC) = X(CSC) = X(CCS)

Probabilidad en eventos equivalentes

Sea X una variable aleatoria y B un evento de R_X. Sea A un evento de Ω equivalente con B. Si P(A) es la probabilidad de la ocurrencia de A y P(B) es la probabilidad de la ocurrencia de B, entonces P(A) = P(B) siempre que A y B sean eventos equivalentes, es decir siempre que A = {s ε Ω / X(s) ε B}.

Ejemplo 07

Tomando en cuenta el ejemplo anterior, sea B = {X / X = 0 }. El evento equivalente a B deberá ser A = {SSS}.
En consecuencia, P(B) = p(0) = P(X = 0) = P(X(SSS)) = P(A) = 1/8

Nota:

Evaluar probabilidades en el espacio rango de X es evaluar probabilidades en A.

Ejemplo 08

Si se lanza al aire una moneda tres veces, ¿cuál es la probabilidad de obtener a lo más, dos caras?

El espacio muestral para este ensayo ya lo hemos visto. Según la pregunta, X se debe definir “como el número de caras obtenidas”, entonces definimos a B como “Obtener a lo más dos caras”.
Según esto, B = {0, 1, 2 } = {x / x ≤ 2 }. Y el evento equivalente a B será
A = {SSS, SSC, SCS, CSS, SCC, CSC, CCS }
Como se sabe, P(A) = 7/8. Si B y A son eventos equivalentes, entonces P(B) = 7/8.

Tipos de variable aleatoria

Una variable aleatoria es discreta si su espacio rango es finito (toma valores enteros) o numerablemente infinito (se puede identificar a cada uno de ellos y se puede ordenar) mientras que una variable aleatoria es continua si su espacio rango es infinito. Nota:

Si bien en el caso de una variable discreta el espacio rango se puede expresar por comprensión o extensión, en el caso de una variable continua sólo se puede expresar por comprensión mediante el uso de cualquiera de las forma de intervalo.

Ejemplo 09: De identificación

Diga si las siguientes variables aleatorias que se mencionan son discretas o continuas:

a) El número de caras que se obtiene al lanzar al aire una moneda 1000 veces
b) El tiempo que un cliente tarda en la cola de una caja hasta ser atendido
c) El tiempo que el cajero tarda en atender el cliente
d) El tiempo en minutos que un conductor espera para pagar el peaje en una garita
e) El número de alumnos que repiten el curso de Estadística en cierto semestre
f) El número de veces que un alumno se matricula en una determinada asignatura
g) El valor estimado en dólares de una casa de dos plantas
h) El número de cuentas por pagar que una oficina bancaria tiene en cierto momento
i) El número de kilómetros que recorre un taxista diariamente
j) El número de demandas por día que recibe una compañía de seguros
k) El número de accidentes que se registra anualmente en la Vía Expresa
l) El tiempo entre un accidente y otro durante un año, en la Vía Expresa

Solución

Son variables aleatorias discretas:
     a)      e)     f)     j)     k)
Son Variables Aleatorias Continuas:
    b)     c)     d)     g)     h)     i)     l)

Siguiente sesión.