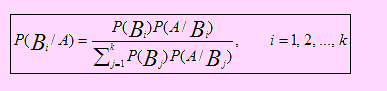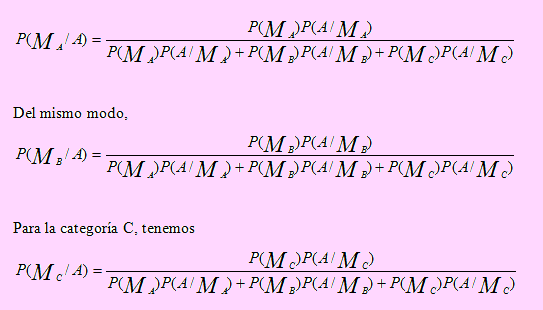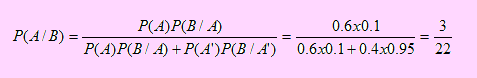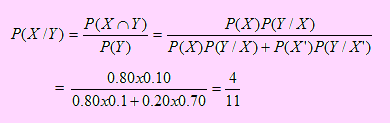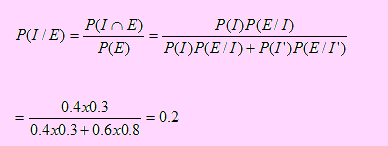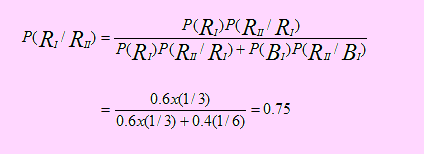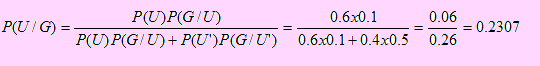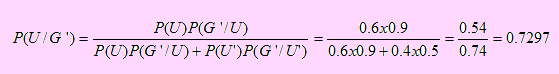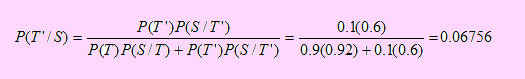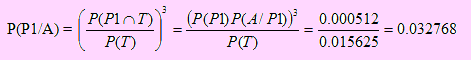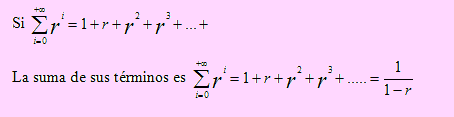3.5 PROBABILIDAD TOTAL

Partición de un espacio muestral

Sea Ω el espacio muestral asociado al experimento ζ. Sean B₁, B₂, B₃,..., B_k eventos de &Omega. Diremos que B₁, B₂, B₃,..., B_k constituye una partición del espacio muestral Ω, si se satisface las siguientes condiciones:

i) B_i ∩ B_j = φ     ∀ i,     ∀ j    , con i, j = 1, 2, … k.

ii) P(B_i ) ≠ 0, ∀ i = 1, 2, …, k

iii) B₁ ∪ B₂ ∪ B₃ ∪ ... ∪ B_k = Ω

En la figura adjunta, podemos apreciar que los eventos Bi no son vacíos; la unión de todos ellos genera el espacio muestral; y son eventos mutuamente excluyentes, dos a dos.



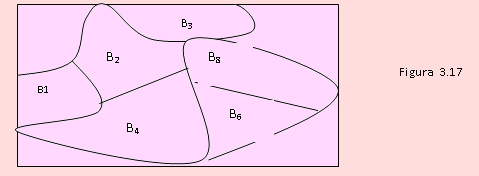
Luego la secuencia de eventos B₁, B₂, B₃,..., B_k constituye una partición de Ω.

Ejemplo 26

Sea Ω el espacio muestral asociado al experimento de lanzar dos dados por una sola vez. En este caso

Ω = {(1,1),(1,2),(1,3),(1,4),(1,5),(1,6),(2,1),(2,2),(2,3),(2,4),..., (6,4),(6,5),(6,6)}.
SeaB₁ : “La caras superiores son iguales”
B₂ : “La suma de las caras es igual a 5”
B₃ : “El producto de las caras es 12”
B₄ : “La suma de las caras es 11”
B₅: “El producto de las caras es 32”
B₆: “Los números de las caras mostradas es (4,5)

La colección de eventos B₁, B₂, B₃, B₄, B₅, B₆ constituye una partición de Ω. Dejamos para el lector la comprobación del mismo.


Teorema de la probabilidad total

Sea B₁, B₂, B₃,..., B_k , una partición de eventos del espacio muestral Ω. Sea A un evento cualquiera de Ω. Entonces

P(A ) = P(B₁ ) P(A / B₁)P(B₁ ) P(A / B₂) ... P(B_k-1 ) P(A / B_k)

donde P( A / B _j) > 0,       ∀ j = 1, 2, ..., k.



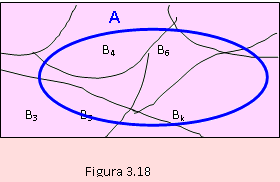
Según el diagrama de Venn de la Figura 3.18, el evento A es un evento compuesto que puede ser expresado como

A = A ∩ B₁ ∪ A ∩ B₂ ∪ ... ∪ A ∩ B_k

Tomando probabilidades a ambos lados de la igualdad tenemos

P(A) = P(A ∩ B₁ ∪ A ∩ B₂ ∪ ... ∪ A ∩ B_k)

= P(A ∩ B₁) + P(A ∩ B₂) + ... + P(A ∩ B_k)       (1)

Recordando que A ocurre sabiendo que B_j ya ha ocurrido, podemos usar la probabilidad condicional para encontrar la probabilidad de cada uno de los términos de la suma, ya que



Ejemplo 27

Una encuesta realizada en el centro de Huacho, encontró que el 70% de los vehículos que se desplazaban por sus principales arterias, presentaban fuerte emanación de monóxido de carbono. De todos estos vehículos, el 80% eran de transporte público. De aquellos que no despedían monóxido, sólo el 10% eran de transporte público. Si un día determinado, nos ubicamos en la esquina de las avenidas Echenique y 28 de Julio, y elegimos un vehículo cualquiera, ¿cuál es la probabilidad de que pertenezca al transporte público?

Solución

Sean los eventos:
G: “El vehículo seleccionado emite monóxido”<
T: “El vehículo seleccionado perteneceal transporte público”



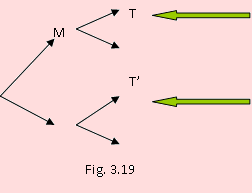
En el diagrama de árbol de la figura 3.19 podemos apreciar, según nos muestra las flechas, que el evento T ocurre dedos formas: Que sea de transportepúblico(T) y emita monóxido (T ∩ M) oque sea de transporte público y no emitamonóxido (T ∩ M’ ).

Por ello, T = T ∩ M ∪ T ∩ M’. Y como los eventos M y M’ forman una partición de Ω , podemos aplicar el Teorema de la Probabilidad Total. Por lo que P(T) = P(M)P(T/M) + P(M’ )P(T/M’ )
= 0.7 x 0.8 + 0.3 x 0.1
= 0.59

Ejemplo 28

Una máquina es sometida a evaluación. Por recientes resultados, se sabe que el 20% de los productos que elabora, son defectuosos. Si el control del rendimiento se le encarga a un técnico, la probabilidad de que diagnostique correctamente cuando el producto es defectuoso, es 0.85, mientras que se equivoque en su diagnóstico, es 0.35. Si se elige un producto controlado por dicho técnico, calcule la probabilidad de que

< a) sea un producto diagnosticado como defectuoso
b) sea un producto que pasó como bueno

Solución

Sean los eventos:
A: El producto es diagnosticado como defectuoso
D: El producto es defectuoso



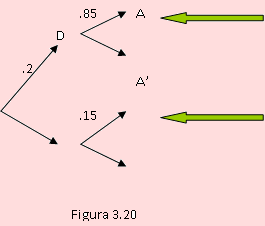
a) Según la figura 3.30, P(A) = P(D)P(A/D) + P(D’ )P(A/D’ )

          = 0.2 x 0.85 + 0.8 x 0.35
          = 0.45

b) Contrariamente al caso a), se trata de trabajar con los ramales no indicados por las flechas. Según la figura, P(A’ ) = P(D)P(A’ /D) + P(D’ )P(A’ /D’ )
          = 0.2 x 0.15 + 0.8 x 0.65
          = 0.55

Ejemplo 29

Una fábrica produce diariamente 10 recipientes de vidrio. Se puede suponer que hay una probabilidad constante de p = 0.1 de producir uno defectuoso. Antes de que estos depósitos se almacenen son inspeccionados y los defectuosos puestos a parte. Supongamos que hay una probabilidad constante r = 0.1 de que un recipiente defectuoso sea mal clasificado. Si todos los recipientes que se fabrican en un día se inspeccionan el mismo día, ¿cuál es la probabilidad de que al elegir un producto de aquellos que están clasificados, se encuentre que es un producto defectuoso? ¿Cuál es la probabilidad de que un producto defectuoso sea bien clasificado?

Solución

Este es un problema similar al anterior. Hagamos un razonamiento analítico, antes que gráfico:

Sea D: “El producto es defectuoso” y B: “El producto fue bien clasificado”. Si se elige un producto y éste es defectuoso, entonces puede ser un producto realmente defectuoso y estar bien clasificado; es decir ocurre el evento compuesto: D ∩ B. Del mismo modo, puede ser que siendo un producto no defectuoso, se clasificó mal, en cuyo caso está entre los defectuosos; es decir, D’ ∩ B’. Luego D ocurre cuando el evento D ∩ B ó D’ ∩ B’ ocurre. Como esta unión está formada por eventos mutuamente excluyentes,

P(D) = P(D ∩ B) + P(D’ ∩ B’). Pero B ocurre sólo cuando D ha ocurrido, igual que B’ y D’; es decir, usando el Teorema de la probabilidad Total, tenemos

P(D) = P(D)P(B/D) + P(D’)P(B’/D’) = 0.1 x 0.9 + 0.9 x 0.1 = 0.18

En cuanto a la segunda pregunta, diremos lo siguiente: Como sabemos que el producto es defectuoso y queremos que también esté mal clasificado, entonces, debemos encontrar la probabilidad del evento D  B. En efecto, P(D  B) = P(D)P(B/D) = 0.1 x 0.9 = 0.09.

Ejemplo 30

Una Compañía dedicada al transporte de petróleo crudo desde la selva cuzqueña desea construir un túnel trasandino para el transporte desde los pozos hasta el Callao. Para ello, el gobierno peruano debe dictar ciertas normas que traban la inversión y la forma de distribución final de las utilidades. Si el gobierno aprueba estas normas, la probabilidad de que la Cía. construya dicho túnel, es de 0.95, mientras que sólo se tiene la probabilidad 0.15 de construcción del túnel, si no se aprueban dichas normas.

Basándose en la información disponible, la compañía estima que hay una probabilidad de 0.80 de que el gobierno apruebe las normas. ¿Cuál es la probabilidad de que la compañía construya el túnel interandino?



Solución

Definamos los eventos:
A: “El gobierno aprueba las normas”
C: “La compañía construye el túnel interandino”<br>
<b>
<h3>3.5 PROBABILIDAD TOTAL</h3>
</b><br>

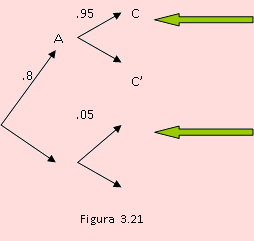
Según el problema, podemos construir nuestro diagrama de árbol, como se muestra en la figura 3.20.

Debemos hallar la probabilidad del evento C, que como sabemos, implica aplicar el teorema de la probabilidad total.
En este caso

P(C ) = P(A  C) + P(A’ C) = P(A) P(C/A) + P(A’)P(C/A’) = 0.8x0.95 + 0.2x0.15 = 0.79

Ejemplo 31

Los servicios de estudio de una empresa que proyecta introducir su producto en un mercado donde sólo tendría un competidor, estima que, al finalizar el ejercicio económico, sus ventas superarán las 200,000 unidades con una probabilidad de:

i) 0.1, si el precio fijado por la empresa competidora para su artículo es “bajo”;
ii) 0.5, si el precio fijado por la empresa competidora para su artículo es “medio”;
iii) “x”, si el precio fijado por la empresa competidora para su artículo es “alto”

Además por situaciones anteriores, el servicio de estudios determina que la probabilidad de que la empresa competidora:
Fije precio “bajo” es 0.2
Fije precio “medio” es 0.5
Fije precio “alto” es 0.3
También el estudio de la empresa determina que la probabilidad de que las ventas de la empresa superen las 200,000 unidades es 0.51. Determine el valor de “x”.

Solución

A continuación se muestra el diagrama de árbol para el problema



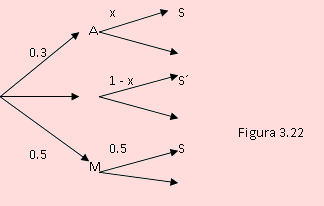
En este caso, definimos
A: “El precio es alto”
M: “El precio es medio”
B: “El precio es bajo”
S: “Supera las 200,000 u.”
Del mismo modo, el evento
S = S ∩ A ∪ S ∩ M ∪ S ∩ B
de donde

P(S) = P(A)P(S/A) + P(M)P(S/M) + P(B)P(S/B)
0.51 = 0.3 x X + 0.5 x 0.5 + 0.2 x 0.1
despejando X, encontramos X = 0.8

Ejemplo 32

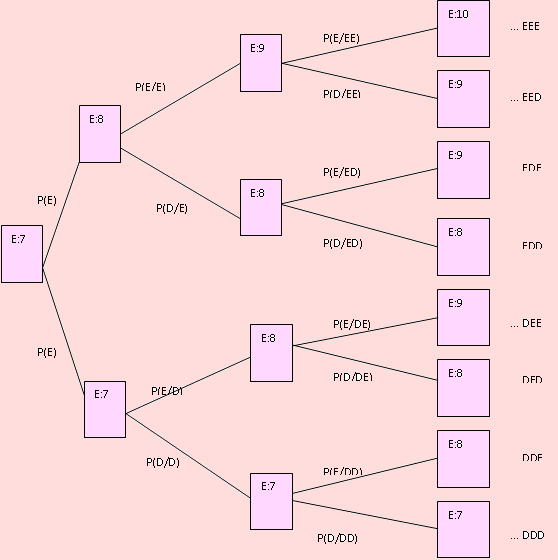
De una baraja de cartas se extrae una muestra de 3, de la siguiente manera: se empieza con un grupo de 12 cartas: 7 espadas y 5 diamantes. En cada ensayo se extrae una carta, se observa el tipo de carta y se devuelve, junto con otra carta adicional del mismo tipo. ¿Cuál es la probabilidad de que el número de espadas en el grupo de cartas, antes de la tercera extracción, sea 8, dado que la muestra contiene dos espadas y un diamante?

Solución

Sean los eventos:
A: “La muestra contiene dos espadas y un diamante”
B: “El número de espadas antes de la tercera extracción es 8”
E: “La carta es una espada”
D: “La carta es un diamante”
El evento A es un evento compuesto, tal que A = EED ∪ EDE ∪ DEE; con lo cual,

3.6 TEOREMA DE BAYES

Sean B₁, B₂, B₃,…, B_k, una partición de eventos del espacio muestral Ω. Sea A un evento cualquiera de Ω. Entonces



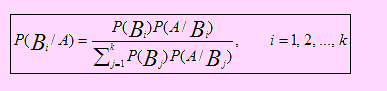
Ejemplo 33

Una compañía de seguros de taxis clasifica a los choferes en tres categorías: A, B y C. El 30% de los choferes que recurren para asegurarse, pertenecen a la categoría A; el 50% a la categoría B y sólo el 20% de la categoría C. La probabilidad de que un chofer de la categoría A tenga un accidente durante un año determinado, es 0.01. Para uno de la categoría B, es 0.03 y 0.10 para los de la categoría C. Si un día uno de los taxistas asegurados sufre un accidente, ¿cuál es la probabilidad de que pertenezca a la categoría A, B ó C?

Solución

Como primero se detecta (primer experimento) la categoría a la que pertenece el taxista, diremos que los eventos: “Categoría A, B o C”, ocurren primero. El segundo experimento consiste en la ocurrencia o no del accidente, lo que genera los nodos de la derecha del árbol.



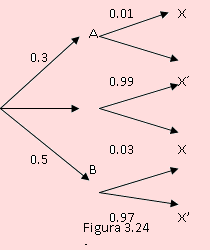
Sea M_A: “El chofer pertenece a la categoría A”
       M_B: “El chofer pertenece a la categoría B”
       M_C: “El chofer pertenece a la categoría C”
        X: “El taxista sufre un accidente”

Según esto, debemos encontrar

- La probabilidad de que el taxista pertenezcaa la categoría Mi, sabiendo que ha ocurrido X;es decir, P(Mi/X), i = A
- La probabilidad de que el taxista pertenezcaa la categoría Mi, sabiendo que ha ocurrido X;es decir, P(Mi/X), i = B
- La probabilidad de que el taxista pertenezcaa la categoría Ci, sabiendo que ha ocurrido X;es decir, P(Mi/X), i = C.

Aplicando el Teorema de Bayes, tenemos



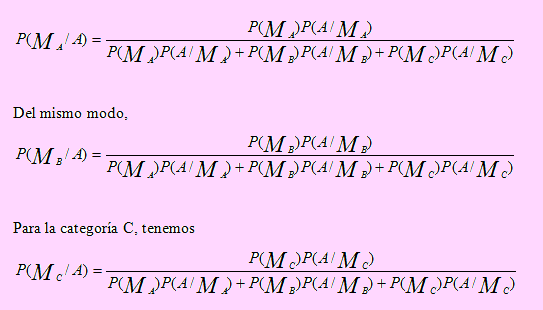
Dejamos para el lector reemplazar las probabilidades correspondientes tomando en cuenta los valores que se tienen en el diagrama de árbol.

Ejemplo 34

Todas las noches el señor García llega tarde a su casa. La señora García, que es una buena esposa, le deja encendida la luz de la entrada a la casa. La probabilidad de que el señor García llegue pasado de copas es 0.60. Si ha bebido, hay una probabilidad de 0.90 de que olvide apagar la luz, en tanto que ésta es sólo de 0.05, si llega sobrio.

a) ¿Cuál es la probabilidad de que el señor García apague la luz en una noche cualquiera?
b) Dado que el señor García apagó la luz, una cierta noche, ¿cuál es la probabilidad de que haya llegado pasado de copas?
Solución

Sean los eventos:
A: Llega pasado de copas
B: Apaga la luz



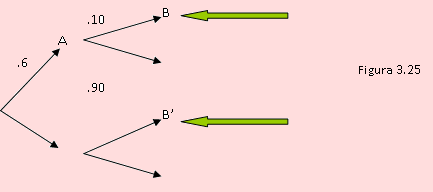
a) Debemos hallar la probabilidad de B.
Según el diagrama anterior, para encontrar la probabilidad de B, debemos usar el teorema de la probabilidad total. En efecto,
P(B) = P(A)P(B/A)+P(A’)P(B/A’)
        = (0.6)(0.10) + (0.4)(0.95)
        = 0.44

b) Sabiendo que el evento B ha ocurrido, se nos pide encontrar P(A/B).

Usando el Teorema de Bayes



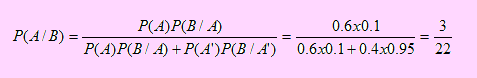
Ejemplo 35

El profesor Márquez dicta un curso de Estadística y quiere tomar una prueba en cada clase. Sabedor de que a veces se olvida de ir a preparar su clase, ha dado instrucciones a su Jefe de Prácticas que se haga cargo de la clase cuando él está ausente. Si el profesor Márquez hace clase, la probabilidad de que tome la prueba es de 0.70, en tanto que si la clase lo desarrolla el Jefe de Práctica, dicha probabilidad es sólo de 0.10. Si el profesor Márquez falta el 80% de las clases,

a) ¿Cuál es la probabilidad de que haya una prueba en una clase dada?
b) Suponiendo que hubo prueba en una clase determinada, ¿cuál es la probabilidad de que el profesor Márquez haya estado ausente?
Solución

Sea X el evento: “El profesor Márquez falta a clase(no da la clase)”
Sea Y el evento: “Se tomó una prueba en una clase determinada”

a) Se toma una prueba en una clase determinada cuando el profesor Márquez está presente o cuando no lo está. En otras palabras Y = X  Y  X  Y. Esto nos lleva a aplicar el teorema de la probabilidad total.

P(Y) = P(X)P(Y/X) + P(X’)P(Y/X’)
          = (0.80)(0.10) + (0.20)(0.70)
          = 0.22

b) Si se tomó una prueba entonces el evento Y ha ocurrido. La probabilidad de que el profesor Márquez haya estado ausente, sabiendo que hubo una prueba, significa encontrar la probabilidad condicional P(X/Y). Si sólo aplicamos la probabilidad condicional, tendremos



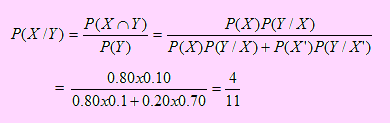
Nota:

Naturalmente P(X/Y) constituye la aplicación del Teorema de Bayes. En muchos casos no es fácil reconocer si para calcular una determinada probabilidad condicional se debe aplicar el teorema de Bayes. En estos casos ayuda muchísimo el trazar un diagrama de árbol. En todo caso, se puede calcular también como una simple aplicación de la probabilidad condicional, como lo hemos hecho en este ejemplo. Sólo recomendamos tomar en cuenta el diagrama para contemplar todas las aristas del problema.

Ejemplo 36

La compañía DataCont está considerando comercializar una calculadora electrónica, una agenda, correo y acceso a Internet, además de acceso telefónico, todo en un mismo equipo celular. De acuerdo con una investigación realizada en un mercado financiero, la probabilidad de que el producto tenga éxito, es 0.80 siempre que CalNet no introduzca aún su nuevo equipo hasta dentro de 6 meses; en tanto que la probabilidad de éxito es de sólo 0.30, si la firma competidora empieza a comercializarlo desde ahora.
Por otro lado, expertos en mercadeo afirman que la probabilidad de que el competidor comercialice el producto es 0.40. Si DataCont tuvo éxito con su producto, ¿cuál es la probabilidad de que la firma competidora haya comercializado su producto?

Solución

Definamos los eventos:
I: “La competencia introduce (comercializa) su nuevo producto”
E: “El producto de DataCont tuvo éxito”



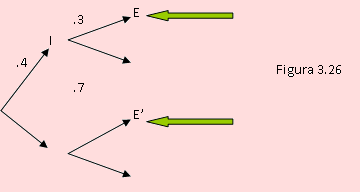
Según el problema, debemos encontrar la probabilidad de la ocurrencia de I, dado que ocurrió E, es decir, P(I/E).

Observe Ud. el diagrama de la figura anterior y coincidirá con nosotros que debemos aplicar el teorema de Bayes.



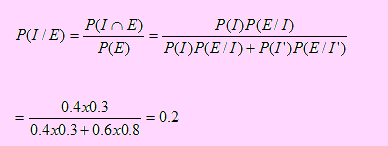
Ejemplo 37

Dany tiene dos bolsas de canicas. La bolsa I contiene 3 bolas rojas y 2 blancas; la bolsa II contiene una bola roja y cuatro blancas. Dany cogió aleatoriamente una bola de la bolsa I y la colocó en la bolsa II. Luego cogió una bola de la bolsa II. Si esta bola es roja, ¿cuál es la probabilidad de que la bola transferida de la bolsa I a la bolsa II, haya sido roja?

Solución

La figura3.27 indica la forma de experimento realizado y la figura 3.28 constituye el diagrama de árbol para dicho experimento.

Según el diagrama



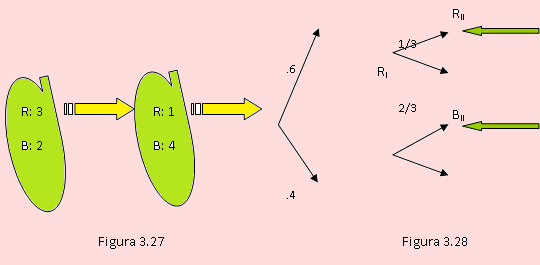
Bi: “La bola extraída de la i-ésima bolsa es blanca”
Ir: “La bola extraída de la i-ésima bolsa es roja”
Debemos encontrar P(R_I /R_II ). Usando probabilidades condicionales tenemos



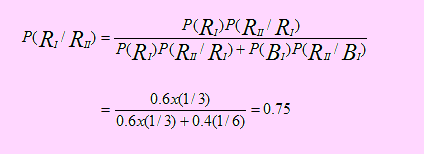
Ejemplo 38

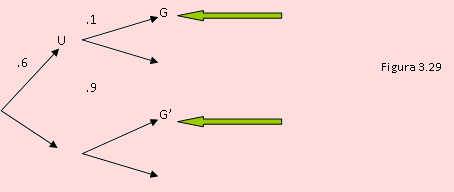
Los registros de la policía local revelan que sólo el 10% de las víctimas de accidentes que llevaban cinturones de seguridad sufrieron heridas graves; en tanto que el 50% de los que no lo usaron sufrieron también serias heridas. La policía estima que el 60% de las personas que viajan en automóviles emplean los cinturones de seguridad. Se llama a la policía para que investigue un accidente en el que una persona resulta seriamente herida. Estime la probabilidad de que llevara puesto el cinturón de seguridad en el momento del choque. El conductor del otro vehículo no sufrió heridas graves. Determine la probabilidad de que este último llevara puesto el cinturón de seguridad.



Solución

Sea U el evento “La persona lleva puesto el cinturón de seguridad”
Sea G el evento “La persona sufre heridas graves”
En el diagrama de la figura anterior se describe gráficamente el problema. Podemos observar que los ramales indicados con la flecha verde nos proporciona la probabilidad de que la persona haya sufrido accidente grave. Es decir
      P(G) = P(U)P(G/U) + P(U’)P(G/U’) = 0.6 x 0.1 + 0.4 x 0.5 = 0.26

a) La primera pregunta corresponde a encontrar la probabilidad de que haya usado cinturón sabiendo que tuvo accidente grave, es decir debemos hallar P(U/G). Usando el Teorema de Bayes, tenemos



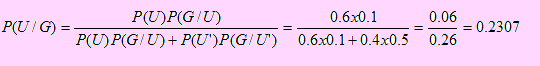
b) En cuanto a la segunda pregunta, debemos hallar la probabilidad de que estuviera puesto el cinturón de seguridad si se sabe que no sufrió accidente grave; esto significa encontrar P(U/G’) lo cual, usando Bayes, tenemos.

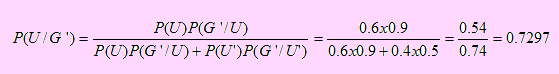
3.7 EVENTOS INDEPENDIENTES

Sea ζ un experimento y Ω el espacio muestral asociado a η. Sean A y B dos eventos de &Omega. Diremos que A y B son eventos independientes si P(A/B) = P(A) ó P(B/A) = P(B) En otras palabras, si la ocurrencia o no de un evento no afecta a la ocurrencia de otro, diremos, que dichos eventos son independientes, en el sentido estadístico. Esto no quiere decir que los eventos sean mutuamente excluyentes.

Teorema

Sea Ω el espacio muestral asociado a ζ. Si A y B dos eventos independientes de Ω. Entonces P(A ∩ B) = P(A) P(B)
En efecto.
De P(A / B) = P(A ∩ B / B),     obtenemos     P(A ∩ B) = P(B) P(A / B) = P(A) P(B).

Puede deducirse también tomando en cuenta la otra forma condicional.

Teorema

Sean A y B dos eventos del espacio muestral Ω, asociados a ζ. Si A y B son eventos independientes, entonces

i) los eventos A y B’ son independientes
ii) los eventos A’ y B son independientes
iii) los eventos A’ y B’ son independientes

Teorema

Sean A, B y C tres eventos del espacio muestral Ω, asociados a ζ. Diremos que los tres eventos son mutuamente independientes si se cumple las siguientes condiciones:

i) P(A ∩ B) = P(A)P(B)
ii) P(A ∩ C) = P(A)P(C)
iii) P(B ∩ C) = P(B)P(C)
iv) P(A ∩ B ∩ C) = P(A)P(B)P(C)

Teorema

Si A₁, A₂, A₃,…, A_n, son eventos independientes dos a dos, entonces P(A₁ ∩ A₂ ∩ A₃ ∩ ; … ∩ A_n ) = P(A₁)P(A₂)P(A₃) …P(A_n)

Ejemplo 39

Si P(A) = 1/6, P(AB) = 1/18, P(B) = 1/3. ¿Son A y B eventos independientes?

Solución

Según el teorema, dos eventos A y B son independientes si P(AB) = P(A)P(B).

Verifiquemos si esto se cumple con los datos:
Como P(AB) = 1/18
Y P(A)P(B) = 1/6 x 1/3 = 1/18.

Entonces A y B son dos eventos independientes.

Ejemplo 40

Una urna contiene 4 bolas blancas y 5 negras. Se extraen sucesivamente y sin reposición dos bolas. Sean los eventos:
A: “La primera bola extraída es negra”
B: “La segunda bola extraída es blanca”
¿Son los eventos A y B, independientes?

Solución

Como en el ejemplo anterior, si P(AB) = P(A)P(B), entonces son eventos independientes. Pues bien, P(A) = 5/9. La ocurrencia de B depende del resultado de la primera extracción. Por ello, debemos trabajar con la probabilidad condicional, P(B/A).

En efecto, P(B / A) = P( A ∩ B) / P(A);   de donde P(A B) = P(A) P(B) = 5/9 x 4/8 = 5 / 18.

Por otro lado, ocurre blanca(es decir, ocurre B) sea por que salió blanca o negra en la primera; es decir, B = A ∩ B ∪ A’ ∩ B.
De donde P(B) = P(AB) + P(A’B)
      = P(A)P(B/A) + P(A’)P(B/A’)
      = 5/9x4/8 + 4/9x3/8 = 4/9
Como P(A)P(B) = 5/9x4/9 = 20/81 y P(AB) = 5/18, entonces A y B no son independientes

Ejemplo 41

Cuatro hombres lanzan, cada uno, un dado. Cuál es la probabilidad de que:
a) cada uno obtenga un cuatro
b) cada uno obtenga un número par de puntos
c) todos obtengan el mismo número de puntos

Solución

a) Sea Ai el evento “El i-ésimo hombre obtiene un cuatro”
Para que cada uno obtenga un cuatro, debe ocurrir el evento compuesto; A₁A₂A₃A₄
Puesto que el resultado del lanzamiento del segundo hombre no depende de lo que haya ocurrido con el resultado del primero, entonces ambos eventos son independientes. Esto es cierto con los cuatro hombres. Por lo que

P(A₁A₂A₃A₄ ) = P(A₁)P(A₂) P(A₃)P(A₄) = (1/6)⁴ = 1/1296

b) Sea Ai el evento “El i-ésimo hombre obtiene un número par de puntos”
En este caso también los resultados de cada lanzamiento son independientes uno de otro.
Sólo que, a diferencia de a), la probabilidad individual cambia ya que P(Ai) = 3/6 =1/2.
Luego P(A₁A₂A₃A₄ ) = P(A₁)P(A₂) P(A₃)P(A₄) = (1/2)4

c) Sea B el evento “Los cuatro hombres obtienen el mismo número”
Si lanza el dado el primer hombre, la probabilidad de que obtenga un número cualquiera, es 1. Ahora bien, supongamos que el número obtenido es x, para x = 1, 2, 3, 4, 5, 6. La probabilidad de que el segundo obtenga dicho número es 1/6; de que cada uno de los tres obtenga dicho número es 1/6. Luego, la probabilidad de que los tres hombres obtengan el número x, obtenido por el primero será (1/6)³. Ejemplo 42

Ocho boletos numerados: 111, 121, 122, 122, 211, 212, 212, 221 son colocados en una bolsa y luego revueltas. Se va a escoger uno al azar. Si se definen los siguientes eventos:
A: “El primer dígito del boleto escogido es 1”
B: “El segundo dígito en el boleto escogido es 1”
C: “El tercer dígito en el boleto escogido es 1”
a) ¿Son los eventos A, B y C independientes entre sí?
b) Calcular P(A ∪ B/B ∩ C)

Solución

a) Para que A, B y C, sean independientes entre sí, se debe cumplir
i) P(AB) = P(A) P(B)
ii) P(AC) = P(A) P(C)
iii) P(BC) = P(B) P(C)

Según los datos, P(A) = 1/2 ; P(B) = 1/2 ; P(C) = 1/2
Por otro lado P(AB) = 1/8; P(AC) = 2/8; P(BC) = 2/8

Verificando las igualdades, i), ii) y iii), encontramos que los eventos A y C son independientes, así como B y C, pero A y B no son independientes; por tanto los tres eventos no son independientes entre sí.

b) P(A ∪ B / B ∩ C) = P( (A ∪ B) ∩ (B ∩ C)) / P(B ∩ C) = P(ABC ∪ BC) / (2/8) )= (1/8 + 2/8 - 1/8) / (2/8) = 1

Ejemplo 43

Suponga que un misil tiene la probabilidad 1/2 de destruir su blanco y la probabilidad 1/2 de no destruirlo. Suponiendo que el lanzamiento de los misiles forman pruebas independientes, determínese el número de misiles que debe lanzarse para conseguir que la probabilidad de destruir el blanco sea por lo menos de 0.99. Solución



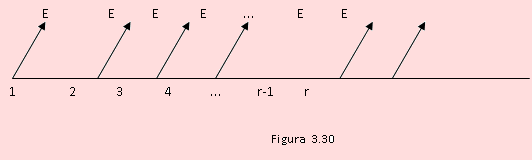
Supongamos que es necesario realizar “r” pruebas para alcanzar por lo menos 0.99 de probabilidad de destruir el blanco.
Si D el evento “El blanco queda destruido” entonces

D = E ∪ FE ∪ FFE ∪ FFFE ∪ FFF...FE, entendiendo que en el último término de la igualdad, ocurren “r-1” fracasos y el “r-ésimo” es exitoso.
Por los datos del problema, P(D) ≥ 0.99
De la igualdad, P(D) = P(E) + P(FE) + P(FFE) + P(FFFE) + ... + P(FFF...FE)
Es suficiente que

0.99 ≤ 1/2 +(1/2)(1/2)+(1/2)2(1/2)+(1/2)3(1/2)+…(1/2)(r-1)(1/2)
        ≤ 0.5 + 0.25 + 0.125 + 0.0625 + 0.03125 + 0.015625 + 0.0078125
lo que corresponde al lanzamiento de 7 misiles, por lo menos.

Ejemplo 44

¿Cuántas personas deben escoger una carta, cada una de diferente baraja, para tener una probabilidad mínima de 0.90 de que, por lo menos se escoja un as?

Solución

Bien sabemos que una baraja de cartas tiene 52 cartas. Hay cuatro ases. Luego, si una persona cualquiera toma una carta de una baraja, la probabilidad de que extraiga un as, es 4/52 = 1/13.

Sean los eventos
A: “Una determinada persona extrae un as”
B: “Las otras personas no extraen un as”
C: “Se obtiene por lo menos un as”

Según el ejemplo, con todas las personas se debe extraer, por lo menos un as. Esto quiere decir que, si fueran 10 personas, sólo una de ellas podría extraer un as y las otras no, que dos de ellas extraigan un as y las otras no, o que haya 8 personas que extraen un as y las otras dos, no; etc. En otras palabras debe ocurrir el siguiente evento.

Una sola persona extrae un as con P(A) = 1/13
Dos personas extraen por lo menos un as según el evento C = AB + BA + AA con
P(C) = P(AB) + P(BA) + P(AA) = C(2,1)(1/13)(12/13)+C(2,2)(1/13)²= 2x1/13 x 12/13+(1/13)²

Con tres C = ABB + BAB + BBA + AAB + ABA + BAA + AAA, por lo menos un as.

En este caso



desarrollando esta serie debemos encontrar el valor de n.
Una manera de resolverlo sin usar series de potencia es mediante una hoja de cálculo con lo cual se puede encontrar el valor de n = 28.

Ejemplo 45

Se dispara cada uno de los fusiles A, B y C; las probabilidades de dar en el blanco es 0.15, 0.25 y 0.35, respectivamente. Calcular la probabilidad de que
a) al menos uno de los tres dé en el blanco
b) acierte uno sólo

Solución

Sean los eventos
A: “El fusil A da en el blanco”           con P(A) = 0.15
B: “El fusil A da en el blanco”           con P(B) = 0.25
C: “El fusil A da en el blanco”           con P(C) = 0.35

a) Sea X: “Uno de los tres fusiles A, B ó C da en el blanco”
Debemos recordar que el hecho que un fusil dé o no en el blanco, no afecta a los otros.
Entonces P(X ) = P(A  B  C ) = P(A)+P(B)+P(C) –P(AB)-P(AC)-P(BC)+P(ABC)

Pero también, P(X) = 1 – P((A  B  C)’) = 1 – P(A’)P(B’)P(C’)
          = 1 – (0.85)(0.75)(0.65)
          = 0.585625

b) Sea X: “Sólo uno de los tres fusiles acierta en el blanco”
En este caso X = AB’C’ + A’BC’ + A’B’C, de donde
    P(X) = P(A)P(B’)P(C’) + P(A’)P(B)P(C’) + P(A’)P(B’)P(C)
          = 0.15x0.75x0.65 + 0.85x0.25x0.65 + 0.85x0.75x0.35
          = 0.434375

Ejemplo 46

Un antiguo teatro tiene un solo proyector. La bombilla del proyector funciona; la probabilidad de que se queme antes de terminar la película es 0.40. De las 20 lámparas de reserva, una de ellas tiene un defecto no visible. De las restantes, la probabilidad de que se quemen antes de terminar la película es 0.20.
a) ¿Cuál es la probabilidad de que se queme la lámpara en funcionamiento y seleccionada al azar una extra, se escoja la lámpara defectuosa?
b) ¿Cuál es la probabilidad de que se queme la lámpara en funcionamiento y seleccionada una perfecta para reemplazarla, se queme a su vez antes de terminar la película?

Solución

Definamos los eventos:
A: “La lámpara en funcionamiento se quema antes de terminar la película”
B: “La lámpara seleccionada de reserva es la defectuosa”
C: “La lámpara seleccionada no defectuosa, se quema antes de terminar la película”
a) Si definimos el evento D: “Se quema la lámpara en funcionamiento y se escoge de las de reserva, la defectuosa”, entonces D = A  B. Debemos hallar P(D). Como A y B son eventos independientes y como P(A) = 0.40 y P(B) = 1/20, tenemos
P(D) = P(A ∩ B) = P(A)P(B) = 0.40 x (1/20) = 0.02

b) Aquí se pide encontrar P(A  C). Como en el caso a), el hecho de que la lámpara en funcionamiento se queme o no, en nada influye a que cualquiera de las 19 perfectas de reserva, se queme también antes de terminar la película. Por ello A y C son independientes. Según esto P(A) = 0.40, por datos; la ocurrencia de C implica la ocurrencia de dos subeventos: Seleccionar una perfecta de los de la reserva, cuya probabilidad es 19/20, y que se queme antes de terminar la película, con probabilidad 0.20. Por lo que
P(A ∩ C) = P(A)P(C) = 0.40 x 19/20x 0.20 = 0.076.

Ejemplo 47

Una persona A padece una cierta enfermedad; consultado los médicos, las opiniones están en la relación de 9 a 7 en contra de que la persona viva cinco años más. Otra persona B tiene 45 años, y las opiniones están en la relación 3 a 2 en contra de que viva hasta los 5años más. Hallar la probabilidad de que cuando menos una de estas personas viva cinco años más.

Solución

Sean los eventos:
A: “La persona A, viva cinco años más” y
B: “La persona B, viva cinco años más”;
C: “Por lo menos una de las dos personas vive cinco años más”

Debemos encontrar la probabilidad del evento C, el cual lo definimos como C = A ∪ B. En efecto, P( C) = P(A ∪ B) = P(A) + P(B) – P(A ∩ B), en donde A y B son independientes.

P( C) = 7/16 + 2/5 – (7/16)(2/3) = 53/80 = 0.6625

Ejemplo 48

Una pieza de un equipo electrónico tiene tres partes esenciales. Anteriormente la parte A ha fallado el 20% del tiempo; la parte B, 40% del tiempo y la parte C, 30% del tiempo. La parte A opera independientemente de las partes B y C. Las partes B y C están interconectadas, de tal manera que la falla de cualquiera, afecta a la otra; por ello, cuando falla la parte C, dos de cada tres veces puede también fallar la parte B.
Supongamos que por lo menos dos de las tres partes deben operar para permitir el funcionamiento del equipo. ¿Cuál es la probabilidad de que el equipo funcione?

Solución

Sean los eventos:
A: “Falla la parte A” P(A) = 0.2
B: “Falla la parte B” P(B) = 0.4
C: “Falla la parte C” P(C) = 0.3
Además se sabe que P(B/C) = 2/3
Sea D el evento “Funcionan por lo menos dos de las partes”
Decir que funcionan, por lo menos dos, significa que funcionan dos o tres.

- Funcionan dos partes puede ser expresado por: A’ ∩ (B’ ∪ C’)
- Funcionan tres partes puede ser expresado por: A’ ∩ B’ ∩ C’ Luego D = A’ ∩ (B’ ∪ C’) ∪ A’ ∩ B’ ∩ C’

Los dos eventos de la derecha son excluyentes, por lo que
P(D) = P(A’ ∩ (B’ ∪ C’) ) + P( A’ ∩ B’ ∩ C’ )
P(A’ ∩ (B’ ∪ C’) ) = P([A ∪ (B ∩ C)]’ ) = 1 – { P(A) + P(B ∩ C) – P(A ∩ (B ∩ C))}
          = 1 – { 0.2 + P(C)P(B/C) – P(A)P(C)P(B/C)} = 0.64
P(A’ ∩ B’ ∩ C’ ) = 1 – P(A ∪ B ∪ C ) = 1 – {P(A) + [P(B &∪ C)] – P(A ∩ ( B ∪ C)}       =1 – {0.2 + [0.4 + 0.3 – 0.2(0.3)(2/3)] – (P(AB)+P(AC)-P(ABC))}
            = 0.2

Luego P(D) = 0.64 + 0.2 = 0.84

Ejemplo 49

La probabilidad de que un cazador dé en el blanco en un disparo cualquiera es 0.40.
a) ¿Cuál es la probabilidad de que falle en cuatro tiros consecutivos?
b) ¿Cuál es la probabilidad de que dé en el blanco por lo menos una vez en 4 tiros consecutivos?
c) ¿Cuántos tiros debe disparar para tener una seguridad aproximadamente de 0.95 de dar en el blanco por lo menos una vez?

Solución

Sea B el evento: “El cazador da en el blanco con un disparo”.
a) Falla cuatro veces si ocurre el evento compuesto A = B’ ∩ B’ ∩ B’ ∩ B’. Como los disparos son independientes uno de otro,
P(A) = P(B’ ∩ B’ ∩ B’ ∩ B’) = [P(B’) ]⁴ = 0.6⁴ = 0.1296

b) Sea C el evento “Da en el blanco por lo menos una vez en cuatro tiros”
De acuerdo a la definición del evento C, podemos decir que C’ es el evento “Da en el blanco cero veces”. Y según la definición de eventos, C ∪ C’ = Ω.
Ahora bien, P(C) =P(A) = 0.1296, obtenido en el inciso a).
Por ello, P(C’) = 1 – P(C) = 1 – 0.1296 = 0.8704

c) Si Bi es el evento “Da en el blanco en i-ésimo disparo”, entonces se debe cumplir lo siguiente
P(B I ó B i  B 2 ó B I  B 2 B i ó B I  B 2  B 3  B 4 ó …) = 0.95
Desarrollando por partes el primer miembro, tenemos
En un tiro: P(B I) = 0.4
En dos tiros: P( B I B 2 ‘ó B I ‘B 2 ó B I B 2) = 2(0.4(0.6)) + 0.16 = 0.64
En tres tiros: Sumando las siguientes opciones, tenemos 0.784.
3x P(Dé una vez en el blanco y los otros no) = 3(0.4)(0.36) = 0.432
3x P(Dé dos veces en el blanco y uno de ellos no) = 3(0.16)(0.6) = 0.288
P(Dé las tres disparos en el blanco) = (0.4)(0.4)(0.4) = 0.064

Nota:

Si definimos el evento R: “En tres disparos dar cero veces en el blanco” entonces P(R) = 0.6(0.6)(0.6) = 0.216. De donde P(R’) = P(Dar en el blanco por lo menos una vez en tres disparos) = 1 – P(R) = 0.784
En cuatro disparos: Usando la nota anterior:
La probabilidad pedida será = 1 – (0.6)4 = 1 - 0.1296 = 0.8704
En cinco disparos tendremos:
La probabilidad pedida será = 1 – (0.6)5 = 1 - 0.07776= 0.92224
En seis disparos tendremos:
La probabilidad pedida será = 1 – (0.6)6 = 1 - 0.046656= 0.953344
Con lo cual concluimos que el número de disparos necesarios para dar en el blanco, por lo menos una vez, debe ser 6 de suerte que se tenga la probabilidad de 0.95 de que eso ocurra.

Ejemplo 50

Un sistema consiste de cuatro componentes: A, B, C y D. Las probabilidades de falla son 0.01, 0.02, 0.10 y 0.10 para A, B, C y D, respectivamente. Si para el funcionamiento del sistema son necesarios los componentes A y B y al menos uno de los componentes C o D, ¿cuál es la probabilidad de que el sistema funcione?

Solución

Sea F el evento “El sistema funciona”. Este evento se produce si ocurre el siguiente evento compuesto: A ∩ B ∩ ( C ∪ D ).
En consecuencia P( F ) = P(A ∩ B ∩ ( C ∪ D ))
          = P(A) P(B) P( C ∪ D )
          = (0.99)(0.98)[1 – P(C’  D’)]           = (0.99)(0.98)(1 – 0.01)
          = 0.960498.

Ejemplo 51

Considere tres urnas. La urna I contiene una bola blanca y dos negras; la urna II contiene tres bolas blancas y dos negras; la urna III contiene dos blancas y tres negras. Se extrae una bola de cada urna. ¿Cuál es la probabilidad de que entre las bolas extraídas haya
i) una blanca y dos negras
ii) por lo menos dos negras
iii) más negras que blancas
Solución

Supongamos que
Bi es el evento “Se extrae una bola blanca de la i-ésima urna”
Ni es el evento “Se extrae una bola negra de la i-ésima urna”
Definamos también los eventos X, Y y Z de la siguiente manera:
X: “Se extrae una bola blanca y dos negras”
Y: “Se extrae por lo menos dos bolas negras”
Z: “Se extrae más negras que blancas”

i) El evento X puede ser definido como X = B1 N2 N3 + N1 B2 N3 + N1 N2 B3
P(X) = P(B1 N2 N3 ) + P(N1 B2 N3 ) + P(N1 N2 B3 ) = 1/3 (2/5)(3/5) + (2/3)(3/5)(3/5) + (2/3)(2/5)(2/5)= 0.42666667
ii) El evento Y se define como Y = B1 N2 N3 + N1 B2 N3 + N1 N2 B3 + N1 N2 N3
Por lo menos dos negras, significa que puede obtenerse dos o tres negras. Luego
P(X) = P(B1 N2 N3 ) + P(N1 B2 N3 ) + P(N1 N2 B3 ) + P(N1 N2 N3 ) = 1/3 (2/5)(3/5) + (2/3)(3/5)(3/5) + (2/3)(2/5)(2/5)+(2/3)(2/5)(3/5)= 0.58666667 iii) El evento Z es equivalente al evento Y ya que las únicas formas en las que el número de bolas negras extraídas es mayor que las bolas blancas extraídas es cuando Z = Y
Luego P( Z ) = P( Y ) = 0.5866667

Ejemplo 52

Una urna contiene 12 bolas, de las cuales 7 son negras y 5 son blancas. Se extraen dos bolas y se devuelven a la urna. Se vuelven a sacar dos bolas y se devuelven a la urna. El experimento continúa hasta hacer 5 extracciones.

a) ¿Cuál es la probabilidad de extraer dos bolas negras en cada uno de los tres primeros experimentos y una pareja de una blanca y una negra en los últimos dos experimentos?
b) ¿Cuál es la probabilidad de extraer dos bolas negras tres veces y las otras dos veces, dos blancas?



Solución

El esquema de la figura anterior nos muestra la urna con 5 bolas blancas y 7 negras, y las cinco extracciones realizadas, con las diferentes posibilidades de pares de bolas a extraerse.
a) Sea X el evento: “Obtener dos negras en las tres primeras extracciones y una blanca con una negra en las dos últimas extracciones”. En el esquema también apreciamos en color azul los eventos que deben ocurrir para que ocurra X. Esto implica que
P(X) = P(NN ∩ NN ∩ NN ∩ (NB ∪ BN)) = [(7/12)(6/11)]³[(5/12)(7/11)+(7/12)(5/11)]² = (7/22)³ (35/66)²

b) Sea R el evento “Obtener dos bolas negras tres veces y dos blancas las otras dos”.
La ocurrencia de R puede darse en varias instancias: {NN NN NN xx xx }, {NN NN xx NN xx }, {xx NN xx NN NN }, entre otras. En cada uno de estas secuencias “xx” representa cualquier combinación de B con N. El número total de estas instancias es 10.
Obengamos la probabilidad de una cualquiera de ellas: P(R) = P({NN NN NN xx xx }) = 10 x [(7/12)(6/11)]³ [(5/12)(4/11)]².

Ejemplo 53

La producción diaria de una máquina que produce una pieza muy complicada da las siguientes probabilidades para el número de piezas producidas:
p({1}) = 0.10, p({2}) = 0.30, p({3}) = 0.60.
Por otro lado, la probabilidad de producir piezas defectuosas es 0.3. Las piezas defectuosas pueden aparecer independientemente durante el proceso de producción. En un día determinado, ¿cuál es la probabilidad de no se hayan producido piezas defectuosas?

Solución

Sean los eventos
A: “La máquina produce una pieza complicada” &nbsp: &nbsp: &nbsp: &nbsp: P(A) = 0.1
B: “La máquina produce dos piezas complicadas” &nbsp: &nbsp: &nbsp: &nbsp: P(B) = 0.3
C: “La máquina produce tres piezas complicadas” &nbsp: &nbsp: &nbsp: &nbsp: P(C) = 0.6
N: “La máquina produce una pieza no defectuosa” &nbsp: &nbsp: &nbsp: &nbsp: P(N) = 0.97
D: “La producción del día no registra defectuosos”

Debemos hallar.
Si se produce una pieza entonces P(N) = P(A)P(N) = 0.1x0.97 = 0.097

Si se produce dos piezas entonces P(N) = P(A)P(N)P(N) = 0.1x0.97x0.97
        = 0.282270 Si se produce tres piezas entonces P(N) = P(A)P(N)3 = 0.1x0.973
        = 0.5476038 En consecuencia la probabilidad de que no se produzca piezas defectuosas en un día determinado es 0.097 + 0.282270 + 0.5476038 = 0.92687

Ejemplo 54

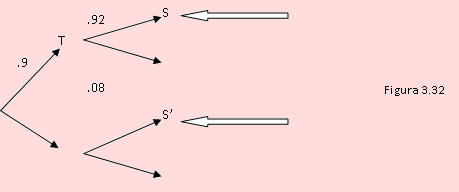
Si una máquina que produce engranajes está trabajando correctamente, el 92% de las piezas satisfacen las especificaciones. Si la máquina no trabaja bien, sólo el 60% de los engranajes producidos satisfacen las especificaciones. La máquina trabaja correctamente el 90% del tiempo. Se seleccionan 4 engranajes y todos satisfacen los requerimientos. ¿Cuál es la probabilidad de que la máquina no haya estado trabajando bien?



Solución

Sean los eventos
T: “La máquina trabaja correctamente”
S: “El engranaje producido satisface los requerimientos”

Según los datos debemos encontrar P(T’ / S ), es decir, la probabilidad de que no haya estado trabajando correctamente, dado que los engranajes producidos satisfacen los requerimientos.

Por el teorema de Bayes tenemos



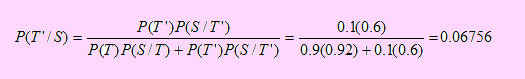
Ejemplo 55

Un fabricante está considerando comprar un lote grande piezas de un proveedor. El fabricante estima la proporción de piezas defectuosas en el lote de la siguiente forma:

 

Proporción de piezas defectuosas (π)	Probabilidad (P(π)
0.10	0.20
0.15	0.30
0.25	0.50

Suponga que se elige tres piezas al azar del lote
a) ¿Cuál es la probabilidad de que las tres piezas sean de calidad aceptable?
b) Si las tres piezas resultaron de calidad aceptable, ¿cuál es la probabilidad de que el lote contenga 10% de piezas defectuosas?

Solución

Sean los eventos:
P1: “La pieza proviene de la proporción de 10% defectuosas”
P2: “La pieza proviene de la proporción de 15% defectuosas”
P3: “La pieza proviene de la proporción de 25% defectuosas”
A : “La pieza es de calidad aceptable”
T : “Las tres piezas son de calidad aceptable”
El diagrama de árbol de la figura 3.33 muestra las características del problema



En este diagrama los ramales del primer nodo sólo toman en cuenta la proporción de defectuosos de cada sublote más no los no-defectuosos; que serán de 90%, 85% y 75%, respectivamente. De acuerdo al problema, debemos hallar primero, en a) la probabilidad de que sean aceptables las tres piezas; es decir P(A) y en b) debemos hallar P(P1/A); es decir , la probabilidad de que las piezas provengan del grupo de los de 10%.
Por otro lado, para los propósitos del problema, no interesan. Puesto que se eligen tres piezas aleatoriamente y se desea que las tres sean aceptables, tenemos entonces la repetición del experimento “Elegir una pieza” tres veces. Los eventos que se generan son eventos independientes por lo que el resultado que obtengamos debe ser multiplicado tres veces.

a) Tomando en cuenta las consideraciones anteriores, tenemos
P(T) = [ P(A) ]³
= (P(P1)P(A/P1) + P(P2)P(A / P2) + P(P3) P(A / P3))³ = 0.105625.

b) Según lo dicho en los considerandos,



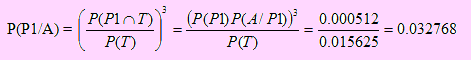
Ejemplo 56

De tres eventos A1, A2, A3 se sabe que son mutuamente independientes; que la probabilidad de la ocurrencia del primero es el doble de la ocurrencia del segundo; que la probabilidad de la ocurrencia simultánea de los dos primeros eventos es 0.02; y que la probabilidad de que ocurra al menos uno de ellos, es 0.64. Calcular la probabilidad de la ocurrencia de cada uno de dichos eventos.

Solución

Debemos encontrar P(A1), P(A2) y P(A3 ).
Por los datos del problema sabemos que:
P(A1) = 2 P(A2) y que
P(A1 ∩ A2) = 0.02
Puesto que los eventos son mutuamente independientes entonces
P(A1 ∩ A2) = 0.02 = P(A1) P(A2) = P(A1) P(A2) = 2[P(A2)]².
De donde P(A2) = 0.1 y también P(A1) = 0.2
Por otro lado, el evento “Por lo menos uno” con tres eventos se expresa como A1 ∪A2 ∪A3 . Luego P(A1 ∪ A2 ∪ A3 ) = 0.64. Si por lo menos uno tiene probabilidad de ocurrencia de 0.04 entonces la probabilidad de que ninguno ocurra(ocurra cero) es 0.36. En otras palabras
Si P(A1A2A3 ) = 0.64 , entonces P(A1‘ A2‘A3 ‘) = 0.36. Usando esto último, tenemos
0.36 = P(A1‘ ∩ A2‘ ∩ A3 ‘) = P(A1‘) P(A2‘ ) P(A3 ‘) = 0.8x0.9x P(A3 ‘), simplificando y despejando, obtenemos P(A3 ‘) = 0.5

Ejemplo 57

Un aparato tiene cuatro válvulas que funcionan independientemente, sus probabilidades de falla son respectivamente, 0.1, 0.2, 0.3 y 0.4 para la primera, segunda, tercera y cuarta válvula. Se sabe que dos de estas válvulas han fallado. Hallar la probabilidad de que hayan fallado la primera y la segunda válvulas.

Solución

Sea F el evento “Una válvula determinada falla” y
N, “Una válvula determinada no falla”
Con cuatro válvulas en las que dos de ellas fallen, podemos tener las siguientes posibles combinaciones, donde el orden representa el número de válvula:
F F N N,       F N F N,       F N N F,       N F N F,       N F F N,       N N F F

Si definimos al evento A como “Fallan dos de las cuatro válvulas” , entonces
A = { F F N N, F N F N, F N N F, N F N F, N F F N, N N F F } , y si ahora definimos a B como el evento B = { FFNN}, de acuerdo a la pregunta, debemos encontrar la probabilidad de que hayan fallado las dos primeras válvulas, si se sabe que han fallado dos de las cuatro válvulas; es decir, P(B/A).

Encontremos primero P(A).

P(A) = P({FFNN})+P({FNFN})+P({FNNF})+P({NFNF})+P({NFFN})+P({NNFF})

= 0.1x0.2x0.7x0.6+0.1x0.8x0.3x0.6+0.1x0.8x0.7x0.4+0.9x0.2x0.30.6+0.9x0.8x.3x.4
=0.2144

Usando el teorema de Bayes, tenemos P(B / A) = P(A ∩ B / A) = P(B) / P(A) = (0.1)(0.2)(0.7)(0.6) / 0.2144 = 0.0391791

Ejemplo 58

Se lanza una moneda repetidamente hasta que salga cara. Si Ud. es la persona que juega, ¿cuál es la probabilidad de que obtenga cara alguna vez?

Solución

Este es un modelo de experimentos que se repiten indefinidamente y que generan por tanto, espacios muestrales infinitos.
Sea A el evento “Ganar el juego”



El esquema de la figura 3.34 refleja la posible secuencia del juego.

Cada vez que salga sello, S, se vuelve a lanzar la moneda. En el momento que sale cara, termina el juego.
Luego, algunos de los elementos del espacio muestral Ω son
Ω = {C, SC, SSC, SSSC, SSSSC, SSSSSC, ......}, sin duda, un espacio muestral infinito.
Como el evento A se define como “Ganar el juego”, entonces A = Ω. Encontremos la probabilidad de A (suponemos que debe ser 1, por lo que ya sabemos).
Como se trata de eventos independientes, entonces



Nota:

Puesto que se trata de experimentos aleatorios infinitos, el espacio muestral , asociado a dichos experimentos, debe ser también infinito, salvo si algún(os) resultado(s) se repitiera(n) indefinidamente.
Del mismo modo, podemos estar interesados en evaluar la probabilidad de eventos infinitos, como es el caso de este problema. Para hallar dicha probabilidad debemos resolver una suma de términos que cae en el terreno matemático de las series de potencia; sean estas finitas o infinitas.
Según la evaluación de series infinitas en matemática se sabe que, bajo ciertas condiciones, como que la razón “r”, de la serie debe ser r  ½ , en cuyo caso


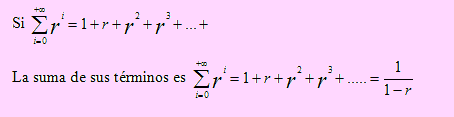
Por ello en el problema anterior hemos hecho r = ½.
<
Ejemplo 59

Se trata ahora de lanzar un dado y una moneda. Si sale un seis, se gana y termina el juego, de otra manera, se lanza una moneda. Si sale cara, se pierde y termina el juego; si sale sello se vuelve a tirar el dado. Esto se repite indefinidamente hasta ganar(que salga un seis). Encuentre la probabilidad de ganar el juego.

Solución

Globalmente tomemos en cuenta que primero se lanza el dado y después la moneda. Esto se repite indefinidamente. El esquema siguiente muestra el experimento.



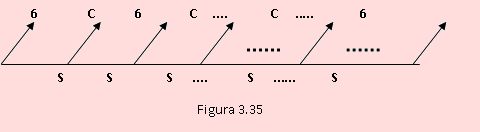
Cada vez que se lanza la moneda, el resultado del lanzamiento del dado fue un número diferente de 6.
Sean los eventos
A: “Sale un 6”         P(A) = 1/6
N: “Sale un número diferente de 6”       P(N) = 5/6
S: “Sale sello”           P(S) = 1/2
C: “Sale cara”             P(C)= ½
G: “Ganar el juego”             P(G) es lo que debemos encontrar
El espacio muestral está definido como
Ω = {A, NC, NSA, NSNC, NSNSA, NSNSNC, NSNSNSA, ...}
El evento G contendrá sólo a los elementos que terminan en A y contengan series de NS, es decir
G = {A, NSA, NSNSA, NSNSNSA, ...}
Luego



Ejemplo 60

Tres jugadores A, B y C, lanzan al aire un dado, en ese orden. Empieza el jugador A. Gana el jugador que obtiene un 3 ó un 4. El juego continúa hasta que uno de ellos gane. Encuentre la probabilidad de ganar de cada uno de ellos.

Solución

Sean los eventos
A: “Gana el jugador A”
B: “Gana el jugador B”
C: “Gana el jugador C"



Nomenclatura:

G_A; significa que el jugador A gana dicha jugada al haber obtenido un 3 ó un 4.
G_B significa que el jugador B gana dicha jugada al haber obtenido un 3 ó un 4.
G_C significa que el jugador C gana dicha jugada al haber obtenido un 3 ó un 4.
Según el problema, las probabilidades de ganar de cada uno de ellos, cada vez que juegan es
P(G_A ) = 2/6 = 1/3
P(G_B ) = 2/6 = 1/3
P(G_C ) = 2/6 = 1/3
A, B y C pueden ganar en cualquiera de las siguientes situaciones:
A={ G_A , P_A P_B P_C G_A , P_A P_B P_C P_A P_B P_C G_A , .... }
B={ P_A G_B , P_A P_B P_C P_A G_B , P_A P_B P_C P_A P_B P_C P_A G_B , .... }
C={ P_A P_B G_C , P_A P_B P_C P_A P_B G_C , P_A P_B P_C P_A P_B P_C P_A P_B G_C , .... }
Tomando probabilidades, la probabilidad de que gane A



Ejemplo 61

Un jugador arroja dos dados. Si en su primera jugada obtiene un total de 7 ú 11 puntos, gana el juego, si en esta primera jugada obtiene un total de 2, 3 ó 12, pierde el juego, por el contrario, si obtiene un total de 4, 5, 6, 8, 9 ó 10 puntos, continúa jugando hasta obtener el puntaje que obtuvo en la primera jugada, o hasta obtener un total de 7. En el primer caso gana y en el segundo(obtener un total de 7) pierde el juego. ¿Cuál es la probabilidad de que gane?



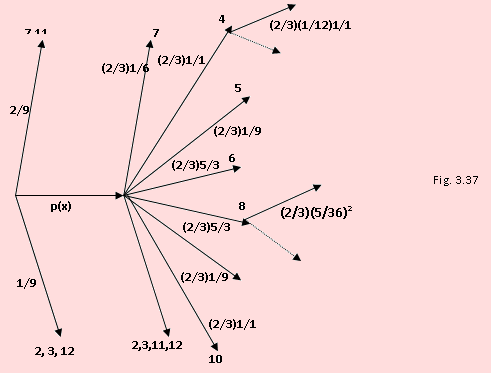
Solución

El esquema de la figura 3.37 pretende reflejar lo que puede suceder al realizarse el juego.


Describámoslo:
En el primer lanzamiento puede salir:
i) Un 7 ú 11 con probabilidad = 2/9, en cuyo caso se gana
ii) Un 2, 3, ó 12 con probabilidad = 1/9, en cuyo caso se pierde
iii) Un 4, 5, 6, 8, 9 ó 10 con probabilidad = 1/12, 1/9, 5/36, 5/36, 1/9, 1/12; opciones en las que se sigue jugando hasta obtener uno de estos números en cuyo caso se gana. Y se pierde cuando sale un 7. Si salió un 4, p(x) = 1/12, etc.

Entremos en detalle:

Si en la primera salió un 4 con p(4)=1/12, el segundo cuatro puede salir en la segunda jugada, con p(x) = (1/12)(1/12); saldrá en la tercera siempre que en la segunda no salga un 7, esto ocurre con p(x) = (1/12)(9/12)(1/12); es decir, la probabilidad de que salga en la primera un 4, es 1/12, de que no salga un 4 en la segunda es 11/12 menos la probabilidad de que no salga el 7 (11/12 – 1/6 = 9/12) y que salga el segundo 4 en la tercera, con probabilidad 1/12.
La serie que se genera para ganar con 4 es la siguiente:






Ejemplo 62

Jaimito se presenta a un examen de competencia de salto alto e intenta pasar una determinada altura. Para ello Jaimito puede repetir el salto varias veces hasta lograr el éxito. Suponga que la probabilidad de tener éxito en un intento cualquiera es de 0.1 y que los intentos son eventos independientes. ¿Cuál es la probabilidad de que
a) Le tome más de 4 intentos?
b) Le tome más de 10 intentos?
Solución

Sea A el evento “Jaimito pasa limpiamente la altura exigida, en el k-ésimo intento, por lo menos”
Designaremos con E cuando hay éxito y con F cuando hay fracaso.

Según esto, el espacio muestral viene dado por
Ω = {E, FE, FFE, FFFE, FFFFE, FFFFFE, ... }

3.8 PROBLEMAS PROPUESTOS

1. Una firma de gran prestigio está interesada en elevar la calidad de los productos que ensambla. Por esta razón luego de un proceso de ensamble de un lote del día, todos ellos se someten a revisión. Se identifican tres tipos de defectos como: defectos críticos, defectos mayores y defectos menores. Se designa a una empresa de envíos por correo, quienes se encargan de clasificarlos en a, b y c, respectivamente. Al analizar los datos se obtienen los siguientes resultados:

 

Aparatos que sólo tienen defectos críticos	2%
Aparatos que sólo tienen defectos mayores	5%
Aparatos que sólo tienen defectos menores	7%
Aparatos que sólo tienen defectos críticos y mayores	3%
Aparatos que sólo tienen defectos críticos y menores	4%
Aparatos que sólo tienen defectos mayores y menores	3%
Aparatos que sólo tienen los tres tipos de defectos	1%

a) ¿Qué porcentaje refrigeradoras no tienen defectos?
b) Los aparatos con defectos críticos o mayores deben reemplazarse para un nuevo ensamble. ¿Qué porcentaje corresponde a esta categoría?
2. Usando diagramas de Venn muestre la veracidad de las siguiente propiedades:
Leyes asociativas: A ∩ (B ∩ C) = (A ∩ B) ∩ C
A ∪ (B ∪ C) = (A ∪ B) ∪ C
Leyes distributivas: A ∪ (B ∩ C) = (A ∩ B) ∪ (A ∩ C)
A ∩ (B ∪ C) = (A ∪ B) ∩ (A ∪ C)
Si A está enB, entonces A ∩ B = A
Si A está contenido en B, entonces A ∪ B = A
Si A ∩ B = φ, entonces A no está contenido en B
Si A está contenido en B y B está contenido en C, entonces A está contenido en C
3. Describa el espacio muestral para este experimento

a) La oficina de la calidad de DiskitSA, fabricante de discos ópticos lleva a cabo pruebas de validación, de un lote de producción diaria. La prueba se realiza de uno en uno a la vez y se marcan ya sea como defectuoso o como no defectuoso. Esto continúa hasta encontrar dos artículos defectuosos o cuando se han probado cinco artículos.
Describa el espacio muestral para cada uno de los siguientes experimentos:
b) Un lote de 120 tapas de tanque de gasolina para un determinado vehículo contiene varias defectuosas debido a un problema con el material empleado. Se selecciona tres tapas al azar(sin reemplazo) y se inspecciona con cuidado siguiendo un procedimiento de ajuste
c) Una tarjeta de video formado por 10 piezas fundidas a cierta temperatura, contiene una unidad defectuosa y nueve en buen estado. Se selecciona cuatro piezas al azar(sin reposición) y se inspecciona.

4. Se desea determinar el número de maneras de asignar trabajadores aptos para la construcción al primer turno. Se cuenta con 15 hombres que pueden servir como operadores del equipo de relleno, 8 que pueden desempeñarse como personal de armado y 4 que pueden ser asistente. Si el turno requiere de 6 operadores, 2 trabajadores de armado y un asistente, ¿de cuántas maneras puede formarse el primer turno?

5. DrySA. es una empresa que fabrica equipos de audio. Durante el proceso de inspección se comprueba que estos equipos pueden tener 5 tipos de defectos mayores y 5 tipos defectos menores. ¿de cuántas maneras pueden ocurrir un defecto mayor y otro menor? ¿De cuántas maneras dos defectos mayores y dos defectos menores?

6. Las probabilidades de los eventos A1 y A2 son P(A1 ) = 0.40 y P(A2 ) = 0.60. También se sabe que P( A1 ∩ A2 ) = 0. Suponga que P(B/A1 ) = 0.20 y que P(B/A2 ) = 0.05. a) Son mutuamente excluyentes A1 y A2? ¿por qué sí o por qué no?
b) Calcule P(A1 ∩ B ) y P(A2 ∩ B).
c) Calcule P(B)
d) Aplique el Teorema de Bayes para calcular P( A1 / B ) y P(A2 / B ).

7. Las probabilidades de los eventos A1 , A2 y A3 son P(A1 ) = 0.20, P(A2 ) = 0.50 y P(A3 ) = 0.30. Las probabilidades condicionales de B, dados A1 , A2 y A3 son p(B/ A1 ) =0.50; que p(B/ A2 ) = 0.40 y P(B/ A3 ) = 0.30.
a) Calcule P(A1 B ), P(A2 B ) y P(A3 B ).
b) Usando el Teorema de Bayes encuentre P(A2 / B)

8. Data Consult es una empresa dedicada a la consultoría informática. Se ha presentado a un concurso para un gran proyecto de investigación. Inicialmente la dirección de la empresa pensó que tenía una oportunidad de 50% de obtener el contrato. Sin embargo, la dependencia a la que fue presentada la propuesta ha solicitado más información al respecto. Por experiencias anteriores se sabe que, cuando la dependencia solicita información adicional, la probabilidad de obtener el contrato (éxito) es el 75% de aquellas a quienes se les solicitó información adicional y sólo el 40% de las propuestas a quienes no se les solicitó información adicional, obtienen el contrato (éxito).
a) ¿Cuál es la probabilidad de tener éxito?
b) ¿Cuál es la probabilidad de tener una solicitud de informes adicionales, dado que al final la oferta será seleccionada?
c) Calcule la probabilidad de que la oferta tenga éxito, dado que se ha recibido información adicional.

9. Debido a problemas de recesión regional, una entidad bancaria ha decidido cancelar cuentas de crédito impagas. En el pasado, aproximadamente el 5% de los tarjetashabientes han dejado de pagar sin que el banco haya podido recuperar la deuda. En consecuencia, la gerencia estableció que hay una probabilidad previa de 0.05 de que un tarjetahabiente incurra en cartera vencida. Además, el banco ha visto que la probabilidad de que un cliente regular se atrase en uno o más pagos mensuales es de 0.20. Naturalmente, la probabilidad de atraso en uno o más pagos para los clientes que incurren en cartera vencida es de 1.
a) Si un cliente se atrasa en un pago mensual, calcule la probabilidad posterior de que el cliente incurra en una cartera vencida.
b) Al banco le gustaría cancelar la línea de crédito de un cliente si la probabilidad de que éste incurra en cartera vencida es mayor que 0.20. ¿debe cancelarse una línea si un cliente se atrasa en un pago mensual? ¿Por qué sí o por qué no?

10. Datos históricos indican que la probabilidad de que un hombre tenga un accidente automovilístico durante un año es dos veces la probabilidad de que una mujer lo tenga. Las probabilidades indicadas son de 0.113 para los hombres y 0.057 para las mujeres. Suponga que el 55% de los conductores en una cierta población son hombres. Al llenar una encuesta en la que se preguntaba sobre el historial de manejo, una persona de esa población indica que durante el último año tuvo un accidente automovilístico. ¿cuál es la probabilidad de que la persona sea mujer?

11. Un estudio reciente, efectuado por CPO (Consultora Peruana de Opinión) fue enfocado hacia las tecnologías usadas en el hogar. La encuesta determinó que el 60% tienen TV, el 50% tienen computadora; el 29.3% tienen una computadora y TV por cable, a la vez. De las que tienen computadora en su casa, el 64.1% dijeron que la habían usado durante la semana previa.
a) ¿Cuál es la probabilidad de que una persona tenga computadora en su casa y la haya usado la última semana?
b) ¿Cuál es la probabilidad de que una persona posea tv por cable, si se sabe que ella tiene una computadora en casa?

12. Un gerente de finanzas ha realizado dos nuevas inversiones, una en la industria petrolera y otra en bonos públicos. Dentro de un año, cada una de las inversiones se calificará como buena o mala. Considere que un experimento consiste en efectuar las dos inversiones.
a) ¿Cuántos puntos muestrales existen para este experimento?
b) Trace un diagrama de árbol y haga una lista de los puntos muestrales.
c) Sea A el evento en que la inversión petrolera es buena y B el evento en el que la inversión en bonos públicos también lo es. Haga una lista de los puntos muestrales en A y en B.
d) Haga una lista de los puntos muestrales en la unión de los eventos A y B
e) Haga una lista de los puntos muestrales en la intersección de los eventos A y B
f) ¿Son mutuamente excluyentes los eventos A y B?
13. En una encuesta de opinión realizado a visitantes de Punta Sal, se les preguntó si estaban satisfecho o no con la atención que el hotel les brinda. En la tabla siguiente se muestran las respuestas de todos los adultos y la distribución en grupos de edades.

 

	Satisfecho (%)	Insatisfecho (%)	Otros (%)
Todos los adultos	61	37	2
18 - 34	64	35	1
35 - 49	58	41	1
50 - 64	57	40	3
65 a más	70	26	4

a) ¿Cuál es la probabilidad de que un adulto seleccionado al azar esté satisfecho?
b) ¿Qué grupo de edad está más satisfecho que el promedio de todos los adultos?
c) ¿Cuál es la probabilidad de que un adulto de más de 65 años diga que no está satisfecho?

14. Se llevó a cabo una encuesta usando Call Center para determinar la respuesta del espectador a un nuevo programa de televisión, y se obtuvieron los siguientes datos:

 

Calificación	Frecuencia
Mala	4
Por debajo del promedio	8
Promedio	11
Por encima del promedio	14
Excelente	13

a) ¿Cuál es la probabilidad de que un espectador seleccionado al azar considere al nuevo programa como promedio o mejor que eso?
b) ¿Cuál es la probabilidad de que un espectador seleccionado al azar califique al nuevo programa como debajo del promedio?

15. Las cajas de ahorro municipal han observado que el monto de los ahorros han crecido durante el último año. En una muestra de 200 cuentas se obtuvieron los datos de la siguiente tabla:

 

Saldo (dólares)	Frecuencia
1000 - 1099	62
1100 - 1199	46
1200 - 1299	24
1300 - 1399	30
1400 - 1499	26
1500 a má	12

a) Si A es el evento “La deuda del cliente es menor que $1200”. Hallar P(A).
b) Si B es el evento “La deuda del cliente es más de $1300”. Determine P(B).

16. Una gran empresa de bienes al consumidor ha estado pasando un anuncio en televisión de uno de sus jabones. Llevó a cabo una encuesta y, con base en ella se asignaron probabilidades a los eventos siguientes:
S: “una persona compró el producto”
B: “una persona recuerda haber visto el anuncio”
B ∩ S : “ una persona compró el producto y recuerda haber visto el anuncio”
Las probabilidades asignadas fueron: p(B) = 0.20; p(S) = 0.40; p(BS) = 0.12.
a) ¿Cuál es la probabilidad de que una persona compre el producto, dado que recuerda haber visto el anuncio?El haber visto el anuncio, ¿aumenta la probabilidad de que una persona compre el producto? Al tomar decisiones, ¿recomendaría Ud. continuar con el anuncio, suponiendo que su costo fuera razonable?
b) Suponga que las personas que no compran el jabón de esta empresa lo compran de la competencia. ¿cuál sería su estimado de la participación del mercado para esta empresa? ¿espera Ud.que si continúa el anuncio aumente la participación del mercado para esta empresa? ¿Por qué sí o por qué no?
c) La empresa también ha probado otro anuncio y le asignó los valores P(S) = 0.30 y P(BS) = 0.10. ¿cuánto es P(B / S) para este otro anuncio? ¿cuál de los anuncios parece haber tenido el mayor efecto sobre las compras por parte de los clientes?

17. Una empresa ha realizado un análisis cuidadoso de una promoción de precios, bajo prueba en este momento. Un 20% de las personas en una gran muestra de individuos en el mercado de prueba, están enterados de la promoción y han realizado una compra. Además el 80% están enterados de la promoción, y antes de ella, 25% de las personas de la muestra compraban el producto.
a) ¿Cuál es la probabilidad de que una persona compre, dado que está enterado de la promoción?
b) Son independientes los eventos “compró” y “enterado de la promoción de precios”. ¿Porqué sí o por qué no?
c) De acuerdo con estos resultados, ¿recomendaría Ud. que la empresa introdujera esta promoción a nivel nacional? ¿Porqué sí o por qué no?

18. De un lote de 1000 productos se selecciona un producto aleatoriamente. Los defectos de fabricación se clasifican en tres tipos: A, B y C. Los defectos de tipo A ocurren el 2% de las veces; los de tipo B, el 1 % y los de tipo C, el 1.5%. Se sabe también que el 0.5% tienen los defectos de tipo A y B; el 0.6% los defectos B y C y el 0.4% presentan los defectos A y C, en tanto que sólo el 0.2% presentan los tres tipos de defectos. ¿Cuál es la probabilidad de que el dispositivo seleccionado tenga por lo menos uno de los tres tipos de defectos?

19. Por experiencias anteriores se sabe que 20 productos de un lote de producción de tamaño 100, son defectuosos. Si se selecciona una muestra aleatoria de 4 productos, ¿cuál es la probabilidad de que la muestra no contenga más de dos unidades defectuosas?

20. Una firma comercial utiliza la siguiente regla de inspección antes de almacenar los lotes de 300 artículos adquiridos: se selecciona una muestra al azar de 10 artículos. Si la muestra contiene a lo más un artículo defectuoso, se acepta el lote. De otro modo se devuelve al proveedor. Si la fracción defectuosa en el lote original es p, determinar la probabilidad de aceptar el lote como una función de p.



21. Considere el diagrama de la Figura 3.38 de un sistema electrónico que muestra las probabilidades de que los componentes del sistema operen de manera apropiada. ¿cuál es la probabilidad de que el sistema opere si el ensamble III y al menos uno de los componentes en los ensamble I y II deben operar para que funcione el ensamble completo?, si los componentes de cada ensamble operan independientemente y que la operación de cada ensamble también es independiente.

22. ¿Cómo se afecta la probabilidad del sistema si, en el problema anterior, la probabilidad para la operación exitosa del componente en el ensamble III cambia de 0.99 a 0.9?

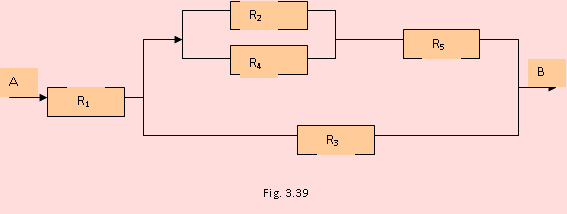
23. Considere el ensamble en serie y en paralelo que se muestra en la Figura 3.39. Los valores ri (i = 1, 2, 3, 4, 5) son las confiabilidades de los cinco componentes indicados. Esto es, Ri = probabilidad de que la i-ésima unidad funcione de manera adecuada. Los componentes operan (y fallan) de manera mutuamente independiente y el ensamble falla sólo cuando se rompe la trayectoria de A a B. Exprese la confiabilidad del ensamble como una función de R₁ , R₂ , R₃ , R₄ y R₅ .



24. Por decisión del responsable del INPE, un prisionero político será enviado a Yanahuanca o Carquín. Las probabilidades de que lo envíen a estos lugares son 0.6 y 0.4, respectivamente. Por otro lado, si se elige al azar a un residente de Puno, la probabilidad de que lleve un abrigo de piel es de 0.5, mientras que para los de Huacho dicha probabilidad es de 0.7. Al llegar al lugar de presidio la primera persona que el prisionero ve es un una persona que no lleva abrigo de piel. ¿cuál es la probabilidad de que esté en Yanahuanca?

25. Para dar solución a los problemas de patinado durante el frenado de un automóvil, que puede ser muy peligroso en los meses de lluvia, una empresa automotriz diseña un dispositivo que incluye piezas electrónicas e hidráulicas. El sistema completo puede descomponerse en tres subsistemas en serie que operan de manera independiente: un sistema electrónico, uno hidráulico y un accionador mecánico. En un frenado particular las confiabilidades de estas unidades son, aproximadamente de 0.995, 0.993 y 0.994, respectivamente. Estime la confiabilidad del sistema.

26. De una urna que contiene m bolas numeradas de 1 a m, se extraen dos bolas. Se conserva la primera bola si tiene el número 1, y se regresa en caso contrario. Cuál es la probabilidad de que la segunda bola extraída tenga el número 2?

27. Suponga que hay n personas en un cuarto. Si se elabora una lista de todos los cumpleaños (el mes específico y el día del mes), ¿cuál es la probabilidad de que dos o más personas cumplan años el mismo día? Suponga que hay 365 días en el año y que la ocurrencia de un cumpleaños sea igualmente probable para cada persona. Sea B el evento de que dos o más personas cumplen años el mismo día. Encuentre P(B) y P(B’) para n = 10, 20, 21, 22, 23, 24, 25, 30, 40, 50 y 60.

28. En cierto juego de dados, los jugadores continúan lanzando los dados hasta que ganen o pierdan. El jugador gana en el primer lanzamiento si la suma de las dos caras es 7 ú 11, y pierde si la suma es 2, 3 ó 12. De otro modo, la suma de las caras viene a ser la puntuación del jugador. El jugador continúa sus lanzamientos hasta el primer tiro bueno con el que logra su punto(en cuyo caso gana), o hasta que lanza un tiro malo (en cuyo caso pierde). ¿cuál es la probabilidad de que el jugador con los dados gane al final el juego?

29. Un grupo de consultores dirige una investigación detallada de accidentes aéreos. La probabilidad de que un accidente por falla estructural se identifique correctamente es 0.9 y la probabilidad de que un accidente que no se debe a una falla estructural se identifique en forma incorrecta como un accidente por falla estructural es 0.2. Si el 25% de los accidentes aéreos se deben a fallas estructurales, determine la probabilidad de que un accidente aéreo debido a falla estructural sea diagnosticado como falla de este tipo.

30. En la evaluación de un programa de adiestramiento en ventas, una empresa encontró que de 50 vendedores que se hicieron acreedores a un bono el año anterior, 20 habían participado en un programa especial de adiestramiento en ventas. La empresa tiene 200 vendedores. Sea B el evento en que un vendedor merece un bono y S el evento en que un vendedor participa en el programa de adiestramiento en ventas.
a) Determine P(B); p(S / B); p( S ∩ B).
b) Suponga que el 40% de los vendedores han asistido al programa de entrenamiento. ¿cuál es la probabilidad de que un vendedor alcance un bono, dado que asistió al curso de adiestramiento en ventas?

31. Una empresa estudió la cantidad de incapacidades laborales por accidente en su planta de acero en Chimbote. Los registros históricos muestran que el 6% de los empleados tuvieron incapacidades por accidente el último año. La administración cree que con un programa especial de seguridad se reducirán esos accidentes al 5% durante este año. Además estima que el 15% de los empleados que tuvieron accidentes de incapacidades durante el año pasado, volverán a tener uno durante este año.
a) ¿Qué porcentaje de los empleados tendrán incapacidades por accidente en ambos años?
b) ¿Qué porcentaje de empleados tendrán, cuando menos una incapacidad por accidente durante dos años?

32. En un estudio de hábitos de ver televisión entre casados, un investigador encontró que el 25% de los esposos y el 30% de las esposas veían con regularidad un programa popular de los sábados. El estudio indicó que en los matrimonios en que el esposo veía con regularidad el programa, el 80% de las esposas también lo veían con regularidad.
a) ¿Cuál es la probabilidad de que ambos, marido y mujer, vieran el programa con regularidad?
b) ¿Cuál es la probabilidad de que, al menos uno de ellos, marido o mujer, vea el programa con regularidad?
c) ¿En qué porcentaje de los matrimonios, al menos uno de los esposos no ve el programa con regularidad?

33. Un vendedor de sistemas empresariales vende equipo de rotulación automática de sobres, a empresas pequeñas y medianas. La probabilidad de que con un cliente nuevo se concrete una venta es de 0.10. Durante el contacto inicial con un cliente, a veces éste le pide al vendedor que lo llame después. De las 30 ventas más recientes, 12 fueron a clientes que inicialmente habían pedido al vendedor que le llamara después. De 270 clientes que no compraron, 46 habían pedido inicialmente al vendedor que los llamara después. Si un cliente pide al vendedor que lo llame después, ¿lo debe hacer? ¿cuál es la probabilidad de vender a un cliente que le ha pedido a un vendedor que lo llame después?

34. El directorio de una empresa decidió realizar una auditoría externa para que identificaran posibles declaraciones de impuestos fraudulentas. Estos auditores consideran que la probabilidad de encontrar una declaración fraudulenta, si esa declaración se acoge a deducciones por contribuciones mayores que la norma estipulada es de 0.20. Si las deducciones por contribuciones no rebasan la norma, la probabilidad de una declaración fraudulenta disminuye a 0.02. Si el 8% de todas las declaraciones rebasa la norma para deducciones por contribuciones, ¿cuál es mejor valor estimado del porcentaje de declaraciones fraudulentas?

Siguiente sesión.