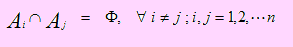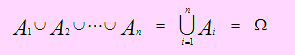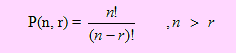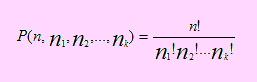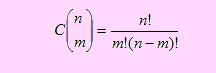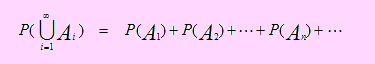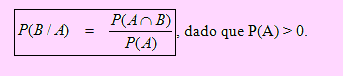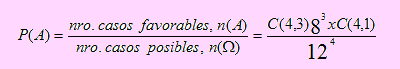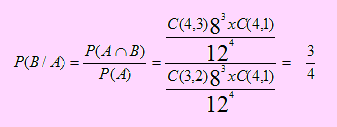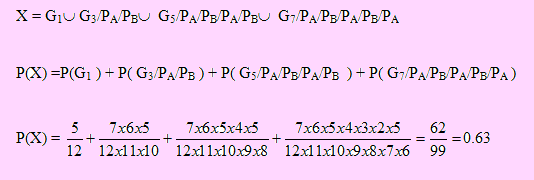TEORÍA DE LA PROPABILIDAD

3.1 Fenómenos aleatorios. Espacio muestral
3.2 Técnicas de conteo
3.3 Definición de probabilidad. Teoremas básicos
3.4 Probabilidad condicional
3.5 Probabilidad total
3.6 Teorema de Bayes
3.7 Eventos independientes
3.8 Problemas propuestos

3.1 FENÓMENOS ALEATORIOS. ESPACIO MUESTRAL

Fenómenos aleatorios

La realización o ejecución de una acción, experimento o ensayo cuyos resultados son impredecibles, constituye un fenómeno aleatorio. Usaremos ζ para denotar a un fenómeno aleatorio.

Ejemplos 01

a) Lanzar al aire una moneda una sola vez y observar el resultado.
b) Lanzar al aire una moneda tres veces y observar el resultado.
c) Registrar el color de los primeros 4 vehículos que pasan cada 10 minutos.
d) Yaco lanza un dado hasta obtener la cara con el número seis.
e) Registrar el monto total depositado en una agencia bancaria, cada hora.
f) Registrar la temperatura del ambiente cada media hora.

Espacio muestral

Es el conjunto de todos los resultados posibles obtenidos al realizar un fenómeno aleatorio. Ω será el símbolo que usaremos para denotar al espacio muestral

Ejemplo 02

El espacio muestral asociado a los fenómenos aleatorios del ejemplo anterior son:
Ω₁ = {C, S}
Ω₂ = {SSS, SSC, SCS, CSS, SCC, CSC, CCS, CCC}
Ω₃ = {(rojo, verde, negro, blanco), (rojo, negro, blanco, azul),…}
Ω₄ = {6, x6, xx6, xxx6, xxxx6, xxxxx6,… donde x representa la cara 1, 2, 3, 4 ó 5}
Ω₅ = {1200.35, 34564.17, 0, 17.18, 272634.0,…}
Ω₆ = {22ºC, 22.2ºC, 23.17ºC, 22.8ºC,…}

Eventos

Sea ζ un experimento aleatorio y Ω, el espacio muestral asociado a ε ; diremos que A es un evento de Ω si A ε Ω.



Ejemplo 03

Al lanzar una moneda tres veces, definimos el evento A como "Sale cara por lo menos dos veces".

En este caso definimos al experimento ζ como “Lanzar al aire tres monedas”, para el cual, Ω = {(S, S, S), (S, S, C), (S, C, S), (C, S, S) (S, C, C), (C, S, C), (C, C, S), (C, C, C) }
De acuerdo a la definición, A = {(S, C, C), (C, S, C), (C, C, S), (C, C, C)}

Ejemplo 04

Fuji, Vladi y Couri, cada uno desde su trinchera, deben recibir un premio por su destacada labor de "convencimiento" a los congresistas. El amauta Kenyi sólo otorgará dos premios, diferentes entre sí. El experimento consiste en seleccionar a dos de ellos para entregarles los premios.
a) Defina el espacio muestral, mostrando todos sus elementos.
b) Si el evento A se define como: "El primer premio lo gana Fuji”; el evento B se define como “Los dos premios lo ganan Vladi y Couri”. Describa A y B.

Solución

a) Puesto que Fuji, Vladi y Couri, deben competir por los dos premios,  ={(Fuji,Vladi),(Fuji, Couri),(Vladi, Fuji),(Vladi, Couri), (Couri, Fuji),(Couri, Vladi)}.

b) El evento A está formado por pares ordenados en donde la primera componente es Fuji; es decir, A = {(Fuji,Vladi),(Fuji, Couri)} En el caso del evento B tenemos B = {(Vladi, Couri), (Couri, Vladi)}

Evento imposible

El conjunto vacío φ constituye un evento imposible. Es un evento que nunca ocurre.

Evento cierto

El espacio muestral Ω recibe el nombre de evento cierto. Siempre ocurre.

Nota:

Los eventos Ω y φ son eventos contrarios. φ nunca ocurre, mientras que Ω siempre ocurre.

Eventos mutuamente excluyentes

Diremos que dos eventos definidos sobre el mismo espacio muestral son mutuamente excluyentes si no ocurren simultáneamente; es decir, si no ocurren juntos.

Sean A y B dos eventos de Ω. Diremos que A y B son eventos mutuamente excluyentes si A ∩ B = φ.

Complemento de un Evento

Diremos que A’ es el complemento del evento A siempre que en A’ no estén ninguna ocurrencia de A; es decir, A’ = Ω - A.

Nota:

Los eventos A y A’ son eventos complementarios. Los eventos Ω y φ son también eventos complementarios.

Ejemplo 05

Sean A y B eventos de Ω. Si A y B son mutuamente excluyentes
a) Exprese los eventos A y B como la unión de dos eventos mutuamente excluyentes
b) Exprese los eventos A’ y B’ como la unión de dos eventos mutuamente excluyentes.

Solución



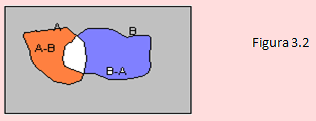
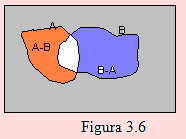
En el diagrama anterior distinguiremos tres niveles de grises: Gris 1, lo que corresponde a una parte de B; Gris 2, lo que corresponde a una parte de A y Gris 3, lo que está fuera de A y B.

Por definición

A - B = A ∩ B’
B - A = A ∩ B

Al evento A’ le corresponde el Gris 2
Al evento B’ le corresponde el Gris 1
Al evento A’B’ le corresponde el Gris 3
Al evento AB le corresponde la parte blanca

Según esto,

a) A = A ∩ B ∪ A ∩ B’         B = A ∩ B ∪ A’ ∩ B
b) Juntando la parte gris y azul, tenemos A’; es decir, A’ = A’B’ ∪ A’B Del mismo modo, gris y naranja es B’; es decir, B’ = A’B’ ∪ AB’.

Eventos mutuamente excluyentes para más de dos conjuntos

Una colección de eventos A1, A2,..., An, definidos sobre un mismo espacio muestral Ω, constituyen Eventos Mutuamente Excluyentes, si la ocurrencia de uno de ellos, excluye la ocurrencia de los otros; es decir,



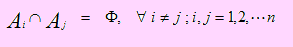
Eventos colectivamente exhaustivos

Se dice que una colección de eventos A1, A2,..., An , definidos sobre un mismo espacio muestral  son Colectivamente Exhaustivos, si la unión de todos ellos es el espacio muestral; es decir,



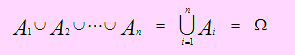
Ejemplo 06

Un portafolio de acciones contiene cuatro acciones comunes. Durante un determinado día de negociación, se define los siguientes eventos:
A: “Más de la mitad de las acciones subirán de precio”
B: “Más de la mitad de las acciones bajarán de precio”
C: “Más de la mitad de las acciones no cambiarán de precio”

a) Exprese en palabras la ocurrencia de los siguientes eventos: A ∪ C y A ∩ B
b) ¿Son los eventos A y B mutuamente excluyentes? ¿Y A y C? ¿Y B y C?
c) ¿Son los eventos A, B y C colectivamente exhaustivos?

Solución

a) El evento compuesto AB representa: “Más de la mitad de las acciones subirán o bajarán de precio”.
El evento compuesto AB representa: “Más de la mitad de las acciones subirán y bajarán de precio”, esto no ocurre, por lo que AB es un evento imposible.

b) Los eventos A y B sí son excluyentes porque cuando se pacta para una negociación, esta se realiza con los precios en alza o en baja, pero no tiene sentido en ambos.
Los eventos A y C también son mutuamente excluyentes por el mismo razonamiento.
Del mismo modo los eventos B y C se excluyen mutuamente ya que nadie (en su sano juicio) paga el mismo precio si las acciones están de baja o se mantienen constantes.
c) No son exhaustivos ya que “más de la mitad” significa más del 50%; esto implica que si ocurre “más de la mitad” suben de precio, “menos de la mitad” podrían bajar de precio.

3.2 TÉCNICAS DE CONTEO

Principio de adición

Supongamos que los elementos de A se pueden agrupar de m maneras y del mismo modo los elementos de B se pueden agrupar de n maneras. El número de maneras de agrupar los elementos de A ó de B, sin que se repitan, es m + n;en otras palabras, podemos formar otro conjunto, digamos C, que constituye la unión de A y B. En este caso, n(C) = n(A) + n(B).

En efecto, si A = {1, 3, 5, 7, 9} y B = {2, 4, 6, 8}, entonces n(C) = n(A  B)= 9; es decir, el número de elementos que pertenezcan a los eventos A óB; es 9.

Principio de multiplicación

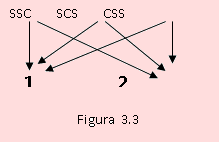
Supongamos ahora que se dispone de un mecanismo el cual se puede manifestar de m maneras; y otro mecanismo puede también manifestarse de n maneras; el número de maneras de manifestarse el primero y el segundo, es el producto, m x n. En efecto, si el número de maneras de obtener una cara, al lanzar al aire tres monedas, es 3, y si el número de caras menores a 3, que se puede obtener al lanzar un dado, es 2, entonces, el número de maneras de obtener una cara con la moneda y un número menor a 3 con el dado, es 6; es decir,  = {(SSC; 1), (SCS; 1), (CSS; 1), (SSC; 2), (SCS; 2),(CSS; 2)} Esquemáticamente



Permutación

Si de un conjunto de n elementos, deseamos obtener grupos de tamaño r cada uno, en los que interesa la ubicación de los elementos, el número de maneras de hacerlo se define como "permutaciones de n elementos tomados de r en r", el cual se denota por P(n,r) y se define como



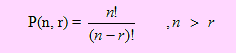
Del mismo modo, si se considera la repetición de sus elementos, se tiene permutación con repetición, definido por:

Pr(n,r) = n^r

Permutaciones cuando no todos los elementos son diferentes
. Si de un conjunto de n elementos, se desea formar grupos que contengan n₁ elementos de una clase, n₂ de una segunda clase,…, n_k elementos de una k-ésima clase, con n = n1 + n2+…. + nk, entonces el número de permutaciones de esos elementos está dado por



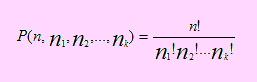
Ejemplo 07

Cuántos cifras de tres dígitos se pueden formar con los dígitos decimales,
a) si no se deben repetir los dígitos y no se considera el 0?
b) Si no se deben repetir los dígitos y se considera el 0?
c) Si se repiten los dígitos y se considera el 0?

Solución

Ante todo, el número de dígitos decimales es 10; es decir, n = 10. Como se desea formar número de tres dígitos, entonces m = 3. Por otro lado, en cada grupo de tres dígitos nos interesa tomar en cuenta la ubicación de los mismos; el "grupo" 267 es diferente al 672; diferente al 762, etc. Esta es la razón por la cual debemos usar permutaciones: nos interesa el orden de ubicación de los elementos.

a) Si no se considera el 0, disponemos de 9 dígitos, n = 9. Como ninguno de los nueve debe repetirse, P(9, 3) es la cantidad de números que podemos formar; es decir, P(9, 3) = 9! / (9 - 3)! = 9x8x7 = 504

b) Aquí, debemos tomar en cuenta n = 10, con lo que se tiene P(10, 3). Pero de esta cantidad debemos eliminar los casos en los cuales el dígito cero ocupa la primera posición. Según esto, la posición de las centenas puede ser ocupada solamente por los 9 dígitos (estamos eliminando el cero); esto no da P(9, 1) maneras. La posición de las decenas y de las unidades puede ser ocupada por cualquiera de los 9 dígitos restantes (donde sí se considera el cero); por lo que, el número de cifras de 2 dígitos será P(9, 2). Ahora, como debemos formar números tomando en cuenta la cantidad de maneras de obtener las centenas y la cantidad de maneras de obtener las decenas y unidades, usando el principio de la multiplicación, tendremos que
El número de cifras es P(9, 1)xP(9, 2) = 648.

c) Ahora sí debemos considerar permutaciones con repetición, por cuanto se permite la repetición de cualquiera de los diez dígitos en las posiciones de las decenas y unidades y sólo 9 de ellos en la posición de las centenas. Esto indica que el número de maneras será
P(9, 1)xPr(10,2) = 9 x 102 = 900

Ejemplo 08

De cuántas maneras diferentes se pueden sentar tres damas y tres varones en una banca,
a) ¿Si no interesa la ubicación de entre ellos?
b) ¿Si tanto las damas como los varones deben estar juntos?
c) ¿Si sólo los varones deben estar juntos?
d) ¿Si los varones ocupan los lugares impares?

Solución

A diferencia del respecto al ejemplo anterior, aquí las personas no pueden repetirse, pero sí interesa quién está junto a quién; por ello interesa el orden, por lo que usaremos permutación.

a) Como no interesa la ubicación entre ellos, simplemente tenemos 6 elementos para formar grupos de 6 en 6. Por ello, el número de maneras será P(6, 6 ) = 6! = 720.

b) Si las damas deben estar juntos, debemos contemplar de cuántas maneras pueden sentarse juntas; esto es P(3, 3).
Del mismo modo, P(3, 3) es la cantidad de maneras en que los varones se sentarán juntos. Usando el principio de la multiplicación, P(3, 3)xP(3, 3) es el total de maneras. Algo más: las damas pueden sentarse a la izquierda o a la derecha. Esto genera dos maneras diferentes de formar cada uno de los P(3, 3)xP(3, 3) grupos. Luego, el total de maneras de sentarse será 2 x P(3, 3)xP(3, 3) = 2 x 6 x 6 = 72.

c) Aquí sólo los varones deben estar juntos. El esquema siguiente refleja la situación.



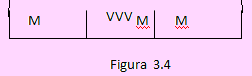
El total de maneras de ubicarse los varones es P(3, 3). Tomémoslo como si fueran una unidad. Esta unidad puede insertarse antes, después y entre las tres damas. Esto implica que pueden ubicarse en 4 lugares diferentes. Como las damas se pueden ubicar de P(3, 3) maneras, el total de maneras pedido será 4 x P(3, 3) x P(3, 3) = 144

d) Si los varones deben ocupar los lugares impares, entonces deben sentarse en los lugares 1, 3 y 5. Y el número de manera de ubicarlos ahora es P(3,3). Ahora bien, las damas ocuparán los lugares pares de P(3, 3) maneras.

El número de maneras de ubicar a los varones en los lugares impares y a las damas en los lugares impares es, P(3, 3) x P(3, 3) = 36.

Combinaciones

Si de un conjunto de n elementos, deseamos obtener grupos de tamaño m cada uno, donde no interesa el orden de ubicación o selección de los elementos, el número de maneras de hacerlo se define como "combinaciones n elementos tomados de m en m", el cual se denota por C(n, m) y se define como



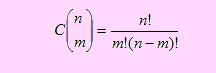
Ejemplo 09

Una firma comercial tiene 10 vendedores. ¿De cuántas maneras puede asignarse los vendedores en dos escritorios con
a) Cinco vendedores en cada escritorio?
b) Siete vendedores en un escritorio y 3 en el otro?
c) Si ahora se dispone de 3 escritorios, de cuántas maneras se puede asignar 3 vendedores al primero, 3 al segundo y 4 al tercer escritorio?

Solución

a) Puesto que cualquier vendedor puede sentarse en cualquiera de los 5 escritorios, el número de maneras de asignarse escritorios a los 5 primeros será C(10, 5). El otro escritorio puede ser asignado a los restantes 5 vendedores de C(5, 5) maneras. Luego, el número de maneras de asignar los dos escritorios a los 10 vendedores es
C(10, 5)x C(5, 5); es decir

C(10, 5) x C(5, 5) = (10x9x8x7x6 ) / (5x4x3x2) x 1 = 252.

b) En este caso C(10, 7) es el número de maneras de asignar el primer escritorio a 7 de los vendedores. Los restantes 3 se ubican en el segundo escritorio, de una sola manera. Luego C(10, 7) = 120 es el total de maneras de lograr lo pedido.

c) Siguiendo el mismo razonamiento: Tres vendedores son asignados de C(10, 3) maneras. Los siguientes 3 se asignan de C(7, 3) maneras y los restantes 4 se asignan de C(4, 4) maneras en el tercer escritorio. Esto es, de C(10, 3) x C(7, 3) x C(4, 4) = 120 x 35 x 1 = 4200 maneras.

Ejemplo 10

Un testigo de un accidente automovilístico informa a la policía que la placa del automóvil que originó el accidente era amarilla y comenzaba con la letra A y terminaba en 5. ¿Cuántos automóviles deberá investigar la policía de la ciudad de Lima a fin de ubicar al vehículo en cuestión?

Solución

Como sabemos, en Lima todas las placas amarillas están formadas de 3 letras y 3 dígitos.

 

A

5

Siendo la primera letra A, la segunda y tercera letras pueden ser escogidas de Pr(26, 2) maneras; es decir, de 26² maneras.
Del mismo modo, los dos dígitos que faltan pueden ser elegidos de Pr(10, 3) = 1000 maneras.
Luego el número de placas que debe investigar la policía es 26²x1000 = 676000.

3.2 DEFINICIONES DE PROBABILIDAD. TEOREMAS BÁSICOS

La Teoría de la Probabilidad nos dirá que para medir la ocurrencia de un evento existen tres formas equivalentes:

a) Mediante el concepto de frecuencia relativa
b) Mediante el concepto de probabilidad clásica
c) Mediante la forma axiomática
Antes de continuar veamos el siguiente experimento realizado en Excel: Este ejemplo consiste de dos experimentos realizados por el autor: a) Lanzar una moneda 100 veces y observar el número de veces que sale cara.
b) En MS EXCEL, realizar simulaciones de lanzamiento de una moneda mediante el uso de números aleatorios, y observar los resultados.

Resultados

a) En este caso, luego de lanzar al aire una moneda de S/. 5.00 obtuve los siguientes resultados:
Número de caras     48
Número de sellos     52
Según lo dicho anteriormente,
f = Casos favorables 48
n = Casos posibles 100
Si dividimos f entre n obtenemos 0.48. Esto significa que en el 48% de las veces obtuve cara.

b) La siguiente imagen muestra los resultados de la simulación, usando Excel. Debemos indicar que estos resultados se ha obtenido sin haber fijado los números aleatorios que se generaron inicialmente y habiéndolos dejado “flotar”, y estando activado el re cálculo automático. En esta figura se muestra la frecuencia del número de caras obtenidas.



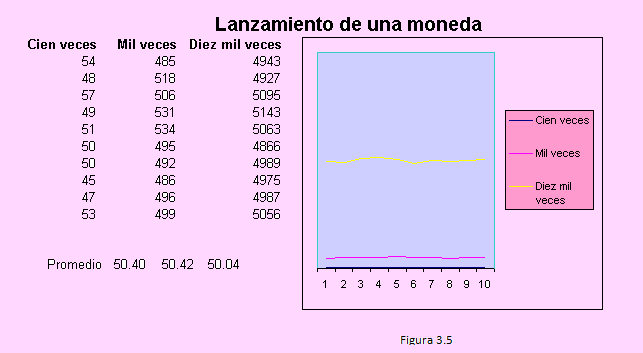
Observando la gráfica para las tres situaciones vemos sorprendentemente que la frecuencia, porcentaje o proporción de caras tiende a ser constante; y analizando los datos numéricos, encontramos que, muy cerca de la mitad del número de lanzamientos corresponde a las veces que ha salido cara y la otra mitad a sello.

En efecto, en promedio, luego de las diez simulaciones, casi exactamente el 50% de las veces ha ocurrido cara y 50% de las veces ha ocurrido sello. Esto me autoriza a decir que si lanzo al aire una moneda, una sola vez, la confianza que tengo de que salga cara es de 50%, es decir de 1/2?

Y si ahora lanzo un dado, tendré la confianza del 16.6667%, es decir de 0.16667 de que la cara superior obtenida sea 4? ¿Y que la confianza aumenta a 1/2 si la cara mostrada es par? Finalmente, ¿querrá esto decir que, sujeto a resultados previos en otros experimentos; es decir, sujeto a resultados y datos históricos de otros ensayos o experimentos, puedo planificar acciones futuras con la certeza que me proporcione esta forma de medir resultados favorables respecto a resultados posibles en la realización de un experimento? .... Interesante ¿no?.

En ambos ejemplos y de lo verificado con los experimentos, debemos ser capaces de cuantificar la relación que existe entre los resultados favorables y los resultados posibles. ¿Podríamos usar el concepto de proporción de resultados que favorecen la ocurrencia de un evento, que como hemos visto nos ofrece conclusiones muy interesantes? Sea como proporción, como porcentaje o como fracción, ¿no estaremos "midiendo" la ocurrencia de un evento en particular, es decir la medida de un resultado favorable respecto a los resultados posibles?

En efecto, la Teoría de Probabilidades nos dirá que la forma de medir la ocurrencia de un determinado evento, digamos A, dentro de un espacio muestral , el cual está asociado a un experimento , constituye la Probabilidad de la ocurrencia de dicho evento, lo cual se denotará por P(A)

Definición de probabilidad como una frecuencia relativa

Supongamos que el experimento ζ se repite un número de veces muy grande. Sea Ω el espacio muestral asociado a ζ,, donde n(Ω) = n. Supongamos que el evento A ocurre un número determinado de veces, digamos n_A , es decir, n(A) = n_A .

Diremos que P(A) representa la probabilidad de la ocurrencia del evento A, la que se define como la frecuencia relativa del número de ocurrencias del evento respecto al número de veces que se ha realizado el experimento; es decir, P(A) = n_A / n


Definición clásica de probabilidad

Supongamos que el experimento ζ se repite un número determinado de veces. Sea Ω el espacio muestral asociado a ζ, donde n(Ω) = n. Supongamos que el evento A ocurre un número de veces, digamos n_A , es decir, n(A) = n_A . Diremos que P(A) representa la probabilidad de la ocurrencia del evento A y se define como la razón entre el número de casos favorables a la ocurrencia de A, sobre el número de casos posibles; esto es, P(A) = n(A) / n(Ω) = n_A / n

Definición axiomática de probabilidad

Sea ζ un experimento y Ω el espacio muestral asociado a ζ. Sea A un evento de Ω, de tal manera que A está contenido en Ω. A cada evento A, le asociamos una función real, denotado por P(A) siempre que se satisfaga las siguientes propiedades:

i) 0 ≤ P(A) ≤ 1

ii) P(Ω) = 1

iii) Si A y B son eventos mutuamente excluyentes, entonces P(A ∪ B) = P(A) + P(B)

iv) Si A₁ , A₂ , A₃ … A_n … son eventos que se excluyen mutuamente, dos a dos, entonces



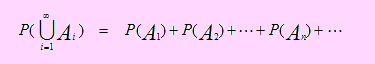
Probabilidad del evento complementario

Si A’ es el evento complementario de A, entonces P(A’) = 1 – P(A).

Probabilidad de la unión de dos eventos cualesquiera

Si A y B son dos eventos cualquiera de Ω, entonces P(A ∪ B) = P(A) + P(B) – P(A ∩ B).



En el caso de tres eventos:

Si A, B y C son tres eventos cualquiera de Ω entonces,

P(A ∪ B ∪ C) = P(A) + P(B) + P(C) - P( A ∩B) - P( A ∩ C) - P( B ∩ C) + P( A ∩ B ∩ C)

Ejemplo 11

El neumático del auto de un alumno tiene un clavo y el 20% del neumático es visible. Si el automovilista se detiene, ¿cuál es la probabilidad de que el clavo quede en la parte visible?

Solución



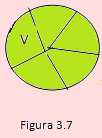
En la figura anterior, cada sector representa la quinta parte del círculo. Si suponemos que el sector V es el sector visible y definimos al evento A: “El sector V es visible”, entonces P(A) = 1/5 = 0.20

Ejemplo 12

Sea P(A)=0.4, P(B)=0.5, P(C)=0.7, P(AB) = 0.2, P(AC)=0.2, P(BC) = 0.2 y P(ABC)=0.1.

Evalúe las siguientes probabilidades.

a) P(A ∪ B ∪ C)
b) P(A ∪ B ∪ C’)
c) P(A ∪ B)
d) P(A’ ∪ B’ )
e) P(A’C’)
f) P(A’B’C’)



Solución

a) Por propiedades sabemos que

P(A ∪ B ∪, C) = P(A) + P(B) + P(C) – P(AB) – P(AC) – P(BC) + P(ABC)
= 0.4 + 0.5 + 0.7 – 0.2 – 0.2 – 0.2 + 0.1 = 0.11

b) P(A ∪, B ∪ C’) = P(A) + P(B) + P(C’) – P(AB) – P(AC’ ) – P(BC’ ) + P(ABC’ )
Como P(C’) = 1 – P(C)

Si P(A)=0.4, P(AC’ ) = P(A) – P(parte naranja) – P(parte roja) = 0.4 – 0.1 –0.1 =0.2

Si P(B)=0.5, P(BC’) = P(B) – P(parte roja) – P(parte verde) = 0.3

P(ABC’) = P(parte azul) = P(AB) – P(ABC) = 0.1

Luego P(A ∪ B ∪ C’) = 0.4 + 0.5 + (1-0.7) – 0.2 – 0.3 + 0.1 = 0.8

c) P(A  B) = P(A) + P(B) – P(AB) = 0.4 + 0.5 – 0.2 = 0.7

d) P(A’  B’ ) = P[(AB)’] = 1 – P(AB) = 1 – 0.7 = 0.3.

e) P(A’ C ’) = P[(A  C)’] = 1 – P(A  C) = 1 – ( 0.4 + 0.7 – 0.2) = 0.1

f) Como A’B’C’ = (A  B  C)’, y de a) tenemos P(A  B  C) = 0.11, entonces

P(A’B’C’) = P(A  B  C)’ = 1 - P(A  B  C) = 1 – 0.11 = 0.89.

Ejemplo 13

¿Cuál o cuáles de los siguientes incisos representan eventos que son:
(1) colectivamente exhaustivos,
(2) mutuamente excluyentes dos a dos?

a) P(A) = 0.6, P(B) = 0.2, P(C) = 0.1, P(AB) = 0.0
b) P(A) = 0.1, P(B) = 0.4, P(C) = 0.5, P(A  B ) = P(C), P(A  C) = 0.6 y P(BC) = 0
c) P(A) = P(B) = 0.2, P(C) = 0.6, P(AB) = 0, P(A  C)= P(B  C) = 0.8
d) P(A) = P(B) = P(C) = 0.35, P(AB) = P(AC) = 0.

Solución

Ante todo, recordemos que:
i) A, B, C son eventos colectivamente exhaustivos si A ∪ B ∪ C = Ω.
ii) Dos eventos son mutuamente excluyentes si no ocurren ambos a la vez.
iii) En este caso, como A  B  C = , entonces se cumple que P(A ∪, B ∪ C)=1.

Veamos:

a) P(A ∪ B ∪ C) = P(A) + P(B) + P(C) – P(AB) – P(AC) – P(BC) + P(ABC).
Como P(AB) = 0, entonces AB = φ, con lo cual, P(ABC) = 0.
Si por otro lado, P(A) + P(B) + P(C) = 0.9, al restarle los otros términos seguirá siendo menor que uno, con lo cual diremos que A, B y C no son colectivamente exhaustivos.
Del mismo modo, no son mutuamente excluyentes dos a dos, a pesar de P(AB) = 0, ya que si así fuera, P(A ∪ B ∪ C) sería uno, lo que no es cierto.

b) Si P(BC) = 0, entonces P(ABC) = 0 ya que ABC = φ. Como 0.5=P(C )=P(AB)=P(A) + P(B) - P(AB) = 0.1 + 0.4 – P(AB) con lo cual P(AB)=0.

Del mismo modo, si P(A ∪ C) = 0.6, podemos concluir que P(AC) = 0 (¿?). Por tanto, A, B y C son colectivamente exhaustivos ya que P(A ∪ B ∪ C ) = 1.0

Son también mutuamente excluyentes ya que P(AB) = P(AC) = P(BC) = 0

c) Como en el caso anterior, si P(AB) = 0, entonces P(ABC) = 0; con lo cual diremos que los eventos son mutuamente excluyentes dos a dos. Por otro lado, y siguiendo el mismo razonamiento del caso anterior, los tres eventos A, B y C son colectivamente exhaustivos.

d) Con los datos de la pregunta,
P(A ∪ B ∪ C) = P(A) + P(B) + P(C) – P(AB) – P(AC) – P(BC) + P(ABC)
= 0.35 + 0.35 + 0.35 - 0 - 0 - P(BC) + 0

Como P(A ∪ B ∪ C) no puede ser mayor que uno, P(BC) debe ser 0.05.

Esto indica que
- los tres eventos no son colectivamente exhaustivos
- los pares de eventos A, B y A, C son mutuamente excluyentes, pero B y C no lo son.

Ejercicio 01

Sean X, Y y Z eventos de Ω. Supongamos que P(X) = 0.7, P(Y) = 0.5, P(XY’) = 0.3 y P(XY’Z’) = 0.1. Evalúe

a) P([X ∪ (X’Y)]’)                 c) P(X’ ∪ Y’Z)
b) P(XY ∪ [X ∪ X’Y’ ]         d) P(X’Y ∪ XY’ )(exactamente ocurre uno)

Ejercicio 02

Si P(X) = 0.5, y P(X ∪ (Y’Z’ )’ ) = 0.8, determinar P(X’ (Y ∪Z))

Ejercicio 03

Sean X, Y, Z eventos de &Omega. Exprese en términos de P(X), P(Y), P(Z), P(XY), P(XZ) y P(XYZ), para k = 0, 1, 2, 3 la probabilidad de que

a) ocurran exactamente k de los eventos X, Y, Z
b) ocurran por lo menos k de los eventos X, Y, Z
c) ocurran cuando menos k de los eventos X, Y, Z

Ejemplo 14

Yaco se presenta a dos universidades A y B. Su padre estima la probabilidad de que logre ingresar a la Universidad A en 0.8; a la Universidad B, en 0.75; en, al menos una de ellas, en 0.95. ¿Cuál es la probabilidad de que ingrese a ambas universidades?

Solución.

Según los datos, P(A) = 0.8, P(B) = 0.75, P(A ∪ B ) = 0.95. Debemos hallar P(AB).

De 0.95 = P(A  B) = P(A) + P(B) – P(AB) = 0.8 + 0.75 – P(AB), obtenemos P(AB) = 0.6
Y como AB es el evento “ingresar a ambas universidades”, la probabilidad pedida será 0.6

Sugerencia: Represente los eventos usando Diagramas de Venn para visualizar el problema.

Ejemplo 15

De una urna que contiene dos bolas rojas, una azul y tres verdes, se extraen aleatoriamente dos de ellas. Calcule la probabilidad de que las dos bolas sean verdes o una roja y otra azul.

Solución

Sea A: “las dos bolas extraídas son verdes”
B: “la primera bola es roja y la segunda azul”
Debemos encontrar P(A  B ).

Aunque el problema no lo dice, supondremos que la primera bola extraída no es devuelta a la urna. Es decir, se realiza experimentos sin reposición por lo que los casos posibles y favorables se obtiene usando combinaciones. Es equivalente si se extrae las dos bolas a la vez

Lugo el número de maneras de extraer dos bolas de un total de 6, es C(6, 2)
Dos verdes se obtiene de C(3, 2) maneras. Luego P(A) = C(3, 2) / C(6,2) = 3/15

Otra forma de obtener P(A): La probabilidad de obtener una verde en la primera extracción es 3/6. La probabilidad de obtener verde en la segunda, sabiendo que ya salió en la primera, es 2/5 (ya que sólo quedan 5 de las cuales dos son verdes).

Luego la probabilidad de que salgan verde la primera y verde la segunda, es (3/6)(2/5) = 3/15.

Por otro lado, usando cualquiera de las formas, P(B) = (2/6)(1/5) = 1/15

Por tanto, P(A &∪ B) = P(A) + P(B) = 3/15 + 1/15 = 4/15. (A y B son mutuamente excluyentes)

Ejemplo 16

Un conjunto de alumnos tienen acceso a tres páginas de Internet: Web1, Web2 y Web3. Una encuestadora de opinión realizó una consulta y obtuvo los siguientes resultados. El 20% de los alumnos acceden a la página Web1, 30% acceden a Web2 y 25% acceden a Web3; 10% acceden a Web1 y Web2; 8% acceden a Web1 y Web3; 12% acceden a Web2 y Web3; 3% acceden a las tres páginas. Si se selecciona a un alumno, ¿cuál es la probabilidad de que acceda a una de las tres páginas?

Solución

El siguiente diagrama adjunto muestra la probabilidad de ocurrencia de cada uno de los sectores del mismo.
Tomando en cuenta el diagrama anterior, definamos los siguientes eventos:



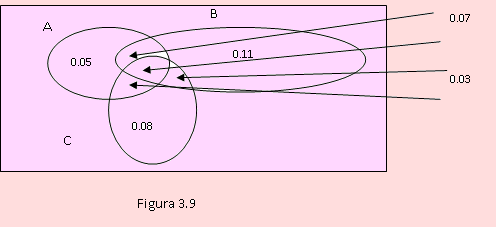
A: “Acceden a la página Web1”
B: “Acceden a la página Web2”
C: “Acceden a la página Web3”
Sean W el evento: “Accede por lo menos a una página”.

Según esto, “accede por lo menos a una página” está representado por A ∪ B ∪ C.
Luego P(W) = P(A ∪ B ∪ C) = P(A) + P(B) + P(C) – P(AB) – P(AC) – P(AC) + P(ABC)
      = 0.20 + 0.30 + 0.25 – 0.10 – 0.08 – 0.12 + 0.03
     = 0.48

Otra forma:

“Acceder a por lo menos a una página” es el complemento del evento W’: “Acceder a cero páginas”. Esto implica que P(W) = 1 - P(W’ ) = 1 - P(A’ B’ C’ ) = 1 - 0.52 (en la figura, todo lo que no está en A, B y C).

Ejercicio 04

Un agente vendedor intenta colocar un determinado producto a tres de sus probables clientes A, B y C. La probabilidad de que el cliente A o B, pero no C compren el producto, es 0.65, la probabilidad de que el primero y el segundo compren, es 0.20. La probabilidad de que haga la primera venta pero no la tercera es 0.25. La probabilidad de que ni el primero ni el segundo compren, es 0.25; la probabilidad de que no compre el segundo pero sí el tercero, es 0.30. ¿Cuál es la probabilidad de que sólo uno de los dos primeros, pero no el tercero, compren?

3.4 PROBABILIDAD CONDICIONAL

Sea  el espacio muestral asociado al experimento  . Sea A y B dos eventos de . Supongamos que el evento A, ya ha ocurrido con P(A) > 0. Según esto, diremos que P(B/A) representa la “probabilidad condicional de que ocurra el evento B, sabiendo que ha ocurrido el evento A”, el cual se define como



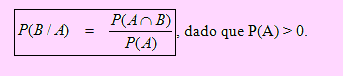
Esquemáticamente, supongamos que la probabilidad de que el evento A ocurre, es de 0.40. Si ocurre A, la probabilidad de que ocurra B, es 0.20; si no ocurre A, la probabilidad de que B ocurra es 0.30. En el diagrama siguiente, conocido como Diagrama de árbol, se muestra estas probabilidades. Observe que en la primera “etapa” hablamos de la ocurrencia o no del evento A; en la segunda “etapa”, estamos interesados en averiguar la ocurrencia o no, de B.



Según los datos:

P(A) = 0.40
P(A’) = 0.60
P(B/A) = 0..20
P(B’/A) = 0.80
P(B/A’) = 0.30
P(B’/A’) = 0.70

Teorema de la multiplicación

De la definición de probabilidad condicional, podemos extraer las siguientes ecuaciones:

P(A ∪ B) = P(A) P(B / A)

Del mismo modo, P(A ∪ B) = P(B) P(A / B)

A estas dos ecuaciones se les conoce como el teorema de la multiplicación o probabilidad de la intersección. Es decir, la probabilidad de que ocurran los dos eventos simultáneamente, sabiendo que uno de ellos ya ocurrió, es el producto de la probabilidad de la ocurrencia del segundo sabiendo que ha ocurrido el primero, por la probabilidad de la ocurrencia del primero.

En general:

Sean A₁, A₂ ,... A_n , eventos del espacio muestral Ω. Si suponemos que todas las probabilidades existen, entonces

P(A₁ ∪ A ₂ ∪ ... ∪ A_n) = P(A₁)P(A₂/A₁) ... P(A_n / A₁ ∪ A₂ ∪ ... ∪ A_n-1)

Ejemplo 17

Si P(A) = 1/2, P(B) = 1/3 y P(AB) = 1/4 , evaluar P(A ∪ B), P(A/B), P(B/A) y P(A ∪ B/B).

Solución

P(A ∪ B) = P(A) + P(B) – P(A ∩ B) = 1/2 + 1/3 - 1/4 = 7/12

P(A / B ) = P(A ∩ B) / P(B) = 0.25 / 0.3333 = 0.75

P(B / A ) = P( A ∩ B) / P(A) = 0.25 / 0.5 = 0.5

Evaluemos P(A ∪ B / B )

Si (A ∪ B) ∩ B = B, entonces P( A ∪ B / B) = P(B) / P(B) = 1

Ejemplo 18

Dos radios defectuosos son mezclados con otros dos buenos.
Se prueban los radios, de uno en uno hasta encontrar los dos defectuosos. ¿Cuál es la probabilidad de que el
a) último radio defectuoso sea encontrado en la segunda prueba?
b) el último radio defectuoso sea encontrado en la tercera prueba?

Solución

Sea A: “El último radio defectuoso es encontrado en la segunda prueba”
B: “El último radio defectuoso es encontrado en la tercera prueba”

En el diagrama de la figura 3.11,

a) El segundo defectuoso sale en la segunda prueba con P(A) = P(D₂/D₁) P(D₁ )= 1/6



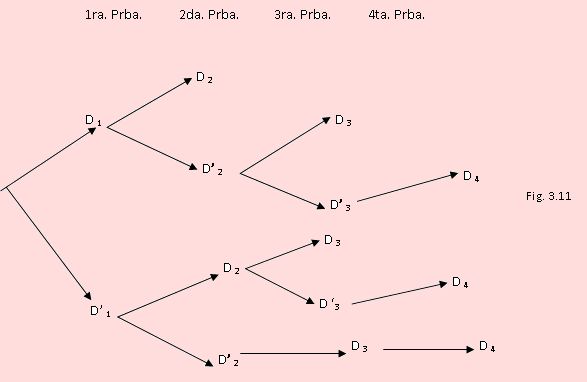
b) El Segundo defectuoso sale en la tercera prueba de dos maneras: Que en la segunda salga D₂’ habiendo salido D₁ en la primera:
Que en la segunda salga D₂ habiendo salido D₁’ en la primera

Esto es P(B) = P(D₃ / D₂ ‘ )P(D₂‘ / D₁) P(D₂ ) + P(D₃ / D₂ )P(D₂ / D₁ ‘)P(D₁ ‘)
                    = 1/2 x 2/3 x2/4 + 1/2 x 2/3 x2/4     =     1/3

Ejemplo 19

Piero Petroni tiene dos vehículos para trasladarse a su centro de trabajo. Como consecuencia de haberlo sometido a grandes jornadas de trabajo, los dos vehículos tienen problemas en el momento del arranque inicial.

La probabilidad de que uno u otro arranquen es 0.1; la probabilidad de que arranque el segundo, pero no el primero, es 0.2; la probabilidad de que ninguno de ellos arranquen es 0.4. Hallar la probabilidad de que
El primer vehículo arranque
Arranque el primero, sabiendo que el segundo arrancó.
[ Arranque el segundo, si el primero no arrancó

Solución

Sean los eventos
A: “El primer vehículo arrancó”
B: “El segundo vehículo arranco”

Por los datos del problema, tenemos
P(A ∩B ) = 0.1;
P(A’ ∩ B ) = 0.2;

P(A’ ∩ B’ ) = 0.4

En este caso debemos hallar, la probabilidad de A. Empecemos encontrando B, en base a los datos del problema. Según el diagrama, B es la “suma” de los eventos A ∩ B y A’∩ B. Es decir, pretendemos encontrar una ecuación cuya variable sea B el cual debe estar formado por eventos mutuamente excluyentes, pero con probabilidad de ocurrencia conocidas. De allí que no expresemos a A, como la “suma” de A ∩ B y A ∩ B’, ya que no sabemos de P(A ∩ B’ ).

En efecto B = A ∩ B ∪ A ∩ B’, de donde, P(B) = P(A ∩ B)+ P(A’ ∩ B )=0.1+0.2 = 0.3

Como P(A ∪ B) = P(A) + P(B) - P(A ∩ B), y también P(A ∪ B) = 1 - P(A’ ∩ B’)

Luego P(A) + P(B) – P(AB) = 1 – P(A’ ∩ B’ ), de donde, P(A) = 1-0.4-0.3+0.1= 0.4

Debemos hallar la probabilidad de que ocurra A, dado que ya ocurrió B, es decir, P(A/B).

Por definición, P(A / B ) = P(A ∩ B) / P(B) = 0.1 / 0.3 = 1/3.

En este caso, debemos hallar P(B/A’).

Por definición de probabilidad condicional, tenemos P(B / A' ) = P(B ∩ A') / P(A') = 0.2 / (1-0.4) = 1 / 3

Ejemplo 20

Una urna contiene 8 canicas blancas y 4 canicas negras. Se extrae una muestra de tamaño 4, a) en el primer caso se devuelve la canica extraída, b) en el segundo, la canica extraída se retira. Encuentre la probabilidad de que la canica observada en la tercera extracción, haya sido blanca, si se sabe que se extrajeron 3 canicas blancas.

Solución

Definamos los eventos: A: “Se extrajeron tres canicas blancas” y B: “La tercera canica extraída es blanca”. Según esto, debemos encontrar

P(B / A ) = P( A ∩ B) / P(A)

Caso a) La muestra se selecciona con reposición
En este caso, la probabilidad de extraer una canica blanca, es la misma en cualquiera de las cuatro oportunidades, 8/12.

Ahora bien, si bien P(B/A) no ofrece ningún inconveniente en calcular por definición, sí debemos tomar nota que P(A ∩ B) y P(A), no son directos. En efecto, A consiste en extraer tres canicas blancas, de un total de 4 que contiene la muestra.

Como las canicas son indistinguibles, el número de maneras de seleccionar 3 canicas blancas de un total de 4, constituye una combinación de 4 elementos, tomados de 3 en 3, C(4,3). Como cada una de las canicas blancas puede repetirse, el número de maneras de seleccionarlas constituye una permutación con repetición, de 8 canicas tomados de 3 en 3. Con esto, tenemos una muestra, digamos BNBB; una negra se obtiene como una combinación de 4 elementos tomados de uno en uno, C(4,1). Con todo ello, el número de casos favorables a que ocurra A es n(A) = C(4,3)x 8³ x C(4,1).

El número total de maneras de seleccionar cuatro canicas del total de 12, donde cada una de ellas puede repetirse hasta cuatro veces, constituye una permutación con repetición; es decir, Pr(12, 4). Luego, la probabilidad de la ocurrencia de A se evalúa



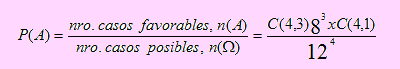
Encontremos ahora, P(A ∩ B). Una muestra de A ∩ B es “BNBB”, de los cuales tenemos 4 casos. Ahora debemos tomar en cuenta que la segunda B es fija, con lo cual, el número de maneras de obtener el grupo es C(3,2); y como por permutación obtenemos las tres canicas, el número de casos favorables de A ∩ B es n(A ∩ B) = C(3,2)x 83 x C(4,1). Luego, la probabilidad pedida será



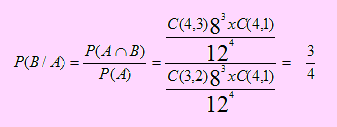
Caso a) La muestra se selecciona sin reposición
En este caso, n( Ω) está formado por grupos de 4 canicas que pueden ubicarse en cuatro formas diferentes (puede considerarse: posiciones diferentes), lo que constituye el número de permutaciones de 12 elementos tomados de 4 en 4, P(12,4).

En cuanto a la ocurrencia del evento A, “NBBB”, es una muestra de lo que se desea; en donde, las tres blancas se obtienen como C(4,3), la canica negra, C(4,1) y como estas blancas son elegidas del total de 8, esto constituye una permutación de 8 elementos tomados de 3 en 3, es decir, P(8,3). Finalmente, n(A) =. C(4,1)xP(8,3)xC(4,1),

P(A) = C(4, 1) P((, 3) C(4, 1) / P(12, 4) = 224 / 495.

En el caso de n(A ∩ B), una muestra representativa podría ser “BNBB”, donde fijamos B en la tercera posición. Estas tres canicas se pueden ordenar como C(3,2), se pueden elegir como permutaciones de 8 de 4 en 4, P(8,3) y la canica negra se elige como C(4,1); con lo cual

P(A ∩ B) = C(3, 2) P(8, 3) C( 4, 1) / P(12, 4) = 56 / 165

Luego, P(B / A ) = P(A ∩ B) / P(A) = 0.75

Ejemplo 21

IMAGINA está construyendo un edificio en un clima de aparente calma. La probabilidad de que la construcción se termine a tiempo es 17/20. La probabilidad de que no haya huelga es 3/4; la probabilidad de que la construcción del edificio se termine a tiempo, dado que no hubo huelga, es 14/15; la probabilidad de que no haya huelga y no se termine la construcción a tiempo, es 1/10.
 ¿Cuál es la probabilidad de que:

la construcción se termine a tiempo y no haya huelga?
no haya huelga, dado que la construcción se terminó a tiempo?
la construcción no se termine a tiempo, si hubo huelga?
la construcción no se termine a tiempo, si hubo huelga?



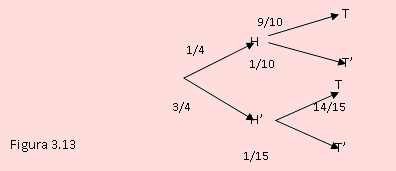
Solución

Definamos los siguientes eventos:

H: “Haya huelga”
T: “La construcción se terminó a tiempo.

Según los datos, y tomando en cuenta el diagrama:

P(T) = 17/20 , P(H’ ) = 3/4 , P(T/H’ ) = 14/15, P(H ∩ T’ ) = 1/10

Debemos hallar P(T ∩ H’). Del diagrama podemos deducir que el evento T ∩ H’ proviene del tercer ramal condicional, ya que

P(T/ H' ) = P(T ∩ H') / P(H' )
de donde P(T / H’) = 3/4x14/15 = 0.7

El evento condicional “No haya huelga, dado que la construcción se terminó a tiempo” es H’/T, por lo que, de acuerdo a lo encontrado en a)

P(H' / T ) = P( H' ∩ T) / P(T) = (7/10) / (14/15) = 14 / 17.

En este caso el evento condicional es T’/H. Por lo que

P(T' / H ) = P( H ∩ T' ) / P(H) = 0.1 / 0.25 = 0.4

Finalmente,

P(T' / H' ). Observando el diagrama, este es un dato.

Ejemplo 22

Dos amigos, A y B, participan de un juego que consiste en extraer, alternadamente, una canica de una urna que contiene 7 canicas rojas y 5 blancas. El juego se repite hasta que uno de ellos extrae una canica blanca, en cuyo caso gana y termina el juego. Si el amigo A inicia el juego, ¿cuál es la probabilidad de que gane?


Solución

Sea el G_i el evento: “El amigo A obtiene la canica blanca en el i-ésimo juego y gana”       P_i el evento: “El amigo A no obtiene la canica blanca en el i-ésimo juego y pierde”



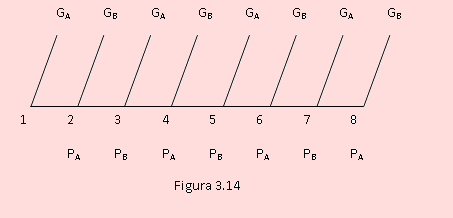
El diagrama anterior muestra la secuencia del juego. Como se puede ver, empieza jugando A; si extrae una canica blanca, gana con probabilidad P(GA) = 5/12; pierde con P(PA)=7/12, en cuyo caso juega B; si extrae una blanca gana, con P(GB) = 5/11; pierde con P(PB)=6/11.

Vamos a preocuparnos por evaluar la probabilidad de que gane A.

Sea X el evento “Gana A”. Podemos expresar a X como una unión de eventos condicionales según se indica:



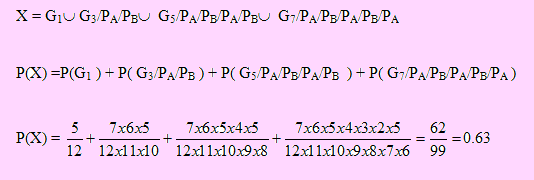
Ejemplo 23

En una ciudad, el 70% de los adultos escuchan radio; el 40% lee periódico; y el 10% ve televisión. Entre los que escuchan radio, el 30% lee periódico y el 4% ve TV; el 90% de los que ven TV, leen periódico; y sólo el 2% de la población total, lee periódico, ve TV y escucha radio. Si se elige una persona al azar, cual es la probabilidad de que lea periódico, escuche radio o vea TV vea televisión, sabiendo que lee periódico.

Solución

Sean los eventos
Pe: Leen periódico
Ra: Escuchan radio
Tv: Ven televisión

Según los datos: P(Pe) = 0.70; P(Ra) = 0.40; P(Tv) = 0.10. Por otro lado, tenemos las probabilidades: P(Pe/Ra) = 0.30; P(Pe/Tv) = 0.90; P(Tv/Ra) = 0.04; P(Pe ∩ Ra ∩ Tv) = 0.02

Aquí debemos hallar: P(Pe ∪ Ra ∪ Tv).

P(Pe ∪ Ra ∪ Tv) = P(Pe)+P(Ra)+P(Tv)-P(PeRa) – P(RaTv) – P(PeTv)+ P(PeRaTv) = 0.70 + 0.40 + 0.10 –P(Ra)P(Pe/Ra)-P(Ra)P(Tv/Ra)-P(Tv)P(Pe/Tv) +0.02 = 1.2 - .70x0.30 – 0.70x0.04 – 0.1x0.90 + 0.02 = 0.872

Debemos encontrar la probabilidad del evento “Tv/Pe”. Según esto P(Tv/Pe) = P(Tv ∩ Pe)/P(Pe) = 0.11/0.40 = 11/40.

Ejemplo 24

La urna 1 contiene x bolas blancas e y bolas negras. La urna 2 contiene z bolas blancas y v bolas rojas. Se extrae una bola de la urna 1 y se deposita en la urna 2; luego se extrae una bola de esta segunda urna. Cuál es la probabilidad de que la segunda bola extraída sea blanca?



Solución

Las figuras 3.15 y 3.16 muestran la realización del experimento y el diagrama de árbol correspondiente. Sea Y el evento: “La segunda bola extraída sea blanca”.

Según la figura 3.16, bola blanca se obtiene por dos ramas del árbol, como nos lo muestran las flechas. En la primera rama debemos obtener la probabilidad de que la primera bola haya sido blanca y la segunda sea blanca; y en la segunda rama opcional, la probabilidad de que la primera sea roja y la segunda sea blanca; es decir Y = Y ∩ B ∪ Y ∩ R. Usando propiedades, tenemos

P(Y) = P(Y ∩ B) + P( Y ∩ R) = P(B)P(Y/B) + P(R)P(Y/R)

          =(x / (x+y)) ((z+1) / (z+v+1)) + ( y /(x + y)) ( z / (z+v+1))

Ejemplo 25

Se almacenan, en un mismo depósito, dos tubos buenos con otros dos defectuosos. Se prueban los tubos de uno en uno, hasta encontrar los dos defectuosos. Cuál es la probabilidad de que

¿el último tubo defectuoso sea obtenido en la segunda prueba?
¿el último tubo defectuoso sea obtenido en la tercera prueba?
¿el último tubo defectuoso sea obtenido en la cuarta prueba?

Solución

Los elementos del espacio muestral son: DD, DBD, BDD, BDBD, BBDD, DBBD.

Sea X el evento “El segundo defectuoso se obtiene en la segunda prueba”.

P(X) = P({DD}) = (2/4)(1/3) = 1/6
Sea X el evento “El segundo defectuoso se obtiene en la tercera prueba”.
P(X) = P({DBD, BDD}) = (2/4)(2/3)(1/2) + (2/4)(2/3)(1/2) = 1/3
Sea X el evento “El último defectuoso se obtiene en la cuarta prueba”
P(X) = P({BDBD, BBDD, DBBD}) = (2/4)(2/3)(1/2)(1) + (2/4)(1/3)(2/2)(1) + (2/4)(2/3)(1/2)(1) =1/2

Siguiente sesión.