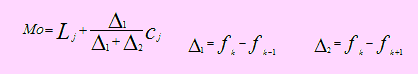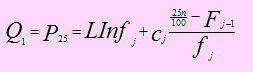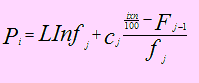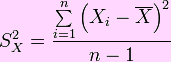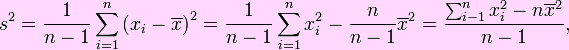2.8 ESTADÍSTICOS DE LA MUESTRA
Una vez que los datos han sido recogidos, ordenados, clasificados y han sido presentado en forma tabular o gráfica, podemos obtener algunos resultados e interpretarlos a partir de ciertos cálculos usando los datos de la muestra.
La estadística descriptiva tiene una gran cantidad de indicadores que pueden ser obtenidos usando los datos agrupados en tablas de frecuencia o no. Puesto que la forma natural de tratar los datos es mediante el concepto de variables. Cada una de las características de la población puede ser representada mediante el uso de una variable. Al seleccionar una parte de la población y obtener una muestra, los elementos que la constituyen serán los valores que toman dicha variable poblacional.
Según esto, si la variable poblacional sujeta a estudio lo constituye los ingresos de un conjunto de trabajadores de un determinado sector, una muestra de tamaño n, extraída a partir de esta población, puede ser representada mediante la serieX1, X2,…, Xn.
Esta serie de datos puede ser cualitativa o cuantitativa, como se ha dicho antes. Para obtener determinados indicadores de la muestra estos valores deben provenir de una variable cuantitativa, aunque en ciertos casos podrán ser cualitativas siempre que estén adecuadamente codificadas.
En el siguiente ejemplo, como se puede apreciar, se han obtenido una tabla de frecuencia de un conjunto de datos relativos a la opinión que tienen 80 clientes respecto a un producto de tocador.
Ejemplo 08
Abra el archivo Estad01. Los datos que se muestran constituyen las respuestas dadas por 80 clientes mujeres de una tienda de perfumerías, respecto a su preferencia por un cierto tipo de perfume.
La pregunta que se les hizo fue: Qué opina respecto a la calidad de la colonia LINUX. Las respuestas debería seleccionarlas de entre: Muy buena, Buena, Regular, Mala, Muy mala. Las respuestas que se obtuvieron se muestran en la columna C.
Cada una de estas columnas nos muestra indicadores obtenidos con los datos de la muestra. La mayoría de los clientes opinan que el producto es aceptable; la mitad de ellas están en capacidad de rechazar el producto.
Así como estos indicadores de la muestra, estudiaremos otros que nos permitirán ampliar nuestro conocimiento sobre el comportamiento de los datos de la muestra para más adelante inferir el comportamiento de toda la población desde donde se extrae la muestra.
Estos indicadores reciben el nombre deEstadísticos o Estadígrafos de la muestra, se agrupan en dos bloques según que nos permitan explicar la tendencia de los datos o la forma cómo se encuentran dispersos en la muestra: son las llamadas Medidas de tendencia central y de posición y medidas de dispersión relativa.
Pasemos a estudiar las medidas de tendencia central.
2.9 MEDIDAS DE TENDENCIA CENTRAL Y DE POSICIÓN
Ciertos estadísticos obtenidos en la muestra se denominan medidas de tendencia central porque su valor indica la posición alrededor del cual se agrupan la mayoría de los datos o muestran cierto comportamiento o tendencia de los datos.
Entre estos estadísticos tenemos:
Media Aritmética
SeaX1, X2,…, Xn una muestra extraída de una determinada población.
Si los datos no están agrupados, diremos que 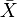 es la Media Aritmética y será obtenida mediante
es la Media Aritmética y será obtenida mediante
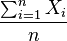
es decir,
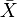 =
= 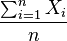
Si los datos están agrupados, entonces la media aritmética es
 donde fi representa las frecuencia absoluta en la tabla y n = ∑Xi
donde fi representa las frecuencia absoluta en la tabla y n = ∑Xi
Igualmente, si el conjunto de datos tuvieran algún peso o ponderación, la Media Aritmética Ponderada, se obtiene usando:
 donde wi representan las ponderaciones o pesos de cad uno de los datos en la tabla y n = ∑ wi
donde wi representan las ponderaciones o pesos de cad uno de los datos en la tabla y n = ∑ wi
Nota
Si todas las ponderaciones son iguales, entonces ésta no le afecta al promedio.
Ejemplo 09
Suponga que disponemos de los saldos en cuenta corriente de 10 empleados de una determinada empresa; los datos se muestran en la siguiente tabla.
Si asumimos que estos diez datos constituyen una muestra, podemos calcular el saldo promedio sumando todas los saldos y dividiendo entre 10; esto es,
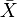 =(1756.0+748.0+15.1.0+1831.0+1622.0+1886.0+740.0+1593.0+1169.0+2125.0)/10
=(1756.0+748.0+15.1.0+1831.0+1622.0+1886.0+740.0+1593.0+1169.0+2125.0)/10
Obteniendo, 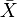 = 1497.10
= 1497.10
Interpretación
El Saldo promedio de las 10 cuentas es igual a 1497.10 unidades monetarias.
En Excel:
Función Promedio(...)
Sintaxis:
=Promedio(Valor1,Valor2,...)
donde Valor1, Valor2, ... representan un conjunto de valores, celdas o rango de celdas conteniendo dichos valores.
Esta función devuelve el promedio aritmético simple de un conjunto de datos.
En el ejemplo anterior, será suficiente ingresar en la celda que se desee el resultado, lo siguiente:
=Promedio(B10:B11)
Nota:
Otra forma de hacerlo podría ser:
=Suma(B2:B11)/10
En Excel no se requiere agrupar los datos en una tabla de frecuencias pues se puede utilizar simplemente la función promedio.
Ejemplo 10
Abra el archivo Bancordia. Obtenga el saldo promedio de todas las cuentas.
Solución
- Seleccione el rango B10:B2083 y dele el nombre Saldo.
- En D10 digite: Estadísticas
- En D11 digite: Saldo promedio = ; alinee por la derecha a esta celda
- En E11 digite: =Promedio(Saldos) y presione [Enter]
Ejemplo 11
Estando en la hoja Estadísticas de Bancordia, haga clic en el botón Mostrar que se encuentra en la celda Z2 esta macro le permitirá visualizar la hoja Ventas. Estando en la hoja Ventas y tomando en cuenta los montos de las ventas en los tres años, obtenga cada una de las estadísticas que se pide en dicha hoja.
Solución
Ingrese las siguientes fórmulas en cada una de las celdas que se indica:
En H6: =Suma(C5:C8,C10:C13,C15:C18)
En H7: =Promedio(C5:C8,C10:C13,C15:C18)
En H10: =Promedio(C5:C8)
En H11: =Promedio(C10:C13)
En H12: =Promedio(C15:C18)
En H15: =Promedio(C5,C10,C15)
En H16: =Promedio(C6,C11,C16)
En H17: =Promedio(C6,C12,C17)
En H18: =Promedio(C8,C13,C18)
Ejemplo 12
Abra su archivo Sol Bancordia el cual contiene la solución al ejemplo de la página 134. Vaya a la hoja Tabla de frecuencia. Obtenga el saldo promedio de esta muestra; es decir, obtenga la media aritmética para la tablas de datos agrupados. Luego, usando los datos de la hoja Estadísticas, obtenga el promedio de todos los saldos y comente los dos promedios.
Solución
Como los datos de la hoja Tabla de frecuencia están agrupados en una tabla de frecuencias, usaremos la fórmula del promedio para datos agrupados, que es la siguiente:

Para ello, en la celda D28 ingrese: Promedio muestral y alinearlo a la derecha.
En la celda E28 ingrese digite: =SumaProducto(F16:F24,G16.G24)/Suma(G16:G24)
En la celda H28 digite: Promedio poblacional y alinearlo a la derecha. En la celda I28 digite: =Promedio(Saldos)
Comentario:
Como puede apreciar, hemos obtenido el promedio de la muestra de 350 cuentas y hemos encontrado que el saldo promedio de la muestra (Estadístico) es (en el caso de mi solución) de 1819.2292 mientras que el promedio de todos los saldos constituye el promedio poblacional (Parámetro) y es igual a 1768.0506. Nota:
El promedio muestral es un estadístico de la muestra y se calcula con los datos de la muestra. El promedio poblacional es un indicador de la población, es un parámetro; es un valor esperado; es lo que se espera que ocurra. Este indicador poblacional no se calcula, sólo se estima. Si alguna vez se desea calcular su valor, se debe realizar un censo a la población. Ejercicio 06
Tomando en cuenta los datos del Ejemplo 02 de la página 114, obtenga las ventas mensuales promedio en los dos estados. Para ello debe abrir el archivo que se grabó al resolver dicho ejemplo.
Ejemplo 13
Suponga que los costos de producción en sucursales A, B y C de una empresa, son:
Sucursal Costo de producción (soles) Producción total
A 1,20 por artículo 500 artículos
B 1,50 por artículo 200 artículos
C 1,05 por artículo 900 artículos
Hallar el costo promedio por artículo para toda la empresa.
Solución
Puesto que el costo de producción es diferente en cada sucursal, el promedio aritmético simple (1.20 + 1.50 + 1.05r) / 3 = 1.25 no sería un promedio adecuado para ser tomado para toda la empresa. Creemos que el promedio que se requiere debe ser un promedio ponderado en donde la producción total debe ser el factor de ponderación. Para ello debemos usar la fórmula

La solución se encuentra en el archivo Media ponderada.
Ejemplo 14
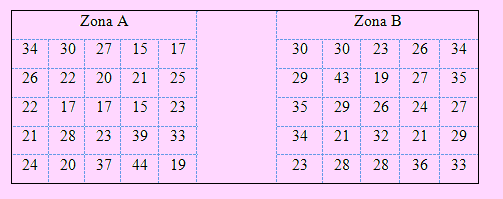
| Cálidda, una empresa distribuidora de gas natural, está interesada en analizar el número de días de morosidad en el pago de sus facturas de los clientes de dos zonas de la ciudad: ZOna A y Zona B. Para ello, de los registros de facturación por consumo mensual de los 6 últimos meses, se escogieron al azar, a 25 clientes d cada zona y se registraron el número de días que se tardan en pagar sus facturas desde el último pago realizado. Los datos recogidos de cada zona, son: |
 |
a) Obtenga la tabla de frecuencias usando el criterio de Sturges
b) Obtenga el tiempo promedio que se tardan en pagar sus facturas los clientes de las dos zonas.
c) Obtenga el tiempo promedio que se tardan en pagar sus facturas de los clientes por zona.
Solución
Abriremos el archivo Genera tabla frec. A continuación ingresamos los datos en la columna A, B ó C. En este caso se ha ingresado todos los datos en la columna A y en las columnas B y C, por zona.
a) Haciendo clic en la niñita del dibujo, generamos la tabla de frecuencias para la columna A, que sí tiene cabecera (es el nombre Pagos. El nombre de rango es Datos)
b) En la columna D25 ingresamos la fórmula:
=SumaProducto(G13:G19,H13:H19)/Suma(H13:H19)
En este caso estamos usando la fórmula:

c) Generamos la tabla de frecuencia para la columna B. Hacer clic en la niñita y seguir las peticiones de la macro.
En la columna D25 ingresamos la fórmula:
=SUMAPRODUCTO(I13:I19,J13:J19)/SUMA(J13:J19)
Volvemos a generar la tabla de frecuencia para la columna C. Clic en la niñita y responder a las peticiones de la macro.
En la columna E25 ingresamos la fórmula:
=SUMAPRODUCTO(K13:K19,L13:L19)/SUMA(L13:L19)
Mediana
Es un estadístico muestral cuyo valor ocupa la posición central de los datos; es el valor central del conjunto de los datos.
Cálculo de la mediana en datos no agrupados
Para obtener la mediana los datos se ordenan en forma creciente o decreciente.
Si el número de datos es impar: la mediana es el valor central,

Donde
Lk: Es el límite inferior de la clase de la mediana
Fk: Es la frecuencia absoluta acumulada de la clase de la mediana
fk: Es la frecuencia absoluta de la clase de la mediana.
n: Es el número de datos o tamaño de la muestra.
ck: Es la amplitud (ancho) de la clase de la mediana
Ejemplo 15
Abra el archivo Solución Bancordia.xls y calcule la mediana para todos los saldos y la mediana para la muestra a partir de los datos de la tabla de frecuencia.
Solución
En D30 digite: Mediana de la muestra, y que esté alineada por la derecha.
Determinación de la clase de la mediana: Dividimos. n/2 = 350 / 2 = 175.
Usando la columna de la frecuencia acumulada, observamos que 175 es menor que 217, que corresponde a la clase o intervalo 5 (k = 5).
Por tanto,
Lk = L5 = 1652.22 Fk-1 = F4 = 156 fk = f5 = 61 ck = c5 = 384,556
En E30 digite: =D20+(G25/2-H19)/G20*E7
Con lo cual se obtiene Me = 1772.0018
Ahora, en H30 digite Mediana de los saldos y que esté alineada a la derecha.
En I30 digite: =Mediana(MuestraSaldos). Recuerde que MuestraSaldos es el nombre de rango de todos los datos; es decir, representa a todos los datos que conforman la población; por tanto estaríamos calculando la mediana de la población. El resultado obtenido es 1723.
Compare las dos medianas que hemos encontrado: la mediana de la muestra y la mediana de la población. ¿Puede emitir algún comentario? ¿Qué representa la mediana de la muestra? ¿Qué representa la mediana de la población?
Moda
La moda es un estadístico de la muestra y representa el dato que más veces se repite. Si los datos están agrupados, la moda se encuentra en el intervalo o clase en el cual la frecuencia absoluta es la mayor.
La fórmula de la moda cuando los datos están agrupados, es la siguiente:
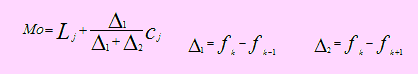
Ejemplo 16
Obtenga la moda para la tabla de frecuencia de Solución bancordia.
Solución
Primero determinaremos el intervalo a la cual pertenece la moda: Para ello es suficiente observar el intervalo que contiene la mayor frecuencia absoluta. Observando esta columna vemos que la mayor frecuenta es 64, que se encuentra en el 4to. Intervalo; por tanto
Lj = L4 = 1267.67 fk = f4 = 64 fk+1 = f5 = 61 fk-1 = f3 = 51
Ahora digite en D32: Moda de la muestra; y que esté alineada a la derecha
En E32, digite: =D19+(G19-G18)/((G19-G18)-(G19-G20))
El valor de la moda es: 1268.9667
En H32 digite: Moda de todos los saldos, que esté alienado por la derecha
En I32 digite: =Moda(MuestraSaldos). El valor obtenido será 1494.
Observación
| Resumen Estadístico |
| Estadístico |
Muestra |
Población |
| Media aritmética |
1819.23 |
1768.05 |
| Mediana |
1772.00 |
1723.00 |
| Moda |
1268.23 |
1494.00 |
Según estos resultados podemos decir que el conjunto de los saldos evaluados en la muestra presenta una asimetría positiva puesto que el promedio es superior al valor central de los datos (mediana); es decir, la tendencia central de los datos está por encima del 50% inferior de los mismos. El mismo comportamiento se aprecia con todos los saldos. ¿Qué significa asimetría? Lo veremos más adelante.
Media Geométrica
La media geométrica permite obtener un promedio de un conjunto de datos. Es usado de manera particular en el cálculo de la tasa de variación promedio para un número determinado de períodos de una serie de números índice.

Ejemplo 17
La figura anterior muestra el precio de un producto durante los 12 meses. La segunda columna contiene la tasa de variación mensual.
La función promedio aplicada a los precios (=Promedio(A2:A13)) devuelve 24.25 La función Media.Geom(A2:A13) aplicada a los precios, devuelve 24.25
La función Media.Geom(A2:A13) aplicada a la tasa de variación mensual (en este caso hemos calculado la columna C, 1+tasa) devuelve la tasa media de variación mensual igual a 0.945788063.
En la figura aparece también otra forma de calcular la tasa media de variación mensual, lo que valida el uso de la media geométrica para este cálculo.
Cuartiles y Percentiles
Estos indicadores dividen al conjunto de datos en cuatro segmentos o grupos iguales, cada uno de los cuales incrementa en 25% de los datos cuando se acumulan.
En el caso de los percentiles, cada uno de ellos divide al conjunto de datos en 100 segmentos o grupos iguales, cada uno de los cuales incrementa en 1% de los datos cuando se acumulan.
Hay 3 cuartales.
Y si hablamos de percentiles? Habrá 99 percentiles.
Interpretación de los cuartiles
Q1 representa el valor máximo del 25% de los datos más pequeños. Del mismo modo, se puede afirmar que el 75% de los mayores datos son superiores al valor Q1.
Q2 representa el valor máximo del 50% de los datos. Dicho de otra manera, el 50% de los datos son superiores al valor Q2. Este cuartil coincide con la mediana.
Q3 representa el valor máximo del 75% de los datos. Igualmente puede decirse que el 25% de los datos son superiores a él.
En cuanto a los percentiles: En realidad debiéramos hablar sólo de percentiles pues si éstos dividen a los datos en 99 grupos o segmentos, entre ellos están los llamados cuartiles, deciles (que dividen a los datos en 9 partes), los quintiles, etc.
El cuartil 1 es el mismo que el percentil 25 pues representan el 25% inferior de los datos más pequeños. Dicho de otra manera, representan el 75% superior de los datos de mayor valor.
Del mismo modo, el percentil 35 representa el valor máximo del 35% de los datos inferiores a él.
El valor del primer cuartil se obtiene usando:
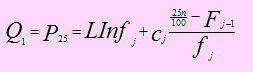
Para determinar el intervalo al cual pertenece el primer cuartil, se debe obtener el valor de n/4 o 25n/100 como percentil 25. El valor del tercer percentil se obtiene con:

Como en el caso del primer cuartil, para determinar el intervalo al cual pertenece el tercer cuartil, se debe obtener el valor de 3n/4 o 75n/100 como percentil 75.
El valor de un percentil cualquiera Pi se puede obtener usando la fórmula:
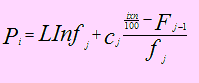
Para el cual, se debe ubicar el intervalo mediante Fj ≤ i(n)/100 ≤ F j-1
En MS Excel
Los cuartiles se obtienen mediante la función =Cuartil(Arg1, Arg2) donde Arg1 representa el rango o lista de los datos y Arg2 es un valor numérico que indica el número de cuartil que se desea obtener.
En general, un percentil cualquiera se obtiene usando la función:
Percentil(Datos, n)
donde Datos representa el rango o lista de los datos y n es el número real que indica el percentil que se desea obtener; 0 [ n [ 1. n debe estar en porcentaje.
Si se desea obtener el percentil 1, n = 0.1; si se desea el percentil 25; n = 0.25, lo cual debe ser equivalente a obtener el cuartil 1.
Ejemplo 18
El número de panes semanales que un grupo de 110 familias de una manzana consume en el desayuno se muestra en la siguiente tabla:
| Número de latas |
Número de consumidores |
| [20 , 30 ) |
25 |
| [30 , 40 ) |
20 |
| [40 , 50 ) |
35 |
| [50 , 60 ) |
15 |
| [60 , 70 ) |
15 |
a) ¿Más del 50% de los entrevistados tienen un consumo semanal de panes en el desayuno, superior al promedio? Fundamente su respuesta.
b) ¿Cuál es el número mínimo de panes adquiridos semanalmente para el desayuno por el 25% de familias que más panes adquieren?
c) ¿Cuál es el número máximo de panes semanales consumidas por el 15% de las familias que menos panes consumen?
d) ¿Cuál es el número de panes semanales consumido por el 50% de las familias?
e) ¿Cuál es el porcentaje de familias consumen panes por encima de 55 semanalmente?
Solución
Abra un libro vacío. Ingrese los datos en las columnas A, B y el número de consumidores (frec. absoluta) en la columna D, la cabecera puede tener el mismo formato de la hoja 1 del archivo Percentiles.xls. Calcule la columna del punto medio digitando en C2: =(A2+B2)/2; luego copie hacia las siguientes filas. A continuación obtenga la columna de la frecuencia acumulada digitando en E2: =D2. En E3 digite: =E2+D3. Luego copie hacia abajo.
a)
En B9 ingrese “Promedio = “. En B12 ingrese: “Mediana = “. En C9 ingrese =SumaProducto(C2:C6,D2:D6)/Suma(D2:D6) Calculemos la mediana: Como n/2 = 110/2 = 55 nos permite afirmar que la mediana se encuentra en el intervalo (40, 50), entonces Linf = 40; amplitud del intervalo = 10; Fj-1 = 45; fj = 35. Usando la fórmula de la mediana, ingresamos en C12: =A4+10*(110/2-E3)/D4.
Encontramos que el promedio es 42.727273 y la mediana es 42.857143. Puesto que el 50% de los datos están por encima del promedio, desde el promedio habrá más del 50% ya que su valor es inferior a la mediana. En consecuencia la respuesta es Sí.
b)
En este caso se pide encontrar el valor del percentil 25 o su equivalente, el primer cuartil. Puesto que n/4 = 25*n/100 = 27.5, entonces el intervalo al cual pertenece el primer cuartil o el percentil 25 es (30, 40). Esto implica que el LInf = 40; amplitud = 10; Fj-1 = 25 y fj = 25. Luego en B15 ingresamos: Primer cuartil; en C15, la fórmula: =A3+10*(110/4-E2)/D3.
Dejamos las siguientes dos preguntas como ejercicio.
Ejemplo 18: De generación de tabla de frecuencia y cálculo de estadísticos
Dado un conjunto de datos que se ingresa en una de las primeras columnas de una hoja de cálculo, obtener una tabla de frecuencias y los estadísticos principales.
Solución
Abra el archivo Generador de tabla frec.La extensión xlsm indica que se trata de un libro creado en la versión 2007 del Excel y que contiene macros. Sugerimos al lector que analice la codificación de esta macro y vea que muchas herramientas estadísticas podemos construirlas de la misma forma. Sólo requiere voluntad, ingenio y un poco de esfuerzo y dedicación.
Ingrese sus datos en la columna A, B o C de cualquiera de las hojas. Si hubiera datos en la columna elegida, bórrelos e ingrese los suyos. Haga clic en la imagen de la niñita. Cuando pida nombre de la hoja, digite el nombre de la hoja donde tiene sus datos. A continuación digite la columna donde ingresó sus datos; digite S si le puso nombre de columna (o cabecera) y finalmente, ingrese el número de intervalos que desea usar. Si desea usar la fórmula de Sturges, digite 0. En cada dato que ingrese, presione [Enter] o haga clic en [Aceptar]. Para terminar, pueden abrir los archivos:Gráfico con macros o Ice calc v2
Y podrán encontrar en ellos lo que se puede hacer en Excel con macros y VBA.
Diagrama de Caja
Este es un tipo de gráfico que nos permite saber si en la muestra existe datos perdidos “data missing” así como la simetría de los datos y el sesgo que pudieran tener.
Para ello el gráfico presenta una caja tomando como lados extremos a los cuartiles primero y tercero. La mediana es un segmento vertical que divide a la caja no siempre en partes iguales. Es ella la que indica si los datos están distribuidos simétricamente o no.
Para conocer el diagrama de caja en un ejemplo y analizar su estructura, abra el archivo Graf 03, vaya a la hoja Diagrama de caja.
Comentario:
Si suponemos que los datos corresponden a una población de ingresos de 2156 trabajadores, podemos observar lo siguiente:
Los ingresos no son simétricos pues presentan cierto sesgo a la derecha. Esto lo apreciamos ya que el 50% de los empleados tienen ingresos superiores al promedio: Promedio = 2333.54 soles; Mediana = 2326.82 soles.
Los extremos del mayor rectángulo representan los ingresos mínimo y máximo de los datos. Esto quiere decir que, los ingresos de los trabajadores varían de un ingreso mínimo de 487.37 hasta 4414.95 con un rango de variación de 3927.58. En otras palabras, la dispersión de los ingresos, alrededor de la media, es de 655.07 soles.
La línea horizontal que une los extremos de dicho rectángulo representan los “bigotes”. Valores fuera de esta línea indicarían datos perdidos.
2.10 MEDIDAS DE DISPERSIÓN
Estos estadísticos o indicadores de la muestra nos permiten medir o cuantificar la forma cómo se distribuyen los datos en términos de su separación o aglomeración alrededor de algún estadístico de posición central.
Según esto, podemos saber cuán separados o dispersos están respecto de la media, o qué porcentaje de variabilidad (homogeneidad) presentan los datos.
Entre las medidas de dispersión más frecuentemente usadas tenemos:
Rango
Es un estadístico obtenido como la diferencia entre los valores máximo y el mínimo de los datos. Puede ser interpretado como la diferencia entre dichos valores.
Si se tratara de ingresos de un conjunto de trabajadores nos mediaría la brecha entre los que menos ganan y los que más ganan. A mayor valor del rango, mayor la diferencia.
Rango = Max(Datos) – Min(Datos)
Ejemplo
Veamos el siguiente conjunto de datos, que representan los jornales diarios de los trabajadores de las empresas AcerSa y PocSa.
| AcerSA |
16.5 |
16.0 |
15.9 |
16.3 |
16.1 |
15.3 |
16.8 |
15.3 |
13.2 |
16.5 |
14.4 |
15.2 |
15.3 |
| AcerSA |
22.4 |
19.1 |
15.9 |
20.4 |
19.2 |
15.4 |
9.8 |
10.5 |
22.6 |
11.8 |
7.2 |
20.7 |
7.8 |
Podemos comprobar que el promedio de los ingresos diarios es de 15.6 soles.
Del mismo modo, la mediana en ambos casos es 15.9.
En ambas empresas el 50% de los trabajadores tienen ingresos diarios superiores al ingreso promedio.
¿Podemos afirmar que en las dos empresas los ingresos diarios son similares; es decir, son similares, coherentes u “homogéneos”?
Calculemos el rango
ACERSA: Rango = Max(Datos) – Min(Datos) = 16.5 – 13.2 = 3.3
POCSA: Rango = 22.6 – 7.2 = 15.4
En Excel:
Abra el archivo Dispersiones. En la hoja dispersión, en la celda E4, calcule el rango ingresando la fórmula =Max(Acersa) – Min(Acersa). Haga lo mismo para obtener el rango de Pocsa en E7.
Observamos que los jornales en Acersa son menos diferenciados que los de Pocsa. Luego no podríamos afirmar que los ingresos son similares u “homogéneos” en ambas empresas.
Rango Intercuartílico
El rango intercuartílico permite conocer la diferencia entre el primer y tercer cuartil y permite saber los límites en los que se encuentra el 50% central de los datos.
Tomando en cuente el ejemplo anterior y usando la misma hoja Dispersión, haga clic en el botón RIntq para visualizar el cálculo del rango intercuartílico en el caso de Acersa. Obtenga dicho rango para los de Pocsa.
Varianza
Este indicador, al lado de la media aritmética, constituyen los estadísticos más utilizados y de mayor importancia en la estadística.
Permite conocer el promedio de la diferencia cuadrática entre el conjunto de los datos con respecto a la media aritmética, estadístico de la muestra. Indica la magnitud de la variabilidad de los datos.
Nota
1. La varianza se representa por s².
2. En el caso de la varianza poblacional, la diferencia se mide respecto a la media poblacional.
3. A pesar de su importancia en la estadística, la interpretación de la varianza es algo forzada pues si se tratara de la varianza de los sueldos de un conjunto de trabajadores, ésta estaría medida en soles cuadrados.
Cálculo de la varianza:
Para calcular la varianza de un conjunto de n datos, use la siguiente fórmula:
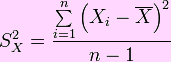
La siguiente forma constituye la forma práctica y de fácil uso:
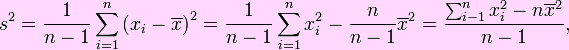
En Excel
La función que permite calcular la varianza es
Var(Arg1)
donde Arg1 puede hacer referencia a una serie de valores, un rango o lista de datos.
Desviación estándar
La desviación estándar es la raíz cuadrada de la varianza. Permite medir la cantidad de dispersión que existe entre los datos, respecto a la media aritmética. Mide la dispersión absoluta pues al provenir de una raíz cuadrada de la varianza, las dispersiones negativas han sido convertidas en positivas.
En Excel
La función que permite obtener la desviación estándar es
DesvEst(Arg1)
donde Arg1 puede hacer referencia a una serie de valores, un rango o lista de datos.
Ejemplo 19
Tomando en cuenta los datos de las empresas Acersa y Pocsa, en el ejemplo anterior, ¿los valores de las desviaciones estándares confirman la observación hecha con el rango?
En la hoja Dispersión del archivo Dispersiones calculamos la varianza ingresando en E17: =Var(Acersa) y en E18: =Var(Pocsa).
Calcule la desviación estándar en E22 y E23.
¿Qué comentario haría en ambos casos?
Aquí un posible comentario:
Los jornales diarios de los trabajadores de Acersa presentan están menos dispersos que los de Pocsa; consecuentemente, la variabilidad es mucho mayor en Pocsa. Observe el gráfico en la hoja y podrá apreciar cuán separados (dispersos) se encuentran los jornales en una y otra empresa.
Medidas de dispersión relativa: Coeficiente de Variación
Este estadístico permite medir o cuantificar la variabilidad de los datos. Nos indica si esta variación presenta mucha o poca variabilidad.
Se define como la razón entre la desviación estándar y la media aritmética. Por lo general la interpretación se da en forma porcentual.

Como se puede apreciar, si la media o promedio es negativo, el coeficiente es negativo; esto significa que dicho coeficiente mide la dispersión relativa.
La medida de la variabilidad de los datos nos permite afirmar si son homogéneos o no (heterogéneos).
En el caso de los datos de los ingresos diarios de Acersa y Pocsa, podemos apreciar en la hoja Dispersión, que los jornales de los trabajadores de Acersa son más homogéneos que los de Pocsa ya que el coeficiente de variación de Acersa es del 6.32% mientras que el de Pocsa es 35.84%.
2.11 ASIMETRÍA
El comportamiento de los datos en cuanto a su posición y su variabilidad se puede medir mediante los estadísticos de asimetría.
Estos miden tanto la inclinación de los datos así como su dispersión. Entre las medidas de asimetría más conocidos están el Coeficiente de Pearson y las medidas de Curtosis y Apuntamiento.
Mencionaremos sólo al Coeficiente de Pearson. Primer coeficiente: CA = 3(Media - Mediana ) / s
Mide la razón entre a media y la mediana y la desviación estándar.
Segundo coeficiente: CA = (Q1 + Q3 - 2 Mediana) / (Q3 - Q1)
Ambos coeficientes pretender decirnos si los datos están sesgados respecto a su valor central.
Si CA = 0 ==> Los datos son simétricos.
Si CA < 0 ==> Los datos se encuentran inclinados hacia la izquierda o están sesgados a la derecha; por el contrario, son sesgados a la derecha, si CA > 0.
Ejemplo 20
En el ejemplo que estamos comentando se ha obtenido el coeficiente de asimetría de cada grupo de datos en las celdas:
En E34 digite:
=3*(PROMEDIO(Acersa)-MEDIANA(Acersa))/DESVEST(Acersa)
En E35 digite:
=3*(PROMEDIO(Pocsa)-MEDIANA(Pocsa))/DESVEST(Pocsa)
Se puede apreciar que la asimetría de los jornales en ambos casos es negativa. Los datos presentan un sesgo hacia la izquierda; es decir, los trabajadores con jornales más bajos presentan dispersión, están más alejados del promedio.
En resumen:
Con los resultados obtenidos al calcular los estadísticos de posición o de tendencia central y los de dispersión, podemos conocer el comportamiento y variabilidad de los datos.
Si un gran porcentaje de los datos son inferiores al promedio tenderán a tener un coeficiente de asimetría negativo mientras que si la mayor cantidad de los datos están por encima de la media, el coeficiente de asimetría será positivo.
Ejemplo 21 (Demostrativo desarrollado en Excel)
High Quality es una institución dedicada a otorgar certificaciones de calidad ISO 9001 a empresas de bienes y servicios. La Real S.A. está en proceso de evaluación por esta institución y una de las tareas es medir la satisfacción del personal de la empresa mediante una prueba con escala de 0 a 100 puntos. Los 40 trabajadores que laboran en la sede principal obtuvieron las siguientes puntuaciones:
74 89 82 83 67 81 68 85 81 72
71 74 60 64 72 84 66 84 69 81
69 66 93 63 98 70 95 82 81 80
88 80 85 85 72 81 90 89 80 87
a) Obtenga una tabla de distribución de frecuencias e interpreta algunos valores de dicha tabla
b) ¿Cuáles son los dos valores entre los cuales se encuentra el 50% las calificaciones obtenidas por dichos trabajadores?
c) ¿Cuál es la máxima calificación obtenida por el 20% de los trabajadores con menos calificación?
d) ¿Cuál debería ser la mínima calificación de un trabajador para que se encuentre en el quinto superior?
e) Obtenga la calificación media y luego de compararlo con la mediana de las calificaciones, diga si las calificaciones presentan un sesgo y hacia dónde.
f) ¿Las calificaciones de los 40 trabajadores presentan cierto grado de homogeneidad?
g) ¿Cuál es la dispersión absoluta de las calificaciones de los trabajadores?
h) ¿Compare el valor del Rango y el rango intercuartílico y diga cuál de ellos proporciona una mejor interpretación?
i) Obtenga el grado de asimetría de las calificaciones e interpreta su valor.
Solución
Para resolver las preguntas por Excel, ingrese los datos a la primera columna colocando en A1: Puntaje. Luego debe darle el nombre Puntaje al rango A2:A41.
Ante todo, ingresamos los datos en la columna A, a partir de la celda A2. En A1 colocamos Calif como nombre de la variable puntuación obtenida por un trabajador. Haga que la columna tenga una amplitud de 7.71. Que el rango de datos se llame Calif. ¿Cómo? a) Procedimiento: Rango C9:I9; combinar celdas; usar borde de cuadro grueso. Ingresar el texto:
Tabla de distribución de frecuencias.
| En C2 |
n = |
=Contar(Calif] |
| En C3 |
Min = |
=Min(Calif] |
| En C4 |
Máx = |
=Max(Calif] |
| En C5 |
Rango = |
=C4 - C3] |
| En C6 |
Nro intervalos = |
=Entero(1+3.32*Log10(C2)+0.5) |
| En C7 |
Amplitud = |
=C4/C5 |
En el rango C10:H10 ingrese:
Linf LSup PtoMedio fi Fi hi Hi
Cálculo de los límites de cada intervalo
En D2: =Contar(Calif)
En D3: = Min(Calif)
En D4= =Max(Calif)
En D5: = D4-D3
En D6: =ENTERO(1+3.32*LOG(D2)+0.5)
En D7: =D5/D6
En C11: =Min(Calif)
En D11: =C11+D$7
En C12: =D11
En D12: =C12+D$7
Copiar el rango C12:D12 y pegarlo en el rango C13:D16
Cálculo del punto medio:
En E11: =(C11+D11)/2
Copiar esta fórmula y pegarlo en el rango E12:E16.
Haga que el punto medio tenga dos decimales.
Obtención de la frecuencia absoluta:
- Seleccionamos el rango F11:F16 y sin deshacer esta selección,
- Ingresamos la fórmula: =Frecuencia(Calif,D11:D16)+0.001.
Luego, teniendo presionadas las teclas [Ctrl]+ [SHIFT], presionamos [Enter].
Nota:
Le añadimos 0.001 a la fórmula de D16 para que la función frecuencia incluya al extremo superior del último intervalo. Cada uno de los intervalos esabierto por la derecha. Luego obtenemos la suma de las frecuencias en F17.
Cálculo de las otras frecuencias:
En G11: =F11; En H11: =F11/$F$17; En I11: =H11
En G12: =G11+F12; En H12: =F12/$F$17; En I12: =I11+H17
Copiar el rango G12:I12 y pegarlo en el rango G13:I16
La tabla es la siguiente:
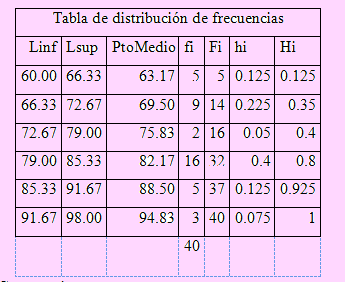
Comentarios:
- Hubo 16 trabajadores de la empresa cuya puntuación estuvo entre 79 y 85.33.
- Del mismo modo, 32 trabajadores tuvieron una puntuación por debajo de 85.33
- A 25 trabajadores se les dio una calificación entre 79 y 91.67.
- El 40% de los trabajadores tuvieron una calificación inferior a 70.
La tabla se encuentra en el archivo Ej prob01.
b) El siguiente esquema muestra los dos valores que debemos hallar, entre los cuales se encuentra contenido el 50% de los datos.
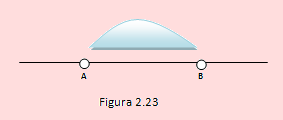
Si en el centro hay 50%, los segmentos exteriores contienen 25% de datos cada uno; por tanto, se trata de obtener los valores del primer y tercer cuartil.
Primer cuartil:
El valor que se requiere para ubicar el intervalo donde se encuentra el primer cuartil es n/4; es decir 40/4 = 10. Usando la columna F, el intervalo es el segundo.
A=66.33+6.3333*(40/4-5)/9 = 69.8485
En Excel:
Se deberá usar la función Percentil(RangoDeDatos,k) donde k debe estar expresado en porcentaje. Si se desea el percentil 20, k = 0.20.
Para obtener el primer cuartil:
=Percentil(Puntaje,0.25) = 70.75
Tercer cuartil:
En este caso ubicaremos 3n/4 = 3(40)/4 = 30 usando la frecuencia acumulada. Esto indica que el intervalo donde se encuentra el tercer cuartil es el cuarto; luego
B=79.00+6.3333(30-16)/16 = 84.5416
En Excel:
=Percentil(Puntaje,0.75) = 85
c) El 20% de los trabajadores con menor calificación indica que debemos hallar el percentil 20.
Esto significa que debemos ubicar primero el intervalo donde se encuentra dicho valor. Puesto que 20n/100 = 20(40)/100 = 8, entonces el percentil 20 se encuentra en el segundo intervalo. Por ello, P20 =66.33+6.3333(8-5)/9 = 68.44
Esto significa que el 20% de los trabajadores tuvieron una puntuación por debajo de 68.44; consecuentemente, la puntuación mínima del 80% de los trabajadores fue de 68.44.
En Excel:
=Percentil(Puntaje,0.20) = 69
d) Contrario a la pregunta anterior, debemos obtener el percentil 80, ya que al 20% superior, le corresponde el 80% de los valores acumulados hasta el valor de dicho percentil. De manera que, puesto que 80(40)/100 = 32, cae en el cuarto intervalo, y esto indica que, el 80% de los datos alcanzan un valor máximo de 32; diremos que ésta es la mínima calificación del 20% de los trabajadores.
P80 = 79.0+6.3333(32-16)/16 = 85.33
Resuelto por Excel:
=Percentil(Puntaje,0.80) = 85.4
e) La solución a esta pregunta la daremos hallando primero el promedio y mediana. Cálculo del promedio: Usando los resultados en Excel (archivo Ej prob01)
Promedio = 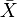 = (SUMAPRODUCTO(E11:E16,F11:F16))/(SUMA(F11:F16)) = 78.368
= (SUMAPRODUCTO(E11:E16,F11:F16))/(SUMA(F11:F16)) = 78.368
Cálculo de la mediana: Usando la tabla mostrada líneas arriba,
Me=79.0+6.3333(20-16)/16=80.5833
En consecuencia, las calificaciones de los trabajadores presentan una asimetría negativa y están sesgadas a la izquierda.
En Excel:
=Mediana(Puntaje) ==> 81
f) Para responder a esta pregunta debemos hallar el coeficiente de variación; y para calcularlo necesitamos obtener primero la varianza en datos agrupados.
Cálculo de la varianza:
Usando el archivo Ej prob01, s²= (SumaProducto(E11:E16,E11:E16,F11:F16)-40(78.368²))/(40-1)=88.0285754
De donde s = 9.38235447
Finalmente CV(X)= 9.38235447/78.368=0.11972175
Puesto que las calificaciones presentan una variabilidad del 11.97%, diremos que son homogéneas.
Resuelto en Excel
=Var(Puntaje) = 89.025
g) La dispersión absoluta se mide utilizando la desviación estándar. Puesto que la desviación estándar es 9.383, entonces diremos que las calificaciones presentan una dispersión de 9.383 respecto de la calificación promedio.
En Excel:
=DesvEst(Puntaje) = 9.435306
h) Según los resultados obtenidos en el libro mencionado,
Rango = 38
RIQ = Rango inercuartílico = Q3 – Q1 = B – A = 84.5416 – 69.8485 = 14.6931 Ambos indicadores son complementarios. Mientras el rango nos indica la dispersión que hay entre la mínima y máxima calificación, el rango intercuartílico nos indica qué tan dispersos están el 50% de las calificaciones centrales.
i) Calcularemos el coeficiente de asimetría.
Esto es, CA= (3(Media-Mediana))/s=(3(78.3667-80.5833))/9.383=-0.7087
Esto refuerza a una conclusión anterior (g); es decir, presentan un grado de asimetría negativo.
En Excel
=Coeficiente.Asimetria(Puntaje) = -0.064944
2.12 PROBOLEMAS PROPUESTOS
1. BATCOM es una empresa líder en la venta de baterías para diferentes tipos de vehículos. El gerente de ventas Los siguientes datos corresponden a la vida útil (en años) de 48 baterías similares de automóvil de la marca POWER. El fabricante garantiza que estas duran tres años.
4.1 3.5 4.5 3.2 3.7 3.0 2.6 3.4 1.6 2.2
3.1 3.3 3.8 3.1 4.7 3.7 2.5 4.3 3.4 3.6
2.9 3.3 3.9 3.1 3.3 3.1 3.7 4.4 3.2 4.1
2.0 3.4 4.7 3.8 3.2 2.6 3.9 3.0 4.2 3.5
1.7 2.3 2.6 3.2 3.5 4.3 4.8 4.0
Los datos ya han sido ingresados en la primera columna del archivo Ej prob01. Resuelva cada una de las siguientes preguntas:
a) Que el nombre del rango de los datos se llame Tvida.
b) Obtenga una tabla de distribución de frecuencias e interpreta algunos valores de dicha tabla
c) ¿Cuáles son los dos valores entre los cuales se encuentra el 50% de las baterías de la muestra?
d) ¿Cuál es el máximo tiempo de vida del 20% de las baterías de la muestra?
e) ¿Cuál debería ser el mínimo tiempo de vida de una batería para que se encuentre en el quinto superior?
f) ¿Qué porcentaje de baterías tienen un tiempo de vida máximo de 4 años?
g) Obtenga la duración media y luego de compararlo con la mediana de la duración de las baterías, diga si la duración de las baterías presentan un sesgo y hacia dónde.
h) ¿Las calificaciones de las 48 baterías presentan cierto grado de homogeneidad?
i) ¿Cuál es la dispersión absoluta de la duración de las baterías?
j) ¿Compare el valor del Rango y el rango intercuartílico y diga cuál de ellos proporciona una mejor interpretación?
k) Obtenga el grado de asimetría de la duración de dichas baterías.
2. Copie los datos del archivo Ej prob01 y péguelos en una de las hojas del archivo Genera tabla frec 1.
En la primera fila de dicha columna debe ponerle un nombre y todos los datos que conforman la muestra deben tener un nombre de rango. Luego haga clic en la imagen de la niñita de las otras hojas e ingrese los datos de manera adecuada a fin de obtener todos los estadísticos de la muestra.
3. Haga lo mismo que en el problema 3 pero usando el archivo Ej Prob02.
4. Haga clic en el botón [Crear histograma] para crear un gráfico con los datos de la tabla del archivo Ej Prob01. Tome nota que los valores del eje X son los límites superiores de cada intervalo.
5. Copie el módulo MacroGraff01 del archivo anterior. Abra el archivo EjProb02. Inserte un módulo en el editor y pegue lo copiado. Luego modifique los rangos de la serie de datos así como los del eje X, de acuerdo a los que corresponden a la tabla de frecuencia del archivo EjProb02.xlsm. Vuelva a grabar el archivo.
6. Grabe otra macro a fin de crear otro gráfico con las mismas características con los datos del archivo EjProb02.xlsm. Inserte un botón de formulario y asígnele la macro que ha creado.
7. Diseñe y codifique un formulario que permita el ingreso de datos a una hoja de un determinado libro.
Siguiente sesión.
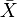 es la Media Aritmética y será obtenida mediante
es la Media Aritmética y será obtenida mediante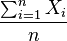
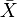 =
= 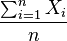
 donde fi representa las frecuencia absoluta en la tabla y n = ∑Xi
donde fi representa las frecuencia absoluta en la tabla y n = ∑Xi donde wi representan las ponderaciones o pesos de cad uno de los datos en la tabla y n = ∑ wi
donde wi representan las ponderaciones o pesos de cad uno de los datos en la tabla y n = ∑ wi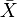 =(1756.0+748.0+15.1.0+1831.0+1622.0+1886.0+740.0+1593.0+1169.0+2125.0)/10
=(1756.0+748.0+15.1.0+1831.0+1622.0+1886.0+740.0+1593.0+1169.0+2125.0)/10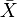 = 1497.10
= 1497.10