Así como una tabla de distribución de frecuencias nos permite “saber” lo que los datos quieren “decirnos” en forma cuantitativa, así también el Análisis Exploratorio de Datos contiene diversos tipos de gráficos que nos permitirán obtener resultados similares a los que proporciona una tabla de frecuencias y más aún, obtener información previa tanto para validar los datos así como para saber qué herramientas estadísticas pueden ser usados en el análisis de los datos en cuestión.
Decíamos que es una concepción moderna ya que tradicionalmente el análisis cuantitativo de los datos ha precedido al análisis gráfico. El modelo clásico, que puede ser determinista o probabilista (incluyendo el modelo bayesiano), impone el modelo sobre los datos, bajo determinados supuestos; por ejemplo, el modelo de regresión lineal o el análisis de varianza o algunas herramientas del análisis multivariado, supone la existencia de un determinado tipo de variable con distribución normal. El Análisis Exploratorio de los Datos (EDA), deja que los datos sugieran un determinado modelo al cual se ajustan.
Los siguientes esquemas traducen con mayor claridad, lo que queremos decir:

Técnicas del EDA
Las técnicas del Análisis Exploratorio de Datos son esencialmente gráficas. Por ello no son rigurosos, pueden ser subjetivos y un investigador puede tener diferentes apreciaciones que otro, pero entre los experimentados, la conclusión será la misma.
Si bien estas técnicas no son rigurosas y pueden ser subjetivas, los modelos construidos a partir del análisis realizado sobre los gráficos, producirán modelos rigurosos, formales y adecuados al problema, mucho antes que las técnicas clásicas.
Entre las diversas técnicas que aquí tomaremos en cuenta tenemos:
Histograma de frecuencias
Este tipo de gráfico es usado para mostrar gráficamente los cuatro tipos de frecuencias: absolutas, absolutas acumuladas, relativas y relativas acumuladas.
Permite saber el número de datos o porcentaje (frecuencia absoluta o relativa) que se encuentran en un grupo (intervalo) así como la frecuencia o porcentaje acumulado de datos hasta un determinado valor máximo.
Nota importante:
Todos los ejemplos que desarrollemos en este capítulo, serán desarrollados usando el MS Excel 2003, pero que también pueden ser resueltos con la versión 2007, 2010 y 2013, sin ninguna dificultad. En algunos casos lo repetiremos usando MS Excel 2007.
Ejemplo 03
Construya un histograma de frecuencias para la tabla de frecuencias contenida en el archivo bancordia.
Procedimiento.
- Abrimos el archivo Sol Bancordia. Nos ubicamos en la hoja Tabla de Frecuencia.
- Los datos contenidos en ella son los siguientes:

- Seleccionamos el rango de las frecuencias absolutas: G16:G24
- Hacemos clic en el icono del asistente para gráficos, tipo
de gráfico: Columnas, subtipo: Columna agrupada. Clic en [Siguiente]
- Hacemos clic en la pestaña [serie]. En [Nombre] ingrese: fi Hacemos clic en el cuadro de texto de [Ró en el eje ... ] seleccionamos el rango E16:E24.
Hacemos clic en [Siguiente]
- En la pestaña [Titulos], en [Titulo del gráfico] digitamos: Histograma de frecuencias de los saldos. Hacemos clic en el botón [Finalizar]
- Usando el botón derecho en el eje de categorías, modifique el tamaño de fuente en 6, ingresando por [Formato de ejes ]. Modifique también la inclinación a 45º ingresando a la ficha [Inclinació]. Haga lo mismo con el eje vertical para que el tamaño de fuente sea igual a 6.
- Haciendo uso del botón derecho sobre una de las barras y usando [Formato serie de datos], ingresamos a la ficha [Opciones]. El [Ancho de rango] lo dejamos en 0.
- Ahora hacemos clic en la parte sombreada y luego la tecla [Supr], borramos también las líneas horizontales haciendo clic en una de ella y luego en [Supr]
- Finalmente, usando el botón derecho del ratón, sobre el fondo del gráfico, seleccionando [Opciones de gráfico] podemos seleccionar el color de fondo que se desee.
Recuerde que los datos usados para generar el presente histograma no provienen de los mismos datos que aparecen en el archivo en uso pues son dos muestras diferentes. El histograma resultante se muestra en la figura 2.13

Construcción del histograma usando MS Excel 2007 (el procedimiento es el mismo con la versión 2010 y 2013):
Procedimiento:
- Luego de abrir el libro SolBancordia.xls, activamos la hoja Tabla de frecuencia; seleccionamos el rango de las frecuencias incluyendo la celda con fi para que sirva como leyenda.
- Usamos la secuencia: [Insertar] - del grupo Gráficos [Columna]. En columna en 2-D, seleccionamos la primera: [Columna agrupada].
- Modificación del histograma: Para obtener la frecuencia absoluta: [Botón derecho en cualquier barra ] - [Agregar etiqueta de datos].
- Para cambiar el eje de categorías: [Botón derecho] - [Seleccionar datos ]. La ventana que se obtiene es la siguiente.

- Hacemos clic en [Editar] ; hacemos clic en el cuadro que salga y seleccionamos en rango E16:E24 (límites superiores de todos los intervalos). Clic en [Aceptar] - Cambiemos el tamaño de la fuente de ambos ejes: Botón derecho en el eje X (en algún valor). - [Dar formato a eje] - [Fuente] En tamaño digitamos 7. Hacemos lo mismo en el eje Y.
- Para cambiar el ancho de cada barra y se parezca a un verdadero histograma: botón derecho en cualquier barra - [Dar formato a serie de datos] . La ventana que se obtenga debe ser similar a la que se muestra en la figura 2.15. En [Ancho del intervalo] corremos el botón a fin de obtener 0%. Hacemos clic en [Relleno] y dentro de ella hacemos clic en [Variar colores entre puntos]. Para una mejor presentación eliminamos las leyendas usando la tecla [Supr].
- Para modificar el título: Hacemos clic en el título actual digitamos Histograma de frecuencias.

- Si desea eliminar las líneas secundarias horizontales, hacemos en una de las líneas horizontales, luego [Supr]. Sólo debe quedar seleccionadas las líneas.
Ejemplo 04
Usando la tabla de frecuencias mencionado en el Ejemplo 03, construya histogramas para las frecuencias absoluta acumulada, relativa y relativa acumulada.
Procedimiento
Para la Frecuencia absoluta acumulada:
Seleccionamos el rango H16:H24. Usando el asistente para gráficos seleccionamos

Columna agrupada del tipo de gráfico [Columnas].
Pasando a la ficha [Series] haciendo clic en [Ró en el eje] seleccionamos el rango E16:E24. Continuando con el siguiente paso, ingresamos el título: “Histograma de la frecuenta absoluta acumulada”.
Luego de finalizar con el asistente, agregue las modificaciones que crea conveniente usando los últimos cuatro pasos del procedimiento dado en el Ejemplo 01.
Para la Frecuencia relativa o la frecuencia relativa acumulada
Seleccionamos el rango I16:I24 y construimos el gráfico siguiendo el mismo procedimiento anterior. Para la relativa acumulada, usamos J16:J24.
Nota:
Corrija el título del gráfico anterior haciendo clic con el botón derecho del ratón sobre el mismo.
Ejercicio 01
Construya un histograma para las frecuencias absolutas y relativas de la tabla dada en el archivo Sol Tabfrec.
Polígono de frecuencias
Si en un histograma de frecuencias se unen los puntos medios de cada una de las barras, se tiene un gráfico llamado polígono de frecuencias.
El polígono de frecuencias permite saber si los datos pueden ser ajustados a una distribución normal cuya gráfica es la campana de Gauss.
Ejemplo 05
Si en lugar de usar el tipo de gráfico Columnas en Ejemplo 03 usamos gráfico de líneas, obtendremos la gráfica que de la figura 2.17. (En MS Excel 2007).

Nota
Para lograr que el polígono empiece y termine en el eje X, extienda el rango de datos; es decir, digite 0 en G15 y en G25, aunque se borre el valor de n. Luego usando botón derecho en cualquier parte del gráfico, haga clic en [seleccionar datos] Use [editar] para ampliar el rango tanto de los datos como del Eje horizontal.
Gráfico de puntos
Este tipo de gráficos es usado fundamentalmente cuando el número de datos es pequeño y por tanto, no se requiere de una tabla de datos agrupados. Abra el archivo Graf 01 y siga las instrucciones para obtener un gráfico de puntos.
Ejercicio 02
Abra el archivo Graf 02 y grafique histogramas y/o polígonos siguiendo los procedimientos requeridos en cada caso; para ello es suficiente hacer clic en las barras de desplazamiento a fin de cambiar los datos para el gráfico.
Gráfico de columnas
El gráfico de columnas es el mismo que hemos usado para construir histograma de frecuencias.
El tipo de gráfico de columnas en Excel nos permite hasta 6 subtipos de gráficos:
La figura 2.18 muestra los diferentes subtipos de gráficos de columnas

Según el subtipo de gráfico de barras, podemos realizar comparaciones de series de datos por categorías así como comparaciones según su contribución en el conjunto, sea absoluta o porcentual.
Gráfico de barras
La única diferencia de este tipo de gráfico respecto a los gráficos de columna, es que en éstos las barras se muestran en forma horizontal.

Gráfico de líneas
Este tipo de gráfico nos permite conocer la tendencia o comportamiento lineal de los datos a través del tiempo.
El eje de categorías corresponde al tiempo y el eje vertical el valor de cada uno de los datos de la serie.
Ejercicio 03
Abra el archivo Graf02, vaya a la hoja Líneas para construir gráfico de líneas siguiendo haciendo uso de los botones de desplazamiento.
Gráfico circular
Un gráfico circular nos permite visualizar la contribución de cada valor de la serie de datos, en el conjunto. Sólo se puede graficar una sola variable o serie de datos.
Ejercicio 04
Abra el archivo Graf 02 para construir este tipo de gráficos según las indicaciones que allí se dan.
Gráfico de dispersión
El gráfico de dispersión nos permite comprender la relación que puede existir entre una serie de datos (Variable 1) y otra (Variable 2). Si existe relación, ésta puede ser lineal, cuadrática, exponencial, etc. Si así fuera, podremos decir que ambas variables están relacionadas entre sí en la cual, una depende de la otra.
Ejemplo 06
Abra el archivo Graf04.
a) Construiremos un gráfico de dispersión de la variable: Producción agrícola vs Volumen de fitosanitarios usando MS Excel 2003.
Para ello usaremos el siguiente procedimiento:
- Seleccionaremos el rango C13:C32.
- Hacemos clic en el icono del asistente para gráficos.
Seleccionamos el tipo de gráfico: XY(Dispersión). Elegimos el primer subtipo de diagrama. Hacemos clic en [Siguiente] - [Serie]. Haciendo clic en el cuadro de texto [Valores de x] seleccionamos el rango B13:B32. Luego [Siguiente] para después colocar el [T ítulo ], etc.
- Como opciones, después de graficar podemos reducir el tamaño de fuente y algunas otras opciones hasta obtener un gráfico similar al que se muestra en la figura 2.20.

b) ¿Podemos graficar la variable Producción agrícola, como dependiente del tiempo, lo que está dado en años?
En este caso graficaremos el rango B13:B32 en el Eje de valores y A13:A32 en el eje de valores.
La gráfica se muestra en la figura 2.21.
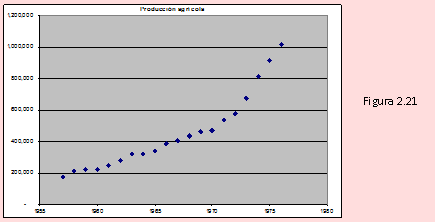
Esto nos dice que la serie de datos da la producción agrícola entre los años 1967 – 1976 ha sido creciente y se puede ajustar a un modelo lineal, aunque probablemente un modelo parabólico, podría ser un modelo más representativo o de mejor ajuste.
c) Usando los datos del Ejemplo 2, que se encuentra en la parte inferior de la misma hoja y a partir de la fila 52, determine cuál podría ser la variable dependiente y de quiénes dependería. Para ello construya gráficos de dispersión de pares de variables.
Ejercicio 05
Resuelva el ejemplo 06 anterior usando MS Excel 2007
Gráfico de tallos y hojas
Este tipo de gráfico es muy particular. Además de mostrar el valor de la mediana y la moda, muestra una forma de histograma con barras horizontales, determinado por la frecuencia de los datos no agrupados, nos permite recuperar los datos.
El gráfico consiste de un “tallo” determinado por los n-1 dígitos del valor del dato y un conjunto de “hojas” en el cual cada hoja está representada por el último dígito (dígito de las unidades) del valor del dato. Este dígito se repite de acuerdo al número de veces que se presenta el dato en la muestra.
Ejemplo 07
Supongamos por ejemplo que la muestra está formado por los siguientes datos: 18, 11, 09, 14, 12, 15, 17, 16, 11, 09, 14, 14, 12, 14, 09.
Como los datos contienen sólo dos dígitos, el tallo estará formado por el “0” o el “1”, mientras que las hojas estarán formadas por el dígito de las unidades. Para un mismo valor del tallo, la rama se expande a la derecha en un dígito, por cada nuevo dato que tenga el mismo valor.
La gráfica es la siguiente:
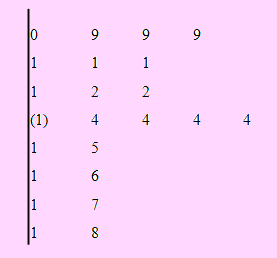
La mediana es el dato que ocupa la parte central de los datos. Su valor es 14.
Una manera de comprobarlo es ordenar primero los datos:
09 – 09 – 09 – 11 – 11 – 12 – 12 – 14 – 14 – 14 – 14 – 15 – 16 – 17 – 18
Aquí podemos observar que la mediana es 14.
Nota:
Hay otros gráficos que por el momento no lo explicaremos pues requieren de la presentación de otros temas. Al estudiar éstos, haremos uso de dichos gráficos, que nos ayudarán a comprender el tema, como es el caso del diagrama de cajas o el diagrama de dispersión, con mayor amplitud.
Siguiente sesión.