ESTADÍSICA DESCRIPTIVA

2.1 Concepto de Estadística.
2.2 Variables cualitativas y cuantitativas.
2.3 Muestreo: Conceptos.
2.4 Problemas que debe resolver un investigador.
2.5 Tipos de muestreo.
2.6 Tabla de distribución de frecuencias.
2.7 Análisis exploratorio de datos (EDA).
2.8 Estadístico de la muestra.
2.9 Medidas de tendencia central y de posición.
2.10 Medidas de dispersión.
2.11 Asimetría.
2.12 Problemas propuestos.

2.1 CONCEPTO DE ESTADÍSTICA

Desde un punto de vista práctico la Estadística es el conjunto de métodos, técnicas, procedimientos o herramientas que nos permiten obtener uno o más indicadores con los cuales podemos realizar diversos tipos de análisis de datos.

Los datos contienen mucha información. Los investigadores y estadísticos siempre le están extrayendo toda o parte de la información contenida en los datos. Dependiendo de cómo se les trata y qué es lo que queremos de ellos (los datos), podemos darle también diferentes tipos de interpretación.

Las ventas de tres tipos de aceite para vehículos en una estación de servicio, durante una semana, pueden proporcionarnos mucha información:

-    Podemos estar interesados en comparar las ventas diarias entre los tres tipos de aceites.
-    Podemos estar interesados en analizar el comportamiento de las ventas durante la semana.
-    Podemos preguntarnos el día de mínima o máxima venta por cada tipo de aceite.
-    Podemos comparar las días de máxima o mínima venta por aceite.
-    Podemos obtener el monto total de la venta de aceite en toda la semana.
-    Podemos estar interesados en averiguar el promedio diario de venta.
-    Podemos tratar de saber cómo varía las ventas diariamente por aceite.
-    Podemos preguntarnos cómo serán las ventas para la próxima semana, el promedio; su variabilidad; si la máxima o mínima venta volverá a producirse el mismo día; si disminuirá el monto de las ventas respecto a esta semana.
-    Podemos proyectar nuestras ventas para todo el mes
-    Podemos construir un programa de suministro de aceite
-    Podemos incrementar o reducir nuestras provisiones semanales de aceite.
-    Etc.

Todas estas inquietudes pueden ser resueltas mediante la aplicación de los instrumentos de medición de la Estadística.

La naturaleza de estas herramientas o instrumentos de medición nos permiten dividir a la Estadística en

Estadística Descriptiva
Estadística Inferencial

La primera se encarga del análisis de los datos y la generación de diversos tipos de indicadores. Puesto que su estudio se realiza sobre una parte de la población: Muestra, los resultados de sus estudios describen el comportamiento de la muestra.

La segunda utiliza estos indicadores para realizar procesos de estimación sobre el comportamiento poblacional. Las herramientas de la Estadística Inferencial nos permiten comprobar supuestos o hipótesis formuladas al empezar el estudio.

Como veremos en los siguientes capítulos, el programa MS Excel dispone de diversas funciones y herramientas para apoyar al investigador en el análisis de los datos en sus diferentes variantes, sea con el Análisis Exploratorio de Datos (EDA), en la obtención de los Estadísticos (indicadores) de la muestra; en la utilización de éstos como estimadores de los parámetros poblacionales o como test para probar la validez o falsedad de ciertas afirmaciones respecto al comportamiento de la población objetivo.

2.2 VARIABLES CUALITATIVAS Y CUANTITATIVAS

La forma de representar a un conjunto de datos, que son los valores obtenidos al estudiar una determinada característica de la población, sujeta a estudio, es mediante el uso de las variables,

Cuando hablamos de datos debemos tomar en cuenta si estos califican o cuantifican una determinada característica de la población sujeta a estudio.

Por ello diremos que una Variable Cualitativa califica, agrupa o identifica a una variable.

Una variable cualitativa puede ser a su vez:

-    Cualitativa nominal: Cuando nomina, identifica con un valor, al elemento de la población o muestra. Si el interés es analizar el comportamiento de un conjunto de electores peruanos, el DNI es un dato que identifica o nomina a un elector. El número de transacción, en una operación bancaria identifica a la operación. El género, estado civil, color o marca de un vehículo constituyen variables cualitativas nominales.

-    Cualitativa ordinal: Cuando agrupa o clasifica varios valores de la variable en grupos con cierta afinidad o característica. De un conjunto de electores, su nivel socioeconómico, su grado de instrucción, el número de mesa donde votan son variables cualitativas ordinales.

Una Variable Cuantitativa cuantifica a los elementos de la población o muestra. Por ejemplo el ingreso mensual de un trabajador; el peso de un melón; el número de clientes de un banco que esperan ser atendidos en una ventanilla; el número de vehículos esperando en una caseta de control de peaje; el tiempo que tarda un operador de la caseta en atender a un cliente; etc.

De los ejemplos dados de variable cuantitativa, podemos deducir que hay dos tipos de variables cuantitativas: Aquellas que se producen por lo general de un conteo: Número de clientes que esperan ser atendidos y aquéllas otras como el tiempo que el operador se tarda en atender a un cliente. Los primeros constituyen variables discretas y los segundos, variables continuas.

Las variables discretas se pueden enumerar: x₁, x₂, …, x_k, …, xn.
Las variables continuas no se pueden enumerar, se representa por intervalos: a  x  b.

Finalmente diremos que cualquiera que sea el elemento de la población, puede ser representada por una variable.


2.3.    MUESTREO: CONCEPTOS

Una población es el conjunto de elementos que gozan de algunas características o propiedades comunes, las que permiten identificarlos y definir su comportamiento. El propósito del investigador o quien realiza un análisis de los datos, es estudiar el comportamiento de la población.
Este estudio se realiza aislando alguna de sus características, objeto del muestreo, la que se puede representar mediante una variable. De esta manera podemos crear modelos matemáticos para dicha variable.

He aquí algunos ejemplos:

Si se trata de saber cómo se comportarán los electores respecto a un cierto candidatos; si se pretende comparar los ingresos promedios de los trabajadores de dos cadenas de tiendas; si se pretende estudiar cómo variará las ventas de un determinado producto en cada temporada, debemos estudiar el comportamiento de todos los elementos sujetos a estudio: la población electoral, los trabajadores de las dos cadenas de tiendas, la venta de los productos por temporada; etc.
La solución a todas estas inquietudes implicaría realizar un censo poblacional cada vez que se quiera conocer el comportamiento poblacional. Si se quisiera resultados mensuales, pues el censo se haría mensualmente.

Pero realizar un censo tiene serios inconvenientes:

-    El costo del estudio
-    El tiempo requerido para obtener los datos para el análisis
-    Oportunidad

Por ello es que el estudio se realiza sobre una parte de la población a la cual se le denomina una muestra. Una muestra es un subconjunto de la población. Esta muestra tiene que ser representativa; de otra manera el estudio daría resultados sesgados.

El proceso de extraer los elementos de la población para obtener la muestra se conoce como Muestreo.

El muestreo puede ser probabilístico, cuando cada elemento de la población tiene las mismas probabilidades de ser seleccionado; es decir, si la población tiene N elementos, la probabilidad de que un elemento cualquiera sea elegido será 1/N. El muestreo no probabilístico, cuando la selección se realiza tomando en cuenta ciertos criterios que pueden ser incluso subjetivos.

Ejemplo de características de una población representada mediante la definición de una variable:

1.    Los ingresos mensuales de Todos los trabajadores de la PEA.
2.    Los ingresos mensuales de los trabajadores del Sector Textil.
3.    Los ingresos mensuales de todos los trabajadores de Construcción Civil del Perú.
4.    Si sólo quisiéramos estudiar el comportamiento de los trabajadores de Construcción Civil de Lima, podríamos tomar como la población a los ingresos mensuales de los trabajadores del Sector de Construcción Civil, de Lima Metropolitana  como población.
5.    El número de horas de estudio adicionales que tiene cada uno de los alumnos de la Universidad de Lima.
6.    El tiempo de vida de las bacterias contenidas en una determinada sustancia.
7.    El rendimiento académico de los alumnos de los colegios secundarios de Lima Metropolitana.
8.    Las tendencias electorales de la población de una región del Perú, agrupadas por los sectores de la PEA.
9.    Niveles de preferencia de la población del Perú por los últimos modelos de Ferrari.
10.    El número de viajes semanales que realiza una persona por la Avenida Túpac Amaru.
etc.

Ejemplos de reconocimiento

Primer caso:

El gerente de marketing de Bell S.A. está interesado en estimar las ventas promedio por día de dos de sus productos estrella de uso personal. Para ello desea realizar un muestreo de la facturación de ventas, seleccionando aleatoriamente 36 facturas de las últimas 5 semanas. El gerente está interesado también en estimar la proporción de clientes que consumen sus dos productos tanto hombres como mujeres así como la preferencia por el color, la forma y contenido (en ml) de cada envase.

Tomando en cuenta este enunciado, determine:

a) La población objetivo.
b) La muestra y su tamaño.
c) Defina e indique el tipo de cada una de las variables de interés.
d) Defina los parámetros de interés a ser estimados.
e) Defina los estadísticos de interés que se obtendrán en la muestra.

Solución

a) Si la población objetivo es el conjunto está formado por todos los elementos sujetos a estudio, entonces, el conjunto de todas las facturas emitidas por la venta de estos dos productos en las últimas cinco semanas, constituirán la población objetivo.
b) La muestra está formada por las 36 facturas seleccionadas aleatoriamente.
c) Primera variable: Monto de las ventas por cada producto en cada factura. Es una variable cuantitativa continua.
Segunda variable: Porcentaje de cada producto comprados por hombres y mujeres.
Tercera variable: Número de hombres y mujeres que prefieren cada producto
Otras variables: Porcentaje de hombres y mujeres que prefieren estos productos por el color, envase y contenido
d) Los parámetros a ser estimados son: Monto promedio por producto, proporción de productos comprados según género, color, tipo envase y contenido del envase.
e) Los parámetros a ser estimados son: Monto promedio por producto, proporción de productos comprados según género, color, tipo envase y contenido del envase en la muestra de 36 facturas seleccionadas.

Segundo caso

Milward Brown desea investigar acerca de la situación laboral de los estudiantes universitarios egresados en la década de los 90’s, de las especialidades de Ingeniería y administración, de las diversas universidades del País. Con este fin se selecciona una muestra aleatoria de 250 estudiantes. Se tomó información con respecto a las siguientes características: Situación laboral (Empleado, desempleado, sub-empleado); departamento en el cual reside; ingreso mensual (en soles); número de empleos que tuvo; estado civil en la actualidad.

Defina Usted los siguiente conceptos, para esta este caso: Población, muestra, variables y tipo de variables, seleccione dos variables y defina para esta un posible parámetro y su respectivo estadígrafo

Solución

Población: Todos los estudiantes egresados universitarios de las facultades de Ingeniería y Administración en la década de los 90’s. Muestra: Los 250 estudiantes egresados seleccionados aleatoriamente.
Variables(Por facultad):
         Situación laboral: Cualitativa, nominal
         Departamento de residencia: Cualitativa, nominal
         Ingreso mensual: Cuantitativa, continua
         Número de empleos que ha tenido: Cuantitativa, discreta
         Estado civil: Cualitativa, nominal
Situación laboral (Por facultad):
Parámetro: Proporción (o porcentaje) de egresados según su situación laboral.
Estadístico: Proporción de egresados según su situación laboral en la muestra
Ingreso mensual:
Parámetro: Ingreso mensual promedio de cada egresado
Estadístico: Ingreso mensual promedio de cada egresado en la muestra.

Formulario de ingreso de datos

Diseñar y codificar un formulario que permita ingresar los datos del segundo caso hacia una hoja del Excel.

Solución

Nombre del formulario: FrmPanel Nombre del módulo: ModPanel (usado para activar el panel) Elementos en el formulario: La siguiente imagen el contenido del formulario:

Hemos insertado:

Cuatro cuadros de texto: TxtCodigo, TxtNombre, TxtIngreso y TxtNroEmp
Tres cuadros combinado: CboSit, CboDpto, CboECivil.
Cuatro botones de comando: CmdLoad que carga la tabla; CmdNuevo que permite limpiar el panel para ingrear nuevos datos, CmdFin para grabar y dar por terminado el uso del formulario.

El siguiente es el código del módulo:

Sub PanelDatos()
fName = Application.GetOpenFilename
Workbooks.Open fName
FrmPanel.Show
End Sub

Como se puede apreciar, se ubica el nombre del archivo hacia el cual se ingresarán los datos, se abre y luego se invoca el formulario llamado FrmPanel.
El siguiente es el código contenido en el formulario:

Dim iX As Integer

Private Sub CmdAceptar_Click()
iX = iX + 1
Cells(iX, 1) = TxtCodigo
Cells(iX, 2) = TxtNombre.Text
Cells(iX, 3) = CboSit.List(CboSit.ListIndex)
Cells(iX, 4) = CboDpto.List(CboDpto.ListIndex)
Cells(iX, 5) = Val(TxtIngreso.Text)
Cells(iX, 6) = Val(TxtNroemp.Text)
Cells(iX, 7) = CboECivil.List(CboECivil.ListIndex)
Cells(1, 10) = iX

End Sub

Private Sub CmdFin_Click()
' ActiveWorkbook.Save
End

End Sub

Private Sub CmdLoad_Click()
CboSit.AddItem "Empleado"
CboSit.AddItem "Sub empleado"
CboSit.AddItem "Desmpleado"

CboECivil.AddItem "Soltero"
CboECivil.AddItem "Casado"
CboECivil.AddItem "Divorciado"
CboECivil.AddItem "Separado"
CboECivil.AddItem "Viudo"

CboDpto.AddItem "Amazonas"
CboDpto.AddItem "Ancash"[br>
CboDpto.AddItem "Apurimac"
CboDpto.AddItem "Arequipa"
CboDpto.AddItem "Ayacucho"
CboDpto.AddItem "Cajamarca"
CboDpto.AddItem "Callao"
CboDpto.AddItem "Cuzco"
CboDpto.AddItem "Huancavelica"
CboDpto.AddItem "Huánuco"
CboDpto.AddItem "Ica"
CboDpto.AddItem "Junin"
CboDpto.AddItem "La Libertad"
CboDpto.AddItem "Lambayeque"
CboDpto.AddItem "Lima"
CboDpto.AddItem "Loreto"
CboDpto.AddItem "Madre de Dios"
CboDpto.AddItem "Moquegua"
CboDpto.AddItem "Pasco"
CboDpto.AddItem "Piura"
CboDpto.AddItem "Puno"
CboDpto.AddItem "San Martin"
CboDpto.AddItem "Tacna"
CboDpto.AddItem "Tumbes"
CboDpto.AddItem "Ucayali"

Hoja = Trim(InputBox("Nombre de la hoja si es nueva", , "Datos"))
If Hoja = "Datos" Then
Sheets(Hoja).Select
Else
Sheets.Add
ActiveSheet.Name = Hoja
Cells(1, 10) = 1
End If

iX = Cells(1, 10)
TxtCodigo.SetFocus
End Sub

Private Sub CmdNuevo_Click()
On Error Resume Next
TxtCodigo.Text = ""
TxtNombre.Text = ""
TxtIngreso.Text = ""
TxtNroemp.Text = ""
TxtCodigo.SetFocus

End Sub

El archivo Ej de formulario contiene el código completo.

2.4 PROBLEMAS QUE DEBE RESOLVER EL INVESTIGADOR

Llamaremos investigador a toda persona que está interesado en conocer el comportamiento de una población y que para ello debe realizar un proceso de muestreo.
Este investigador debe resolver dos grandes problemas (además de estos dos: el diseño de la encuesta, su contenido, la forma de presentar las preguntas, etc.):
- Cuál es el número de elementos que deben conformar la muestra
- Cómo seleccionar los elementos que deben conformar la muestra

Tamaño de muestra
En el capítulo sobre Estimación de parámetros se darán las fórmulas para estimar el tamaño de muestra, tanto para estimar la media como para estimar la proporción.
Aquí supondremos que el tamaño de muestra ya se conoce y es n.

2.5 TIPOS DE MUESTREO PROBABILISTICO

Si lo que deseamos es seleccionar n elementos de la población sujeto a estudio, debemos contemplar ahora, cómo seleccionar estos elementos. Los siguientes son los tipos de muestreo más utilizados.

- Muestreo Aleatorio Simple (MAS)
- Muestreo Sistemático (MS)
- Muestreo Estratificado
- Muestreo por Conglomerados.
- Otros tipos de muestreo como el Muestreo Multietápico.

En Excel se dispone de la herramienta Análisis de datos para generar un conjunto de valores que pueden representar los números de elementos de la población a ser seleccionados para formar la muestra. En cuanto a muestreo el Excel permite extraer una muestra usando el muestreo aleatorio simple y el sistemático.

Muestreo Aleatorio Simple

Se basa en seleccionar los elementos de la población de manera aleatoria, al azar. El supuesto para este tipo de muestreo es que cada uno de los elementos de la población tiene igual probabilidad de ser seleccionados. Esto es, si Xi representa a un elemento de la población, p(X = Xi ) =1/N es la probabilidad de que dicho elemento sea elegido para conformar la muestra.

Para llevar a cabo este tipo de muestreo se requiere de una lista o tabla de números aleatorios y la lista de los elementos de la población.

Procedimiento en Excel:

Abra el archivo Bancordia. En la hoja Estadísticas se dispone de los saldos en cuenta corriente de 2074 clientes del Banco La Concordia. En la hoja Muestra aleatoria, obtenga una muestra de tamaño 320.

Al usar la secuencia [Datos] - [An álisis de datos], se obtendrá la ventana de diálogo de la izquierda de la figura 2.1. La imagen de la izquierda corresponde a la secuencia que se debe seguir para usar la herramienta [Muestra] usando Ms Excel 2003. En este caso es: [Herramientas] - [An álisis de datos].



En Ms Excel 2007, Ms Excel 2010 y Ms Excel 2013, debe usar la siguiente secuencia:
Al hacer clic en [Análisis de datos] se obtiene la ventana mostrada en la figura 2.2. Haga clic en [Aceptar]



El rango de la columna que contiene los saldos se llama Saldos. Este rango de datos contiene rótulo en la primera fila. Se extraerá una muestra de tamaño 320. La muestra se obtendrá en una nueva hoja llamada Muestra aleatoria, a partir de la celda A1.

Observe que en esta ventana hemos activado el botón [aleatorio] para usar el muestreo aleatorio simple.

Recuerde que el rango de datos puede estar en cualquier hoja. Recuerde también que si hubiera más de una hoja conteniendo un rango con el mismo nombre, para hacer referencia a uno de ellos en particular, el nombre de rango Saldos, debe estar precedido por NombreHoja!.

Muestreo Sistemático

El muestreo sistemático se basa en la selección de los elementos de la población usando una serie de progresión aritmética.
Sea N el tamaño de la población sujeta a estudio. Supongamos que se desea obtener una muestra de tamaño n. Si se define como la semilla, entonces los elementos que conformarán la muestra serán:

a, a + k, a + 2k, a + 3k,…, a + (n-1)k
donde a recibe el nombre de arranque aleatorio.

Procedimiento en Excel:

Usemos los datos de la hoja Estadística del archivo Bancordia.
El valor de la semilla la encontramos usando k = N / n donde

N = Contar(Saldos); n = 320

En Excel 2003: Use la secuencia: [Herramientas] - [Análisis de datos] - [Muestra]-[Aceptar]. En Excel 2007: [Datos] - [Análisis de datos] - [Muestra]
Complete la ventana según se muestra en la siguiente figura.



Grabe el archivo como Muestras de Bancordia.xls.

Muestreo estratificado



El muestreo estratificado consiste en dividir a la población en un conjunto de partes cada una de las cuales recibe el nombre de estrato, de tal manera que los elementos que la conforman posean ciertas características o propiedades afines, las que por supuesto no las poseen los otros estratos.

Entonces, para seleccionar una muestra basado en este tipo de muestreo se debe dividir a la población de tamaño N, en estratos, de tamaño N_j, cada uno. Al interior de cada uno de los estratos, se elige una submuestra de tamaño nj. Para elegir estos elementos sí se puede usar el muestreo aleatorio simple.

Si p_j = N_j/N define la proporción de elementos en el j-ésimo estrato, y n es el tamaño de la muestra, entonces n_j = n*p_j será el número de elementos que se seleccionen del estrato j para formar la jésima submuestra. De manera que si la población se divide en k estratos

n₁ es el tamaño de la sub muestra en el Estrato 1
n₂ es el tamaño de la sub muestra en el Estrato 2
.... n_k es el tamaño de lasub muestra en el Estrato k,

Con lo cual n = n₁ + n₂+... + n_k será el tamaño de muestra general.

Ejemplo: Escriba una macro para obtener una muestra estratificada

Solución

Los datos necesarios para obtener los nj elementos de cada estrato son los siguientes:
Tamaño de la población: N
Tamaño de cada estrato: Nj o en todo caso, la proporción de cada estrato: p_j.
El archivo Muestreo por estratos contiene la forma de ingreso de los datos. Haga clic en el botón de cuadro combinado que aparece en la celda C7 para seleccionar el número de estratos con los cuales debe trabajar y luego debe responder a las peticiones de tamaño de población, de muestra y finalmente debe indicar si lo que se dispone de datos son los tamaños de cada estrato o las proporciones de ellos (esto dado en porcentaje).

El código se muestra en el siguiente procedimiento:

Sub MuestxEst()
Sheets("Estrat").Select
Range("C11:G50").Clear
Cells(4, 3) = Val(InputBox("Tamaño de la población: "))
Cells(5, 3) = Val(InputBox("Tamaño de la muestra: "))
iX = Val(InputBox("Digite 0 si vas a ingresar tamaño de estrato" + Chr(13) + _
"Digita 1 si vas a ingresar como dato las proporciones de cada estrato en %"))
nStrat = Cells(7, 3)
For i = 1 To nStrat + 1
Cells(i + 10, 3) = "Estrato " + Trim(Str(i))
Cells(i + 10, 4).Borders.LineStyle = xlSingle
Cells(i + 10, 5).Borders.LineStyle = xlSingle
Cells(i + 10, 7).Borders.LineStyle = xlSingle
Next
Suma = 0
For i = 1 To nStrat + 1
If iX = 0 Then
Cells(i + 10, 7) = "=Int(RC[-3]/R4C3*R5C3+0.5)"
Else
Cells(i + 10, 7) = "=Int(RC[-2]*R5C3/100 + 0.5)"
End If
Next
Cells(7, 3) = ""
End Sub


Muestreo por conglomerados

Sin embargo estas tres formas de estudiar a la población, a través de la selección de una muestra, no son los únicos. En muchos casos cuando se trata de consultar a una familia, a una célula de producción, a un lote de cajones de naranja, una sección de un colegio de cinco mil alumnos, etc., se recoge la información de esta familia, de esta célula, de ese cajón, de esa sección; es decir, a cada uno de ellos se les define como una unidad, como un elemento de la población.
Veamos algunos casos:

i) Un determinado laboratorio de perfumería desea conocer la preferencia de sus productos en cada familia de un determinado distrito.
ii) El departamento de investigación del Instituto de Estadística desea conocer el promedio de los ingresos por familia de los distritos de menores recursos.
iii) Un vendedor de frutas desea conocer el promedio y el total de frutas calificadas como de calidad superior, de cada una de las variedades que comercializa.
iv) Una cadena de hoteles está interesado en conocer el número promedio de charlas de actualización técnico-profesional que debe impartir a sus empleados en cada una de sus 30 sucursales del Perú.

En el primer ejemplo no interesa la preferencia de la familia, nos interesa la preferencia de cada uno de los integrantes de la familia. Puede ser que la madre prefiera una colonia suave, y las hijas una del mismo tipo, pero fuerte; definitivamente la preferencia de los varones no puede ser mezclada con el de las mujeres en la familia. En el caso del ejemplo iv), teniendo en cada sección diversas categorías de empleados, se supone que la capacitación deberá tomarlo en cuenta; mal podríamos hacer si la charla es la misma para todos. Aquí también interesa la opinión de los miembros de cada sección y la opinión de la sección como unidad.

Por estas razones el tipo de muestreo que se acostumbra a elegir en estos casos constituye unmuestreo por conglomerados.

Nota resumen

En el Muestreo estratificado: Debe existir homogeneidad dentro del estrato y heterogeneidad entre los estratos. En el muestreo por conglomerados: Debe existir heterogeneidad dentro de los conglomerados y homogeneidad entre los conglomerados.

Y en general, en todos los casos del muestreo probabilístico se deberá observar que la muestra sea representativa de la población.

Ejercicio de complementación

Intente diseñar un procedimiento y luego codifíquelo en VBA a fin de crear una macro que permita automatizar de alguna manera el muestreo por conglomerados.

2.6 TABLA DE DISTRIBUCIÓN DE FRECUENCIAS

Una vez que se ha obtenido la muestra, el investigador puede realizar dos tipos de acción, primordialmente:

- Organizar sus datos para una adecuada presentación
- Realizar un Análisis Exploratorio de Datos (EDA)

Los datos “tienen mucha información”; tienen mucho que decirle al investigador. Éste debe ser capaz de usar la herramienta estadística adecuada para interpretar lo que los datos quieren decirle.

Respecto a la primera acción, el investigador puede presentar los datos en forma tabular, a los cuales se les conoce como “Tablas de distribución de frecuencias”.

En el caso de la segunda acción, existen muchas herramientas gráficas a los cuales se puede someter los datos. El tratamiento gráfico de los datos es una herramienta muy poderosa que, como veremos, nos permite conocer el comportamiento de la muestra y con ello de la población y estimar y/o predecir el comportamiento futuro de la población sujeta a estudio.
En esta sección haremos uso del Excel para construir tablas de distribución de frecuencias. Usaremos las funciones y herramientas que ella tiene y codificaremos otras mediante el uso de macros.

Supongamos que X₁, X₂, X₃,…, Xn es una muestra de tamaño n, extraída de una población sujeta a estudio.

Supongamos también que esta muestra es una muestra aleatoria; es decir, que la muestra está formada por un conjunto de variables aleatorias independientes y que la selección de cada una de ellas tiene igual probabilidad de ser seleccionada.

La siguiente imagen muestra la estructura de una tabla de distribución de frecuencias.

Donde       LimInf_i           : Límite inferior de la i – ésima clase o intervalo

                        LimSup_{i             :} Límite superior de la i – ésima clase o intervalo

                        X_i                    : Marca de clase del i - ésimo intervalo

                        f_i                     : Frecuencia absoluta de la clase o intervalo i.

                        F_i                     : Frecuencia absoluta acumulada del intervalo i.

                        h_i                     : Frecuencia relativa de la clase o intervalo i

                        H_i                    : Frecuencia relativa acumulada del intervalo i

Cálculo de la marca de clase o punto medio de cada intervalo:.



Procedimiento para construir una tabla de frecuencias en Excel 2007

El procedimiento lo daremos mediante la solución de los siguientes dos ejemplos.

Ejemplo 01

Construir una tabla de frecuencias para los saldos (en soles) en cuenta corriente de los clientes del Banco Bancordia contenidos en el archivo Bancordia
Grabe el archivo como SolBancordia.xls

Solución

Como se puede comprobar, en la primera hoja hay 2074 clientes. Vamos a extraer una muestra aleatoria de 320 cuentas y trabajaremos con ella. Seleccione el rango B9:B2083 y asígnele por nombre el contenido de la primera fila: Saldos.

Usando la secuencia: [Datos] - [An álisis de datos] - [Muestra] - [Aceptar] y completando la siguiente ventana como se muestra en la figura 2.5.



No espere obtener los mismos datos que aquí mostramos. Es aleatorio. Inserte una fila al inicio y ponga como nombre de columna Saldos.Seleccione el rango A2:A351 y póngale por nombre MuestraSaldos.

Obtenga primero las siguientes estadísticas usando las funciones adecuadas, según


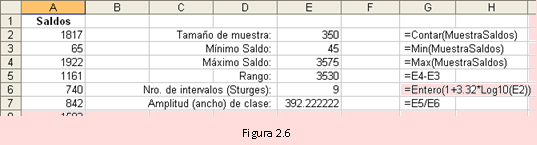
se muestran en la figura 2.6. A la derecha se muestra las fórmulas que se debe usar.
Diseñe una tabla como se muestra en la figura 2.7. Podría hacerlo a partir de C14.



A continuación vamos a calcular los límites inferior y superior de cada clase.

Primer intervalo (clase):        Lim. Inf:             =E3     Mínimo dato.

                                               Lim. Sup:        =D16+E7
Segundo intervalo                   Lim. Inf:         =E16

                                               Lim. Sup:        =D17+$E$7



Copiando las fórmulas de D17:E17 para los otros intervalos, obtendrá los demás intervalos.

Cálculo de la marca de clase o punto medio (Xi)

En F16, digite: =(D16+E16)/2
Copie ahora para los otros intervalos.

Cálculo de la Frecuencia absoluta (fi):

Para ello usaremos la función:

=Frecuencia(RangoDeDatos,ColumnaGrupos)

Donde
RangoDeDatos: Contiene todos los elementos que conforman la muestra
ColumnaGrupos : Es el rango de los límites superiores de los intervalos

Como esta función implica el uso de operaciones con argumentos: - Seleccionamos primero todo el rango de salida: G16:G24 - Luego ingresamos la función: =Frecuencia(Saldos,E16:E24) - Usamos la combinación: [CTRL]+[SHIFT]+[ENTER].

En la celda G25 sume el rango G16:G24 para comprobar que n = 350.

Cálculo de la frecuencia absoluta acumulada (F_i):

En H16 ingresamos: =G16
En H17 ingresamos: =H16+G17
Luego copiamos esta última fórmula para los otros intervalos.
Compruebe que la última frecuencia acumulada coincida con el valor de n.

Cálculo de la frecuencia relativa (hi):

En I16 ingresamos: =G16/$G$25 (La fijamos para que no cambie al copiar).
Copiamos esta fórmula para los otros intervalos.

Cálculo de la frecuencia relativa acumulada(Hi):

En J16 ingresamos: =I16
En J17 ingresamos: =J16+I17

Luego copiamos esta última fórmula para los otros intervalos.
Compruebe que la última frecuencia acumulada coincida con el valor de 1.
La siguiente figura 2.9, muestra los resultados que se deben obtener.



Observación:

Los resultados que obtenga es probable que no sean iguales con los que aquí se muestran pues son dos muestras diferentes.

Interpretación de la tabla de frecuencias (Usaré estos resultados)

Decíamos que los datos pueden proporcionarnos mucha información. Analicemos la tabla encontrada.

- El mínimo saldo en cuenta corriente de los clientes del banco es 114 mil soles
- El máximo saldo es de 3’575 mil soles
- El banco tiene 25 clientes (f1) cuyos saldos están entre 114 y 498.56 mil soles.
- Los mayores saldos pertenecen a 26 clientes (f9), y varían entre 3190.44 y 3575.00.
- El 5% de clientes del banco tienen saldos entre 498.56 y 883.11 (h2).
- Los mayores saldos en cuenta corriente del banco representan el 7% (h9).
- El banco tiene 41 clientes con saldos menores que 883.11 mil soles (F2).
- El banco tiene 217 clientes cuyos saldos van desde 114.00 hasta 2036.78 (F5).
- El banco tiene 51 clientes con saldos superiores a 2805.89 (F9 – F7)
- El 12% de los clientes del banco tienen saldos inferiores a 883.11 mil soles.

Ejemplo 02

Los montos de las ventas mensuales de latas de conserva de anchoveta vendidos en un mes, se dan en la siguiente tabla (Soles):



Se pide:

a)Construir una tabla de distribución de frecuencias para los montos de las ventas de conservas en Trujillo. Use la fórmula de Sturges para obtener el número de intervalos.

b)Complete la tabla de frecuencias de los montos de venta en Lima, dado en la figura 2.10.



Solución

a) Copiamos todos los datos hacia una hoja vacía en un libro nuevo (Sugerencia: En lugar de digitar todos los datos, podemos abrir el archivo Tabla03.doc; seleccionar los datos de Trujillo, incluyendo su nombre y pegarlo a partir de la celda A1 de la hoja1 del libro nuevo.

Seleccionamos todo el rango y le damos nombre VTruji. El número de datos lo obtenemos usando =Contar(VTruji); esto es, 80. Usando Sturges tenemos: =1.32*Log10(n), redondeando al entero inmediato obtenemos el número de intervalos.

De acuerdo al procedimiento indicado en el Ejemplo 01, construiremos unatabla de frecuencias.



Obtendremos las estadísticas dadas en la figura 2.5

Siguiendo con dicho procedimiento, obtendremos la tabla. El resultado debe ser el que se muestra en la figura 2.11

Nota:

La solución a este ejemplo se encuentra en el archivo Sol tabfrec01.

b) A continuación daremos solución a esta pregunta:

- Cálculo de los límites de los intervalos: Amplitud (a) = X₂ – X₁ = 2850.14
- Como Lim. Sup. del 1er. Intervalo es: Li1 + a = 14422.07 entonces hallamos Li1 = 12997.00. A partir de este valor hallamos todos los otros.
- Teniendo los intervalos calculamos las marcas de clase restantes.
- F1 = f1 = 12 (dato). f2 = 23 – F1; F3 = 80*h6 = 33 ; f4 = 80*h4
- F7 = 80 F6= 80*H6 = 69 f7 = F7 – F6 f6 = 80*h6 F5 = F6 – f6
- f3 = F3 – F2 F4 = F3 + f4 f5 = F5 – F4
- A partir de la columna de las frecuencias absolutas se puede calcular las otras.

Nota:

La solución a este ejemplo se encuentra en el libro Sol tabfrec01.

Observación importante:

El siguiente archivo puede ayudarle mucho si desea obtener una tabla de frecuencia, aunque también genera otros resultados no contemplados aún. El archivo se llama Generador 2010 II.
Siguiente sesión.