En esta oportunidad vamos a realizar cálculos con matrices como la suma, el producto, determinante de una matriz y la inversión de matrices, además de leer la o las matrices e imprimir la matriz resultado.
Como lo explicábamos en la sección anterior, la solución de un problema casi siempre tiene segmentos en los que en control de la ejecución de acciones se realiza independiente de otras acciones. Por ejemplo, mientras se está leyendo los datos para una matriz de 10 por 10, la Sección de cálculo y la de impresión de los resultados no está siendo ejecutado; está en espera. Por otro lado, sólo cuando se ha terminado de leer los datos es que se realizará los cálculos; y sólo cuando se ha obtenido los resultados se podrá imprimir los resultados, aunque los datos ya se pueden imprimir pero después de haber sido leídos
Por otro lado, para que el segmento de cálculo o el de impresión se ejecuten, deben recibir datos del segmento de lectura.
De manera que, para resolver el problema expuesto en el segundo párrafo, vamos a escribir un procedimiento de lectura de matrices; uno que permita sumar matrices, otros que multiplique, que invierta, que obtenga el determinante de una matriz y finalmente otro que permita imprimir la matriz resultado.
Todos estos procedimientos deben ser llamados desde uno principal.
Antes de pasar al detalle, abra su libro MisMacros.xlsm o haga clic aquí
Vaya al editor e inserte un nuevo módulo. En la ventana de propiedades (lado inferior izquierdo), haga clic en la propiedad
En el lado derecho digite el siguiente procedimiento principal:
Sub CalcMatricial()
Dim A(20, 20), B(20, 20), C(20, 20), d As Double
Dim m, n, k As Integer
xKey = Val(InputBox("Qué operación desea hacer?" + Chr(13) + "1 = Sumar" + Chr(13) + "2 = Multiplicar" + Chr(13) + "3. Determinante" _ + Chr(13) + "4. Matriz inversa"))
Select Case xKey
Case 1:
Call LectMatrices(nA, mA, A)
Call LectMatrices(nB, mB, B)
Call MatrSuma(nA, mA, A, B, C)
xTexto = "La matriz suma es: "
Call SalidaMatriz(nA, mA, C)
Case 2:
Call LectMatrices(nA, mA, A)
Call LectMatrices(nB, mB, B)
Call MatrProd(nA, mA, mB, A, B, C)
xTexto = "La matriz producto es: "
Call SalidaMatriz(nA, mB, C)
Case 3:
Call LectMatrices(nA, mA, A)
Call MatrDeterm(nA, A, C, d)
MsgBox "El determinante de la matriz es: " + Str(d)
Case 4:
Call LectMatrices(nA, mA, A)
Call MatrInversa(nA, A, C, d)
xTexto = "La matriz inversa es: "
Call SalidaMatriz(nA, nA, C)
End Select
End Sub
Explicación:
Primero hemos declarado las matrices que vamos a usar así como los números enteros que nos van a servir como subindices para hacer referencia a los elementos de cada matriz.
De una manera elegante (tenga cuidado al digitar), se pide ingresar el tipo de operación que se va a realizar.
Con la sentencia Select Case, determinamos las acciones que se debe realizar según al número (xKey) que se digitó: Si es suma(1), se llama a LectMatrices, recibiendo el orden nA*mA de la primera matriz; se llama a MatrSuma pero se le envía el orden de las dos matrices (que tienen que ser del mismo orden), se le pasa la matriz A y B y el procedimiento devolverá la matriz C que contiene la suma. Finalmente se llama al procedimiento SalidaMatriz.
Siguiendo el mismo procedimiento se han digitado las instrucciones con el producto (que debe cumplir con las reglas de multiplicación) y las otras operaciones.
Estos son los procedimientos:
La lectura de matrices:
Sub LectMatrices(n, m, A)
n = Val(InputBox("Nro de filas: "))
m = Val(InputBox("Nro de columnas: "))
For i = 1 To n
For j = 1 To m
A(i, j) = Val(InputBox("X( " & i & " , " & j & ")"))
Next
Next
End Sub
La emisión (impresión) elegante de los resultados:
Sub SalidaMatriz(n, m, xMat)
xCad = ""
For i = 1 To n
For j = 1 To m
xCad = xCad + Str(xMat(i, j)) + Space(5)
Next
xCad = xCad + Chr(13)
Next
MsgBox xTexto + Chr(13) + xCad
End Sub
Los procedimientos de cálculo:
Sub MatrSuma(n, m, A, B, C)
For i = 1 To n
For j = 1 To m
C(i, j) = A(i, j) + B(i, j)
Next
Next
End Sub
Sub MatrProd(n, m, p, A, B, C)
For i = 1 To n
For j = 1 To p
C(i, j) = 0
Next
Next
For i = 1 To n
For j = 1 To p
For k = 1 To m
C(i, j) = C(i, j) + A(i, k) * B(k, j)
Next
Next
Next
End Sub
Sub MatrDeterm(nA, A, C, d)
Call MatrInversa(nA, A, C, d)
End Sub
Finalmente, el procedimiento que permite invertir la matriz:
Sub MatrInversa(n, A, C, xDet)
For i = 1 To n
For j = 1 To n
If i = j Then
C(i, j) = 1
Else
C(i, j) = 0
End If
Next
Next
xDet = 1
For i = 1 To n
xP = A(i, i)
xDet = xDet * xP
For j = 1 To n
A(i, j) = A(i, j) / xP
C(i, j) = C(i, j) / xP
Next
For k = 1 To n
If i <> k Then
xP = A(k, i)
For j = 1 To n
A(k, j) = A(k, j) - xP * A(i, j)
C(k, j) = C(k, j) - xP * C(i, j)
Next
End If
Next
Next
End Sub
Nota:
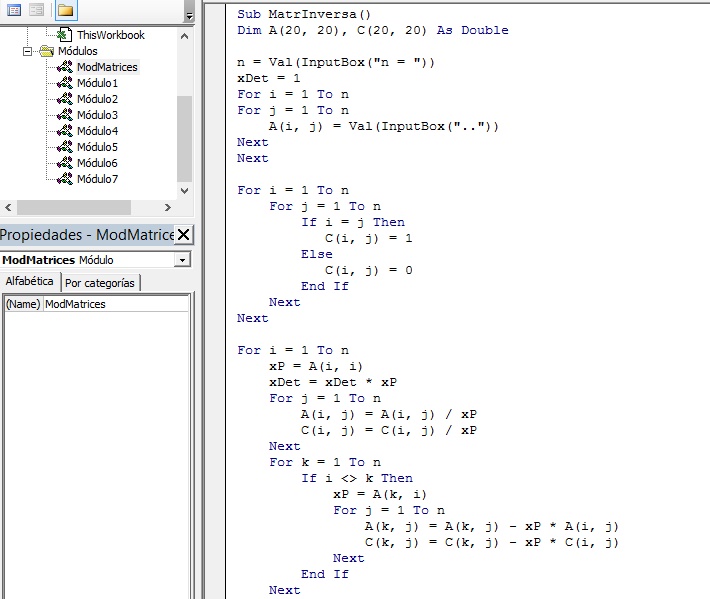
En el xMatInversa tenemos el procedimiento MatrInversa independiente de todo lo anterior que se puede usar sólo cuando se desea invertir una matriz regular.
Sub MatrInversa()
Dim A(20, 20), C(20, 20) As Double
n = Val(InputBox("n = "))
xDet = 1
For i = 1 To n
For j = 1 To n
A(i, j) = Val(InputBox(".."))
Next
Next
For i = 1 To n
For j = 1 To n
If i = j Then
C(i, j) = 1
Else
C(i, j) = 0
End If
Next
Next
For i = 1 To n
xP = A(i, i)
xDet = xDet * xP
For j = 1 To n
A(i, j) = A(i, j) / xP
C(i, j) = C(i, j) / xP
Next
For k = 1 To n
If i <> k Then
xP = A(k, i)
For j = 1 To n
A(k, j) = A(k, j) - xP * A(i, j)
C(k, j) = C(k, j) - xP * C(i, j)
Next
End If
Next
Next
xC = ""
For i = 1 To n
For j = 1 To n
xC = xC + Str(C(i, j)) + " , "
Next
xC = xC + Chr(13)
Next
MsgBox xC
MsgBox xDet
End Sub
Incluimos una imagen del procedimiento principal.

En la siguiente sesión veremos el uso de objetos en el Excel
haga clic aquí