Como una aplicación de lo que hasta ahora hemos aprendido, codificaremos una macro que nos permita estimar los coeficientes de una ecuación de regresión lineal vibariada.

En Estadística, una ecuación de regresión lineal simple es aquella de la forma: Y = A + BX.

Tiene múltiples aplicaciones cuando se trata de explicar la variación de una variable en función de la variación de otra. Por ejemplo: Cuando la demanda del pollo baja, el precio disminuye o, si la demanda aumenta, el precio se incrementa. Esto lo saben todas las personas que diariamente deben lidiar con el pollo.

Si X es la cantidad requerida de pollo, diariamente, e Y es el precio (por kilo) entonces,

Y = A + BX
 

me permite saber en cuánto se incrementará el precio del pollo, por cada cada unidad de incremento del mismo. Esto es estimación, predicción o proyección que es imprescindible en la economía del pollo. Para ello es suficiente saber el valor de "A" y "B", que constituyen los coeficientes de regresión lineal.

Para estimar (calcular) A y B, es necesario tener datos de la venta del pollo recogidos durante una semana o 15 días.

Las fórmulas que nos permiten calcular A y B son las que se muestran en la siguiente imagen.

Ahora vamos a codificar una macro que nos permita estimar (calcular) estos coeficientes.

Abra el archivo "Mis Macros.xlsm" o haga clic aquí

Vaya al editor del VBA e inserte un nuevo módulo.
Digite Sub RegreLineal y presione . Luego del cual, debe aparecer:

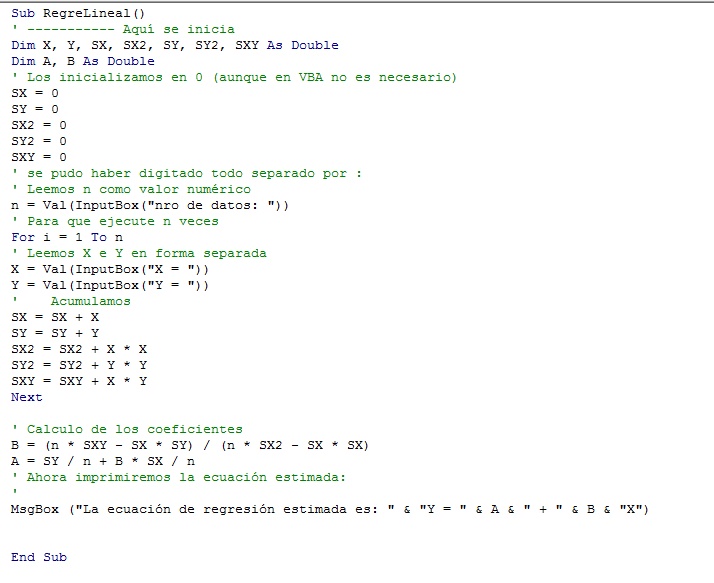
Sub RegreLineal()


End Sub

Usaremos todos los comentarios que sean necesarios a fin de que se entienda el programa
Al interior del procedimiento, digite lo siguiente:

' ----------- Aquí se inicia
DIM X, Y, SX, SX2, SY, SY2, SXY as Double
DIM A, B as Double ' Los inicializamos en 0 (aunque en VBA no es necesario)
SX = 0
SY = 0
SX2 = 0
SY2 = 0
SXY = 0
' se pudo haber digitado todo separado por :
' Leemos un valor para "n" y lo convertimos en valor numérico que nos indicará el número de pares (X, Y) que vamos a leer
n = Val(InputBox("Nro de datos: "))
' Para que ejecute n veces
' Las siguientes líneas, contenidas en el For ... Next, nos permiten leer n datos para X y n datos para Y.
For i = 1 to N
' Leemos X e Y en forma separada
X = Val(InputBox("X = "))
Y = Val(InputBox("Y = "))
' Acumulamos
SX = SX + X
SY = SY + Y
SX2 = SX2 + X*X
SY2 = SY2 + Y*Y
SXY = SXY + X*Y
Next
 

Ahora ya tenemos las sumatorias requeridas. Nos falta obtener los valores de A y B.

Continuemos:
' Calculo de los coeficientes
B = (n*SXY-SX*SY)/(n*SX2-SX*SX)
A = SY/n+B*SX/n
' Ahora imprimiremos la ecuación estimada:
'
MsgBox("La ecuación de regresión estimada es: " & "Y = " & A & " + " & B & "X")

Es todo, digite con cuidado el MsgBox (está imprimiendo Y = A + BX)
 

La macro debe ser la siguiente:

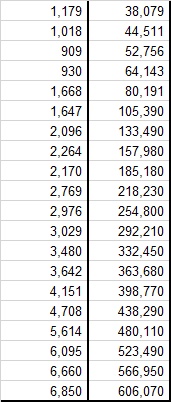
La siguiente imagen contiene los datos que se debe ingresar para este problema.

El valor para n debe ser 20
 

Grabe el archivo con el mismo nombre.
En la siguiente sesión veremos el uso de declaraciones condicionales. Para ello haga clic aquí