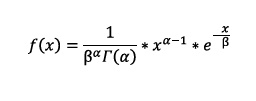
En esta sesión haremos uso de nuestro ingenio para plotear las clásicas funciones de distribución continuas especiales:

a. Distribución Gamma
b. Distribución Chi Cuadrado
c. Distribución t de Student
d. Distribución F de Fisher

En cada caso, presentaremos la función de densidad y trazaremos 5 gráficas variando el valor de sus parámetros.

Distribución Gamma

Su función de densidad

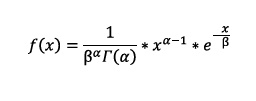
Generamos los valores en el Eje X
>x=seq(0,20,by=0.05)

Definimos los grados de libertad ( a = n, b = m)
> n1=8; m1=3
> n2=2; m2 = 8
> n3=10; m3 = 5
> n4=6; m4 = 2
> n5=4; m5 = 6

Definición de las variables
>x=seq(0,50,by=0.1)
>g1=1/(m1**n1*factorial(n1))*x**(n1-1)*exp(-x/m1)
>g2=1/(m2**n2*factorial(n2))*x**(n2-1)*exp(-x/m2)
>g3=1/(m3**n3*factorial(n3))*x**(n3-1)*exp(-x/m3)
>g4=1/(m4**n4*factorial(n4))*x**(n4-1)*exp(-x/m4)
>g5=1/(m5**n5*factorial(n5))*x**(n5-1)*exp(-x/m5)

Trazamos las gráficas

> plot(g1,col="red",xlab="",ylab="",type="l")
> legend(“topright”, legend = "Linea 1",col="red",text.font=2,bg="grey")
> legend(1,0.005, legend = "Linea 1",col="red")

Para no tener problemas en el rango del Eje Y, definamos los tamaños en un rango

> rango=range(0,g1,g2,g3,g4,g5)

Trazamos las gráficas y para que todas vayan en la misma Ventana, usamos la función par().

> plot(g1,col="red",xlab="",ylab="",type="l",ylim=rango)
> par(new=TRUE)
> plot(g2,col="black",xlab="",ylab="",type="l",ylim=rango)
> par(new=TRUE)
> plot(g3,col="green",xlab="",ylab="",type="l",ylim=rango)
> par(new=TRUE)
> plot(g4,col="blue",xlab="",ylab="",type="l",ylim=rango)
> par(new=TRUE)
> plot(g5,col="magenta",xlab="",ylab="",type="l",ylim=rango)
>legend("topright",legend=c("n=8,m=3","n=2,m=8","n=10,m=5","n=6,m=2","n=4,m=6"),col= c("red","black","green","blue","magenta"),lty=1:5,cex=0.8)

Observación:

La posición de la leyenda debe ser el P(x,y) de la ventana, de acuerdo a los valores de X e Y.

Distribución Chi Cuadrado

Su función de densidad

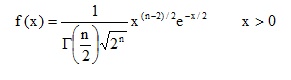
Usaremos los mismos grados de libertad del numerador
Definimos las variables
>n1=8;n2=2;n3=10;n4=6;n5=4
> ch1=1/(factorial(n1/2)*sqrt(2**n1))*x**((n1-2)/2)*exp(-x/2)
> ch1=1/(factorial(n2/2)*sqrt(2**n2))*x**((n2-2)/2)*exp(-x/2)
> ch1=1/(factorial(n3/2)*sqrt(2**n3))*x**((n3-2)/2)*exp(-x/2)
> ch3=1/(factorial(n3/2)*sqrt(2**n3))*x**((n3-2)/2)*exp(-x/2)
> ch2=1/(factorial(n2/2)*sqrt(2**n2))*x**((n2-2)/2)*exp(-x/2)
> ch1=1/(factorial(n1/2)*sqrt(2**n1))*x**((n1-2)/2)*exp(-x/2)
> ch4=1/(factorial(n4/2)*sqrt(2**n4))*x**((n4-2)/2)*exp(-x/2)
> ch5=1/(factorial(n5/2)*sqrt(2**n5))*x**((n5-2)/2)*exp(-x/2)

Trazamos la primera gráfica
> plot(ch1,col="red",xlab="",ylab="",type="l",ylim=rango)
Para insertar otro gráfico en la misma ventana
> par(new=TRUE)
Hacemos lo mismo con las otras variables
> plot(ch2,col="blue",xlab="",ylab="",type="l",ylim=rango)

> par(new=TRUE)
> plot(ch3,col="magenta",xlab="",ylab="",type="l",ylim=rango)

> par(new=TRUE)
> plot(ch4,col="green2",xlab="",ylab="",type="l",ylim=rango)

> par(new=TRUE)
> plot(ch5,col="black",xlab="",ylab="",type="l",ylim=rango)
legend("topright",legend=c("n=8","n=2","n=10","n=6","n=4"),col= c("red","black","green","blue","magenta"),lty=1:5,cex=0.8)

Distribución t de Student

Su función de densidad es

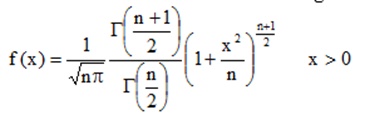
Ojo:

El exponente del último factor debe ser negativo.

Definamos los grados de libertad
> n1=1
> n2=5
> n3=10
> n4=30
> n5=120
>t1=1/sqrt(n1*pi)*factorial((n1+1)/2)/factorial(n1/2)*(1+x*x/n1)**(-(n1+1)/2)
> t2=1/sqrt(n2*pi)*factorial((n2+1)/2)/factorial(n2/2)*(1+x*x/n2)**(-(n2+1)/2)
> t3=1/sqrt(n3*pi)*factorial((n3+1)/2)/factorial(n3/2)*(1+x*x/n3)**(-(n3+1)/2)
> t4=1/sqrt(n4*pi)*factorial((n4+1)/2)/factorial(n4/2)*(1+x*x/n4)**(-(n4+1)/2)
> t5=1/sqrt(n5*pi)*factorial((n5+1)/2)/factorial(n5/2)*(1+x*x/n5)**(-(n5+1)/2)

Definimos a x como
>x=seq(-10,10,0.1)
Ploteamos las variables
> plot(t1,col="red",xlab="",ylab="",type="l")

> par(new=TRUE)
> plot(t2,col="black",xlab="",ylab="",type="l")

> par(new=TRUE)
> plot(t3,col="green",xlab="",ylab="",type="l")

> par(new=TRUE)
> plot(t4,col="blue",xlab="",ylab="",type="l")

> par(new=TRUE)
> plot(t5,col="magenta",xlab="",ylab="",type="l")
>legend("topright",legend=c("n=1","n=5","n=10","n=30","n=120"),col= c("red","black","green","blue","magenta"),lty=1:5,cex=0.8)

Distribución F de Fisher

Su función de densidad

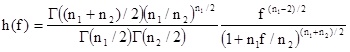
Definamos los grados de libertad del numerador y denominador

>n1 = 6; m1 = 26
>n2=20; m2=20
>n3=50; m3=50
>n4=3;m4=30
>n5=25;m5=5
Definamos los valores de X
> x=seq(0.1,50,0.1)

Ahora las variables F
>f1=factorial((n1+m1)/2)*(n1/m1)**(n1/2)/(factorial(n1/2)*factorial(m1/2))*x**((n1-2)/2)/(1+n1*x/m1)**((n1+m1)/2)
> f2=factorial((n2+m2)/2)*(n2/m2)**(n2/2)/(factorial(n2/2)*factorial(m2/2))*x**((n2-2)/2)/(1+n2*x/m2)**((n2+m2)/2)
> f3=factorial((n3+m3)/2)*(n3/m3)**(n3/2)/(factorial(n3/2)*factorial(m3/2))*x**((n3-2)/2)/(1+n3*x/m3)**((n3+m3)/2)
> f4=factorial((n4+m4)/2)*(n4/m4)**(n4/2)/(factorial(n4/2)*factorial(m4/2))*x**((n4-2)/2)/(1+n4*x/m4)**((n4+m4)/2)
> f5=factorial((n5+m5)/2)*(n5/m5)**(n5/2)/(factorial(n5/2)*factorial(m5/2))*x**((n5-2)/2)/(1+n5*x/m5)**((n5+m5)/2)
> plot(f1,col="red",xlab="",ylab="",type="l",ylim=rango,xlim=c(0,max(x)))
> par(new=TRUE)
> plot(f2,col="black",xlab="",ylab="",type="l",ylim=rango,xlim=c(0,max(x)))

> par(new=TRUE)
> plot(f3,col="green",xlab="",ylab="",type="l",ylim=rango,xlim=c(0,max(x)))

> par(new=TRUE)
> plot(f4,col="blue",xlab="",ylab="",type="l",ylim=rango,xlim=c(0,max(x)))

> par(new=TRUE)
> plot(f5,col="magenta",xlab="",ylab="",type="l",ylim=rango,xlim=c(0,max(x)))
La leyenda
> legend(“topright”,legend=c("n=6,m=26","n=20,m=20","n=50,m=50","n=3,m=30","n=25,m=5"), col= c("red","black","green2","blue","magenta"),lty=1:5,cex=0.8)

Continuaremos en la siguiente sesión