Para terminar las sesiones de gráficos, veremos algunos ejemplos de gráficos en tres dimensiones. Esto está más relacionado con funciones matemáticas de la forma z = f(x,y) o en la forma f(x,y,z) = 0.
Por ejemplo
z = x2+y
z = 64-x2+y
z = 2xy + x2+y
Empecemos por lo más sencillo: Los diagramas de dispersión en 3D.
Abra el archivo modgraficos.py. Vaya al final y, dejando una o más líneas, ingrese lo que corresponde a la primera función: gr3d01()
def gr3d01():
Primero vamos a definir las listas que conendrán los valores a plotear. En 3 dimensiones, necesitamos los puntos en el eje X: x sobre la cual se levantarán los otros valores; primero en el plano: y y luego en el eje vertical: z. Por su puesto que en un diagrama normal de dispersión es la variable 1 vs la variabe 2, en el espacio serán tres variables. La siguiente gráfica nos muestra este diagrama.
Los datos:
x = range(1,16)
y = [5,7,3,9,12,15,7,18,14,25,32,16,22,35,28]
z = [15,27,33,29,42,75,47,38,84,95,42,66,82,55,88]
#
La variable X, en ese rango, toma valores de 1 a 15.
Aumentemos más variables para emitir la dispersión de varios tripletas de datos.
t = [125,217,133,219,242,275,147,238,184,295,242,166,282,255,188]
u = [-25,-17,-33,-19,-42,-75,-47,-38,-84,-95,-42,-66,-82,-55,-88]
v = [15,27,33,-29,42,-75,-47,38,84,-95,-42,-66,-82,55,88]
#
Ahora vamos a configurar el plano tridimensional
Para la primera gráfica
fig1 = plt.figure(1)
pxy = fig1.add_subplot(111,projection="3d")
Deje 5 líneas en blanco, indentada (es suficiente que presione [Intro]. Allí colocaremos todo lo que se refiera a la primera gráfica. Lo que viene corresponderá a la segunda gráfica.
Para la segunda gráfica
fgi2 = plt.figure(2)
pxz = fig2.add_subplot(111,projection="3d")
Procedemos a trazar el diagrama usando la función scatter(...), que significa dispersión. Como trazar tres diagramas en la primera: (x,y,z). Usaremos los colores "g", "r" y "b" y como forma de los puntos, los marcadores "*","o", "+".
En la primera gráfica:
pxy.scatter(x,y,z,c="g",marker="*")
pxy.scatter(x,t,u,c="r",marker="o")
pxy.scatter(x,u,v,c="b",marker="+")
#
Después de estas líneas y para mostrar sólo la gráfica de estos puntos, digite
plt.show()
naturalmente respetando la identación
Grabe el archivo modgraficos.py y ejecútelo usando [Run] - [Run module]. Cuando termine, en la consola digite: gr3d01() y presione [Intro].
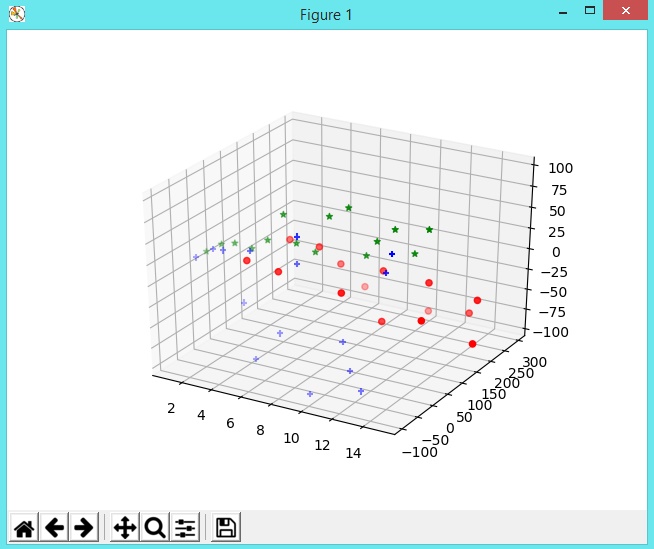
La gráfica a obtenerse será lo que muestra la siguiente imagen

Con el puntero del ratón dentro del diagrama, muévalo en cualquier dirección
Esto es lo que se muestra en la siguiente imagen
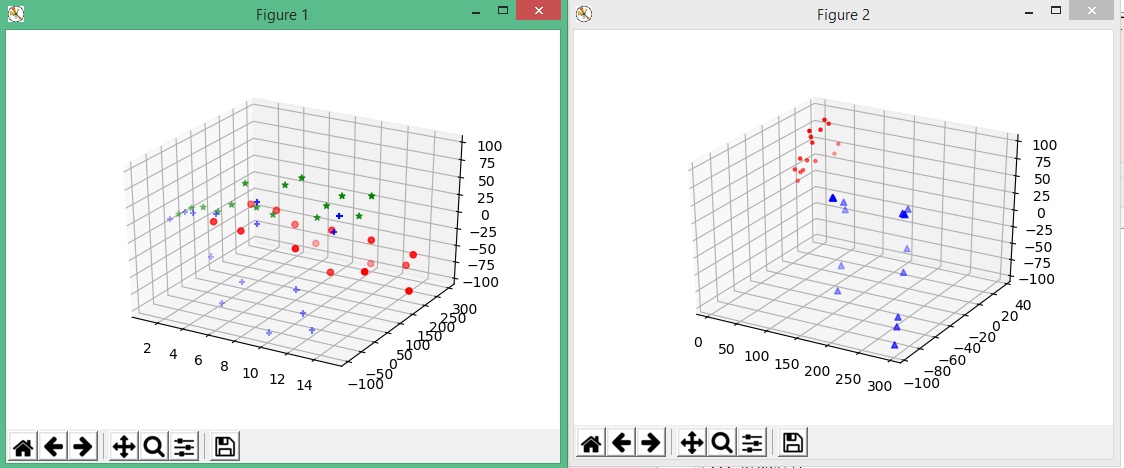
Ahora para la segunda ventana, trazaremos los verdaderos diagramas de dispersión:
Para ello cambiemos los valores de x
x = [5,7,3,9,12,15,7,18,14,25,32,16,22,35,28]
pxz.scatter(x,y,z,c="r",marker=".")
pxz.scatter(t,u,v,c="b",marker="^")
#
Al final debe digitar
plt.show()
Puede apreciar que hemos definido a x como un conjunto de datos.
Antes de la instrucción plt.show() del primer gráfico, digite # para convertir esta línea en comentario no ejecutable.
Grabe el archivo y ejecútelo para disponer del modo interpretativo del Pyhon.
La función debe quedar de la siguiente forma:
def gr3d01():
x = range(1,16)
y = [5,7,3,9,12,15,7,18,14,25,32,16,22,35,28]
z = [15,27,33,29,42,75,47,38,84,95,42,66,82,55,88]
#
t = [125,217,133,219,242,275,147,238,184,295,242,166,282,255,188]
u = [-25,-17,-33,-19,-42,-75,-47,-38,-84,-95,-42,-66,-82,-55,-88]
v = [15,27,33,-29,42,-75,-47,38,84,-95,-42,-66,-82,55,88]
#
fig1 = plt.figure(1)
pxy = fig1.add_subplot(111,projection="3d")
pxy.scatter(x,y,z,c="g",marker="*")
pxy.scatter(x,t,u,c="r",marker="o")
pxy.scatter(x,u,v,c="b",marker="+")
#
#plt.show()
#
fig2= plt.figure(2)
pxz = fig2.add_subplot(111,projection="3d")
x = [5,7,3,9,12,15,7,18,14,25,32,16,22,35,28]
pxz.scatter(x,y,z,c="r",marker=".")
pxz.scatter(t,u,v,c="b",marker="^")
#
plt.show()
No se olvide que la cabecera del archivo madgraficos.py, el que estamos editando, debe contener:
Cuando sólo quiera mostrar la primera gráfica, quite el "#" de plt.show() y al correrla y ejecutarla por la consola digitando gr3d01(), tendrá sólo la primera gráfica.
import pandas as pd
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.cm as cm
from pylab import *
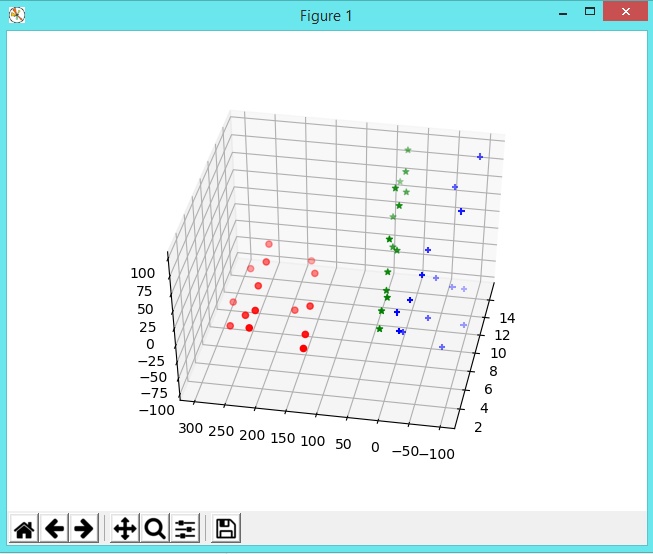
En la consola sólo digite gr3d01() y presione [Intro].
Esto es lo que obtendrá
Creo que completaremos una parte de diagramas de dispersión en 3D si los datos provienen de un archivo, que es lo usual que ocurra cuando de realizar aplicaciones reales, se trate.
La función anterior, con algunas modificaciones, nos permitirá crear una función, grFromFile(...) que nos permitirá resolver estas siuaciones.
Vamos a insertar esta función al final del archivo modgraficos.py.
Puesto que hasta ahora, nuestros módulos y funciones, cuando se trata de usar variables grabadas en archivos de texto, las hemos tenido que leer en el mismo módulo o función, de manera que si cambiamos de archivo, debemos modificar el módulo o función, en este caso queremos independizar el módulo o función de los datos a procesar.
Nuestra función va a pedir el nombre del archivo, donde se incluya la ruta completa y la lista de los nombres de las variables, separados por coma.
Por eso la cabecera y las líneas que habilitan los datos para graficar, será las siguientes:
def grFromFile(fname,varname):
vn =[]
vn = varname.split(",")
datos = pd.read_csv(fname,sep="\t",names=vn)
y = datos[vn[0]]
x1 = datos[vn[1]]
x2 = datos[vn[2]]
x3 = datos[vn[3]]
Antes de invocar a la función, en consola se debe definir en una variable la ruta y nombre del archivo y en otra, la lista de los nombres de las variables. Esto lo recibirá la función en fname y varname, respectivamente. Luego del cual, se extreará los elementos de varname hacia una lista, vn. Se leerá los datos gracias a pandas y se extraerán los datos variable por variable, usando como los elementos de la lista vn.
A continuación se definirá los valores en el eje X, para plotear las variables y y z por encima (o debajo) del plano XY.
Esto lo conseguimos con
X = range(1,len(y)+1)
Luego vendrá las instrucciones del ploteo:
pxy = fig.add_subplot(111,projection='3d')
pxy.scatter(X,y,x1,c="r",marker="*")
pxy.scatter(X,y,x2,c="g",marker="^")
pxy.scatter(X,y,x3,c="b",marker="o")
plt.show()
La función completa debe quedar así:
def grFromFile(fname,varname,separador):
vn =[]
vn = varname.split(",")
datos = pd.read_csv(fname,sep=separador,names=vn)
y = datos[vn[0]]
x1 = datos[vn[1]]
x2 = datos[vn[2]]
x3 = datos[vn[3]]
X = range(1,len(y)+1)
fig =plt.figure()
pxy = fig.add_subplot(111,projection='3d')
pxy.scatter(X,y,x1,c="r",marker="*")
pxy.scatter(X,y,x2,c="g",marker="^")
pxy.scatter(X,y,x3,c="b",marker="o")
plt.show()
Ahora grabe el archivo y ejecute usando RUN de forma que se tenga la forma ejecutable del mismo.
Vamos a probar con el archivo agri.txt que contiene 4 variabes: Producción agrícola, Volumen de fitosanitarios, Parque automotor y Financiamiento Público y privado.
Estando en la consola creamos las variables:
>>>x = "d:\\pypage\\agri.txt"
>>>y = "Pa,Vf,Pm,Fp"
>>>s = "\t"
Luego invocamos a la función:
>>>grFromFile(x,y,s)
Y se acabó.
En la siguiente imagen se tiene el diagrama de dispersion:
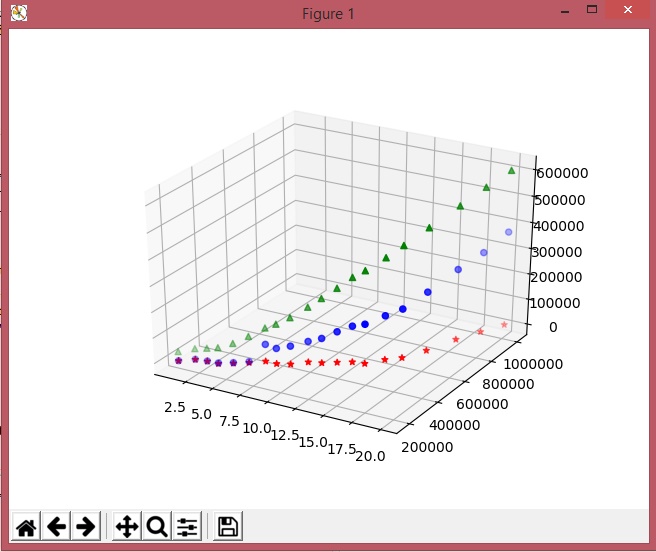
A continuación codificaremos otras funciones en las cuales usaremos funciones matemáticas con el objeto de familiarizarnos con gráficos 3D y las librerías que son necesarias
La función gr3d02(), usará tres variables: x, que será generada desde -3*pi hasta 3*pi, con 100 valores.
x = np.linspace(-3*np.pi,3*np.pi,100);
Las funciones y y z de la siguiente forma:
y = x*np.sin(x)
z = np.cos(x);
La preparación del ploteo mediante una sentencia for que ploterá pares de valores por encima del plano XY (z>0) de color rojo "r"
Luego se ploteará las tres variables de color "b".
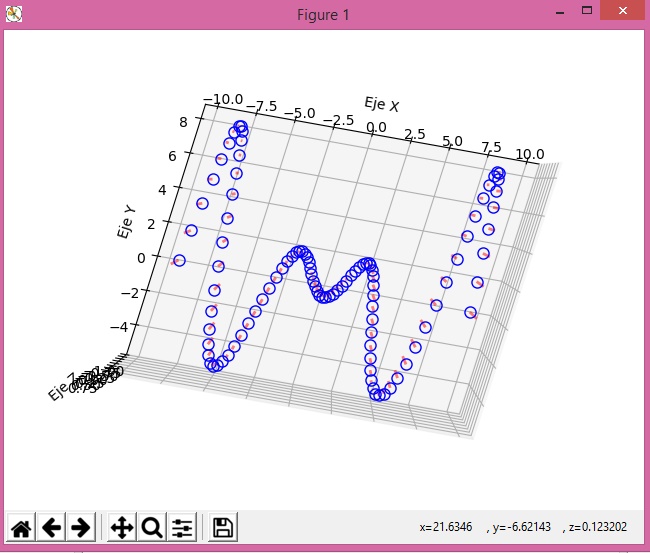
El código de la función es la siguiente:
def gr3d02():
x = np.linspace(-3*np.pi,3*np.pi,100);
y = x*np.sin(x)
z = np.cos(x);
fig = plt.figure()
ax = Axes3D(fig)
for i in range(len(x)):
ax.plot([x[i],x[i]],[y[i],y[i]], [0,z[i]],"--",linewidth=2,color="r",alpha=0.5)
ax.plot(x,y,z,"o",markersize=8,
markerfacecolor="none",color = "b",label="ib")
ax.set_xlabel("Eje X")
ax.set_ylabel("Eje Y")
ax.set_zlabel("Eje Z")
plt.show()
Incluya esta función al final del archivo modgraficos.py. Luego ejecute grabando para actualizar.
Ejecute desde la consola digitando gr3d02().
Ahora, haciendo clic dentro del gráfico, busque diversos planos de vista de la gráfica.
Puesto que no requiere de parámetros, la gráfica será emitida.