
La estadística que se ocupa del estudio de los fenómenos poblacionales cuyo comportamiento no es conocido se conoce como la estadística no paramétrica, en contraste con aquella cuya distribución y parámetros son conocidos. En la estadística paramétrica las afirmaciones o supuestos que se formulan como parte de un proceso inferencial, se realiza sobre los parámetros.
No teniendo o siendo desconocido los parámetros, la estadística no paramétrica formula supuestos comparando la mediana con un valor supuesto o entre las medianas, si se trata de más de una muestra.
Otra razón por la que se emplean estas pruebas es por el tamaño de la muestra. Si su tamaño es mayor de 15 ó 20, se puede usar la distriución noramal para probabr los supuestos.
Una de sus desventajas es que no son tan eficientes y por tanto el riesgo es mayor en las decisiones que se tomen.
Hay muchos test o pruebas no paramétricas.
Nuestro propósito es obtener el estadístico de la prueba y contrastarla con los valores de las tablas que para dichas pruebas exisen. Del mismo modo calcularemos el estadístico usado para la normal cuando el tamaño de la muestra es mayor.
Esta prueba se utiliza cuando: - El tamaño de muestra es pequeño
- Las diferencias(dato - mediana supuesta) son ordinales o continuas - Las pruebas se realizan sobre la mediana y en algunos casos es sobre la media - Los diferencias son independientes
La variable a ser analizada resulta de la diferencia del dato menos la mediana supuesta
El estadístico T = Min(R-, R+), donde R- es la suma de las diferencias negativas y R+ es la suma de las diferencias posiivvas. Se descarta cuando hay empate.
Con un nivel de significación que puede ser del 100α (en general α = 0.05) se compara con las tablas respectivas para aceptar o no la hipótesis nula.
Si el tamaño de muestra es superior a 15 ó 20, debemos obtener la media μT y varianza σ2T.
Con los cuales se calcula la media y varianza para obtener el Zc y comprobarlo por la normal.

Ejemplo
Algunos clientes se han quejado sobre los tiempos de duración de las pilas producidas por una empresa. Se tomó una muestra y se midió su duración. ¿Se puede concluir que la mediana de la duración de las pilas es diferente a 18?
Solución
Los datos
La mediana
>>>m = 18
Los datos:
>>>pila=[18.4,19.0,17.0,17.0, 18.6, 17.2, 19.2, 17.1, 18.5, 16.0, 16.1, 18.4, 16.9, 19.4, 16.8, 18.2, 18.4, 18.3, 18.1, 17.1]
Sea sn y sp las variables que contendrán las diferencias absolutas entre los elementos de la pila y m, la mediana supuesta.
>>>sn = 0
>>>sp = o
Sumaremos en sn el valor absoluto de la diferencia entre pila[i] y m, que pila[i] < m; en caso contario, sumaremos dicho valor se añadirá a sp.
for i in range(len(pila)):
if pila[i] < m:
sn = sn + abs(Lista[i]-m)
elif Lista[i]>m:
sp = sp + abs(Lista[i]-m)
Para obtener el estadístico T, debemos elegir el menor de las sumas.
T = np.min([sn,sp])
Ahora, decidimos si el tamaño de la muestra es superior a 15, en cuyo caso se calcula Zt que se contrastará con el Z teórico con el 5% de significación.
if len(Lista)>15:
Zt = (T-n*(n+1)/4)/np.sqrt((n*(n+1)*(2*n+1))/24)
print("Estadistico: ",T,"\n\nValor de Zc = ",Zt)
Todo esto se recoje en una función llamada Wilcoxon, que deberemos colocar en un archivo nuevo con el nombre noparamet.py.
Esta prueba compara dos muestras relacionadas de variables cuantitativas u ordinales. Permite comprobar si dos poblaciones son equivalentes en su posición definida por sus medianas.
Ejemplo
Se tomó una muestra de pacientes que se sometieron a una determinada dieta para bajar de peso. Se desea saber si la dieta tuvo efecto.
Solución
Los datos son los siguientes:
>>> pin = [80,70,68,75,72,85,90,75,85,80]
>>> pfin=[75,68,68,70,74,60,75,70,80,79]
Para realizar la prueba, usaremos el test de Wilcoxon que pertenece a la librería del paquete scipy.stats que la importaremos
>>>from scipy import stats as st
Usaremos:
scipy.stats.wilcoxon(x, y=None, zero_method='wilcox', correction=False, alternative='two-sided')
Por simplicidad, st es el alias de scipy.stats
Las dos series son: x e y.
zero_method puede ser: "wilcox","pratt", "zsplit": El primero no toma en cuenta las diferencias que son ceros, la segunda sí. Por defecto es "wilcoxon".
alternative, puede ser "less", "greater", "two-sided". Por default es "two-sided". Pasamos a ejecutarlo
>>>st.wilcoxon(pin,pfin)
Los resultados:
WilcoxonResult(statistic=2.5, pvalue=0.01672972298927249)
Interpretación:
El estadístico T = 2.5 que se puede comparar con el de la tabla correspondiente.
pValue = 0.017. Significa que, al 5% de nivel de significación, se debe rechazar la hipóesis nula; es decir, que la prueba sí tuvo efecto.
La función que definiremos para el caso de dos muestras será:
def Wilcox2m(Lista1,Lista2):
res = st.wilcoxon(pin,pfin)
print("\n\nEstadísico: ",res[0],"\npValue = ",res[1])
Esta prueba se puede usar para comparar dos muestras provenientes de dos poblaciones que satisfacen los siguientes criterios;
- Las dos muestras son aleatorias; es decir son representativas e independientes
- La medida en la muestra es una variable continua
- Por lo general la medida de comparacion hace uso de la simetria; es decir, se formuan las comparaciones con respecto a la mediana.
Ejemplo
En una academia militar, se trata de comparar la estatura de los alumnos de las secciones sec1 y sec2. Se sospecha que, si las estaturas son diferentes al 5% de significación, el rendimiento físico puede variar entre los alumnos de ambas secciones.
Los datos nos permiten definir las siguientes listas
>>>sec1 = [171.8,171.3,173.1,173.8,169.9,167.6,171.0,167.7,168.5,171.6,172.0,173.1,169.4,175.4,177.0]
>>>sec2 = [172.5,171.5,170.4,169.5,174.5,176.1,167.4,167.8,170.7,167.9,169.9,169.9,170.2,168.4,169.0]
La prueba para este caso es: scipy.stats.mannwhitneyu(x,y,use_continuity=True,alternative=None,sig-paren")
Como antes, usaremos el alias: st
>>>st.mannwhitneyu(sec1,sec2)
Esta nos dará como resultado:
MannwhitneyuResult(statistic=81.0, pvalue=0.09912805992906182)
De manera que, con un 5% de significación, podemos afirmar que no se rehaza la hipótesis nula; en consecuencia, no existe diferencia significativa en la altura de los alumnos de ambas secciones.
La función a ser incluida en el archivo noparamet.py será
def ManWith(Lista1, Lista2):
res = st.mannwhitneyu(sec1,sec2)
print("\n\nEstadísico: ",res[0],"\npValue = ",res[1])
Esta prueba tiene por objetivo probar si dos o más muestras provienen de poblaciones iguales o no difieren significativamente en su posición central; es decir, tienen la misma mediana.
Por otro lado, se usa esta prueba cuando en un diseño de experimento de un modelo totalmente aleatorizado, los datos no satisfacen las condiciones de normalidad y homogeneidad en las varianzas.
Sus caracterísicas son:
- Tienen una distribución continua
- Las muestras son inde pendientes
- Provienen de poblaciones cuyas localizaciones centrales (llámese medianas) no difieren en al menos una.
Para este caso, usaremos el paquete o librería scipy.stats que la debemos importar en primer término:
>>>from scipy import stats as st
Ejemplo
Una boutique tiene tres establecimientos o sucursales en centros comerciales. Se mantiene un registro del número de clientes que realmente compran en cada establecimiento. La siguiente es una muestra de estos datos:
ccPn: 99, 64, 101, 85, 79, 88, 97, 95, 90, 100
ccSb: 83, 102, 125, 61, 91, 96, 94, 89, 93, 75
ccSa: 89, 98, 56, 105, 87, 90, 87, 101, 76, 89
Utilizando la prueba de Kruskall-Wallis, ¿se puede afirmar,al 5% de significación, que sus tiendas tiene el mismo número de clienes que compran?
Solución
Primero almacenamos los datos en listas
>>>ccPn = [99, 64, 101, 85, 79, 88, 97, 95, 90, 100]
>>>ccSb = [83, 102, 125, 61, 91, 96, 94, 89, 93, 75]
>>>ccSa = [89, 98, 56, 105, 87, 90, 87, 101, 76, 89]
La hipótesis nula afirmará que el número de clientes en los tres establecimientos es la misma.
Para mayor precisión y evitar la carga de módulos que no son necesarios, la importación de las librerías pueden extraer algunos de sus módulos o funciones de interés. Esto es lo que queremos hacer ahora; cargar sólo el módulo kruskal con la siguiente instrucción:
>>>from scipy.stats.mstats import kruskal as sk
Ahora para usarlo, simplemente usamos
>>>kruskal(ccPn,ccSb,ccSa)
Los resultados que se obtienen son:
KruskalResult(statistic=0.19643493761140035, pvalue=0.9064517573370071
donde el estadístico H = 0.196435 y pValue = 0.9065
Esto quiere decir que no se rechaza la hipótesis nula; en consecuencia, existe suficiene evidencia para afirmar que la afirmación es cierta.
Nota:
Si la importación hubiera sido la anterior, los resultados son los mismos, lo que prueba que se trata de la misma función, sólo que la segunda evita cargar a memoria funciones que no se van a usar.
>>>st.kruskal(ccPn,ccSb,ccSa)
KruskalResult(statistic=0.19643493761140035, pvalue=0.9064517573370071)
Sin embargo, cabe resaltar que cargar sólo kruskal, permite trabajar con lista de listas de datos; es decir, podemos armar una lista de listas con los datos de las tres sucursales
Lista = [ccPn,ccSb,ccSa]
Ahora lo ejecutamos
>>> sk(lista)
Los resultados son los mismos.
KruskalResult(statistic=0.19643493761140035, pvalue=0.9064517573370071)
Pero al usar
>>> st.kruskal(lista)
Se produce un error que en su última línea podemos leer de que la instrucción esperaba por lo menos dos grupos.
Traceback (most recent call last):
File "
st.kruskal(lista)
File "C:\Users\Ilmer\AppData\Local\Programs\Python\Python37-32\lib\site-packages\scipy\stats\stats.py", line 5046, in kruskal
raise ValueError("Need at least two groups in stats.kruskal()")
ValueError: Need at least two groups in stats.kruskal()
La implementación de estas instrucciones en el archivo noparamet.py es la siguiente:
def KrusWall(Lista):
res = sk(Lista)
print("\n\nEstadísico: ",res[0],"\npValue = ",res[1])
Inclúyalo en el archivo , grabe y ejecútelo.
Como en el caso de la prueba de Kruskal-Wallis, esta prueba es una alternativa para cuando un problema que debe ser resuelto por el modelo de bloques aleatorizados del diseño de esperimento, no satisface las dos condiciones: La prueba de Normalidad y la prueba de Homogeneidad de varianzas.
Como en el caso anterior, la hipótesis de igualdad del comportamiento mediano en dos o más poblaciones, será recazada o no, con esta prueba
Ejemplo
Un grupo de investigadores desean probar que existe diferencia en el nivel de estrés laboral de los trabajadores de la empresa ABS luego de asistir a un taller sobre manejo de estrés en el trabajo. Sel seleccionó una muestra al azar de seis trabajadores quienes asistieron a un taller sobre manejo de estrés, además realizaron una medición de seguimiento un mes después de finalizado el taller. El nivel de estrés se midió en una escala de 1 hasta 5, donde 1 significa bajo estrés y 5 muy alto estrés. Los datos se muestran a continuación.
| Trabajador | Trab 1 | Trab 2 | Trab 3 | Trab 4 | Trab 5 | Trab 6 |
| Antes del taller | 2 | 2 | 1 | 3 | 3 | 2 |
| Después del taller | 4 | 4 | 3 | 5 | 5 | 4 |
| Seguimiento | 3 | 3 | 4 | 4 | 3 | 5 |
¿Podemos afirmar con 3% de significación que los niveles de estrés de los trabajadores son idénticos antes del taller para el manejo de estrés en el trabajo, después del taller y en el seguimiento?
Solución
Usaremos la libreria anterior
>>>from scipy import stats as st
Creamos las tres listas
>>> ant = [2,2,1,3,3,2]
>>> des = [4,4,3,5,5,4]
>>> seg = [3,3,4,4,3,5]
Ejecutamos la prueba
>>>st.friedmanchisquare(ant,des,seg)
Los resultados:
FriedmanchisquareResult(statistic=8.434782608695647, pvalue=0.01473703885272499)
Podemos afirmar que, al 3% de significación, los niveles de estrés no son iguales en los tres niveles de tratamiento.
Ejemplo
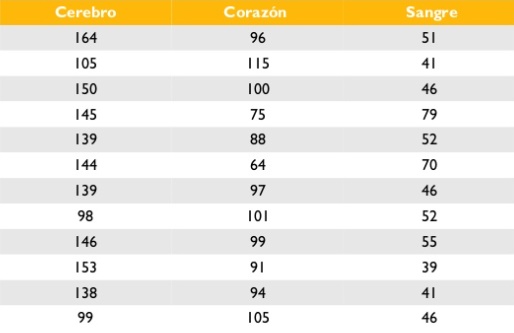
Con el objeto de estudiar la diferencia de concentración de un tóxico (mg/1000) en distintos órganos de peces, se extrae una muestra aleatoria de peces de un río y se estudia en cada uno de ellos la concentración del tóxico en el cerebro, corazón y la sangre. El objetivo del estudio es conocer si la concentración del tóxico en los tres órganos es igual o diferente.
Los datos son los siguientes:
Solución
Definimos las listas correspondientes:
cerebro = [164,105,150,145,139,144,139,98,146,153,138,99]
corazon = [96,115,100,75,88,64,97,101,99,91,94,105]
sangre = [51,41,46,79,52,71,46,52,55,39,41,46]
Ejecutamos la prueba
>>>st.friedmanchisquare(cerebro,corazon,sangre)
Estos son los resultados
FriedmanchisquareResult(statistic=15.166666666666657, pvalue=0.0005088621855732938)
Donde el estadístico de la prueba es T = 15.17
pValue = 0.0
Con lo cual, podemos afirmar que no existe suficiente evidencia para afirmar que la concentración de tóxico en los tres órganos sea la misma.
Si usamos
>>>from scipy.stats.mstats import friedmanchisquare as fr
Podemos usar
>>>x = [cerebro,corazon,sangre]
Luego ejecutar
>>>fr(x)
Los resultados:
FriedmanchisquareResult(statistic=15.166666666666666, pvalue=0.0005088621855732918)
Lo importante es que podemos usar una lista de listas de modo que cuando implementemos esta función en el archivo noparamet.py se podrá pasar los datos en una lista de listas y no individualmente pues no sabemos de cuántas muestras se trata en el problema.
El código que debemos incluir en el archivo noparamet.py es el siguiente:
def Friedman(Lista):
res = fr(Lista)
print("\n\nEstadísico: ",res[0],"\npValue = ",res[1])
En conclusión, la solución a problemas que demanden el uso de la estadística no paramétrica se encuentran en el archivo noparamet.py. La forma de invocar a una de las pruebas requiere de la conversión de los datos en listas y luego enviarlos a la función respectiva. Esto es lo que se hace en la parte principal de este archivo, como se puede observar en la siguiente imagen.
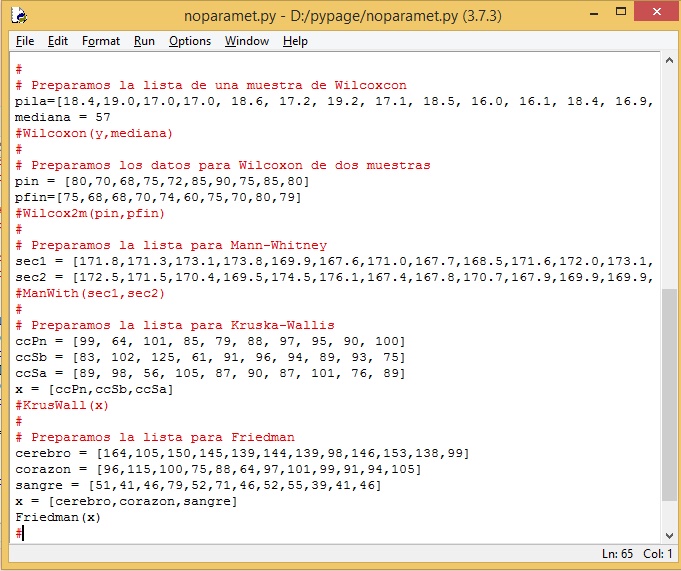
Observe que la única funció que está habilitada para invocarse es le de Friedman. Las otras están como comentario.
Observe también que allí es donde se prepara los datos para luego invocar la función correspondiente.
Continuar en la siguiente sesión