En esta página desarrollaremos el tema la construcción de gráficos en Python 3.7
Si bien la librería estándar de Python no incluye suncionalidad para la construcción de gráficos, disponemos de varias librerías que cubren una diversidad de tipos de gráficos bidimensionales y tridimensionales. Nuestro interés por ahora es la presentación de gráficos bidimensionales. Para ello vamos a usar las librerias de paylab, de matplotlib y otras que las iremos respentando en el desarrollo de este tema. Lógicamente, las librerías numpy y math serán necesarias pues en todos los casos de construcción de gráficos se manejan series que requieren de operaciones matemáticas.
Empecemos realizando gráficos en la consola. Después pasaremos a crear módulos al respecto.
Importemos las librerías mencionadas líneas arriba.
Librería numpy para operaciones matemáticas
>>>import numpy as np Librería pylab pues realizaremos gráficos interactivamente
>>>from pylab import * # Importa todas las funciones de gráficos
De matplotlib importaremos el módulo pyplot
>>>import matplotlib.pyplot as plt
La función arange(...), un derivado de range(...), nos permite generar un conjunto de valores secuenciales que nos servirán para construir funciones y = f(x) y, en un gráfico, constituirán los valores del eje X.
Vamos a generar numéros desde -3.1141592 hasta 3.141592, variando en 0.05
>>>x = np.arange(-pi,pi,0.02)
>>>len(x) # Tenemos 315 valores de x para construir cualquier función matemática
Calculamos el seno para la varible x
>>>s = np.sin(x)
Lo ploteamos
>>>plt.plot(s)
Tenemos que usar la sentencia show() para mostrar el gráfico en otra ventana
>>>plt.show()
Para retornar a la consola, se debe cerrra la ventana del gráfico.
Como puede ver, el eje X no tiene los valores que le corresponden a cafa f(x) que genera la curva graficada
Vamos a incluirla
>>>plt.plot(x,s)
>>>plt.show()
Cambiemos de color del gráfico
>>>plt.plot(x,s,"r") # r de red
>>>plt.show()
Grafiquemos las funciones de seno y coseno a la vez
>>>plt.plot(x,s,"r")
>>>plt.plot(x,np.cos(x),"b") >>>plt.show() Ahora veamos otra forma de plotear lo mismo
>>> s = plt.plot(np.sin(x),"b")
>>> c = plt.plot(np.cos(x),"r")
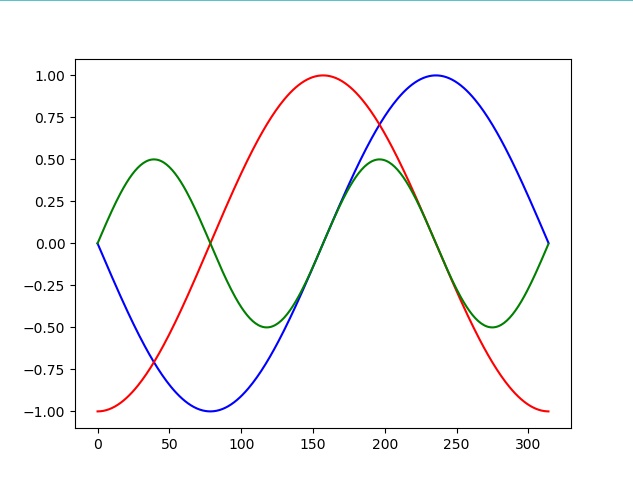
>>> sc = plt.plot(np.exp(-x)*np.sin(x)*np.cos(x),"g")
Generamos una lista de estos gráficos y mostramos
>>> g = [s,c,sc]
>>> plt.show()
La siguiente imagen muestra este gráfico

Ahora vean lo que podemos hacer:
Primero generamos los valores a = f(x)
>>> a = np.sin(x)
>>> b=np.cos(x)
>>> d = a*b
Luego lo ploteamos como a una lista de variables
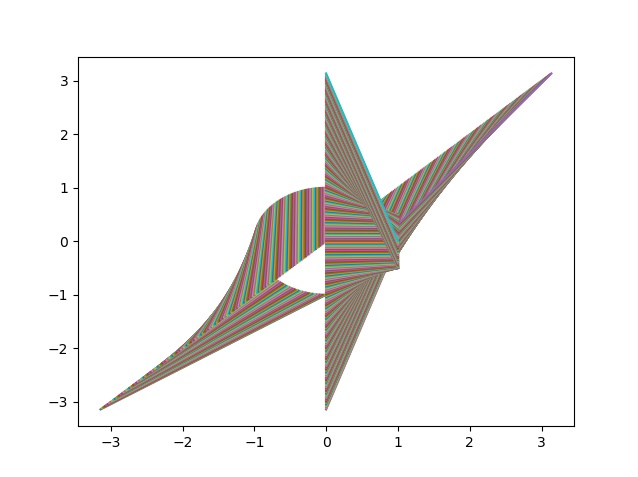
>>> plt.plot([x,a],[x,b],[x,d])
>>> plt.show()
La siguiente imagen nos muestra este gráfico
Continuemos. Veamos ahora gráfico de líneas de algunos valores
>>>x = np.arange(1,11)
>>>a = [12,15,13,17,18,10,6,15,12,18]
La gráfica a con eje x
>>>plt.plot(a)
>>>plt.show()
De color rojo, con eje y con líneas concectadas
>>> plt.plot(x,a,"r-")
>>> plt.show()
Gráfico en azul con puntos y sin conexión
>>> plt.plot(x,a,"b.")
>>> plt.show()
En rojo, con punto y líneas conectadas
>>> plt.plot(x,a,"ro-")
>>> plt.show()
Agreguemos otras variables al ploteo de líneas.
Definamos la variable b:
>>> b = [2,5,3,7,8,9,6,5,2,8]
Ahora ploteamos ambas variables con el mismo eje x
plt.plot(x,a,b)
plt.show()
Ploteemos la variable a contra b, con líneas conectadas
>>>plt.plot(a,b)
>>>plt.show()
Será que sin línea de conexión obtenemos un digrama de dispersión?
>>> plt.plot(a,"*",b,"*")
>>> plt.show()
Y qué pasa si le añadimos color a cada ploteo?
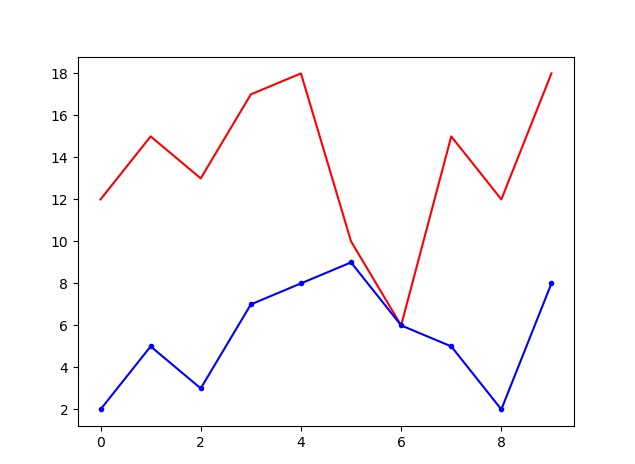
>>> plt.plot(a,"r-",b,"b.-")
>>> plt.show()
No es cierto, son gráfica de puntos independiente una de otra variable.
La siguiente imagen correspondiente a esta gráfica lo demuestra
Ahora vamos a usar la librería matplotlib para añadirle algunos elementos a un gráfico como son el titulo, etiquetas del Eje X, del Eje Y, leyendas.
Para ello cargamos a memoria la libreria de matplotlib. Ya lo hemos cargado pero por si no lo hubiera cargado
>>>import matplotlib.pyplot as plt
Para esto vamos a definir tres nuevas series de datos correspondientes las tasas de inflación y ahorro mensuaes y el precio del barril de petróleo, en cientos:
- Tasa de inflación mensual en Lima en un período de Junio 2018 hasta Mayo 2019: tInfMens
- Tasa anual de ahorro mensual: tAhAn
- Precio del barril de petróleo en los mismos períodos. Para visualizar los tres gráficos, esta variable estará en cientos: cpBpetM.
- Los valores para el eje X: ejeX
Estas son las listas
>>>ejeX = ["Jn18","Ju18","Ag18","Se18","Oc18","No18","Di18","En19","Fe19","Mr19","Ab19","Ma19"]
>>>tInfMens = [0.33, 0.38, 0.13, 0.19, 0.08, 0.12, 0.18, 0.07, 0.13, 0.73, 0.20, 0.15]
>>>tAhAn = [0.70, 0.77, 0.79, 0.80, 0.85, 0.84, 0.81, 0.82, 0.85, 0.85, 0.89, 0.87]
>>>cpBpetM = [0.7415, 0.6988, 0.6984, 0.7325, 0.670, 0.5078, 0.4581, 0.5379, 0.5722, 0.6014, 0.6391, 0.5350]
Se puede comprobar su longitud digitando len(...) nombre de cada variable.
Ahora la gráfica
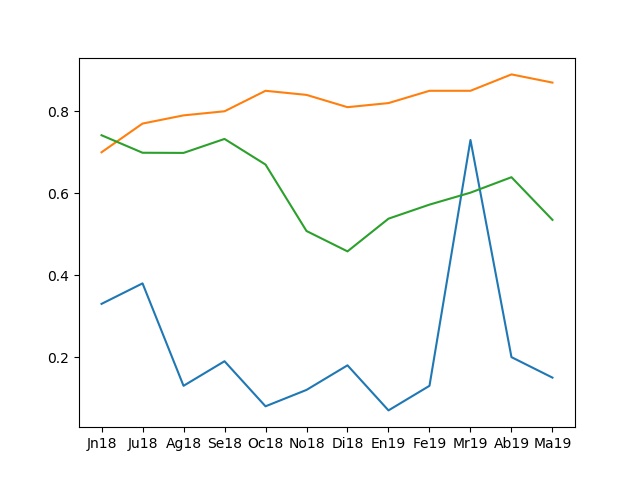
>>>plt.plot(ejeX,tInfMens,ejeX,tAhAn,ejeX,cpBpetM)
>>>plt.show()
La siguiente imagen acompaña a este instrucción
Para completar los elementos del gráfico, haremos uso de las funciones incluidas en la librería matplotlib.pylab, cargada para ser usado por su alias que es plt
Para activar la forma interactiva entre la consola y la ventana de gráfico:
>>>plt.ion()
Para insertar título principal:
>>>plt.suptitle("Grafico")
Para el segundo título
>>>plt.title("Tasa de inflación, ahorro y precio del petróleo por mes")
Etiqueta en el Eje X
>>>plt.xlabel("Meses")
Etiqueta en el eje vertical Y
>>>plt.ylabel("En porcentaje")
Ploteando la tasa de inflación mensual con su etiqueta: tInfMens
>>>plt.plot(tInfMens,label = "Tasa inf mens")
Ploteando la tasa anual de ahorro con su etiqueta: tAhAn
>>>plt.plot(tAhAn,label="Tasa An ahorro")
PLoteando el precio del barril del petróleo dividido entre 100, con etiqueta: cpBpetM
>>>plt.plot(cpBpetM,label="Precio barri pet/100")
Pedimos que se incluya la leyenda
>>>plt.legend()
Ahora ya podemos mostrar el gráfico.
>>>plt.show()
La siguiente imagen muestra esta gráfica.
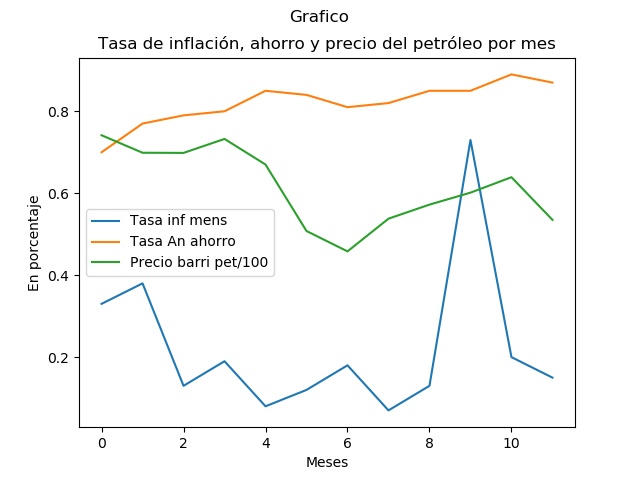
En la siguiente sesión trataremos de hacer algunos gráficos de la Estadística Descriptiva.
Continuar en la siguiente sesión