En la sesión anterior definimos la variable "lista" como una lista de una diversidad de elementos.
Aquí lo tenemos
>>> lista = [1*3,2*4+10,"Luna llena",3**3-15/5,[1,2,3,4,5]]
[3, 18, 'Luna llena', 24.0, [1, 2, 3, 4, 5]]
Este es el caso de una lista elemental y simple:
>>>v = [5,2,8,4,1,4,8,-4]
[5, 2, 8, 4, 1, 4, 8, -4]
Vemos que, como elementos puede tener más de una lista, como el siguiente caso:
>>>x = [[3,5,1,8,4],[2,3,7,2,4],[0.25,10,20,-10,-8.25],[3,6,8,2,6]]
>>>x [[3, 5, 1, 8, 4], [2, 3, 7, 2, 4], [0.25, 10, 20, -10, -8.25], [3, 6, 8, 2, 6]]
En efecto, x se ha convertido en una lista de listas; más todavía, si cada lista se convierte en fila, podemos pensar en una matrzi (4x5).
De todo esto podemos deducir que una lista es, simplemente un arreglo ordenado de elementos cada uno de los cuales están definidos por la posición que ocupan en la lista.
Y ocurre que es esta la definición de un vector o matriz, en los ámbitos de la matemática. Con una sola condición: Que sus elementos sean valores numéricos.
En consecuencia, todas las listas numéricas como "v", pueden constituir vectores y, por tanto, podemos estar hablando de desarrollar todo un capítulo de vectores.
Del mismo modo, todas las listas numéricas como el caso de x, pueden constituir matrices y, por tanto podemos estar hablando de desarrollar todo el álgebra lineal, habiendo empezado con listas.
Pero ya hemos visto que, si
>>>w = [3,6,7,4,-5,1,6,2]
No tiene sentido la suma, el producto ni el producto de un vector por un escalar, como podemos verlo de nuevo aquí.
>>>v+w [5, 2, 8, 4, 1, 4, 8, -4, 3, 6, 7, 4, -5, 1, 6, 2]
>>>v*w
>>>3*v
[5, 2, 8, 4, 1, 4, 8, -4, 5, 2, 8, 4, 1, 4, 8, -4, 5, 2, 8, 4, 1, 4, 8, -4]
¿Qué es lo que falta?
Usar otras librería propiadas para el tema: La librería numpy
Al Python le asisten muchas y diversas librerías definidas en términos de módulos. Estos módulos contienen muchas y en algunos, muchísimas funciones orientadas a asistirnos en nuestras dificultades, enriqueciendo al Python.
Para usar una de estas librerías debemos importarlas hacia el Python usando: import numpy en el IDLE de Python o en el CMD
>>>import numpy
>>>
Ahora, para usar la funciones contenidas en esta librería, debemos usar uno de los siguientes formatos:
>>>numpy.funcion(...) o
>>>variable = numpy.funcion(...)
La manera de crear un vector o matriz, a partir de una lista, es usar la función array(...) usando el formato: numpy.array(...).
Lo primero que haremos es convertir a las lista v y w en arreglos vectoriales y los dejaremos en los mismos nombres
>>>v=numpy.array(v)
>>>v
array([ 5, 2, 8, 4, 1, 4, 8, -4])
>>>w = numpy.array(w)
>>>w
array([ 3, 6, 7, 4, -5, 1, 6, 2])
Puesto que cada vez que usemos alguna función de numpy debemos anteponerla a la función, reduzcamos la dificultad denominando al módulo mediante un "alias".
>>>import numpy as np
De esta forma ya no usaremos "numpy." sino "np."
Ejemplo 1
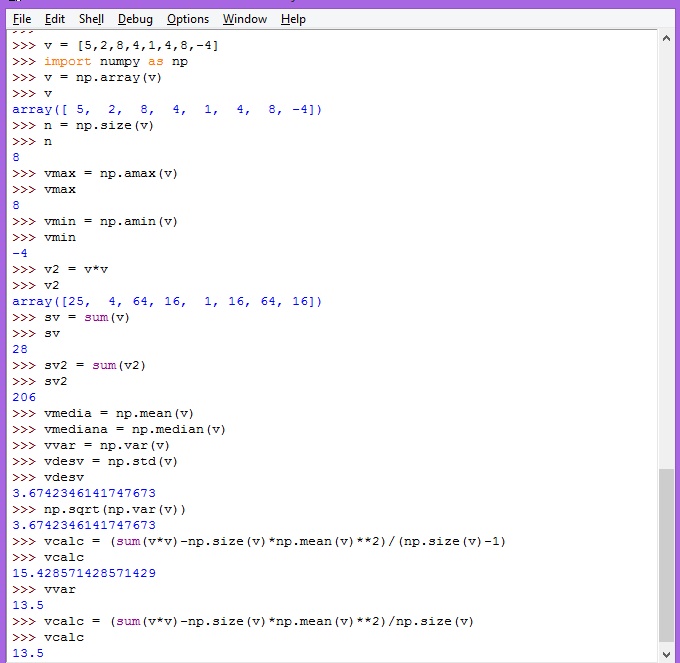
Vamos a realizar algunas operaciones con la lista v, convertida en un arreglo vecorial. Empecemos desde cero
>- Definimos la lista v = [5,2,8,4,1,4,8,-4]
- Importamos la librería numpy y la denominamos np
- Convertimos en vector con el mismo nombre a la lista v, usando np.array(v)
- Obtenemos el tamaño de este vector usando np.size(v) y dejamos en n
- Determinamos el máximo elemento en v, usando np.amax(v) y lo dejamos en vmax
- Hacemos lo mismo el mínimo dejándolo en vmin
- Dejamos en v2 el producto de v*v (sus elementos estarán al cuadrado) usando v*v
- Dejamos en sv la suma de los elementos de v, usando np.sum(v)
- Dejamos en sv2 la suma de los cuadrdo de v, usando np.sum(v2)
- Obtenemos la media y la dejamos en vmedia, usando np.mean(v)
- Obtenemos la mediana y la dejamos en vmediana, usando np.median(v)
- Obtenemos la varianza de v, dejándolo en vvar, usando np.var(v)
- Obtenemos la deviación estándar de v y la dejamos en vdesv, usando np.std(v)
- Calculamoa la raiz cuadrada de la varianza para saber si es cierto que np.std nos devuelve la desviación estándar, usando np.sqrt(np.var(v))
- Finalmente nos atrevemos a calcular la varianza de v usando la fórmula que se indica en la siguiente imagen.
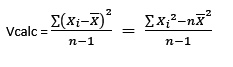
Podemos comprobar que la varianza que calcula Python es, dividiendo a la suma de los desvíos cuadráticos por n y no por n-1 que es la fórmula para muestras.
La siguiente imagen muestra todo este trabajo realizado sobre un vector
En la siguiente sesión haremos una aplicación y continuaremos con vectores pero trabajando con varios vectores.