En Python los tipos de datos numéricos básico son:
- Los enteros int(), que no toman en cuenta la parte decimal
- Los reales de coma flotante float(), que consideran la parte decimal
- Los complejos, compuestos por una parte real y otra imaginaria, cuyo formato es a+bi
Ya hemos hecho algunos ejmplos con enteros y reales(flotantes). Veamos algunos ejemplos con los datos numéricos complejos.
La estructura de un número complejo es: a + bi o visto como par ordenado (a,b), donde la primera componente representa la parte real del número y la segunda, la parte imaginaria, la cual está acompañada por el símbolo i. Siendo j = √-1
Ejemplo 1
Si queremos la forma compleja de (4,5)
>>>complex(4,5)
(4+5j)
>>>x = complex(-8,10)
>>>x (-8+10j)
>>>y = complex(-12,25i)
>>>z = complex(12.5,20.12)
>>>z (12.5+20.12j)
Operaciones aritméticas con números complejos:
La suma
>>>s = x+y
>>>s
(-20+35j)
>>>x+y-z
(-32.5+14.879999999999999j)
La diferencia:
>>>r = x-y
>>>r
(4-15j)
El producto
>>>p=x*y
>>>p
(-154-320j)
¿Cómo así?: (-8+10j)x(-12+25j) = (96-200j-120j+(10√-1 x 25√-1)) = (96-320j-250) = (-154+320j)
Python, siendo un producto de los sistemas abiertos, cuenta con una cantidad muy grande de librerías tanto los que conforman la estructura de Python como aquellas que incrementan su potencia.
Las librerías referidas a los datos numérico tenemos al módulo math y mathc
Para disponer de esas librerías, debemos importarlas usando uno de las siguientes sentencias import:
>>>import math
>>>from math import log
>>>import math as M
>>>from math import *
La primera y última orden son iguales
La segunda importa el módulo que posee la función log
Y la tercera importa la librería math pero al referirnos a ella usaremos M en lugar de math
Los módulos contenidos en esta librería son muchos, algunos de los cuales los usaremos ahora.
Nota
Al digitar math. y esperar uno o dos segundos, vera un menú contextual mostrando una lista de todas las funciones contenidas en este módulo. Puede seleccionar de esta lista usando la tecla [tab] o [Intro]
La función:
- math.ceil(...), devuelve el próximo entero mayor o igual que el argumento
- math.floor(...), devuelve el próximo entero menor o igual que el argumento
- math.pi, devuelve el valor de pi
- math.fmod(a,b), devuelve el resíduo de la división de a entre b
- math.gcd(a,b,c,...), devuelve el MCD de los elementos que figuran como argumentos
- math.pow(a,b), devuelve el resultado de ab
- math.sqrt(...), devuelve la raíz cuadrada del argumento.
- math.radians(...), devuelve la conversión del argumento a radianes
- factorial(...) devuelve el factorial del argumento
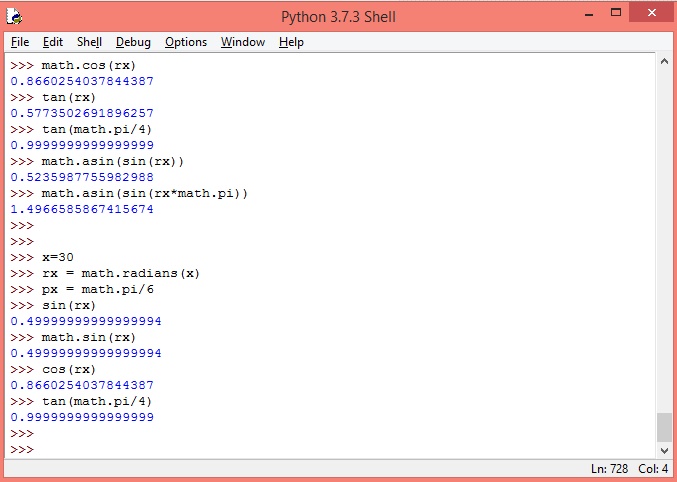
La siguiente imagen muestra el uso de las funciones matemáticas

Entre las funciones exponenciales y logarítmicas, tenemos:
- math.exp(1), devuelve el valor de e1
Lo comprobamos con >>>exp(1)que se encuentra en la librería estándar de Python
-math.e, devuelve el mismo valor que math.exp(1) o exp(1)
- math.log(x[,base]), devuelve el logaritmo de x, en la base "base". Puesto que es opcional, si no se usa devuelve el logaritmo de base "e"
- math.log(20,2), devuelve el logaritmo de 20 en la base 2
Lo podemos comprobar usando la definición: log(a,b) = log(a,e)/log(b,e) = log(a)/log(b)
- math.log10(...), devuelve el logaritmo decimal del argumento. El mismo resultado se obtiene usando la librería del Python: log(100,10) o log10(100)
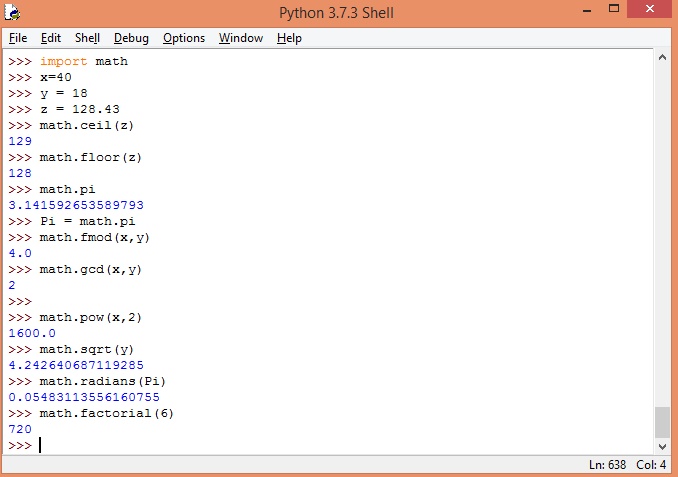
La siguiente imagen muestra el uso de las funciones
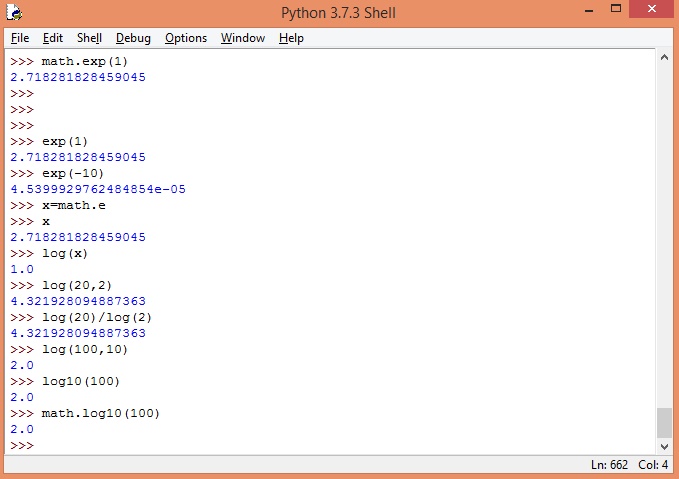
Entre algunas de las funciones trigonométricas tenemos:
- math.sin(...), devuelve el seno del argumento. El argumento debe estar en radianes
- sin(...), como el caso anterior, devuelve el seno del argumento. Esta es una función de la librería estándar de Python
- math.cos(...), devuelve el coseno del argumento.
- math.tan(...), devuelve la tangente del argumento.
- math.asin(...), devuelve el arco coseno del argumento.
La siguiente imagen muestra algunas operacione con esta funciones