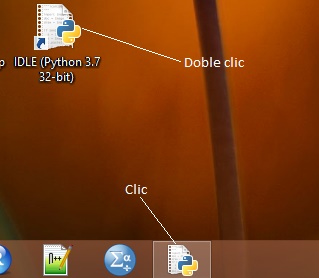
Empecemos a usar el Python.
ahaga clic según corresponda, según la siguiente imagen, para cargar a memoria el Python.

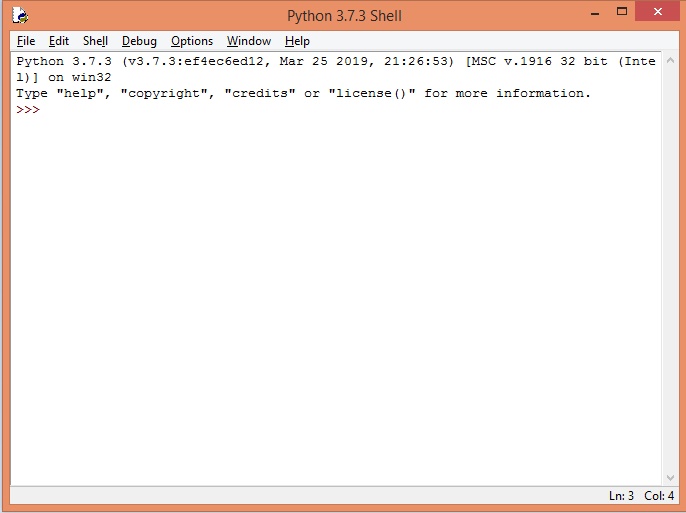
Al ejecutar el IDLE de Python, obtendrá la siguiente ventana:
Sin embargo, si hubiéramos ejecutado el Python 3.7, que es el otro programa ejecutable de acceso directo alojado en la carpeta de instalación,
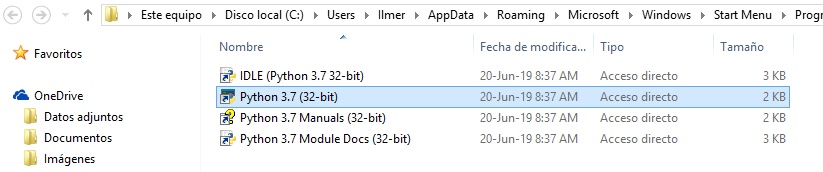
habríamos obtenido la siguiente ventana:

Como puede apreciar, en ambas ventanas, la última línea muestra ">>>" que es el símbolo o "propmp" que indica que el Python está listo para recibir nuestras órdenes.
A partir de este punto ya podemos usar la ventana para procesar las maravillas de este lenguaje.
¿En qué se diferencian estas dos formas de consola o terminal?
La ventana en negro es la ventana del CMD del Windows. En ella se digitan los comandos del Python como si fueran los comandos del DOS antiguo, previo al lanzamiento del WIndows 1.0
No está mal usarla. Pero la otra ventana, propia del IDLE de Python, es más completa en el sentido de que podemos usar su barra de menú que amplía el uso del Python más allá de una simple calculadora.
Sin embargo, la ventana del CMD DOS nos servirá en algunos casos como cuando se deba instalar algunos módulos para los cuales se requiere del uso del comando PIP ...Dejaremos de pensar en esa ventana cuando instalemos el "Visual Studio Code.
Bien, empecemos entonces.
Python usado como una calculadora básica, en modo interactivo
Acuérdese de su infaltable calculadora y simulemos estar con ella de forma que podemos sumar "+", restar "-", multiplicar "*", dividir "/", elevar a una potencia: "**":
Después del prompt ">>>", digite: >>>5*8 y presione [Intro]. Cada vez que quiera ingresar la petición, debe presonar [Intro]
En la siguiente línea se visualizará 40 como respuesta.
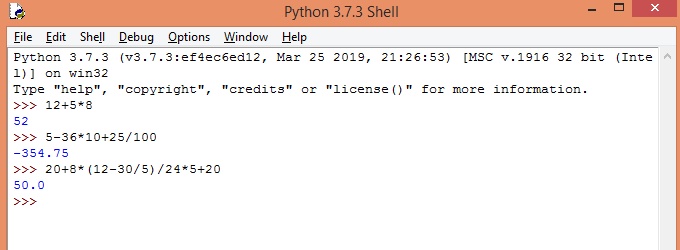
He aquí algunas cálculos que podemos hacer:
Antes de explicar cómo lo ha hecho, veamos el orden de prioridad de los operadores aritméticos.
| ¿En qué orden se ejecutan los operadoresaritméticos? | ||
| Primero | Dentro de los paréntesis | (...) |
| Segundo | Las potencias | ** |
| Tercero | La división y multiplicación | /, *, //, % |
| Cuarto | La suma y resta | +, - |
| Quinto | Operadores relacionales | ==,!=, <, >, <=, >= |
Expliquemos cómo se ejecutan las tres líneas de ejemplo:
En la primera: 12+40. Resultado: 52
En la segunda: 5-360+25/100 ---> 5-360+0.25 ---> -354.75
En la tercera: 20+8*(12-6)/24*5+20 ---> 20+8*6/24 ---> 20+48/24*5+20 ---> 20+2*5+20 ---> 20+10+20 --->30+20 ---> 50.0. Lo convierte a decimal por la división.
También podemos ingresar texto y ver el resultado. La siguiente imagen muestra lo que sucede si ingresan diferentes formas de texto

Como vemos, el texto debe estar encerrado entre doble o simple comillado
A todo texto le llamaremos cadena de caracteres.
No se puede puede pretender ingresar una cadena unido a un valor numérico
Si la expresión matemática está encerrada en comillas dobles o simples, se toma como una cadena de caracteres y no una expresión numérica.
Las cadenas, aunque contengan sólo números, no siendo expresión numérica, no se ejecutan.
Continuando con los ejemplos, supongamos que tenemos la siguiente expresión numérica: 32+5*12/(8+250.5)
La expresión que debemos ingresar en la consola es: >>>3**2+5*12/(8+25**0.5) El resultado será 13.615384615384615
El resultado de >>> 25+37//4 será 34
El resultado de >>> 25+37//4-18%7 será 30
como se muestra en la siguiente imagen

En la primera expresión: 9+5*12/(8+5) ---> 9+5*12/13 ---> 9+60/13 ---> 9+4.615384615384615 ---> 13.615384615384615
El operador "//" devuelve el cociente entre dos número truncando la parte decimal, si tuviera. En el caso de 37//4 devuelve 9.
El operador "%" devuelve el residuo de la división de dos número. En el caso de 18%7 devuelve 4.
Dada la ecuacción cuadrática: 3x2-5x+18. Una de las raíces será:
>>>(5+(5**2-4*(-3)*18)**0.5)/(2*3)
La otra raíz la calcularemos con la siguiente expresión:
>>>(5-(5**2-4*(-3)*18)**0.5)/(2*3)
Esto se muestra en la siguiente imagen:

En el caso de la segunda raíz, las operaciones se realizarán de la siguiente manera:
(5-(25-4*(-3)*18)**0.5)/6 ---> (5-(25+12*18)**0.5)/6 ---> (5-241**0.5)/6 ---> (5-15.52417469626)/6) --> -10.52417469626/6 ---> -1.75402911604334
En cuanto a cadenas, la única operación que podríamos hacer es la "suma":
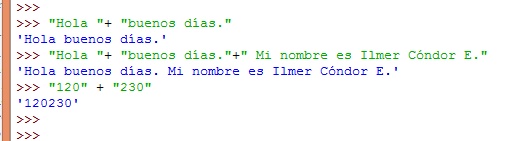
Esta operación de añadir las cadenas, es lo que se llama concatenación.
Ahora bien, en una calculadora, tenemos la capacidad de almacenar datos numéricos o resultados de operaciones previas en la "memoria" para luego invocarlas y usar lo que está almacenado en ellas.
¿Se puede hacer esto en Python?
Por supuesto que sí. Para ello se requiere de variables que serán las "memorias" donde podremos guardar el dato o resultado.
Esto lo veremos en la siguiente sesión.